接触式传感器测量软体驱动器角度的数据融合

刘艳红，豆园林，任海川，曹桂州

（郑州大学 电气工程学院，郑州 450001）

0 概述

采用软材料或柔性材料加工的软体机器人对非结构化的环境有很好的适应性和人机交互的安全性［1］。软体机器人相较于传统的刚性结构具有高灵活性、复杂环境适应性和人机交互安全性的优势，在医疗康复、勘测救援等领域具有广阔的应用前景。软体驱动器是软体机器人动力组成部分，实现软体机器人的广泛应用不能缺少对软体驱动器形状信息的检测，准确测量软体驱动器角度有利于软体机器人实现形状重构、闭环位置控制和姿态实时监测。然而，由于软体驱动器本身具有高度柔顺性，传统的传感器很难应用到软体驱动器角度测量上［2］。因此，如何准确获取软体驱动器形状反馈信息（如角度变化）是软体机器人研究的挑战性问题之一。

基于视觉传感器［3-4］的测量方法被广泛应用于软体驱动器角度测量，但其易受外界环境光线、障碍物遮挡、工作区域等因素的影响。因此，一些学者从不同的测量原理出发，设计了多种用于测量软体驱动器角度的非视觉传感器，包括电阻式传感器［5-6］、光学传感器［7-8］和电磁式传感器［9］。由于制作简单、造价低、柔韧性好、对磁场不敏感等特性，电阻式传感器已经在商用数据手套中成功应用［10］。为了使传感装置更易植入软体驱动器中，文献［6］以银浆作为敏感元件，采用3D 打印自制曲率传感器。虽然具有制造简单、造价低等特点，但自制的传感器仍存在迟滞和漂移效应，限制了传感器测量的精度。相较于电阻式传感器，电磁式传感器具有高测量精度和灵敏度的特点。文献［9］将线性霍尔元件和磁铁嵌入到软体手臂中，以软体手臂弯曲时的高度变化反映软体手臂弯曲的角度变化，实现在形状记忆合金驱动下软体手臂的角度测量。然而，外界磁场的变化将直接对敏感元件带来干扰，影响测量的准确性［11］。光纤传感器［8］免除了电阻式传感器以及电磁式传感器的测量缺陷，通过检测光纤传感器光强的变化实现软体驱动器姿态传感检测，但光纤传感器复杂昂贵的制造工艺、额外的硬件设备和复杂的信号调理电子器件限制了光纤传感器模块化集成，尚未实现商业化［12］。惯性传感器（Intertial Measurement Unit，IMU）［13-14］具有精度高、质量轻、体积小、造价低、易于实现和可重复性高等优点，常被用于角度测量。文献［15］采用IMU和液态金属混合测量的方式使角度测量精度均方根误差达到3.1°，但腔道变形达到极限时会导致内部液体泄露，惯性传感器的刚性结构在软体驱动器的角度测量中也易受到气道膨胀的影响。综上所述，针对软体驱动器角度测量，目前仍缺少高精度、高可靠性、造价低且易制造的接触式传感器。

为提高软体驱动器角度的测量精度，可利用高清摄像头测量软体驱动器标记点来计算软体驱动器的角度作为角度测量基准，选择质量轻、造价低的商用曲率传感器和九轴姿态传感器，采用数据融合算法［16-17］实现软体驱动器角度的测量。九轴姿态传感器测量软体驱动器末端姿态角度的精度易受软体驱动器气道膨胀的影响，内部集成的陀螺仪角速度估计软体驱动器角度也容易产生累计误差。采用卡尔曼滤波算法融合惯性传感器和曲率传感器角度测量数据，可有效减少接触式传感器受气道膨胀的影响。然而，曲率传感器测量软体驱动器角度容易受到漂移影响，造成卡尔曼滤波算法融合曲率传感器与惯性传感器精度有限。

本文采用模糊推理与卡尔曼滤波结合的数据融合算法融合曲率传感器和九轴姿态传感器数据，减少接触式传感器受漂移、气道膨胀的影响。同时利用长短时记忆（Long Short-Term Memory，LSTM）网络、BP 神经网络分别融合接触式传感器角度测量值，给出角度测量的优化融合方案。

1 测量系统整体设计和实验步骤

本文采用jy901 九轴姿态传感器和flex 4.5 寸曲率传感器对软体驱动器的角度进行测量。jy901 传感器内部集成了高精度的陀螺仪、加速度计和地磁场传感器。姿态角度测量稳定性达到0.01°，角速度测量稳定性达到0.05°/s。flex 曲率传感器阻值变化范围：180°捏弯的阻值是未被弯曲电阻的2倍。数据融合方案如图1所示。其中：低通滤波器对曲率传感器测量值进行滤波，得到弯曲角度；九轴姿态传感器分别输出软体驱动器末端部位的翻滚角度和翻滚角速度，并利用角速度与时间的乘积估计软体驱动器角度；长短时记忆网络和BP 神经网络分别融合曲率传感器测量角度和九轴姿态传感器翻滚角度；模糊推理算法推断九轴姿态传感器受气道膨胀影响下的翻滚角膨胀量，并取代静态下曲率传感器角度测量值，以减少曲率传感器漂移效应，卡尔曼滤波算法融合九轴姿态传感器角速度积分值与模糊推理下的曲率传感器角度测量值，最终计算得到4 个角度的融合值。

图1 传感器融合方案Fig.1 Sensor fusion scheme

实验平台由固定装置、传感器、控制盒、软体驱动器以及笔记本电脑组成。固定装置由铝型材搭建成的300 mm×300 mm×260 mm 长方体骨架，用于固定各传感器以及软体驱动器。控制盒由STM32F103开发板、导气管道、气压传感器、电磁阀与调节阀组成。各传感器安装位置以及软体驱动器弯曲角度示意图如图2 所示。其中：flex 4.5 寸曲率传感器安装在软体驱动器弯曲侧；jy901 九轴姿态传感器安装在软体驱动器末端位置；高清摄像头固定在软体驱动器前方。

图2 传感器安装和软体驱动器弯曲角度示意图Fig.2 Schematic diagram of sensor installation and soft actuator bending angle

视觉传感器获取软体驱动器弯曲图像，采样频率达到30 HZ，角度测量精度达到0.2°；九轴姿态传感器最高采样频率为200 HZ，姿态角度测量精度静态0.05°，动态0.1°；九轴姿态传感器末端位置属于软体驱动器可延展层，而气道膨胀会造成九轴姿态传感器测量软体驱动器姿态角精度下降。曲率传感器与九轴传感器同频输出，角度测量精度达到4.5°。假设软体驱动器在有气体通过的部分为圆弧弯曲，r表示圆弧弯曲半径，m表示圆弧弦长。采用MATLAB 的OpenCV 工具箱识别图像中黑色标记点的位置信息，如图2 右上角所示，软体驱动器在x轴和y轴组成的平面内做弯曲运动，两圆形标记点组成的长度为m向量与y轴夹角θ的2 倍，即为软体驱动器的角度变化值。

实验采用气泵作为动力源，设置气压在37～55 kPa范围，通过对软体驱动器的多周期充放气，实现基于各传感器的角度测量实验。首先，气源通过电磁阀和气缸对软体驱动器进行恒压驱动，时间是20 s；然后，关闭气源电磁阀并打开放气电磁阀，时间是20 s。在相同气压下，需要重复采样3 次，测试高清摄像头重复采样精度，采样时间为0.08 s。实验共采集180 个周期的软体驱动器弯曲角度数据，每个周期为40 s，共获得89 900 个采样点。每个样本点数据包括九轴姿态传感器翻滚角度、陀螺仪X轴角速度、曲率传感器测量值、软体驱动器气压值。采用均方根误差和标准均方根误差作为评价指标，比较传感器及数据融合算法的精度，如式（1）和式（2）所示。

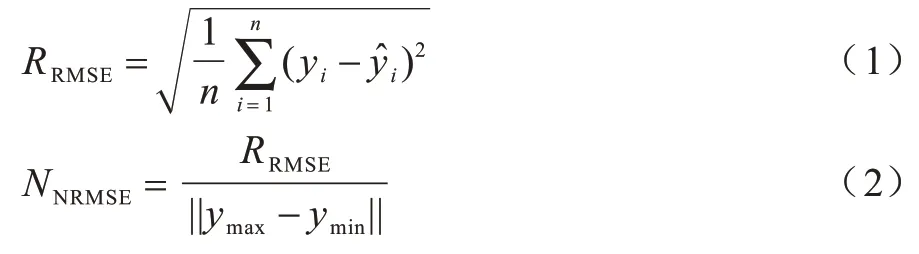
其中：yi表示模型值表示测量值；||ymax-ymin||表示最大角度与最小角度的欧氏距离。

2 数据融合算法

常用的数据融合算法有人工神经网络［18］、深度学习网络［19-20］、卡尔曼滤波［21-22］、加权平均、D-S 证据推理［23］、模糊推理等。卡尔曼滤波通过模型和传感器测量值估计最优状态，被广泛应用于多传感器数据融合。人工神经网络如BP 神经网络能够学习特征，存储先验知识，通过训练神经网络，可以完成物体模式识别（如人体运动识别）、数据分类和预测功能。深度学习网络如长短时记忆网络（LSTM）可以更好地解决时间序列问题，训练长时间滞后数据。模糊推理根据模糊集合理论，可以较好地对模糊不明确信息进行判断。

2.1 BP 神经网络

神经网络是一种按照误差逆向传播算法训练的多层神经网络。传统的BP 神经网络结构由输入层、隐层和输出层组成，每层包含数个节点。基于神经网络能够融合特征实现数据的预测对传感器信息进行数据融合。隐层神经元个数的选取可以根据式（3）确定。

其中：m表示隐层神经元的个数；p表示输入层的个数；o表示输出层的个数；∂是1～10 之间的常数。采用MATLAB 2018a 深度学习工具箱中的神经网络函数创建BP 神经网络。BP 神经网络输入层为2，分别为jy901 传感器翻滚角以及flex 传感器角度值。最大迭代次数分3 种情况（600、900、1 200），隐层分3 种情况（3、8、13），输出层为1，学习率为0.000 2。此外，BP 网络将测量的总数据按8∶2 比例分为训练数据集和预测数据集。

2.2 长短时记忆网络

LSTM 网络相比于BP 神经网络可以从训练数据中模拟出更复杂的结构。LSTM 可以更好地解决时间序列问题，能够记忆长时间的历史数据。LSTM有很多记忆块，每个记忆块由输入门、记忆细胞、遗忘门和输出门组成。每个记忆块运行原理如下：

1）数据通过遗忘门从细胞状态丢弃某些信息。

遗忘门采用σ函数，根据之前记忆块输出值ht-1与当前输入值xt生成0～1 的ft函数值给每个细胞状态Ct-1，1 表示之前的记忆通过，0 表示之前的记忆舍弃。ft函数的表达式为：

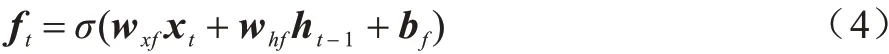
2）决定新信息将被存储在细胞状态中。

这一步分成两部分：首先输入门将决定某些值会被更新，然后记忆门将会形成一个新的候选值Ct添加到细胞状态中，根据以下方式更新状态：

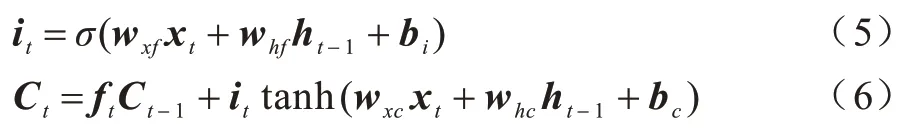
3）由输出门决定信息的输出。

式（7）所示的σ函数决定输出细胞状态某一部分。在此基础上，式（8）通过tanh 函数将Ct值调整为-1 到1，并将其乘以sigmoid 门的输出，以便只输出目标信息。

在式（4）～式（8）中：f、i、C、o、h分别表示遗忘门、输入门、细胞状态、输出门和隐层输出；Wx和Wh输入和隐层权值；b表示偏移量；σ函数表示sigmoid 激活函数。

实验设置LSTM 输入层数为2，与BP 神经网络输入数据保持一致，输出层数为1，求解器设置为‘adam’，最大迭代次数分3 种情况（600、900、1 200），隐层神经元分3 种情况（100、150、200），减少神经网络融合结果的偶然性，提高LSTM 融合结果的可信度。硬件使用GPU 进行训练。LSTM 神经网络初始学习率设置为0.005，学习率下降周期为200，学习率下降因子为0.2，LSTM 网络将测量的总数据按8∶2比例分为训练数据集和预测数据集。

2.3 卡尔曼滤波

卡尔曼滤波是一种高效的递归滤波器，能够实现系统状态的最优估计。本文选用卡尔曼滤波融合曲率传感器和九轴姿态传感器。卡尔曼滤波选用式（9）和式（10）所示的形式。

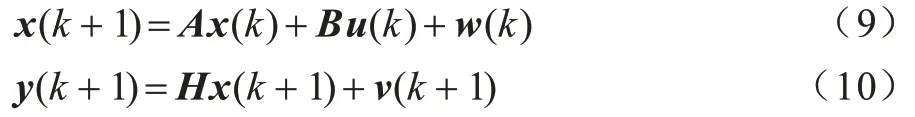
其中：w(k) 和v(k+1)表示过程噪声和测量噪声；y(k+1)表示k+1 时刻测量变量；H=1 表示测量矩阵；A=1 为系统矩阵；B=1 为输入矩阵表示k时刻陀螺仪角速度；t为采样周期。测量矩阵以及状态矩阵分别如式（11）和式（12）所示。

其中：fflex(k)为k时刻曲率传感器测量值；θ(k)表示k时刻软体驱动器弯曲角度。卡尔曼滤波通过式（13）～式（17）方程完成状态的最优估计。

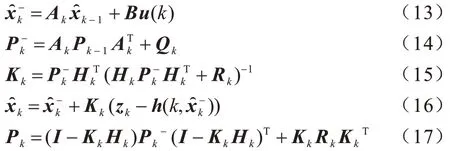
其中：Qk和Rk分别表示过程激励噪声协方差矩阵和测量噪声协方差矩阵；Pk表示k时刻状态协方差矩阵。

2.4 模糊推理

模糊推理是采用模糊逻辑由给定的输入到输出的映射过程。模糊推理包括输入变量模糊化、在模糊规则前件中应用模糊算子、根据模糊蕴含运算由前提推断结论、模糊合成、输出变量反模糊化5 个过程。模糊规则主要以“if …，then”的形式，其中，“if”部分通常称为模糊规则的前件，“then”称为模糊规则的后件。根据模糊蕴含运算由前提推断结论，即规则“if x is A，then y is B”，记为A→B。

定义翻滚角的论域为［0°180°］，模糊子集为：｛XA，JX，ZA，JD，DA｝=｛小角度，较小角度，中角度，较大角度，大角度｝；气道膨胀量模糊输出的论域［－20°0］，模糊子集为：｛XF，JXF，ZF，JDF，DF｝=｛小负，较小负，中负，较大负，大负｝。模糊规则的制定：

1）如果翻滚角为XA，则输出为XF；

2）如果翻滚角为JX，则输出为JXF；

3）如果翻滚角为ZA，则输出为ZF；

4）如果翻滚角为JD，则输出为JDF；

5）如果翻滚角为DA，则输出为DF。

3 实验与结果分析

基于上述实验过程，本文对高清摄像头采样点进行3 次重复采样数据分析。实验结果表明，每个样本点最大值和最小值之差与样本点平均值的平均误差为0.78%，表明高清摄像头具有较高的重复测量精度，可作为软体驱动器角度测量的基准。

最大迭代次数以及隐层节点数都会对神经网络融合结果造成影响。针对不同的融合对象，最大迭代次数和隐层节点数并没有唯一公式可以确定。因此，对于神经网络融合曲率传感器和惯性传感器，研究确定神经网络最大迭代次数和隐层节点数对于融合惯性传感器和曲率传感器具有重要研究意义。采用LSTM 神经网络和BP 神经网络进行数据分析，3 种最大迭代次数预测结果如表1 所示，其中，RL_RMSE表示LSTM 融合结果均方根误差，RB_RMSE表示BP 神经网络融合结果均方根误差。

表1 LSTM 和BP 网络不同迭代次数均方根误差比较Table 1 Comparison of root mean square error of different iterations between LSTM and BP network (°)

由表1 可知，神经网络不同的迭代次数对接触式传感器数据融合影响较大。对比表1 融合结果，当BP 神经网络和LSTM 网络最大迭代次数为1 200时，融合flex 曲率传感器和惯性传感器精度最高。故将两种神经网络的迭代次数选为1 200。测试隐层节点参数对BP 神经网络和LSTM 网络融合结果的影响，均方根误差结果如表2 和表3 所示。

表2 BP 神经网络不同隐层节点下均方根误差Table 2 Root mean square error of different hidden layer nodes in BP neural network (°)

表3 LSTM 网络不同隐层节点下均方根误差Table 3 Root mean square error of different hidden layer nodes in LSTM network (°)

由表2 可知，隐层节点数对BP 神经网络融合曲率传感器和惯性传感器结果影响较小，并且过多的隐层节点数会增加网络结构的复杂性，使网络的学习速度下降，容易产生“过拟合”现象。因此，隐层节点根据式（3）、表2 的数据融合结果以及以上隐层节点数的分析，选择隐层节点数为8 对于BP 神经网络数据融合结果较好。然而表3 中LSTM 网络不同的隐层神经元数对惯性传感器和曲率传感器融合结果影响较大，合适的隐层神经元个数能够使LSTM 网络获取满意的融合结果。由于较少的隐层节点数会造成LSTM 网络不能具有必要的学习和信息处理能力，过多的隐层节点一方面会造成LSTM 网络在学习过程中更易陷入局部极小点，另一方面会造成LSTM 网络的学习速度变得很慢。考虑到表3 的融合结果以及LSTM 神经网络隐层节点数的分析，对于LSTM 网络融合惯性传感器和曲率传感器，隐层神经元个数选择150 能够获得较为满意的数据融合结果。

基于LSTM 网络、BP 神经网络和模糊推理与卡尔曼滤波的数据融合结果分别如图3～图5 所示（彩色效果见《计算机工程》官网HTML 版），各传感器测量值和数据融合结果均方根误差和标准均方根误差如表4 所示。从实验结果可以看出，采用模糊推理与卡尔曼相结合融合算法相较于卡尔曼滤波融合可以有效提高接触式传感器测量软体驱动器角度的精度，减少接触式传感器测量软体驱动器角度受漂移以及气道膨胀影响。LSTM 网络融合值均方根误差和标准均方根误差最小，表明LSTM 网络相较于BP 神经网络可以更深度模拟2 种接触式传感器特征输入，LSTM 神经网络针对惯性传感器和flex 曲率传感器数据融合结果在整体测量范围内效果最优。

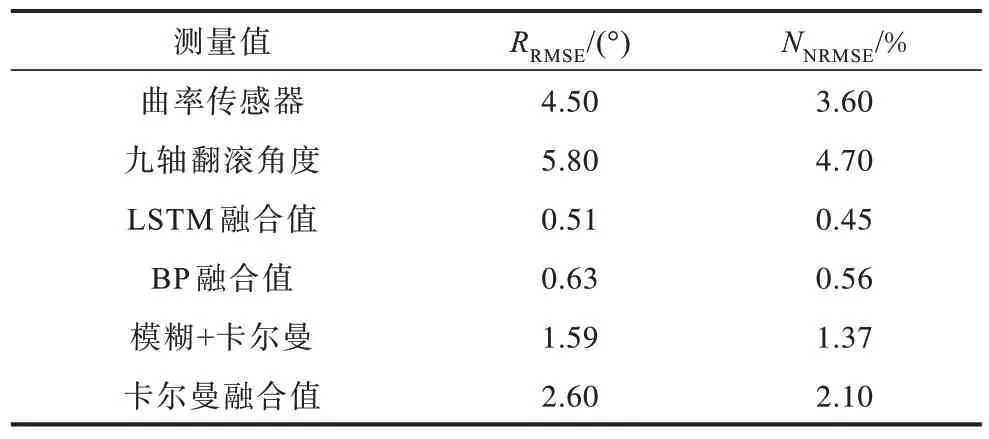
表4 各传感器测量值和数据融合结果Table 4 Measurement value of each sensor and data fusion result

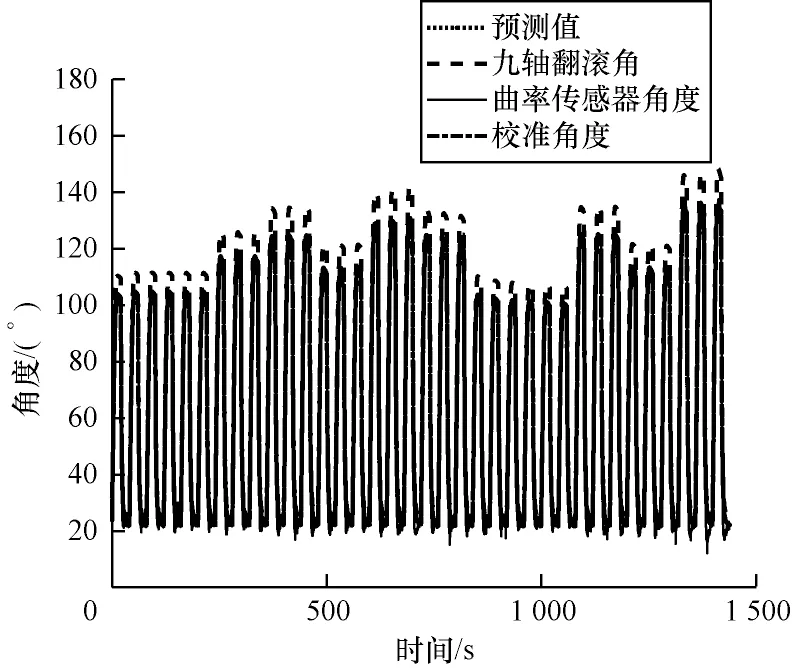
图3 基于LSTM 神经网络的预测结果Fig.3 Prediction results based on LSTM neural network

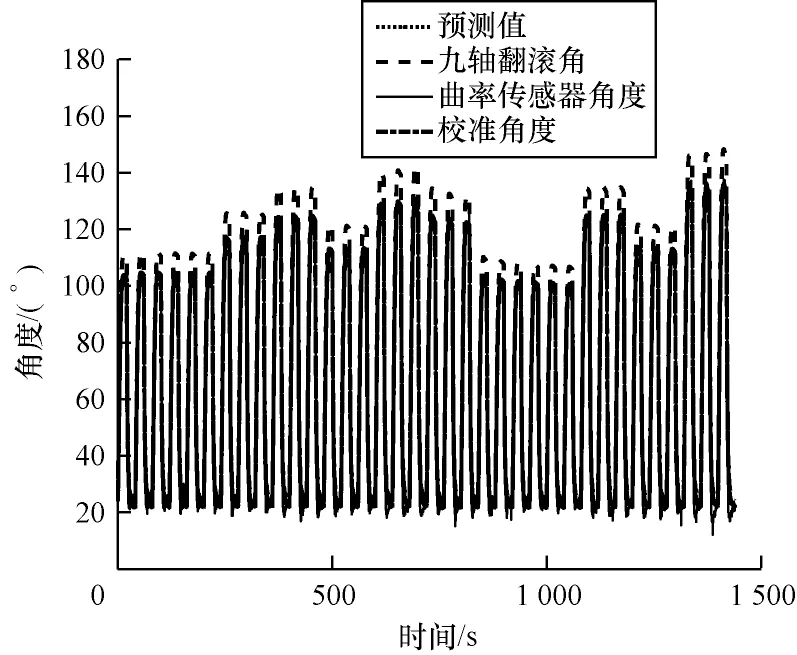
图4 基于BP 神经网络的预测结果Fig.4 Prediction results based on BP neural network

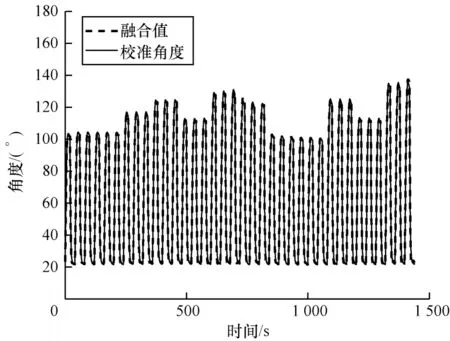
图5 基于模糊推理卡尔曼滤波结合的融合结果Fig.5 Fusion results based on the combination of fuzzy inference and kalman filter

为更进一步比较4 种数据融合算法的局部测量精度，将长短时记忆网络、卡尔曼滤波、模糊推理与卡尔曼、BP 神经网络所有预测结果与视觉传感器测量值之差作绝对值，绝对值越小说明该采样点的局部测量精度最好。对4 种融合算法分别对应的绝对值最小值个数与所有采样点求百分比，得到表5 所示结果。

表5 4 种算法最优融合数据概率分布Table 5 Probability distribution of optimal fusion data of four algorithms %

由表5 可知，模糊推理与卡尔曼相结合的数据融合算法最优概率结果明显优于卡尔曼滤波算法，且概率分布结果与BP 神经网络相近，表明模糊推理与卡尔曼相结合的数据融合算法融合接触式传感器测量软体驱动器角度在局部测量精度上大概率优于单一卡尔曼滤波算法。LSTM 神经网络概率值远大于其他3 种数据融合算法，表明LSTM 神经网络融合结果在局部测量精度大概率要优于其他3 种数据融合算法。

除了分析融合精度，计算速度也是反映数据融合算法的重要指标。本文采用时间消耗对比4 种数据融合算法的计算速度。实验结果表明，平均时间消耗上BP >LSTM >Fuzzy+Kalman >Kalman。BP神经网络平均运行时间最长，卡尔曼滤波算法平均运行时间最短。因此，局部测量精度以及整体测量精度均表明LSTM 神经网络的整体效果远优于其他3 种融合算法，时间消耗也表明LSTM 神经网络要优于BP 神经网络，差于其他两种融合算法。

4 结束语

数据融合模型一般分为基于物理概念的模型和人工智能的模型。对于商用曲率传感器和惯性传感器的数据融合，采用模糊推理与卡尔曼滤波相结合能够有效减少接触式传感器漂移和受气道膨胀影响。然而，基于物理模型的数据融合需要曲率传感器噪声满足高斯白噪声，这限制了数据融合精度。考虑到基于人工智能的模型能够根据曲率传感器和惯性传感器历史数据自主学习模型规律，使人工智能模型在融合复杂数据下具有更好的鲁棒性，本文采用BP 神经网络和LSTM 网络融合2 种传感器的数据规律。实验结果表明，与物理模型相比，人工智能模型能够提高接触式传感器测量软体驱动器角度精度。LSTM 网络相较于BP 神经网络可以更准确地模拟特征的复杂信息，进一步提高角度测量的精度。后续将对视觉传感器和接触式传感器测量软体驱动器角度的数据融合进行研究，以满足软体驱动器在更广泛条件下的应用需求。