基于PCA 与权重贝叶斯的工作面煤与瓦斯突出预测

阎 馨，朱永浩，屠乃威，吴书文，王雨虹

（辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛 125105）

0 概述

煤炭开采时常发生工作面煤和瓦斯突出事故，这对我国经济造成极大损失。采用突出预防方法可以防止事故的发生，其首要工作是突出预测。经过数十年发展，国内外研究者针对事故发生提出多种预测方法，如钻孔涌出初速度方法［1-2］、钻屑指标方法［3-4］、综合指标方法［5］、电磁辐射法［6］、逻辑回归法［7］、神经网络方法［8-10］、支持向量机方法［11-13］、朴素贝叶斯方法［14-15］等。这些方法对工作面突出预测具有一定的积极作用，但存在一些不足，如瓦斯涌出初速度、钻屑量指标、综合指标和电磁辐射监测方法预测时不能综合考虑多种影响因素，因而难以准确确定指标临界值与突出时指标变化趋势的特征。部分指标数据常存在噪声，不能保证突出预测的准确性。神经网络方法考虑工作面煤与瓦斯突出多种影响因素，根据训练样本数据构建预测模型，此模型具有随机性，因此该方法常存在训练失败问题。支持向量机方法适于小规模数据建模，从而构建模型实现突出危险性预测。朴素贝叶斯分类方法将工作面煤与瓦斯突出预测问题归结为分类问题，利用样本数据构建突出预测模型进行突出预测。但该模型在假设模型输入变量（分类变量）间相互独立条件下构建的，而实际构成分类变量的突出影响因素是相互的，因此模型预测的准确性不高。研究发现在朴素贝叶斯模型中考虑分类变量对分类影响的权重，构成权重贝叶斯模型，改进后的模型能有效提高分类的准确性［16-18］。

本文将主成分分析（Principal ComponentAnalysis，PCA）和权重贝叶斯模型结合，构建工作面煤与瓦斯突出预测的权重贝叶斯模型。该模型的预测方法具有较高的预测准确性，可以快速获得突出预测结果。利用主成分分析确定构建突出预测模型输入变量的突出影响因素（分类变量）权重，再构建煤与瓦斯突出预测的权重贝叶斯模型。

1 权重贝叶斯模型构建

1.1 突出预测模型的输入

工作面煤与瓦斯突出是多种因素共同作用的结果。通常情况下，突出危险性与开采深度、瓦斯放散初速度、瓦斯压力呈正相关；与煤层坚固性系数呈负相关。由不同地质构造的煤矿发生工作面煤与瓦斯突出的可能性也不同。其中，高瓦斯煤矿相对于低瓦斯煤矿更易发生工作面煤与瓦斯突出事故。

工作面煤与瓦斯突出预测看作是利用检测到的工作面煤与瓦斯突出多种影响因素信息进行突出危险性等级划分问题。将瓦斯压力、瓦斯放散初速度、地质构造、煤层坚固性系数、开采深度作为工作面煤与瓦斯突出预测分类模型的输入变量，又称分类变量［19］。由于后3 个分类变量是在开采环境发生大变化时才会改变，而且煤层坚固性系数和地质构造信息的检测过程复杂且较长，因此采用离线检测方式获取信息数据。采用多传感器在线检测方式获得瓦斯压力、瓦斯放散初速度信息数据，以提高获取数据的可靠性和准确性。

1.2 突出预测模型

朴素贝叶斯（Naive Bayesian，NBS）模型假设分类变量间相互对立。权重贝叶斯模型是通过对分类变量权重考虑，从而消弱独立性假设条件。如何确定分类变量权重是建立权重贝叶斯模型的关键。常用的权重确定方法有专家给定权重法、层次权重决策法、熵值确定法等。专家给定权重法和层次权重决策法受主观影响较大，有时误差会很大；熵值确定法对于异常数据过于敏感，实际操作时对某些结果影响较小的分类变量权重计算量过大，导致综合权重不切实际。解决不足之处的有效方法是给每个指标增加一个合理范围限制。PCA 是通用的权重确定方法，在多个领域取得较好的应用效果［20-22］，因此应用PCA 对突出预测模型的输入变量（分类变量）进行权重确定。工作面煤与瓦斯突出预测模型建立过程如图1 所示。

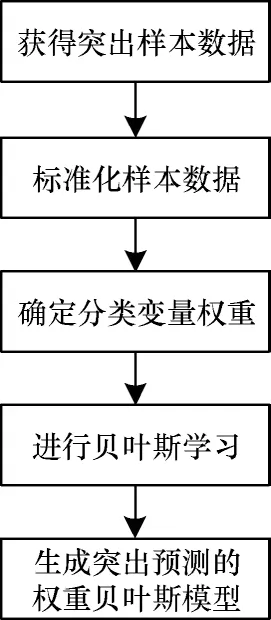
图1 工作面煤与瓦斯突出预测模型建立过程Fig.1 Prediction model building process of coal and gas outburst in mine working

整理瓦斯压力、瓦斯放散初速度、地质构造、煤层坚固性系数、开采深度等信息数据，形成样本数据Xk={xk1，xk2，…，xko}和dk（k=1，2，…，m，o=5，m为样本数）。xk1，xk2，…，xk5分别为第k个样本的5 种分类变量数据，dk为第k个样本的突出危险性等级数据。

对样本数据Xk={xk1，xk2，…，xko}进行Z-Score 标准化处理，处理后的数据Y如式（1）所示：

对标准化处理后的数据Y进行主成分分析，计算出瓦斯压力、瓦斯放散初速度、地质构造、煤层坚固性系数和开采深度作为分类变量时的权重。确定以分类变量权重为基础，利用数据Y进行贝叶斯学习，完成类别的先验概率计算以及获取条件概率公式。利用朴素贝叶斯的学习结果和分类变量权重构建工作面煤与瓦斯突出预测的权重贝叶斯模型。

利用主成分分析，确定分类变量权重过程如下：

步骤1计算数据Y的相关系数矩阵R。R的表达式如式（2）所示：

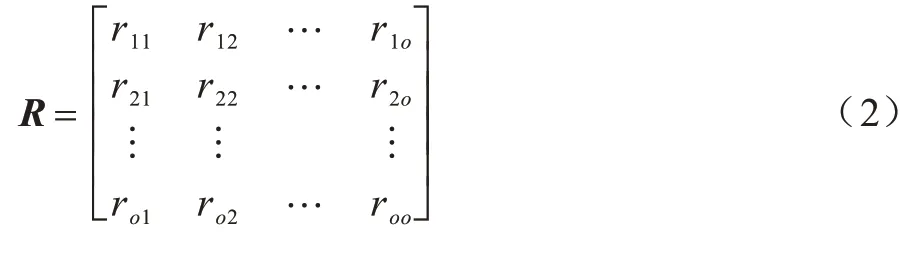
步骤2计算相关系数矩阵R的特征值λi（i=1，2，…，o，λ1≥λ2≥…≥λo）和特征向量μij（i，j=1，2，…，o）。

步骤3根据式（3）确定主成分个数n。

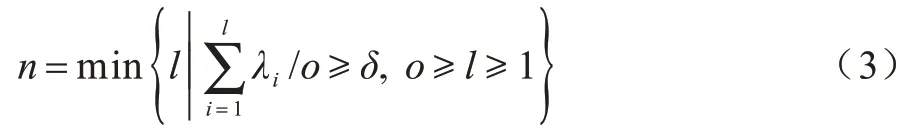
其中，δ为参数，表示主成分贡献率阈值。

步骤4根据式（4）计算主成分因子载荷矩阵βij（βij代表第i个分类变量与第j个主成分间相关系数，i=1，2，…，o，j=1，2，…，n）。

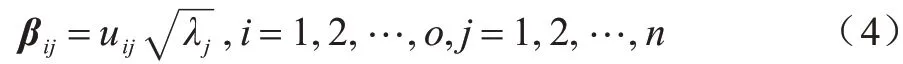
步骤5根据式（5）～式（7）计算得各分类变量的权重θi（i=1，2，…，o）。

由式（5）～式（7）可知，分类变量的权重与相关系数βij密不可分。一类分类变量在一个主成分上的影响权重由式（5）表示，|βij|越大，第i个分类变量与第j个主成分间相关系数越大，第i个分类变量对第j个主成分的影响就越大，即当第i个分类变量发生定量变化，则第j个主成分相应发生变化量越大。将煤与瓦斯突出事故发生时看作是o个分类变量（本文中是5 种分类变量）构成系统相互作用的结果，而n个主成分构成系统是o个分类变量构成系统的另一种表达，因此煤与瓦斯突出发生也是n个主成分构成系统作用的结果。当把在n个主成分上相加得到即一个分类变量对n个主成分构成系统影响的量化，再对进行归一化得到该分类变量权重θi。θi越大，当第i个分类变量发生定量变化，n个主成分构成系统发生变化量越大，对煤与瓦斯突出危险性影响的量化也就越大。

设工作面煤与瓦斯突出危险性等级为B1，B2，…，Bf（f为突出危险性等级数量），在m个样本数据中，突出危险等级为Bl(l=1，2，…，f)的样本数量为Sl(l=1，2，…，f)。为避免出现频率为0 的情况，影响煤与瓦斯突出预测的准确性，引入拉普拉斯平滑计算，Bl(l=1，2，…，f)类的先验概率P(Bl)为：

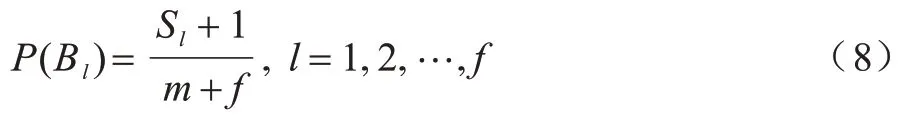
对5 种分类变量采用数值化描述，而这些信息数据近似为正态分布，因此采用高斯函数确定条件概率。条件概率如式（9）所示：

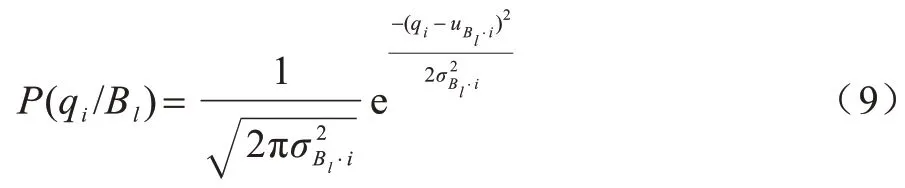
工作面煤与瓦斯突出预测的权重贝叶斯模型如式（10）所示：

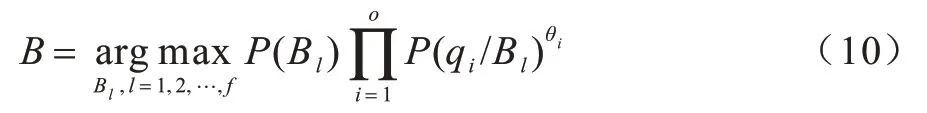
其中，B为贝叶斯最大后验概率值［23］，对应突出危险性等级。通过计算每个突出危险性等级的后验概率值，进而比较得到最大后验概率值以及对应的突出危险性等级。

2 基于预测模型的工作面煤与瓦斯突出预测

考虑工作面煤与瓦斯突出的多种影响因素，基于工作面煤与瓦斯突出预测的权重贝叶斯模型进行突出危险性等级预测。工作面煤与瓦斯突出预测的主要步骤如下：

步骤1通过多传感器在线检测或离线检测方式，获得反映工作面煤与瓦斯突出危险性的5 种分类变量动/静态数据。

步骤2对所得检测数据进行Z-Score 标准化处理，得到无量纲数据qi(i=1，2，…，o)。

步骤3将无量纲数据qi(i=1，2，…，o)作为工作面煤与瓦斯突出预测的权重贝叶斯模型的输入，计算得到工作面煤与瓦斯突出危险性等级的预测值B。

步骤4输出工作面煤与瓦斯突出预测的预测结果B，并将预测结果B存储到数据库。

工作面煤与瓦斯突出预测的过程如图2 所示。工作面煤与瓦斯突出预测的权重贝叶斯模型准确性与样本数据的完备性密切相关。工作面煤与瓦斯突出具有多样性、突发性、影响因素的不确定性、非线性等特点，而完备性的样本数据需要长时间积累过程，因此基于样本数据构建的突出预测模型需要适时更新才能保证模型预测的准确性。采用样本更新后进行模型重构的方法来完成工作面煤与瓦斯突出预测的权重贝叶斯模型更新。

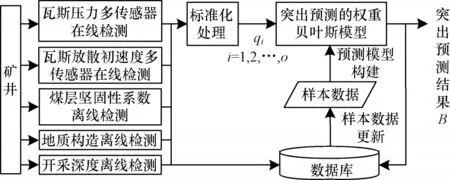
图2 基于PCA 和权重贝叶斯的工作面煤与瓦斯突出预测Fig.2 Prediction of coal and gas outburst in mine working face based on PCA and weighted Bayesian

如果新数据与样本数据有高相似度，则不进行样本数据更新；如果没有相似度，则将新数据存储到样本数据中完成样本数据的更新。

设新数据为Z={z1，z2，…，zo+1}，z1，z2，…，zo为5 种分类变量，zo+1为突出危险性等级数据，第k个样本的数据Xk={xk1，xk2，…，xko}，则z1，z2，…，zo与Xk的相似度为：

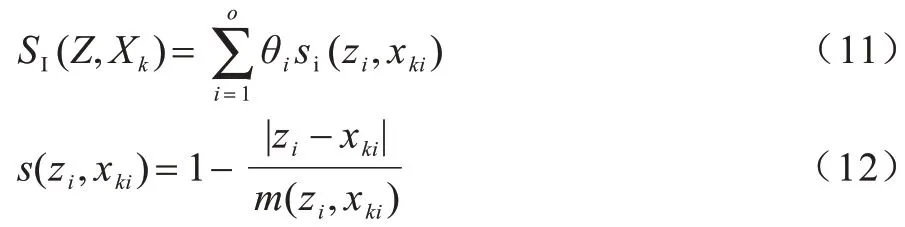
其中，θi为分类变量权值，si（zi，xki）为新数据中第i个元素与第k个样本的第i个元素的相似度。

当新数据Z满足式（13）时，将新数据Z存储到样本数据中。

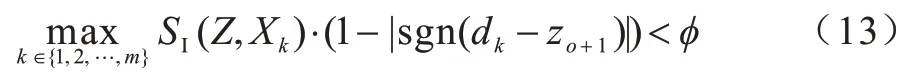
其中，φ为相似度阈值，sgn（）为符号函数，其表达式如式（14）所示：

3 实例验证

整理国内矿井工作面煤与瓦斯突出数据对本文方法进行验证。整理前15 组数据作为突出预测建模时的训练样本数据，训练数据的平行坐标如图3所示。后8 组数据作为测试数据。

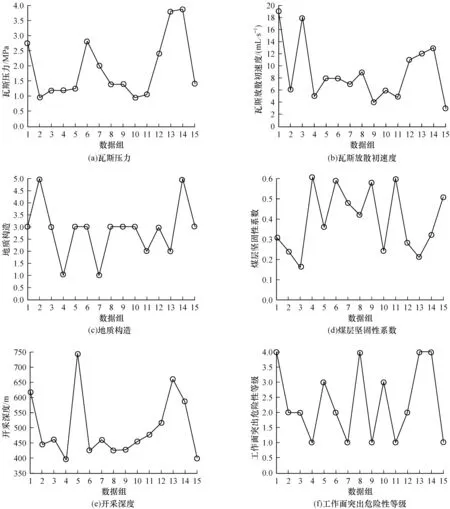
图3 训练数据的平行坐标图Fig.3 Parallel coordinates plot of training data

采用Python 语言对本文方法进行编程实现。令突出危险性等级数量f=4，训练样本数量m=15，分类变量数量o=5，主成分贡献率阈值δ=0.8，相似度阈值φ=0.90。利用图3 所示的训练数据，构建工作面煤与瓦斯突出预测的权重贝叶斯模型。其中，本文方法得到的分类变量权重为θ1=0.246 2，θ2=0.146 5，θ3=0.258 4，θ4=0.212 1，θ5=0.136 7 测试数据及其预测结果如表1所示。

本文方法对煤与瓦斯突出预测具有较高的准确率，采用图3 所示的训练数据，构建工作面煤与瓦斯突出预测的朴素贝叶斯（NBS）模型和专家给定分类变量权重的权重贝叶斯（EWBS）模型，并对测试数据进行突出危险性预测。利用NBS 模型进行突出预测的方法记为NBS 方法，而利用EWBS 模型进行突出预测的方法记为EWBS 方法。EWBS 方法与本文方法都是利用式（10）所示模型进行突出危险性预测。两种方法的区别在于分类变量权重确定方法不同，EWBS 方法的分类变量权重具有主观性，受专家经验知识影响，而本文方法的分类变量权重是通过对突出数据的主成分分析获得，具有客观性和科学性，对突出数据有一定的依赖性。NBS 方法可以看作是本文方法的特殊情况，即各分类变量权重值都为1 的预测方法。煤与瓦斯突出的发生受多种因素共同影响，但各因素对突出的影响不同。因此NBS方法是在较理想条件下实现，本文方法更符合实际。NBS 和EWBS 方法对测试数据的预测结果如表1 所示。EWBS 方法中的θ1=0.16，θ2=0.16，θ3=0.30，θ4=0.19，θ5=0.19。

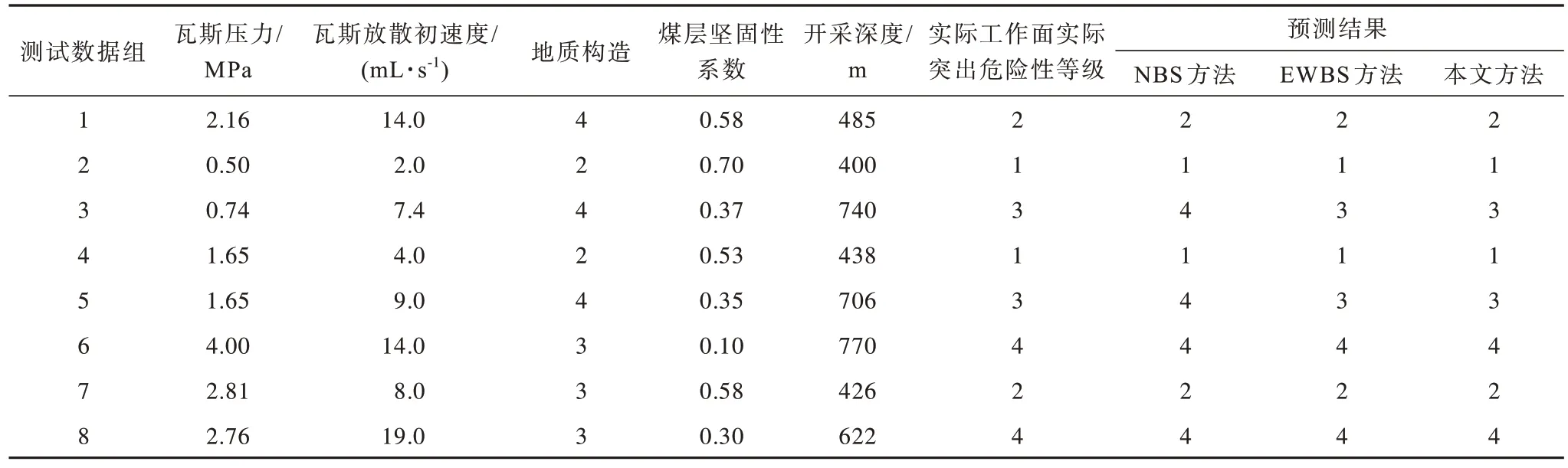
表1 测试数据及其预测结果Table 1 Testing data and prediction results

由表1 可知，本文与EWBS 方法所得的预测结果与实际完全一致，并优于NBS 方法，NBS 方法的预测结果准确率为75%。

本文方法和EWBS 方法针对测试数据进行突出预测时得到最大后验概率值如表2 所示。本文方法得到最大后验概率值均大于EWBS 方法，且预测不确定性优于EWBS 方法。相比专家给定方法，本文方法所确定的分类变量权重更合理。

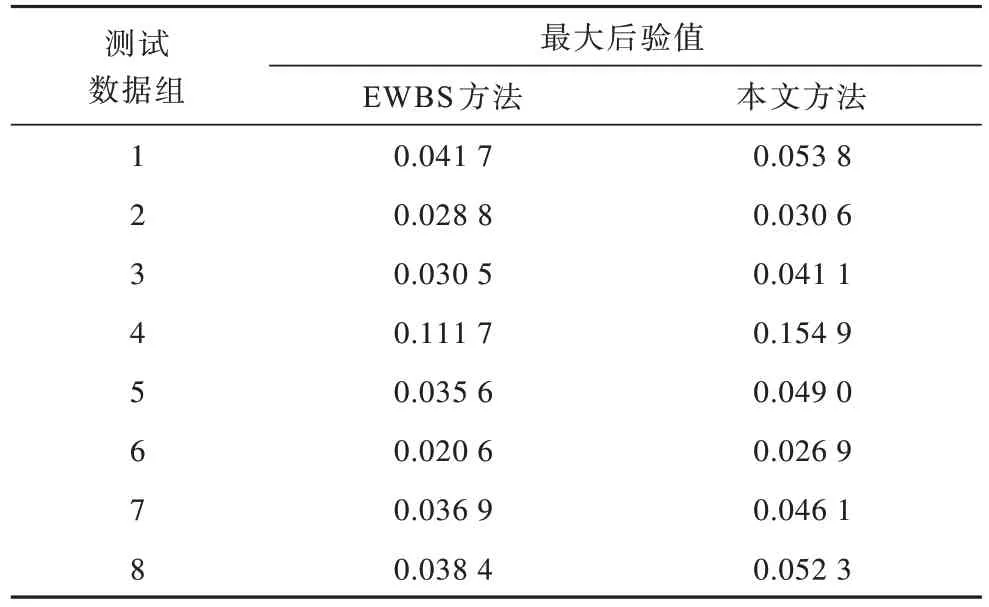
表2 最大后验概率值Table 2 Maximum posterior probability value

NBS 方法和本文方法建模所需的时间如表3 所示。本文方法建模所需时间仅为2.5 s，比NBS 方法建模时间多了1.1 s。而实际利用所建模型进行突出预测时间不超过10 ms，满足工作面煤与瓦斯突出动态预测的时间要求。

表3 建模时间Table 3 Time for building model s

4 结束语

本文将工作面煤与瓦斯突出预测问题归结为分类问题，考虑突出的动静多种影响因素，提出一种基于PCA和权重贝叶斯的工作面煤与瓦斯突出预测方法。实验结果表明，与朴素贝叶斯与权重贝叶斯模型相比，该预测方法具有预测准确性高、预测不确定性低、设置参数较少的特点，可以快速获得预测结果，为现场指导矿井工作面安全生产提供一定的参考。后续将在权重贝叶斯模型中融入电磁辐射、声发射实时因素信息，进一步提高突出预测准确性。