周期性风温下矿井巷道围岩换热教学实验装置研制*

刘 伟，梁书菲，黄庆威，刘晓薇，秦跃平，宋怀涛，郭开元

(中国矿业大学(北京)应急管理与安全工程学院，北京 100083)

0 引言

矿井热害是煤矿、金属矿山等深部开采过程中常见的灾害之一[1-2]。井下高温热环境会严重破坏人体热平衡，危害人员身体健康，降低工作效率，已成为制约采矿业向深部发展的关键因素[3]。深部矿井热源中，围岩散热量约占矿井总热源的55%左右[4]，而巷道风温随季节的周期性变化则大大增加了深部围岩传热的复杂性。因此，研究周期性风温作用下的巷道围岩换热过程对矿井热害治理具有重要意义[5]。

当前矿井热害相关课程的教学过程中，主要通过多媒体课件来对围岩传热理论[4-5]进行讲解，但风流—巷道围岩换热过程较为抽象，教学难度大。尽管数值仿真可以展示巷道围岩传热过程，但局限于虚拟技术，不能培养学生的实践动手能力[6-8]。因此，采用教学与相似模拟实验相结合的方法，有利于学生掌握周期性风温作用下矿井热害的发展演化规律，提高教学效率[9]。目前，采用物理实验模拟井巷围岩温度场分布的研究还较少[10]。Zhang等利用相似模拟实验分析了水文地质对围岩传热的影响[11]；王义江[12]研制了巷道围岩及风流非稳态传热传质实验系统；杨高飞[13]搭建了巷道传热传湿模拟实验台，可分析巷道围岩与风流间的传热传质；张源[10]等研制了高地温巷道热湿环境相似模拟实验系统，研究了高地温巷道围岩温度场及相关参数变化特征；Zhang等[14]基于相似模拟实验分析了地下水对空气与围岩换热的影响。上述研究中，多数将巷道风温视为恒定温度，这与实际巷道风温呈周期性变化的情况不相符，将会产生一定误差。

本文设计并搭建一种更接近实际矿井巷道围岩换热的实验测试装置，能模拟风流温度周期性变化下巷道非均质围岩的温度分布及其演变过程，依据实验数据能进一步定量估算围岩散热量，为井下热害评估提供理论依据。同时，实验过程可直观展示巷道围岩的传热规律，加深学生对传热理论的理解和掌握，提高学生动手实践能力。

1 实验原理

1.1 围岩传热数学模型

以深部圆形巷道为研究对象，假设：1)巷道壁面在暴露通风前处于原始岩温状态，无内热源；2)巷道轴向无温度差，换热条件一致；3)巷道风流温度保持稳定的周期变化状态，如式(1)所示[15]：

(1)

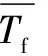
根据能量守恒定律和傅里叶定律，巷道围岩非稳态传热模型如式(2)所示：

(2)

式中：T为巷道围岩温度，℃；r为围岩到巷道中心的距离，m；r0为巷道半径，m；a为围岩导温系数，m2/s；λ为围岩体导热系数，W/(m·℃)；h为巷道壁面对流换热系数，W/(m2·℃)；Tgu为原始围岩温度，℃。

引用以下无因次准数将式(2)无因次化，得到：

则如式(3)所示：

(3)

式中：傅里叶数Fo、无因次年周期FoT、毕渥数Bi和无因次半径R均为无因次准则，无量纲过余温度Θ必为Fo、FoT、Bi和R的函数，如式(4)所示：

Θ=f(Fo,FoT,Bi,R)

(4)

1.2 巷道围岩温度场的相似准则

在相似模拟实验中，满足所有相似条件是难以实现的。因此，满足其中主要相似条件，从而达到满足工程所需要的近似相似。影响巷道围岩温度分布的无因次准数有无因次半径R、毕渥数Bi、傅里叶数Fo和周期傅里叶数FoT；影响巷道壁面对流换热的无因次准数有努塞尔数Nu、雷诺数Re和普朗特数Pr，如式(5)所示：

(5)

式中：d为巷道直径，m；u为风流速度，m/s；μ为空气运动黏度，m2/s；Cp为等压比热容，kJ/(kg·K)；λf为空气导热系数，W/(m·k)。

根据相似原理可知，要保证相似实验模型与原型相似，只要模型与原型的单值条件相似，且满足二者对应的无因次准数相等即可。具体相似条件如式(6)所示[16]：

(6)

式中：r、r′分别为模型与原型巷道围岩到巷道中心的距离，m；r0、r0′分别为模型与原型的巷道半径，m；h、h′分别为模型与原型表面对流换热系数，W/(m2·k);λ、λ′分别为模型与原型围岩导热系数，W/(m·k)；a、a′分别为模型与原型围岩导温系数，m2/s；τ、τ′分别为模型与原型巷道风流温度波动的年周期，s；ρ、ρ′分别为模型与原型的空气密度，kg/m3；u、u′分别为模型与原型的空气流速m/s；d、d′分别为模型与原型的巷道直径，m；μ、μ′分别为模型与原型的动力黏性系数，Pa·s；λf、λf′分别为模型与原型的空气导热系数，W/(m·k)；Cp、Cp′分别为模型与原型的等压比热容，kJ/(kg·K)。

巷道围岩温度场的原始物理模型和相似模型具有若干同名比例常数，包括几何相似比(Cl)、热扩散系数相似比(Ca)、时间相似比(Ct)、波动周期相似比(Cτ)、壁面对流换热系数相似比(Ch)、空气导热系数相似比(Cλ)和空气流速比(Cu)等，表达式如式(7)所示：

(7)

本实验中的通风介质为空气，无论气温是否变化，巷道相似模型与巷道原型中空气的ρ、μ、Cp、λf都一样，故相似模型的Pr数与原型的Pr数相等。只要保证模型与原型的Re相等，则其Nu必然相等。结合式(6)和式(7)，模型与原型的同名比例常数应满足式(8)：

(8)

2 实验方案

2.1 巷道围岩换热模拟实验平台

针对巷道围岩与风流之间的周期性换热特性，根据上述相似条件，自主设计研发矿井巷道围岩换热相似模拟实验平台，如图1所示。该平台由周期性风温控制及输出系统、非均质巷道模型主体和数据采集系统等组成。

图1 实验平台示意

周期性风温控制及输出系统主要由高低温交变实验箱、进风管道、回风管道组成，可调节的风流温度范围为-30 ℃～120 ℃，风流速度范围为0～6 m/s。非均质巷道模型主体尺寸为700 mm×700 mm×300 mm，外壳顶部和底部均设置50 mm厚的保温材料，模型主体内铺设5层热物理性质不同的相似材料，模拟巷道直径为100 mm。温度监测系统主要由热电阻温度传感器和数据采集器组成，可以实时采集温度信号，温度传感器布置截面如图2所示，各传感器间距为60 mm。

图2 测点分布示意

2.2 实验参数及过程

1)巷道围岩参数

相似实验模型只用于研究巷道围岩温度场的变化规律，故围岩相似材料在确保易于成型且具有一定的强度的前提下，只需考虑围岩的热物性参数即可。煤系地层中常见岩石的导热系数一般在0.25～2.6 W/(m·℃)之间[17]。若不针对特定岩性的巷道围岩，相似材料的导热系数选取在上述范围内即可。选取石膏、河沙、水泥、土和砂岩粉末等作为相似模拟材料。鉴于上述材料的导热系数总体低于煤系地层中岩石的导热系数，实验选用Fe2O3粉末作为促导材料提高相似材料的导热系数。利用正交实验设计方法，通过多组对比实验，对导热系数、密度和比热等参数进行测定，确定符合要求的各层材料配比，如表1所示。安装后的巷道围岩模型主体如图3所示。

表1 相似材料配比

图3 巷道围岩模型主体

2)巷道内风流参数

实验中，模拟巷道周期性风流平均温度为15 ℃，振幅为30 ℃，周期为5 h，原始围岩温度为23 ℃，风流速度控制在1.3 m/s左右。由Dittus-Boelter公式得到式(9)：

Nu=0.023Re0.8Pr0.4

(9)

将无因次准数带入式(9)，可得模拟巷道壁面对流换热系数的计算式，如式(10)所示：

(10)

空气导热系数设为0.025 W/(m·℃)，空气运动黏度为14.1×10-6m2/s，根据式(10)可求得对流换热系数为28.38 W/(m·℃)[18]。

3)实验过程

实验前，按比例配备相似材料，并在恒温恒湿箱中养护至设定的原始岩温(23 ℃)。随后，采用直接浇筑的方式布置模拟巷道及其围岩，安装进、回风管路，按照设计要求布点温度探头，通过信号传输线与数据采集器进行连接。巷道模型的四周用保温材料包裹以减少热损失，最后将进、回风管路与高低温交变实验箱的进出风口连接在一起。实验中，首先打开数据采集系统，检查电力系统是否畅通，对测点温度进行测试及校正，再开启高低温交变实验箱，输入设定的供风参数(平均风温15 ℃，振幅30 ℃，周期5 h)，记录各测点温度变化。

3 实验结果和讨论

3.1 围岩体内部温度波变化规律

为研究非均质对围岩温度场的影响，选取模拟巷道顶板与底板各层测点温度数据进行分析，如图4所示。可以看出，通风开始后，在周期性风流温度影响下，围岩体内部迅速产生周期性温度波，但温度波的振幅随着围岩体深度增加而逐渐减小，越靠近巷道壁，温度波的振幅越大。当距壁面120 mm深时，围岩温度波的振幅已接近于0。随时间增长，各测点平均温度呈不同幅度的下降，壁面处测点5和11的平均温度经计算从初始的23 ℃降低到17.5 ℃；距壁面远处的测点2和测点14处温度降幅最小，约为2 ℃。沿巷道径向，不同深处围岩温度波的极值会发生滞后现象，且深度越深，温度波滞后越明显。

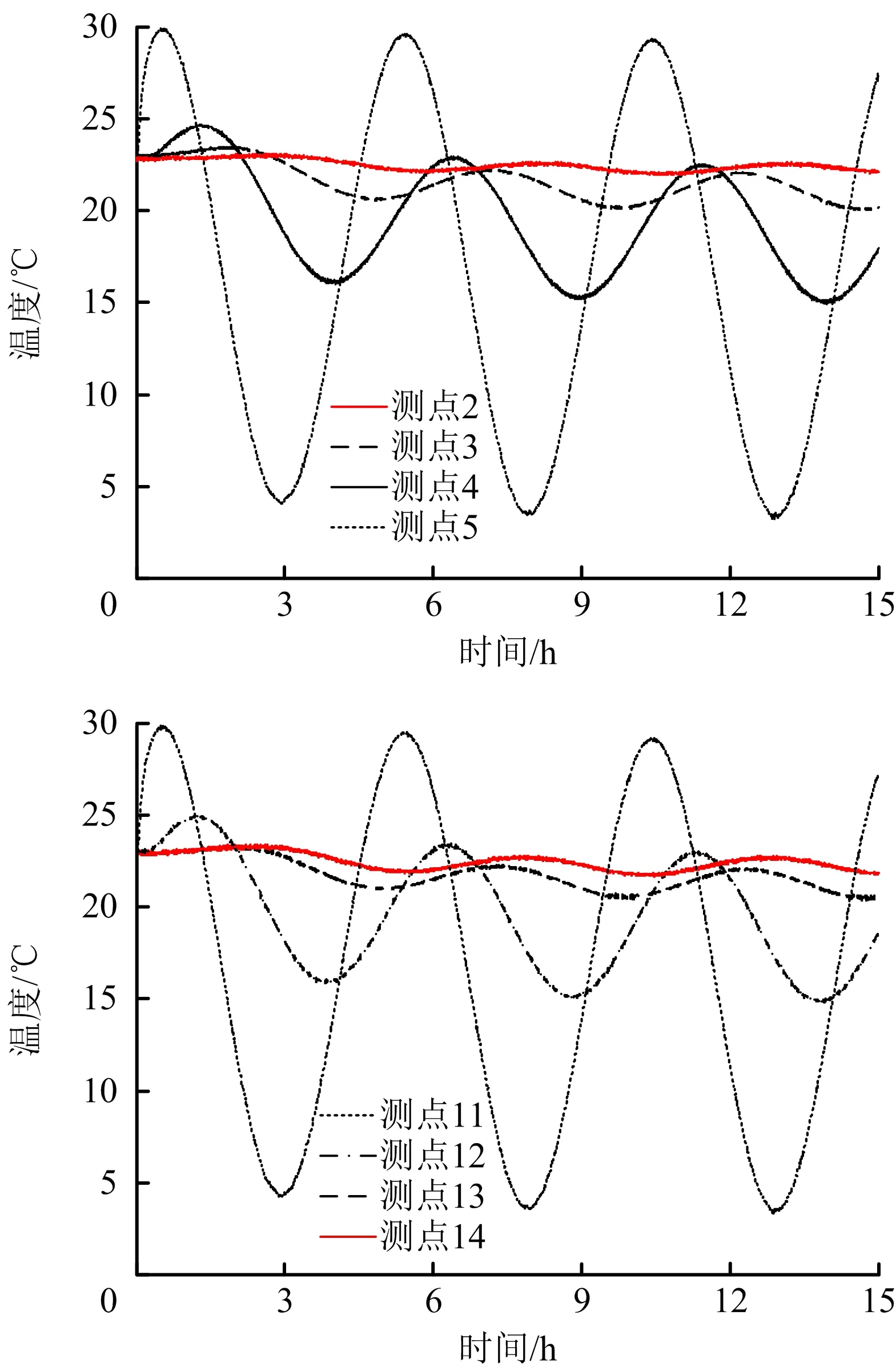
图4 围岩不同测点温度随通风时间的变化曲线

3.2 周期性风流温度对非均质围岩温度场的影响

煤系地层中，矿井巷道围岩往往为层状各向异性，周期性风流进入巷道后温度波在不同层位上扰动，该扰动对非均质围岩体的调热能力具有显著的影响，选取模拟巷道围岩体不同层位上的测点进行研究，如图5所示。

图5 等距测点温度波动曲线

图5所示，在壁面处，围岩体温度波动相对稳定，而距壁面60 mm、120 mm及180 mm处，温度波的峰值在不同周期下有着明显的下降趋势。此外，由于测点3、测点8和测点13处导热系数依次递增，由图5(c)中可以看出，测点13处的围岩温度波动振幅最大，而测点3处的最小，可见周期性风流温度对测点13处围岩的调热影响最大。图5(d)同样可以得出类似结论，即在非均质巷道围岩体中，围岩体所在岩层导热系数越大，周期性风温调热的影响越大。

3.3 围岩热流密度及散热量

由于巷道围岩与风流之间存在温差，故巷道壁面处存在对流换热。根据牛顿冷却公式，壁面处的热流密度如式(11)所示：

q=-h′(T|r=r0-Tf)

(11)

式中：T|r=r0为巷道壁面温度，℃，可取测点5、测点6和测点11这3点的平均温度。

图6为巷道风温、围岩壁面温度及壁面热流密度的波动曲线。曲线的拟合公式见表2。可以看出，与风温相比，巷道壁面温度均值更大、振幅更小且有一定的滞后性，受深部围岩高温影响，壁面平均温度比巷道风流平均温度高1.48 ℃。随着风温和壁温差的增加，热流密度随之增大，故热流密度也随时间呈周期性变化。当两者温差为0 ℃时，如t1、t2、t3时刻，热流密度值为0。此外，周期性热流密度均值为负值，表示围岩整体处于放热状态。

图6 巷道风温、壁面温度及热流密度波动曲线

表2 巷道风温、壁面温度及热流密度波动曲线拟合公式

对热流密度按时间周期进行积分，得到围岩散热量计算式，如式(12)所示：

(12)

式中：Q为周期围岩散热量，kJ/m2；tn为第n个年周期时间，s；tn+1为第n+1个年周期时间，s。

实验中，5 h对应1个年周期。图7为围岩壁面单位面积的年周期散热量变化曲线。可以看出，围岩年散热量在初期随时间快速下降，而后逐渐趋于平稳，最终在1.3×104kJ/m2上下浮动。需要说明的是，该数据只对本次模拟巷道有效，它受围岩导热系数、孔隙率的影响。

图7 围岩年周期散热量随时间变化曲线

4 结论

1)搭建巷道非均质围岩换热实验平台，能够测试周期性风温影响下围岩体各处温度的变化情况，依据温度测试数据能够计算出围岩壁面热流密度及围岩体散热量。结果表明，周期性风温影响下，巷道围岩体内部温度也呈周期性波动；对于非均质围岩体，岩层导热系数越大，周期性风温对围岩的调热影响越大；巷道壁面处热流密度也随时间呈周期性变化，围岩壁面年周期散热量则随时间呈下降趋势，最终稳定在1.3×104kJ/m2左右。

2)采用理论结合实验的方式，直观地将巷道围岩换热变化过程展现给学生，既能加深学生对巷道围岩温度场分布规律及影响因素的认识和理解，也能锻炼和提高学生的科研能力。

3)该实验平台还支持开展与矿井热害评估相关的开放性实验。根据相似理论按照一定比例缩小原型的几何尺寸、时间等条件，由相似模拟实验得到围岩内部温度场的变化规律，再将该变化规律依据相似比准则反推到原型巷道围岩，用以评估现场巷道围岩换热情况。