基于地理加权回归张力样条函数的广西PM2.5浓度插值

谢劭峰，魏朋志，黄良珂*，张 伟，黎峻宇

(1.桂林理工大学测绘地理信息学院，桂林 541006；2.广西空间信息与测绘重点实验室，桂林 541006)

大气霾污染因其对人体健康、生态环境和气候变化的影响而成为全球关注的严重环境问题，PM2.5是霾污染的主要原因[1]。中外学者对PM2.5预测研究热度也在不断提高。周体鹏[2]基于克里金插值法对昆明市PM2.5浓度变化进行了估算；卢月明等[3]基于局部加权线性回归模型提出了一种引入正则化项的空间插值方法，该方法提高了PM2.5插值效果；谢劭峰等[4]对南宁市PM2.5浓度与气象因素的关系进行了探讨并结合多种气象因素运用多元线性回归模型对其浓度变化进行了预测；王德冬等[5]利用时空回归克里金法对区域PM2.5进行了时空建模及插值；王娟[6]利用灰色关联度、多元回归分析等方法定性定量分析了中国30个代表城市的污染程度及污染规律；胡稳等[7]利用普通克里金(ordinary Kriging，OK)法进行空间插值获取PM2.5、PM10分布特征并比较了6种半变异函数模型的适用性；Masood等[8]建立了基于机器学习方法的PM2.5预测模型；焦利民等[9]基于土地利用回归模型进行了武汉市PM2.5浓度高分辨率空间分布模拟研究；李爽等[10]将主成分分析与逐步多元线性回归相结合,提出了一种改进的土地利用回归模型模拟大区域PM2.5浓度空间分布的方法;刘妍月等[11]运用多种插值方法对长沙市大气中PM2.5浓度分布进行比较研究，发现基于反距离加权的克里金插值方法效果较好；车磊等[12]运用一种基于多尺度最小二乘支持向量机优化的克里金插值方法对青岛市PM2.5浓度变化进行插值计算，效果优于传统克里金模型插值效果；赵阳阳等[13]运用协同时空地理加权回归PM2.5浓度估算法对京津冀地区进行实验，实验效果较传统单一核函数时空地理加权回归模型有所提升；陈辉等[14]利用地理加权回归模型进行全国区域PM2.5遥感估算，其效果优于多元线性回归模型；邓悦等[15]以北京市为实验区域，在地理加权回归模型基础上加入了贝叶斯先验信息以降低弱数据对回归模型的影响。

上述方法在一定条件下都取得了较好的预测效果，但这些方法并没有对模型的回归残差进行很好的处理。另外PM2.5存在着很强的空间异质性和空间非平稳性，上述模型难以处理或同时处理这两个PM2.5分布特征。现以广西地区49个空气质量监测站点和18个气象监测站点2018年监测数据年均值为数据基础，建立地理加权回归张力样条函数(geographically weighted regression-tension spline function, GWR-TSF)组合模型进行PM2.5浓度插值，并与克里金和地理加权回归模型进行对比。

1 数学模型

1.1 克里金插值

克里金(Kriging)是一种依据协方差函数对随机过程或者随机场进行空间建模和插值的回归算法，在特定的随机过程，例如固有平稳过程中，克里金法能够给出最优线性无偏估计，因此在地统计学中也被称为空间最优无偏估计器，该方法不仅考虑被估点位置与已知数据位置的相互关系，而且还考虑已知点位置之间的相互联系，因此更能反映客观地质规律，估值精度相对较高，该方法的适用条件为区域化变量存在空间相关性，其原理[16]可表示为

(1)

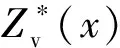
1.2 地理加权回归

地理加权回归(GWR)是一种空间分析技术。空间数据一般具有空间非平稳性的特征，用一般线性回归模型来拟合空间数据，其分析结果不能全面反映空间数据的真实特征。GWR是一种相对简单而又有效的探测空间非平稳性的方法，属于局域空间分析模型。它允许不同的地理空间存在不同的空间关系，其结果是局域而不是全域的参数估计，因此能够探测到空间数据的空间非平稳性。GWR通过建立空间范围内每个点处的局部回归方程，来探索研究对象在某一尺度下的空间变化及相关驱动因素。由于它考虑到了空间对象的局部效应，因此其优势是具有较好的准确性，其基本原理[16]可表示为

(2)

式(2)中：(ui,vi)为第i个采样点坐标；βk(ui,vi)为第i个采样点上的第k个回归参数；xik为第i个观测点的第k个影响变量；p为影响变量个数；εi为回归残差。

1.3 地理加权回归张力样条函数插值

地理加权回归张力样条函数(GWR-TSF)插值是一种将地理加权回归(GWR)与张力样条函数(TSF)插值结合起来的综合分析方法。GWR模型是对普通线性回归模型的扩展；张力样条函数是径向基函数插值法的一种，该方法插值速度快以及估测大小的范围不局限，张力样条函数的基本原理[17]可表示为

(3)

式(3)中：S(x,y)为插值结果；a为趋势函数；N为插值区域点的个数；λj为通过求解线性方程组获得的系数；rj为点(x,y)到第j个点的距离；φ为权重参数；k0()为修正贝塞尔函数；c为常数，c≈0.577 215。

GWR-TSF模型利用张力样条函数对GWR模型得到的回归残差ε进行空间插值，然后将得到的残差插值结果与GWR回归估计值进行叠加，从而获得GWR-TSF模型估算值，其原理可表示为

GWR-TSFPM2.5=GWRPM2.5+TSFGWRr

(4)

式(4)中：GWR-TSFPM2.5为GWR-TSF模型对PM2.5的浓度估算值；GWRPM2.5为GWR模型对PM2.5的浓度估算值；TSFGWRr为TSF插值法对GWR模型估算PM2.5的浓度值后产生的回归残差进行区域插值得到的结果。

2 实验数据

以广西地区2018年的气象和空气质量参数年均值为实验数据，广西地区气象监测站点为18个，采集其站点2018年年均气温、风速、气压和降水量等气象数据，数据来源为中国气象科学数据共享服务网，空气质量监测站点为49个，选择其中7个站点作为模型验证集，42个站点为模型训练集，采集其站点2018年年均PM2.5、CO、SO2、NO2和O3等大气因子浓度数据，数据来源为环境专业知识服务系统http://envi.ckcest.cn/environment/，站点分布如图1所示。

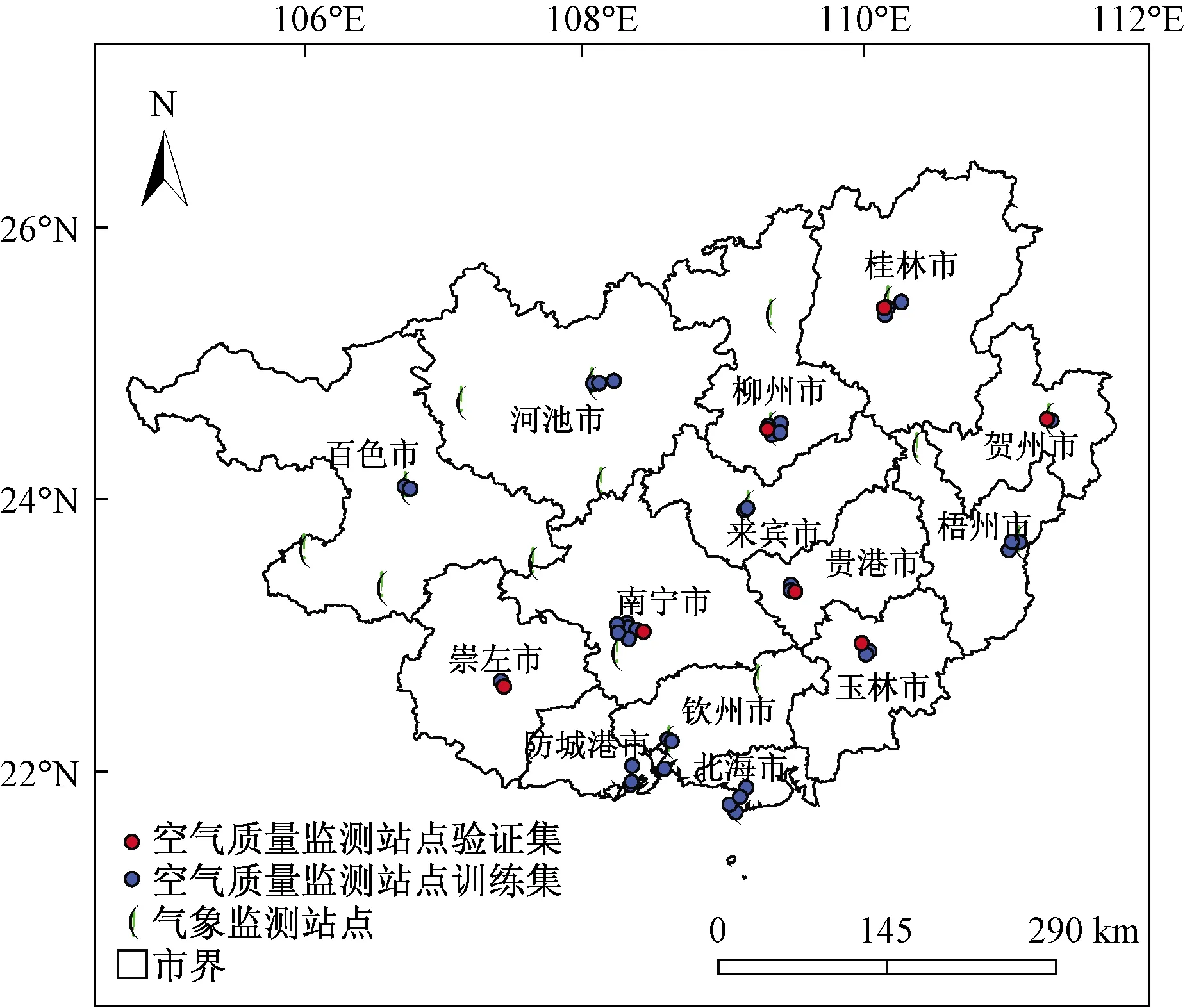
图1 广西气象站与空气质量监测站分布

3 实验结果分析与讨论

3.1 克里金模型

以广西地区空气质量监测训练集42个站点2018年PM2.5浓度年均值数据为基础，依据式(1)建立广西地区克里金模型，得到的克里金插值结果如图2所示。

图2 克里金法PM2.5插值结果

从图2可以看出，广西地区的PM2.5浓度分布情况主要为东高西低，最严重的区域主要集中在柳州市和来宾市一带。

3.2 地理加权回归模型

因为GWR模型为回归模型，具有参考多个解释变量建模的优势，由于空气质量监测站点只能得到各类大气污染物含量数据，并不能有效获取其站点位置的气象数据，而广西地区的气象监测站数量较少，因此为了有效得到各个空气质量监测站点的气象数据，采用反距离加权插值法对气象站点气温、风速、气压以及降水量进行空间插值，并将其对应的插值结果提取至各个空气质量监测站点，各气象参数插值结果如图3所示。

图3 气象参数反距离加权插值结果

在得到各气象参数插值结果后，将其值提取到各个空气质量监测站点，得到各站点的气象参数数据。由于GWR模型不能对具有多重共线性的变量进行建模，所以找到合适的变量组合是完成模型的前提条件和关键因素，因此在建模之前还应当对空气质量监测站点的各类数据进行共线性诊断，得到的结果如表1所示。

从表1中方差比例来看，除第7维度中有两个变量(CO和NO2)方差比例同时高于50%以外，其余维度中均最多只有一个变量方差比例高于50%，因此不具备多变量存在多重共线性的判断条件；而从条件指数来看，条件指数为最大的主成分与当前主成分比值的平方根，从第6维度到第9维度的条件指数均大于30，即存在多个维度条件指数大于30，证明此处用于建模所选的8类变量之间存在着多重共线性，而多重共线性是指回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确，因此需要剔除掉一些多余的变量才能进行建模实验，经过反复比较实验，最后得到的变量组合为CO、SO2、NO2和风速，变量组合共线性诊断结果如表2所示。

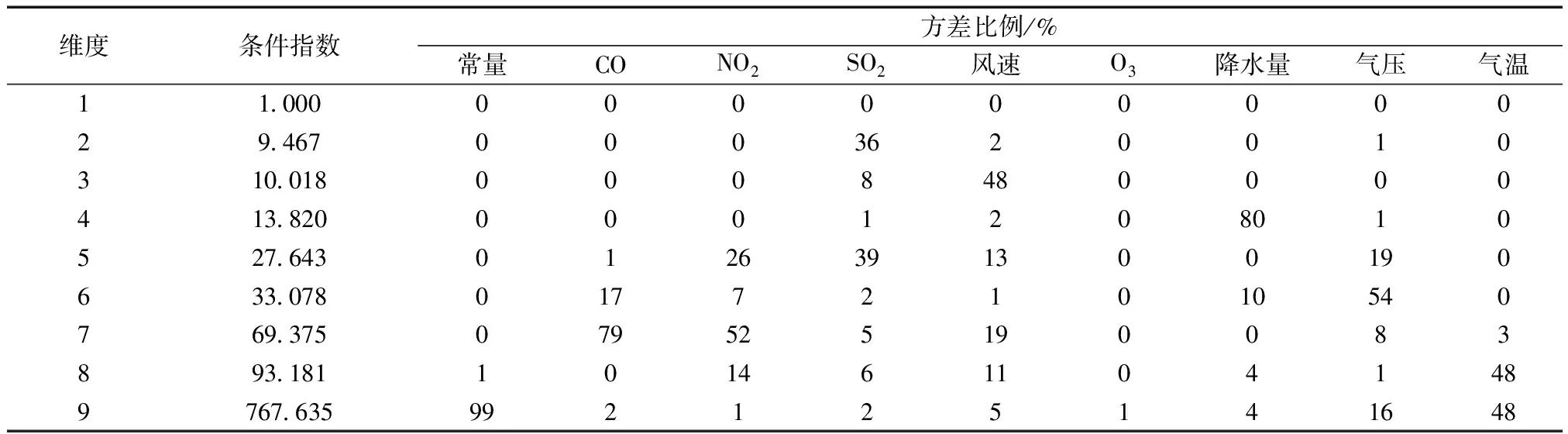
表1 变量共线性诊断结果

从表2中数据可以看出，所有维度条件指数均小于30，方差比例也没有出现某一维度具有多个高于50%的变量，说明各变量间不存在强多重共线性，可以用于模型构建。确定变量组合后，以广西地区42个空气质量监测站点作为训练集，7个空气质量监测站点作为验证集建立GWR模型，模型解释变量为CO、SO2、NO2和风速，得到的GWR验证集结果如图4所示，其模型残差结果如图5所示。

表2 CO、SO2、NO2、风速共线性诊断结果

图4 GWR验证集结果

图5 GWR残差

从图4可以看出，基于GWR模型得到的验证集站点PM2.5浓度的大小与分布规律同克里金插值法所得到的插值结果大致相同，以柳州市和贵港市一带区域数值最高。由图5的残差结果分析可知，残差绝对值较大的区域也主要分布于广西中东部地区。

3.3 地理加权回归张力样条模型

在完成GWR模型对该地区PM2.5浓度估算以后，对GWR残差进行空间自相关分析，其结果如表3所示。

表3中，MoranI指数为正，说明残差呈空间正相关，其值越大则空间相关性越明显，Z得分和P值分别表示标准差的倍数和空间分析中产生随机事件的概率，GWR残差Z得分为3.429，P值为0.001，则表示随机产生此聚类模式的可能性小于1%，结果可信，可根据GWR残差的空间自相关性运用张力样条函数对其进行空间插值运算，结果如图6所示。

表3 GWR残差空间自相关分析

从图6中对于GWR残差的张力样条函数插值结果可知，广西地区GWR残差值的分布规律为中东部区域数值为正，其绝对值较大的区域主要位于柳州、来宾、贵港、梧州、贺州和桂林六市；而广西南部区域残差多呈负值，其绝对值较大区域以南宁、崇左、防城港、钦州、北海和玉林六市为主。

完成残差插值计算后得到的张力样条函数插值结果提取值至验证集站点得到新的残差结果，接着将GWR预测值与插值处理后的残差值进行叠加运算便得到了GWR-TSF模型的最终插值结果，对7个验证集站点由3种模型得到的插值结果与真实值对比，结果如表4所示。

表4 验证集数据对比

3.4 插值结果评估

为了更直观地评价各模型的性能，采用均方根误差(root mean square error, RMSE)以及平均绝对误差(mean absolute error, MAE)对插值结果进行精度评定，相应的计算公式为

(5)

(6)

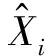
3种模型插值精度统计结果如表5所示。

表5 插值精度对比

从表5可以看出，GWR-TSF组合模型插值精度最高，GWR-TSF组合模型均方根误差的值较前两种模型分别提高了20.68%和25.71%，而平均绝对误差的值也分别提高了20.22%和11.62%，提升幅度基本都在20%左右，说明该组合模型在区域性插值PM2.5这一类空间异质性较强的变化因素时，效果要优于传统的单一模型。

4 结论

主要以广西地区空气质量监测站点和气象站点监测数据为基础，运用了3种模型对广西地区进行了PM2.5浓度插值分析，证明了GWR-TSF组合模型效果相较于传统的克里金模型和地理加权回归模型精度更好，更适用于广西地区PM2.5浓度插值研究，不过由于获取的气象监测站点较少，气象数据插值后的结果多重共线性现象严重，因此对模型的精度产生了一定的影响，该组合模型仍然有很大的改进空间。