切削加工表面粗糙度理论建模综述

2021-08-20马廉洁陈景强周云光

科学技术与工程 2021年21期

马廉洁，陈景强，王馨，周云光

(1.东北大学机械工程与自动化学院，沈阳 110819；2.东北大学秦皇岛分校控制工程学院，秦皇岛 066004)

切削加工在制造业中得到了广泛的应用，如机床、车辆、飞机[1-2]、光学元件和模具[3]等关键机械零件的加工。表面粗糙度是表征表面质量的重要参数，能够影响机械零件的力学性能、疲劳强度、配合性质、耐腐蚀性和润滑性等[4]。例如，当金刚石车削表面粗糙度超过阈值[5-6]时，光散射现象严重依赖于其光学性能。因此，表面粗糙度作为切削表面质量的一个重要指标[7-8]，在过去的几十年中受到了广泛的关注，然而，由于对切削加工影响因素的机理认识不完全[9-10]，在切削加工过程中获得满意的表面光洁度仍然很大程度上依赖于人工经验。因此，选择不当工艺参数和机床必然导致高产成本和低表面质量[11-12]。因此，探索和研究表面粗糙度的形成及切削加工表面粗糙度的精确模型。提高零件性能和使用寿命，需要将表面粗糙度控制在合理范围内[13]。目前，针对磨削和车削的研究较为广泛[14]。一般来说，切削表面粗糙度的建模方法可分为理论建模方法和经验建模方法。理论建模方法一般是根据切削过程中观察到的物理现象来实现的，如车削表面沟壑的周期性重复，或塑性侧流和材料回弹引起的材料膨胀。也就是说，粗糙度理论模型是在充分考虑这些观察到的现象的情况下进一步分析的。相比之下，经验模型则是直接根据切削深度、主轴转速、进给速度等工艺参数和相应的表面粗糙度值进行经验参数化建模。经验方法包括响应面方法、人工神经网络方法、回归分析法等。综上所述，理论建模方法侧重于表面形成的潜在机理，而经验建模方法侧重于实验过程中产生的数据分析。因此，现对中外切削粗糙度理论建模的方法进行综述，以车削为主。同时，建立“简单”和“复杂”建模因素的定义，对各种影响因素进行了分类，阐述影响表面粗糙度的各个因素，并对不同方法的特点和使用情况进行总结，最后对每种因素粗糙度建模方法的优势和不足进行分析。

1 表面粗糙度的分类及其简介

1.1 二维粗糙度评定参数

中国现行国家标准《产品几何技术规范(GPS)表面结构轮廓法术语、定义及表面结构参数》(GB/T 3505—2009)规定了5类共计15个参数或者曲线来评价表面粗糙度[15]，包括高度特征参数、间距特征参数和形状特征参数，其中高度特征参数中的轮廓算术平均偏差Ra、轮廓最大高度Rz和评定轮廓的均方根偏差Rq是3个最常用的参数。轮廓算术平均偏差Ra是指在取样长度(lr)内轮廓偏距绝对值的算术平均值。取样方式如图1所示，在实际测量中，测量点的数目越多，Ra越准确，其计算公式为

图1 轮廓算术平均偏差Ra取样图

(1)

式(1)中：l为单位内取样长度；Z(x)为取样长度内的纵坐标。

评定轮廓的均方根偏差Rq是在一个取样长度内纵坐标Z(x)的均方根值，定义为

(2)

图2展示了具有可见车削痕迹的脆性车削表面的三维表面粗糙度参数的经典计算过程。

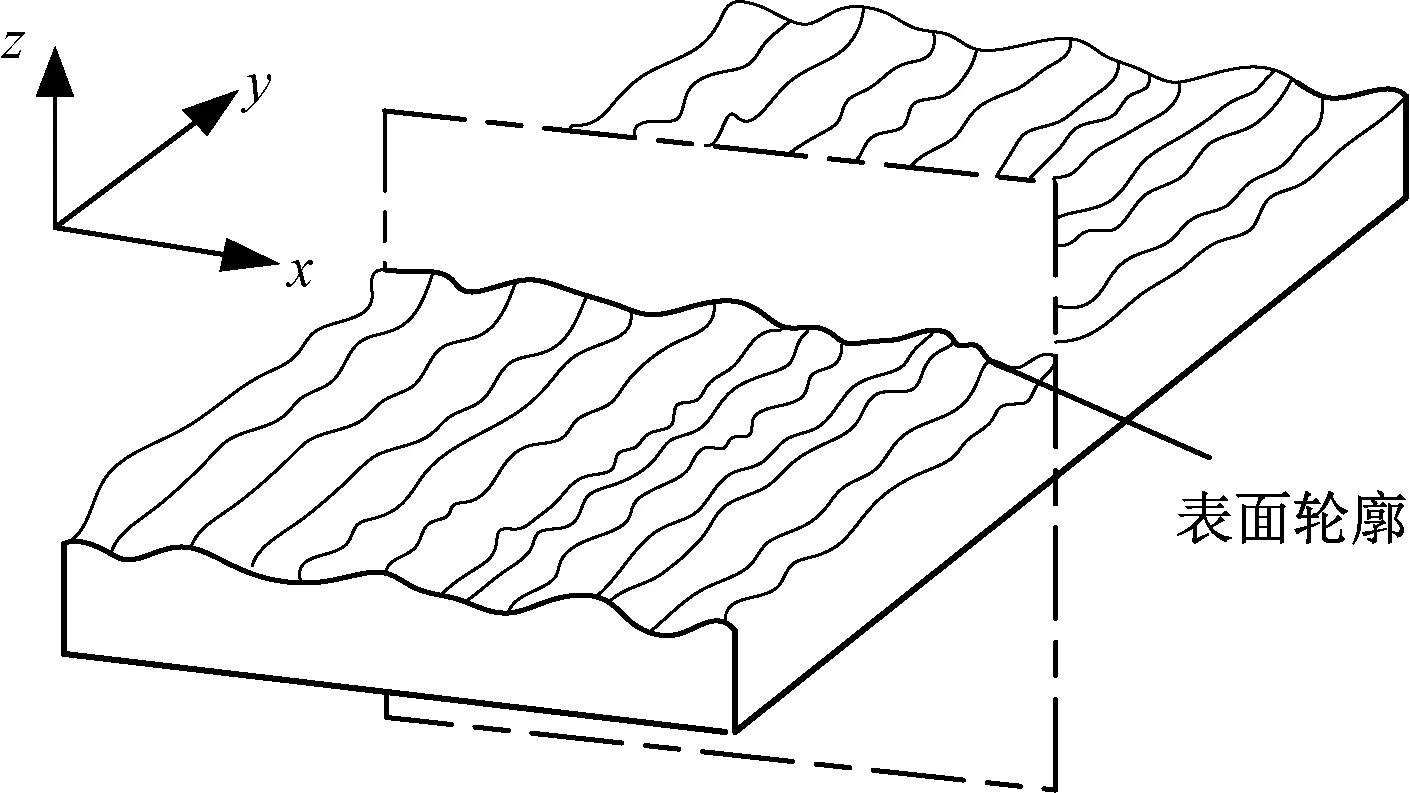
图2 表面轮廓图

1.2 三维表面粗糙度评定参数

目前ISO定义了一些三维表面粗糙度的评定参数[16]，常用参数有3种，包括：表面最大高度Sz，三维轮廓的均方根偏差Sq以及三维轮廓的算术平均偏差Sa。这些参数是在一个表面上而不是在一条直线上计算出来的，类似于二维表面粗糙度参数的定义方法，首先，还应使用相应的滤波器来获得粗糙度剖面，然后用最小二乘法确定一个平均平面函数，即参考平面，该方法类似于在获取二维粗糙度轮廓中平均线的作用。最后，利用参考平面计算了三维粗糙度参数。三维表面粗糙度的定义为

Z(x,y)=f(x,y)-ξ(x,y)

(3)

式(3)中：f(x,y)为原始定义的平面；ξ(x,y)为基准平面。

三维轮廓算术平均偏差Sa定义为

(4)

式(4)中：S为三维轮廓的单位面积。

三维轮廓均方根偏差Sq定义为

(5)

2 表面粗糙度的理论建模方法

车削过程中，由于刀具的轴向进给，已加工表面会留下周期性的沟槽。最基础的粗糙度模型只考虑刀具与工件材料的干涉关系，因此该模型被称为运动学模型，表达式为

Rt=f2/8rε

(6)

式(6)中：Rt为单位长度内最高点与最低点的距离；f为进给量；rε为刀具圆弧半径。然而，实际车削表面粗糙度受多种因素影响，如加工工艺参数、刀具几何形状、工件材料的塑性侧流、工件材料的弹性回复和机床振动等，这些因素会在理想残留轮廓的基础上增大表面粗糙度。由图3可以看出，车削表面粗糙度与机床、刀具、工件材料、环境等有关，影响因素包括机床的运动学和动力学特性、刀具的几何参数、工件材料和冷却液的特性等。

带星号(*)的参数是目前中外研究较少和难以实现的因素

2.1 机床因素对表面粗糙度的影响

机床对表面粗糙度的影响分为运动学方面和动力学方面。运动学因素是车削速度、车削深度和进给量。总体来说，进给量对于表面粗糙度的影响将会大于切削速度和切削深度。这主要是因为进给量会体现在已加工表面形貌中，是对刀具的一种复写，决定了在车削中刀具刀刃部分的大小。现将进给量同刀具因素一同考虑。刘献礼[17]研究表明，在硬态切削过程中，控制高速度、小进给量、小切削深度是获得较低粗糙度的最佳切削方法。其中切削深度对表面粗糙度的影响较大。马廉洁等[18]将车削过程分为挤压与切削两个阶段，分析了车削深度、车削速度和进给速度对表面粗糙度的影响规律，随着进给速度的增加，在挤压阶段刀尖和工件的接触区域产生更深层裂纹，切削阶段材料崩碎加剧，随着切削深度的增加，刀具与工件挤压作用增强，表面损伤加重。Grzesik[19]考虑精密车削过程中的运动学参数和最小未变形切削厚度，提出了一个粗糙度修正模型。Arunachalam等[20]讨论了切削速度对CBN刀具表面粗糙度的影响，随着切削速度的增加，温度迅速升高。随着切削温度的升高，变形材料的软化程度越来越高，高温对表面光洁度影响较大，会使磨损加剧。Wang等[21]通过正交实验回归分析，建立了基于刀头半径、进给速度、切削深度、切削速度和离散角5个主要切削参数的透镜表面粗糙度预测的指数模型。同时，建立了基于径向基函数最小二乘支持向量机的表面粗糙度预测模型。Sahin等[22]采用立方氮化硼刀具在不同条件下对AISI 1050淬火钢进行了车削试验，应用响应曲面法建立了表面粗糙度模型。除了运动特性外，机床的动态特性，特别是刀具与工件之间的振动，对表面粗糙度的形成也起着至关重要的作用。刀具与工件之间的振动模型可以简化成如图4所示的刀具振动模型。

kr为劲度系数；m为物体质量；cr为阻尼系数；Fr为进给抗力；Fc为主切削力；n为转速；h(0)为工件初始基准平面；h(t)为振动之后高度；x(t-τ)为某时刻位移变化量

在考虑了机床的动态特性影响下，Kim等[23]认为在金刚石车削加工表面时，不可避免地会在刀具和工件之间产生一定程度的相对振动，从而影响表面质量。他们将刀具和工件之间的振动简化为简谐振动，进行了金刚石车削光学表面刀具振动效应的微观形貌分析，进而建立了超精密切削振动影响下的三维形貌模型。Skelton[24]考虑了相邻两个进给速度之间的振动影响，提出了一个基于运动特性的表面粗糙度模型，该模型可以用于加工表面粗糙度的计算。Hocheng等[25]考虑了振动幅度，分析了粗糙度廓线的频率和大小，建立了与刀具几何形状、低频振动和测量仪器精度有关的Rq表面粗糙度模型。基于主轴动力学模型，研究了刀尖振动对表面生成[26]和表面粗糙度的影响[27-28]。针对具有代表性的刀尖振动条件下加工表面粗糙度的测量[29]，总结了金刚石车削加工中纳米表面生成的特征[30]。在车削加工过程中，振动是一个很复杂的问题，在切削加工过程中存在着一些不可控的因素，很难有统一的振动模型考虑到粗糙度理论模型中。因此很多学者采用间接法来求解问题。Kurniawan等[31]研究了椭圆振动辅助切削的粗糙度理论模型。裴宏杰等[32]采用正态分布、指数分布、Gamma分布、Weibull分布和Cauchy分布等函数拟合，根据赤池信息量准则(Akaike information criterion，AIC)确定出最优分布函数，采用极大似然法估计出未知参数。使用Gaussian Copula等拟合出振动和表面粗糙度之间的关系，并分析了振动与表面粗糙度之间的整体相关性。金成哲等[33]分析了车削细长轴的振动特性，建立了不同装卡方式下刀具-刀柄-主轴的有限元模型。Zhang等[34]建立了空气静压轴承主轴的五自由度动力学模型，描述了轴承的平动运动和倾斜运动的动力学响应，分析了超精密金刚石车削(ultra-precision diamond turning，UPDT)中不同切削过程对主轴表面形貌的影响。并得出在超精密金刚石车削加工中，静压轴承主轴振动是影响表面形貌的主要因素。进一步推导了空气静压轴承主轴五自由度动力学模型的数学解，探讨了主轴振动的自然机制，通过切削力的频率特性，模拟表面形貌的周期性。

2.2 刀具因素对表面粗糙度的影响

刀具对表面粗糙度的影响主要包括以下两类。第一类是刀具的几何参数对表面粗糙度的影响，主要包括刀具角度、刀尖圆弧半径和刀具的切削刃钝圆半径等与刀具生产制造相关的因素。第二类是刀具材料的种类。在车削加工过程中，刀具对表面粗糙度的影响很大程度上取决于工件材料的性能。表1详细总结了运动学和动力学下的刀具主偏角kr、刀具副偏角k′r和刀尖半径rε对表面粗糙度的影响。

表1 运动学和动力学模型

Vajpayee[35]进一步考虑了进给速度和刀具刃口形状的影响，分别提出了圆形刀具和直形刀具的Rt表面粗糙度模型。Sung等[36-37]在运动学模型的基础上，又考虑了刀具楔角对表面粗糙度的影响，建立了包含进给量f、刀尖圆弧半径rε和刀具楔角βo的算术平均粗糙度(Ra)模型和均方根粗糙度(Rq)模型，AISI 304 alloy steel精密车削实验结果表明模型精度优于几何模型。在脆性车削加工中，马廉洁等[38]基于脆性断裂力学和刀具-工件干涉原理，建立氟金云母陶瓷车削表面粗糙度理论模型，用以评价精密车削陶瓷表面质量并提高加工效率，刀具几何形状和进给量主要影响几何干涉粗糙度，工件力学性能、切削速度、切削深度和切削力主要影响脆性崩碎粗糙度。图5(a)所示为车削脆性材料过程中已加工表面形貌，图5(b)所示为车削过程中的表面形貌进给量提取图，显示了环形刀具刃口在工件基体上的复制效果。总体上，在车削过程中，可以将刀具对表面的复写归纳为如图5(c)所示。

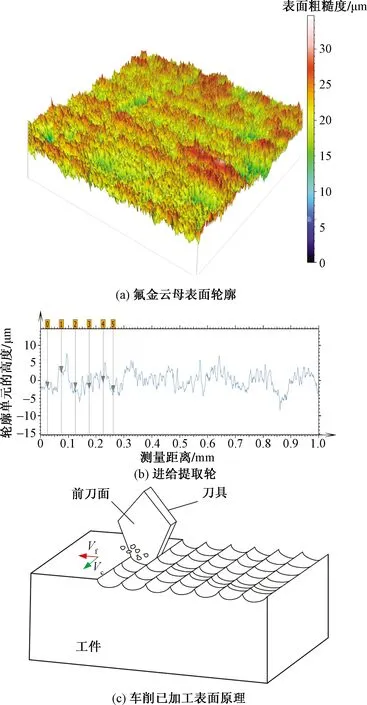
Vf为进给速度；Vc为切削速度

Kim等[39]研究了刀具与工件之间的振动对表面轮廓的影响，指出刀具振动在已加工表面留下凹槽，刀具振动频率与主轴转速频率之比的整数和分数决定了凹槽的数量、方向和间距。Sung等[40]使用亚像素边缘探测方法结合矩不变算子和改进的sobel 2-D滤波算子提取刀尖圆弧轮廓，将刀尖轮廓直接复写到工件轮廓上。分析了精车过程时刀尖轮廓公差对表面粗糙度的影响。发现尽管刀尖轮廓偏差在标准范围内，刀尖轮廓偏差对表面粗糙度有很大的影响。

此外，刀具磨损是车削中不可避免的影响表面粗糙度的因素之一，孔金星等[41]在微量润滑方式下进行涂层刀具的纯铁车削刀具磨损实验，得出随着刀具磨损的增加，表面呈现出不同程度的撕裂和破坏。马廉洁等[42]在进行车削玻璃陶瓷刀具磨损实验时，分别用5种不同刀具探讨刀具磨损量对加工表面粗糙度的影响，指出刀具磨损改变了刀尖部分的力学性能，使得陶瓷表面出现了很多的裂纹，随着刀具体积磨损量的增加，已加工表面伴随着大量凹坑的出现，已加工表面破坏严重。此外，得出聚晶金刚石(polycrystalline diamond，PCD)刀具是最适合车削玻璃陶瓷的材料。鲁康平[43]探讨了喷雾冷却的高速车削刀具磨损对表面粗糙度的影响。徐小磊[44]利用两种常用的陶瓷刀具Sialon陶瓷刀具和SiCw-Al2O3陶瓷刀具进行Inconel718表面粗糙度与刀具磨损研究，得出了车削Inconel718控制表面粗糙度的最佳陶瓷刀具材料，并分析了不同冷却介质下的刀具寿命。

2.3 工件材料对表面粗糙度的影响

在塑性切削过程中，由于刀具的切削刃钝圆半径的影响，材料某些部分会无法从工件本身脱落下来，造成刀具与工件无法正常切削，主要以滑擦为主，该层材料的厚度称为最小切削厚度hmin。此时由于后刀面会对未切削下来的材料进行剧烈挤压，致使部分材料产生塑性变形，加工完成以后工件材料出现弹性回弹；另一部分材料则在刀具切削刃的挤压下，发生侧向流动，这种因刀刃作用的材料侧向流动现象，称为塑性侧流。在脆性切削过程中，当切削深度到达某一临界值时，会产生脆性裂纹。脆性裂纹包含两个阶段，一是材料的弹性形变，二是材料的脆性断裂阶段。弹性回复和塑性侧流因素反映了刀具与工件材料相互作用对表面粗糙度的影响。

图6(a)展示了PCD刀具车削氟金云母时的材料变形示意图。不同于金属材料的塑性剪切去除机理，脆性材料切削层去除方式主要为断裂破碎。崩碎切屑的形成主要经历3个阶段[45]：裂纹形成、裂纹扩展和切屑断裂。由图6(a)可知，开始切削时，刀具与陶瓷工件发生尖锐的初次挤压，刀刃与陶瓷接触区域会产生一个不可逆的弹塑性变形区，弹塑性变形区内的原始缺陷在临界载荷下变得不稳定，将演化为侧向裂纹和中位裂纹。这一过程为裂纹形成过程。弹塑性变形区内材料的去除方式主要为塑性去除。但是，当刀具继续切削时，弹塑性变形区边缘的侧向裂纹会发生扩展，材料发生小规模脆性破碎，工件材料的周期性弹塑性变形和断裂破碎会在表面留下近似周期性的轮廓，经过上述变形过程后，表面粗糙度的形成完成。图6(b)为车削脆性材料过程中已加工表面残留有周期性的刀痕，这是材料塑性去除的典型特征。

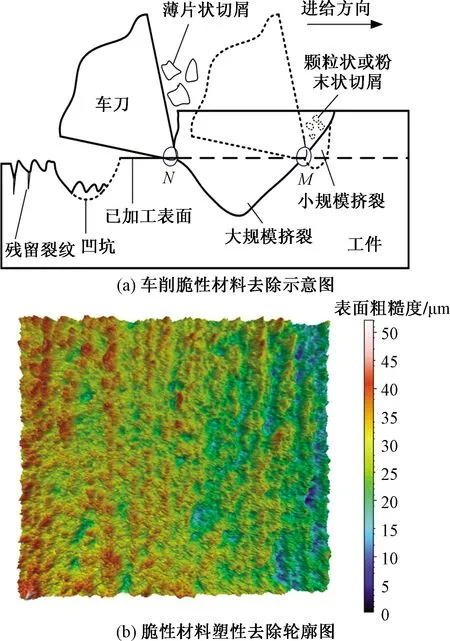
MN为凹坑之间的距离

Ma等[46]通过分析崩碎切屑的受力情况，根据脆性裂纹最大拉力扩展准则，提出脆性材料的凹坑倾斜角预测模型，随后，根据刀具与工件的干涉关系。建立了脆性材料车削表面的横向粗糙度Rat和纵向粗糙度Ral的预测模型。图7所示为表面粗糙度与切削速度的关系曲线。随着切削速度的增大，材料去除方式从韧性去除转变为脆性去除。在误差允许范围内与实验值吻合较好。

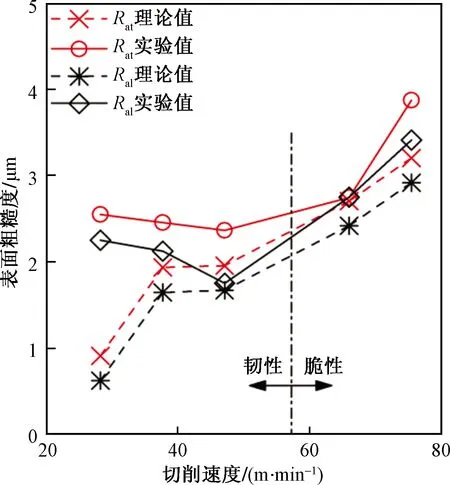
图7 表面粗糙度与切削速度的关系

在精密车削中，针对最小切削厚度及其对表面形成的影响，大量学者进行了研究。Zong等[47]基于运动学、最小未变形切屑厚度、加工后材料的塑性侧向流动和弹性恢复的影响，建立了一个单点金刚石精密车削表面粗糙度模型。并考虑了最大未变形切削厚度和切削刃钝圆半径的尺寸效应。Zhang等[48]建立了基于瑞利概率分布的未变形切屑厚度模型的表面粗糙度分析模型。He等[49]在此基础上又考虑了刀具刀尖轮廓的波纹度和车削过程中的随机因素，提出了一个新的表面粗糙度理论模型。Arif等[50]通过对单晶硅和BK7玻璃的加工试验，提出了一种基于特定切削能量的模型来预测韧脆转变的临界未变形切屑厚度。并根据未变形的切屑厚度确定了转换点，在该转换点处，能量模式经历了从基于塑性变形到基于断裂的转换。吴继华等[51]基于切削中切屑形成机理提出了最小切削厚度的预测模型，用非线性拟合的方法处理实验数据，发现切削厚度与进给量成指数关系。Liu等[52]阐述了预测hmin的理论模型。通过实验验证了模型的预测精度和有效性。

为了计算材料回弹，Arcona等[53-54]建立了刀具刃口半径和工件材料性能(如硬度和弹性模量)的经验模型。He等[55]进一步解释了工件的弹塑性特性是材料回弹的机理。To等[56]发现在加工过程中，由于工件材料的膨胀，刀具周边的轮廓会变形。因此，将材料回弹归因于工件材料的膨胀特性。

塑性侧流是表征材料属性的另外一个因素。在车削加工过程中，塑性测流同样对加工表面粗糙度有着一定的影响，Liu等[57]提出了一种考虑塑性侧流、刀具几何和工艺参数影响的Al5083-H116合金微车削表面粗糙度预测模型。该模型精确地估计了微米级变形下Al5083-H116的平均流动应力。结果表明，车削表面粗糙度理论值与实测值的差异主要是由于塑性侧流引起的表面粗糙化。此外，在低进给时粗糙度的增加可归因于直接在刀具前方的材料因应变梯度引起的强化而增加的侧流。Kishawy等[58]考察了刀尖半径、进给量和刀具磨损等工艺参数对材料塑性侧流的影响，结果显示刀尖半径的增加、刀具磨损的影响对塑性侧流的影响显著增加。Zong等[59]在考虑了加工材料的塑性侧流和弹性恢复后，建立了单点金刚石车削表面粗糙度的综合预测模型，预测和实验表明，由于金刚石的运动学、最小未变形的切屑厚度、塑性侧流和材料的弹性恢复对表面形成的竞争效应，金刚石表面粗糙度存在守恒定律。

根据上述结果，表2总结了预测最小未变形切屑厚度、材料回弹和塑性侧流的理论模型。

表2 最小未变形切屑厚度、材料回弹和塑性侧流理论模型

2.4 其他因素对表面粗糙度的影响

在车削中，表面粗糙度的形成还受环境因素的影响。Sreejith[60]研究了用金刚石涂层硬质合金刀具加工6061铝合金时，不同润滑环境的影响。分析了干切削、最小润滑油用量和冷却液条件对切削力、加工工件表面粗糙度和刀具磨损的影响。研究发现，最小润滑油用量工况效果最为明显。在切削过程中，刀具-工件接触区域温度升高将导致刀具变形，影响工件化学元素扩散速率，进而导致刀具磨损。刀具的变形和磨损最终恶化了表面粗糙度。马廉洁等[61]通过研究脆性材料车削中不同的温升阶段，根据切削系统热传导及热累积效应，建立了以刀具-工件接触点为热源的脆性材料切削热传导理论模型，结果表明，在脆性材料切削中，温度对表面的影响存在跃迁情况。同时机床的热效应会导致主轴变形，也会恶化车削表面粗糙度。

如上所述的工件材料和环境相关因素是车削中不可控制的参数[62]，因此，将这些参数划分为“复杂”的建模因素。虽然它们很难用定量的方法来表达，但仍有人试图克服建模的困难。例如，He等[63]提出了一种统计方法，即高斯分布，用来考虑这些因素的影响，预测了金刚石车削表面粗糙度的上下限。今后这些不可控因素的内在机理需进一步阐明。

3 表面粗糙度理论建模研究展望

理论建模方法预测切削表面粗糙度是一项复杂的工作，但它对了解切削表面形成破坏机理和获得满意的表面完整性具有重要意义。目前很多学者已经较全面地将这些影响因素纳入表面粗糙度理论模型中，但由于对这些影响因素的内在机理认识不足，仍有许多工作要做。在总结前人工作的基础上，对车削表面粗糙度理论建模的不足做如下总结。

首先，根据切削粗糙度理论建模影响模式，将“复杂”建模因素分为两类，分别是确定性因素和不确定性因素。确定性因素包括切削速度、进给量、切削深度、刀具和工件材料属性。在一般车削中，切削深度和切削速度是构成表面粗糙度的两大关键因素，它影响了刀具-工件接触区域的切屑成形情况，改变了材料的变形率。进给量是影响表面粗糙度的最大因素，进给量的大小会影响已加工表面的峰谷间距。切削三要素目前已经较多的被考虑到车削表面粗糙度理论建模中。无论在塑性去除还是脆性去除中，一般应用Johnson-Cook方程，综合到表面粗糙度的理论模型中来反映其影响。

第二，不确定性因素包括材料的晶界、晶体结构和排布，以及试验过程中的冷却液和杂质共同随机影响表面粗糙度的形成。目前针对车削过程中的不确定因素研究较少，所以应对不确定因素的影响加以阐述，随机分布、概率统计与神经网络的方法对研究随机性的影响比较突出。适合用来针对随机性建模。

第三，在塑性车削表面粗糙度的理论模型主要考虑空间尺寸影响，但脆性粗糙度模型中对于考虑三维尺寸影响因素较少，同时二者忽略了时间维度的影响因素。例如，在车削理论模型中，没有考虑刀具磨损对表面粗糙度的完善体系。然而，随着刀具在切削过程中的累积磨损，会对表面有着不同程度的破坏。例如塑性去除的积屑瘤，脆性去除中的刀具磨损面形貌和刀具形成的切屑。因此，时间维度对表面粗糙度的影响有待进一步研究。

第四，在微尺度车削过程中，会忽略掉一些实际影响因素而往往以理想化车削建模。例如材料去除中的塑性侧流和回弹现象以及脆性去除的实际已加工表面形貌，在这种情况下，可以通过全面了解内在材料破坏机理和影响因素的内在机制，引入一些修正因子来定义并校准这些因素。