哈萨克羊×特克赛尔羊杂交F1代体尺与体重的相关及回归分析
2021-08-19刘宜勇刘建明褚洪忠陈春华杨光维张志东吐来力江邱梅玉
张 梅,李 涛,刘宜勇,*,刘建明,褚洪忠,陈春华,杨光维,张志东,团 勇,吐来力江,邱梅玉
(1.伊犁职业技术学院,新疆 伊宁835000;2.伊犁州畜牧科学研究所;3.新疆畜牧科学院生物技术研究所)
哈萨克羊是我国肉羊养殖的重要畜禽遗传资源,通过新疆科技育种者的精心选育,形成了现在的超强适应性和抗逆性以及幼畜早期发育性能强等遗传特点,但存在繁殖率较低、尾脂过多、体躯浅且前胸狭窄等缺点。特克塞尔羊具有高产羔率,发育潜能高、母羊性成熟较早,产肉率和产毛率较高等特点,是肉羊经济杂交改良的优质父本。为改善哈萨克羊繁育中存在的以上缺陷,利用特克赛尔羊的优良基因进行杂交改良,从而提高个体生产性能以及牧民养殖经济效益。特哈杂交改良是以外引荷兰特克赛尔公羊作为父本,当地哈萨克羊为母本的杂交选育工作,杂交后代结合了哈萨克羊的强抗逆性和强适应性以及特克赛尔羊繁殖率高、产肉率高等特点。
通过对体尺、体重的测量和研究,我们可以直观的了解到畜禽体格发育和体躯结构变化,对杂交改良选育有着重要的指导意义。国内外学者对此做了很多研究,如Doeschl、徐宁迎等通过对猪屠宰后与产肉率相关的各项指标进行了评估,进而建立了最优回归方程,为品种选育提供了有效方法。因此通过体尺性状的分析可间接选育出繁殖性能好、适应性及抗病力强的优质种质资源。近年来各国科技工作者对哈萨克羊的选育做了大量工作,而在特哈杂交后代体尺和体重的相关及回归分析的文章却相对较少。试验旨在探究特哈杂交F1代6月龄羔羊体尺和体重的相关及回归分析,筛选并建立其最佳回归方程并用于实际生产,为特哈杂交优质后代的培育提供科学理论指导。
1 材料与方法
1.1 试验动物
试验选取昭苏马场和伊犁种马场哈萨克羊×特克赛尔羊杂交F1代368只,公羔184只,母羔174,体况发育健康的6月龄羔羊为试验样本。
1.2 测定指标及测定方法
参考赵有璋《羊生产学》中的测定方法对每只羔羊的体重(Y),体高(X1)、体斜长(X2)、胸围(X3)、胸宽(X4)、胸深(X5)、管围(X6)进行测定;体重用电子秤称量;通过测杖测定体斜长、体高、胸深、胸宽;胸围和管围用卷尺测量。
1.3 数据处理
首先将原始数据在Excle文件中进行归纳整理,剔除无效和错误数据。再用 SPSS19.0对体重和体尺数据进行相关分析和逐步线性回归分析,进而筛选建立体重和体尺性状间的最佳回归方程。
2 结果
2.1 体重和体尺指标的表型分析
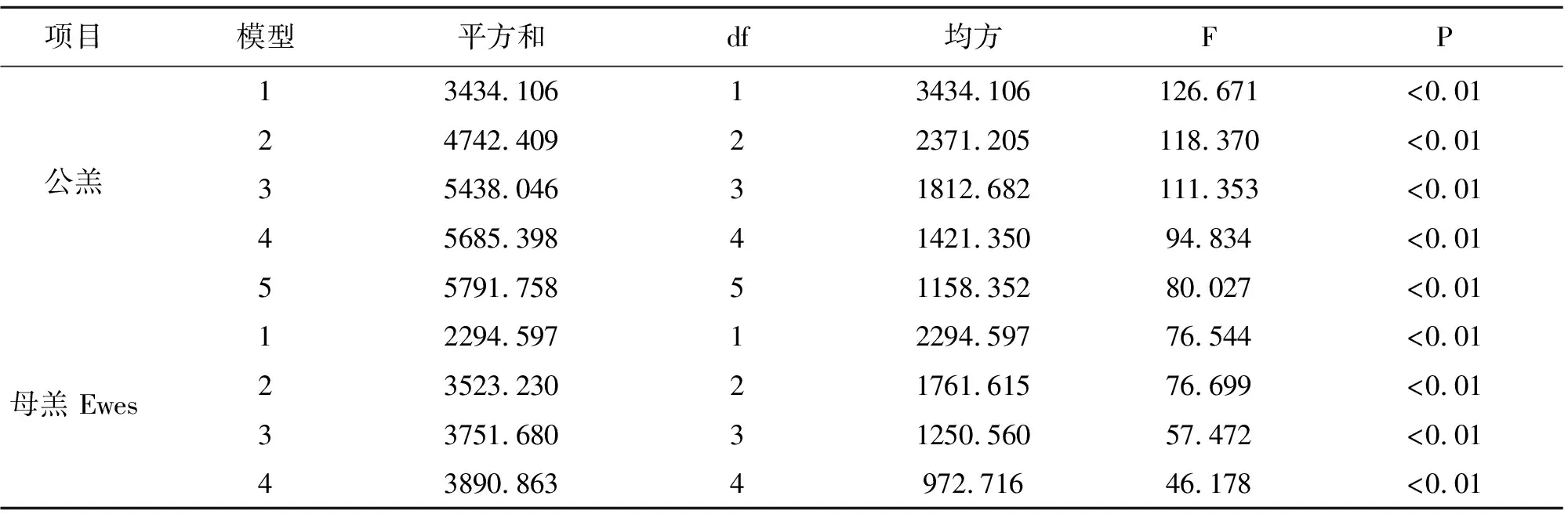
通过表1我们可以发现,与母羔相比,F1代公羔的X1极显著较低(P<0.01),同时公羔的X5、X4、X2、X6、X3的均值极显著低于母羔(P<0.01)。CV最大的为Y,公羔CV为15.87%,母羔的CV为16.61%,处于中等变异水平(10% 表1 体重与体尺性状的平均数、标准差及变异系数 通过2、3我们可以发现,不管是公羔或者母羔,其F1代的Y与各项体尺性状间均表现出极显著的相关性(P<0.01),公羔的相关程度由大到小为:X2(0.641)>X3(0.623)>X1(0.594)>X6(0.486)>X5(0.416)>X4(0.397);母羔相关程度由大到小为:X2(0.555)>X5(0.549)>X1(0.538)>X3(0.510)>X4(0.464)>X6(0.429)。除公羔X4和X5两项体尺指标与X3没有显著的相关性外(P>0.05),公羔和母羔的其它各项体尺指标之间均表现为极显著的正相关性(P<0.01),其中公羔X1和X5的相关性最高(为0.568),母羔的X1与X2相关性最高(为0.617)。公羔的X6与X5相关性性表现为最低(为0.236),母羔X4与X1的相关性最低(0.225)。 表2 公羔体重和体尺指标的相关性分析 表3 母羔体重和体尺指标的相关性分析 通过表4我们可以看出,对公羔Y的直接作用效果最大的是X3(为0.359),对Y直接作用效果最小是X5(为0.038),对Y的间接作用效果最高的是X5(为0.380),对Y的间接作用效果最低的是X6(为0.241),对公羔Y的直接作用效果表现为X5 表4 公羔体重和体尺指标的通径分析及相关系数分解 表5 母羔体重和体尺指标的通径分析及相关系数分解 通过表6、表7可以得出,公羔体重和各性状间的最佳多元回归方程为Y=-74.203+0.291X2+0.350X3+0.504X1+0.515X4+1.446X6(模型5),标准化后的多元方程为Y=-74.203+0.272X2+0.357X3+0.285X1+0.159X4+0.129X6,复相关系数r=0.832,P<0.01,可决系数R2=0.692;母羔体重与各性状间的最佳多元回归方程为Y=-59.179+0.406X2+1.152 X5+0.753X4+0.369X1(模型4),标准化后的多元方程为Y=-59.179+0.295X2+0.296X5+0.209 X4+0.184 X1,复相关系数r=0.723,P<0.01,可决系数R2=0.522。公、母羔的方差分析的F值分别为80.027和46.178,概率P<0.01(表8)。 表6 体重和体尺指标的逐步回归模型 表7 体重和体尺指标多元回归系数的参数估计值 续表7 体重和体尺指标多元回归系数的参数估计值 表8 体重和体尺指标多元回归方差分析 体重和体尺作为评价个体生长发育的无损指标,不仅能反映出个体自身发育情况,也与个体的生产性能息息相关。本试验通过对特哈F1代羔羊体重与体尺的相关及回归分析建立最佳方程,在生产实际中对改善养殖环境,增加养殖收入和选育优秀个体具有深远的意义。本试验表型分析揭示了公、母羔体重的CV均高于10%,而体尺的CV均低于10%,说明特哈F1代体重有着较高的选育潜能,而体尺的选育潜力则较低。 利用各体尺的表型进行相关性分析,我们可以发现体尺对体重的综合作用效果。本研究结果分析发现,母羔各体尺间均表现出极显著的相关性,公羔除胸围和胸宽与胸深没有明显的相关性外,其它各指标间均表现出极显著的相关性,这与田亚磊等研究有着相似的结果。Sowande等研究结果说明体尺性状三项指标与体重的相关性最高,王志明、裴杰等研究结果与其一致。本研究结果表明体斜长与体重的相关性最高,为0.641和0.555,说明体斜长对体重的直接综合作用最大,与Sowande等结果存在差异,推测出现不一致的原因可能是由于品种、饲养、管理等多种因素引起的,这些都有待进一步研究证实。 利用通径分析我们可以了解两个变量之间的相互作用,从而反映出二者之间的相关性,从而得出相关回归系数。本研究结果表明,公、母羔的胸围、体高、胸深、体斜长对体重的综合作用效果显著,但对体重的直接作用效果较低,间接作用对体重的影响较为显著,对公、母羔间接作用效果最高的是胸围与胸深,最小的为管围和胸深。可以发现各项体尺性状是通过直接作用和间接作用效果相结合来影响个体生长发育的。综上可以发现影响体重的因素和途径较多,所以在实际选育过程中要综合考虑多种因素的影响,在品种选育时可结合本试验筛选建立的最佳多元回归模型进行科学选育。 通过对各体尺性状与体重的逐步回归分析,从而得出最优多元回归方程,进而准确评估体尺性状对体重的作用效果。本试验将体尺性状逐步纳入回归方程中,通过逐步多元线性回归分析筛选建立公羔体尺与体重的最佳方程Y=-74.203+0.291X2+0.350X3+0.504X1+0.515X4+1.446X6,将上述回归方程标准化后得到Y=-74.203+0.272X2+0.357X3+0.285X1+0.159X4+0.129X6,母羔体尺最佳回归方程为Y=-59.179+0.406X2+1.152X5+0.753X4+0.369X1,将上述回归方程标准化后得到Y=-59.179+0.295X2+0.296 X5+0.209X4+0.184X1,两个最佳回归方程都纳入了体高、体斜长和胸宽三个性状。王伟峰通过线性回归分析建立的最佳回归方程中纳入了体斜长和胸围两个体尺性状;王红军通过逐步回归分析建立的最佳回归方程中纳入了体斜长和胸围两个体尺性状,上述研究结果与本试验研究结果相似。而李胜开、热西提等相关逐步线性回归将体高、体长、胸围3个体尺性状纳入了其建立的最佳回归方程中;沂蒙黑山羊的逐步线性回归分析将胸深、管围和胸围3个体尺性状纳入了其建立的最佳回归方程中。以上研究结果与本试验结果中存在不一致的地方,分析导致上述结果的原因可能是当地的饲养环境和管理水平等多种非遗传因素有关。 公羔、母羔的线性方程决定系数R2分别为0.692和0.522。说明纳入回归方程的体尺性状对羔羊的体重有明显的影响作用,1-R2分别为0.308和0.478,说明还有尚未选入影响体重的因素,因此影响特哈杂交F1羔羊体重的因素还需作进一步研究探讨。 特哈杂交F1代各项体尺性状与体重间都表现出极显著的相关性,各体尺性状间除公羔胸宽与胸围两项体尺性状与胸深没有显著的相关性外,其它各体尺性状之间都表现出明显的相关性,其中体斜长与体重的相关性表现为最高。对体重的直接作用最为明显的是胸深和胸围两项体尺性状,对体重的间接作用最为明显的是体斜长、体高、管围和胸宽4个性状。6月龄公羔的最佳线性回归方程为Y=-74.203+0.272X2+0.357X3+0.285X1+0.159X4+0.129X6,(r=0.832,P<0.01)、6月龄母羔的最佳多元回归方程为Y=-59.179+0.295X2+0.296 X5+0.209 X4+0.184 X1,(r=0.723,P<0.01)。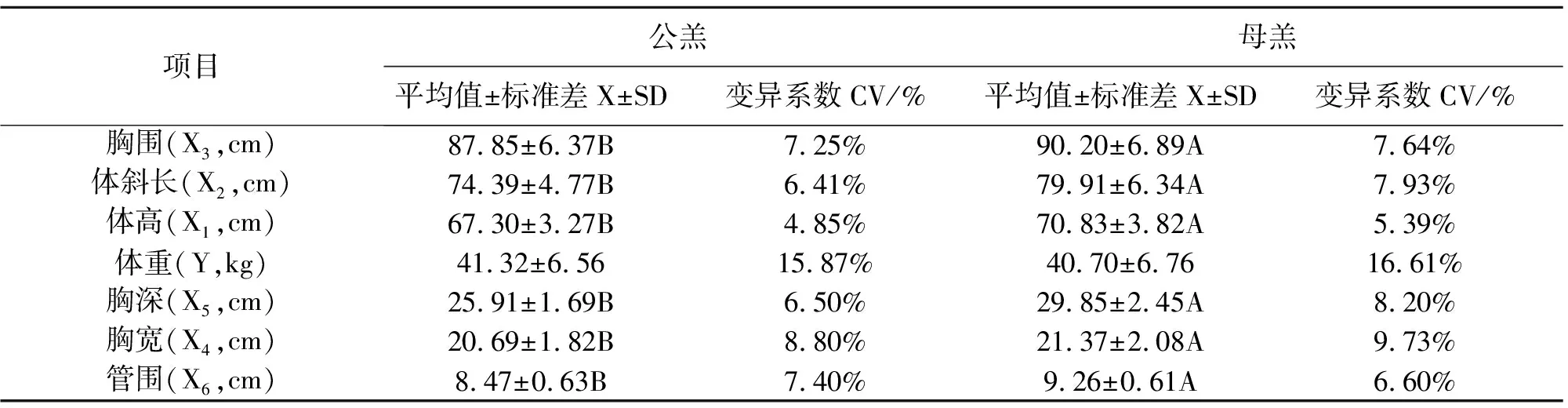
2.2 体重和体尺指标的相关性分析
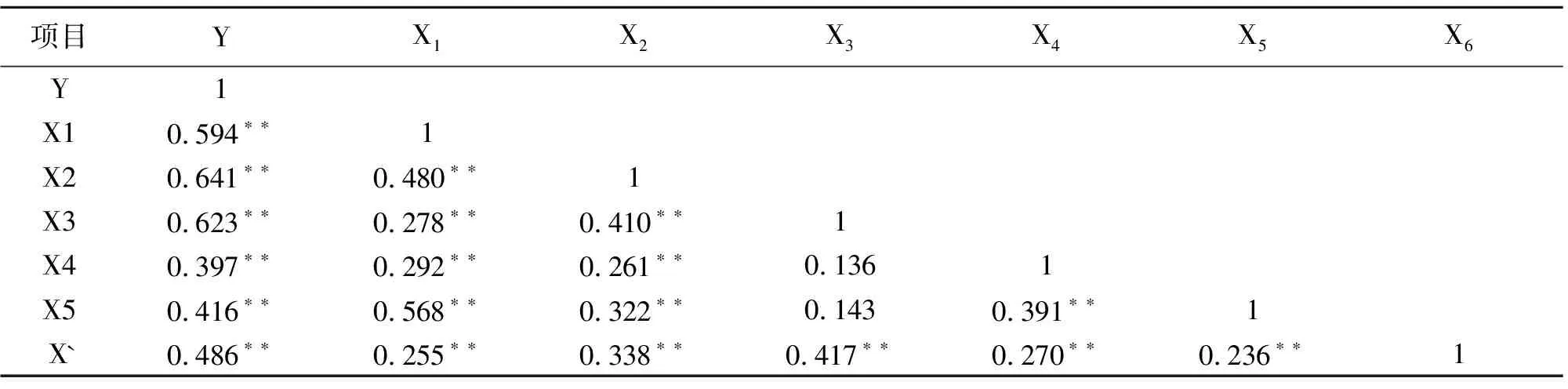

2.3 体重和体尺指标的通径分析及相关系数分解
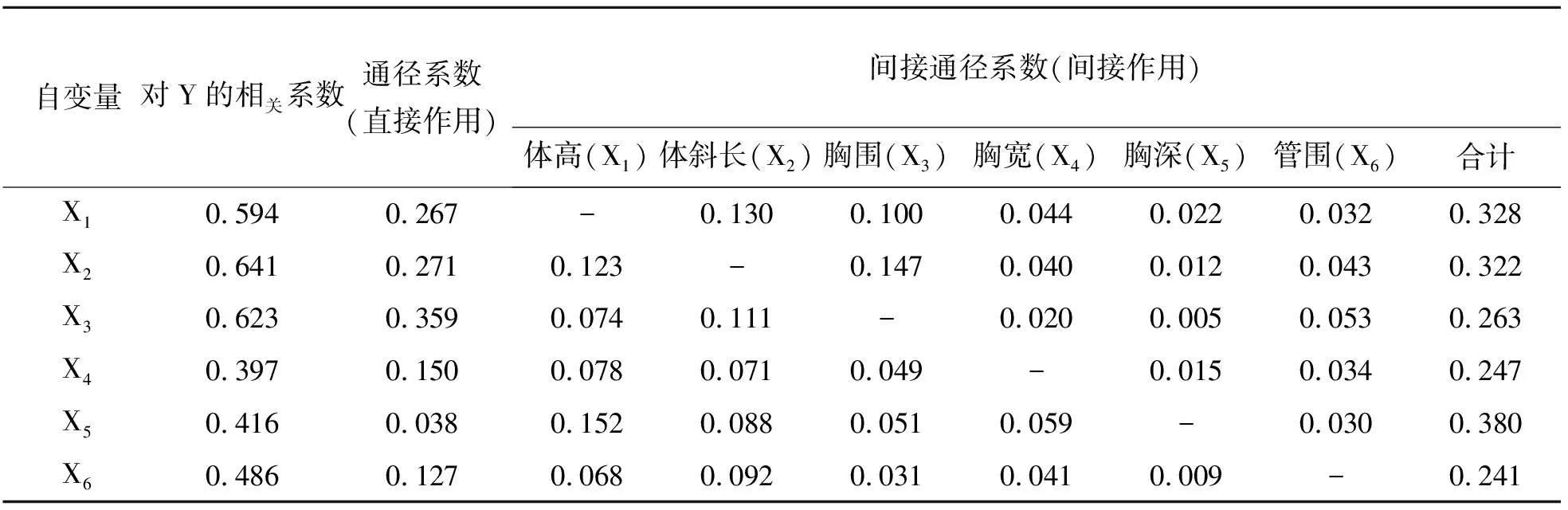

2.4 体尺指标对体重和逐步回归分析
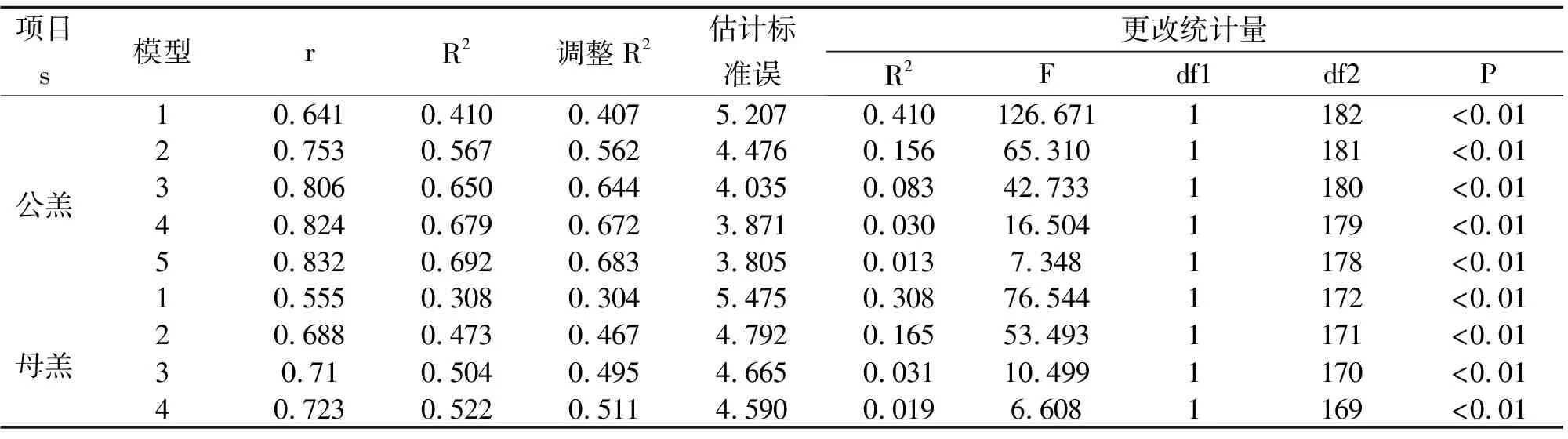


3 讨论
3.1 体重和体尺指标的表型分析
3.2 体重和体尺指标的相关性分析
3.3 体重和体尺指标的通径分析及相关系数分解
3.4 体尺指标对体重逐步回归分析
4 结论
