领悟方法本质 淡化解题技巧——例谈抽象函数单调性问题中的移项赋值构造与添项赋值构造策略

邹景斌 朱贤良

(1.安徽省铜陵市第三中学 244000;2.安徽省枞阳县宏实中学 246700)

波利亚有一句名言：“掌握数学就是意味着善于解题.”解题，是数学教学中必不可少的一个环节.在解题教学中，有些教师或是参考答案常用一些奇思妙想的高招，却忽略了最本质、最常用的通法，使得学生在击掌赞叹的同时，只能望而长叹：为啥我就没想到？教学实践表明，用一些看似高明却极其不自然的技巧让学生眼花缭乱，又或者用极其复杂的思路与方法让学生晕头转向，这些低效或无效的解题教学只能感叹数学看上去很美，导致学生在解题的百转千回中迷失方向.

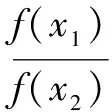
一、移项赋值构造策略

类型1f(x·y)=f(x)+f(y)型

例1 已知函数f(x)的定义域是(0，+∞)，当x>1时，f(x)>0，且f(x·y)=f(x)+f(y).试判断f(x)在定义域上的单调性.

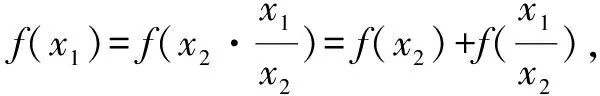
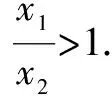
评注这里将f(x·y)=f(x)+f(y)移项成f(x·y)-f(x)=f(y)，从而赋值构造得到差式f(x1)-f(x2)，一目了然.这样的解法洞悉了问题的本质，一步到位.在实际教学中，笔者采用此法取得了良好的效果.

类型2f(x+y)=f(x)+f(y)型

例2设函数f(x)定义域为R，且对任意x,y∈R，都有f(x+y)=f(x)+f(y)，当x>0时有f(x)>0.试判断f(x)的单调性.

参考解法(拆分构造差式)不妨设x1,x2∈R且x1>x2，则x1-x2>0，且f(x1-x2)>0.

由f(x+y)=f(x)+f(y)可得f(x1)=f[x2+(x1-x2)]=f(x2)+f(x1-x2)，则f(x1)-f(x2)=f(x1-x2)>0，即f(x1)>f(x2)，故f(x)在R上是增函数.

评注这里的难点是对f(x1)进行拆分：f(x1)=f[x2+(x1-x2)]=f(x2)+f(x1-x2)，学生难以理解这种拆分构造，容易与例1混为一谈、乱成一团.

评注移项赋值构造策略在求解例1与例2时保持了一致，学生不需要去区分这两种类型，从而使解法得到统一.学生一看就明白如何构造差式f(x1)-f(x2)并判定其正负情况，一点就通.

类型3f(x+y)=f(x)+f(y)+k型

二、添项赋值构造策略

类型4f(x+y)=f(x)·f(y)型

例4 定义在R上的函数y=f(x)，满足f(x)>0，当x>0时，f(x)>1，且对任意x,y∈R，都有f(x+y)=f(x)·f(y).试判断f(x)在R上的单调性.

参考解法1(拆分构造差式)设任意x1,x2∈R且x1>x2，则f(x2)>0，且x1-x2>0，f(x1-x2)>1，故拆分可得f(x1)=f[x2+(x1-x2)]=f(x2)·f(x1-x2)，从而构造差式f(x1)-f(x2)=f(x2)·[f(x1-x2)-1]>0，即f(x1)>f(x2)，所以f(x)在R上是增函数.

评注解法1采用作差比较，解法2采用作商比较，两种解法在本质上是一致的.与前面的例题一样，难点仍然在于拆分变形“f(x1)=f[x2+(x1-x2)]=f(x2)·f(x1-x2)”.以下我们再采用更为自然、合理的移项赋值构造与添项赋值构造策略来进行解题.

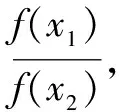
类型5f(x·y)=f(x)·f(y)型

例5已知函数f(x)对任何正实数x,y都有f(x·y)=f(x)·f(y)，且f(x)≠0，当x>1时，f(x)<1.试判断f(x)在(0，+∞)上的单调性.

上述五种类型的抽象函数单调性问题，在使用拆分构造策略进行求解时，技巧性较强，学生常有神来之笔的感觉，故而难以理解，解题极易犯迷糊.这种不自然、不合理的思路也常让教师犯难，难以讲得清楚明白，因为教师不仅要讲清楚怎样变形，更要讲清楚为什么要这样变形.移项赋值构造与添项赋值构造策略很好地解决了这个问题，直截了当地通过移项赋值与添项赋值得到差式或商式，其求解思路与学生的思维方式相符，学生易学易懂.基于这样的认识，笔者认为，无论是教师的教，还是学生的学，都要领悟方法的本质，研究透彻，从而淡化解题技巧，践行大道至简的初心.