基于融合解析迭代重建网络的高效稀疏投影CT重建算法

陈高宇， 黄 秋

(上海交通大学 生物医学工程学院， 上海 200240)

0 引言

受到扫描协议或者成像系统硬件的影响，一方面，稀疏投影重建问题在能谱CT[1-2]、牙科锥束CT[3]、四维锥束CT[4]等场景中十分常见；另一方面，减少CT扫描过程中投影角度的数量可以降低病人所受的辐射剂量。但是，投影角度减少会导致重建图像产生严重条状伪影。传统稀疏投影重建算法通过投影补全[5-6]、压缩感知[7-9]等方法来减少条状伪影，提高重建图像质量。近年来深度学习技术[10-11]被广泛研究并应用于CT图像重建领域，在稀疏投影重建[12-18]等任务上展现出了很大潜力，在高倍数稀疏情况下的重建性能优于传统算法。在之前的工作中，我们提出了一种融合解析迭代重建网络(fused analytical iterative reconstruction networks, AirNet)[19]，在稀疏角、有限角等稀疏投影数据上得到了高质量的图像。

AirNet是一种结合传统融合解析迭代重建模型AIR[20]与深度卷积神经网络的CT重建模型，可以表示为以下的两步迭代式：

(1)

式中，第一步为控制数据一致性的保真更新过程，包含了前向投影和滤波反投影过程；第二步则是使用卷积神经网络实现的正则化过程。式(1)中的x为迭代图像，A和F为投影算符和滤波反投影算符，s为可训练的步长因子。在第二步中，AirNet使用了残差连接和密集连接策略来增强特征信息在网络前后层之间的传输能力，降低网络训练难度，提高最终重建性能。其中的密集连接将前期迭代中间图像作为特征图拼接到一起作为当前迭代的网络输入，CNN(,θ)为卷积神经网络，其输入为[xn-1/2,xn-3/2,…,xn-m+1/2],n为迭代编号,m为密集连接数。

图1所示为AirNet中每次迭代默认使用三层卷积神经网络结构，卷积层(Conv)和激活函数(ReLU)交替排列。每次迭代中xn-1/2和xn的残差连接，配合整体50次迭代构成了很深的残差网络。由于AirNet使用了数十次迭代，每次迭代中的投影反投影过程会耗费大量计算时间。同时多次迭代还会带来网络参数量的提升，增加模型的显存占用。若直接减少模型的迭代次数，网络参数量减少，表达能力会下降，导致模型的性能下降[12,19]。本文在实验中发现AirNet中投影和反投影计算部分对显存和计算时间的影响比卷积神经网络部分更大，因此，考虑通过增加单次迭代中的卷积神经网络层数来保持网络的表达能力。然而，当单次迭代中网络层数增加到一定程度之后，网络的训练难度也会增加，导致模型性能下降[12]。

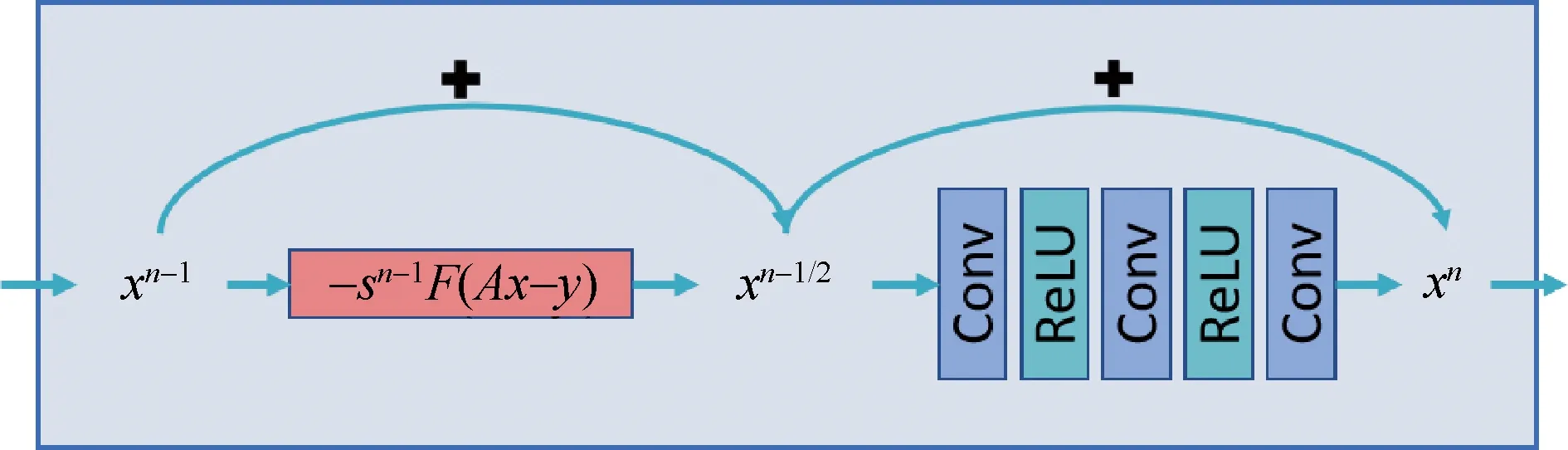
图1 AirNet模型中单次迭代的结构，省略了迭代间的密集连接

为了解决上述问题，本文在AirNet基础上提出了两种新的迭代残差连接形式：迭代内连接和迭代间连接。两种新结构在减少迭代次数，增加每次迭代的网络层数的情况下，通过提高特征信息的传输能力来保持模型的性能，并且能够有效降低显存占用，提高重建速度。

1 模型与方法

1.1 迭代残差结构

1.1.1 迭代图连接

首先考虑在原始AirNet上直接增加单次迭代中卷积层数的情况，图2(a)所示为一个8层卷积神经网络结构。其中黄色方块所代表的隐藏层h依序串联，原始AirNet只在重建图x之间存在残差连接。本文称图2 (a)中青色箭头表示的连接xn-1/2到xn的残差连接结构为迭代图连接，代表连接迭代过程中单通道的中间图像。当单次迭代中网络层数较大，xn-1/2到xn之间就形成了一个较深的卷积神经网络。基于ResNet[21]的研究结果，如此深层的卷积神经网络较难训练，可以通过残差连接来降低训练难度。由于x为单通道重建图，h为多通道特征图，无法在两者之间建立直接的残差连接，因此，可以考虑建立隐藏层之间的残差连接。

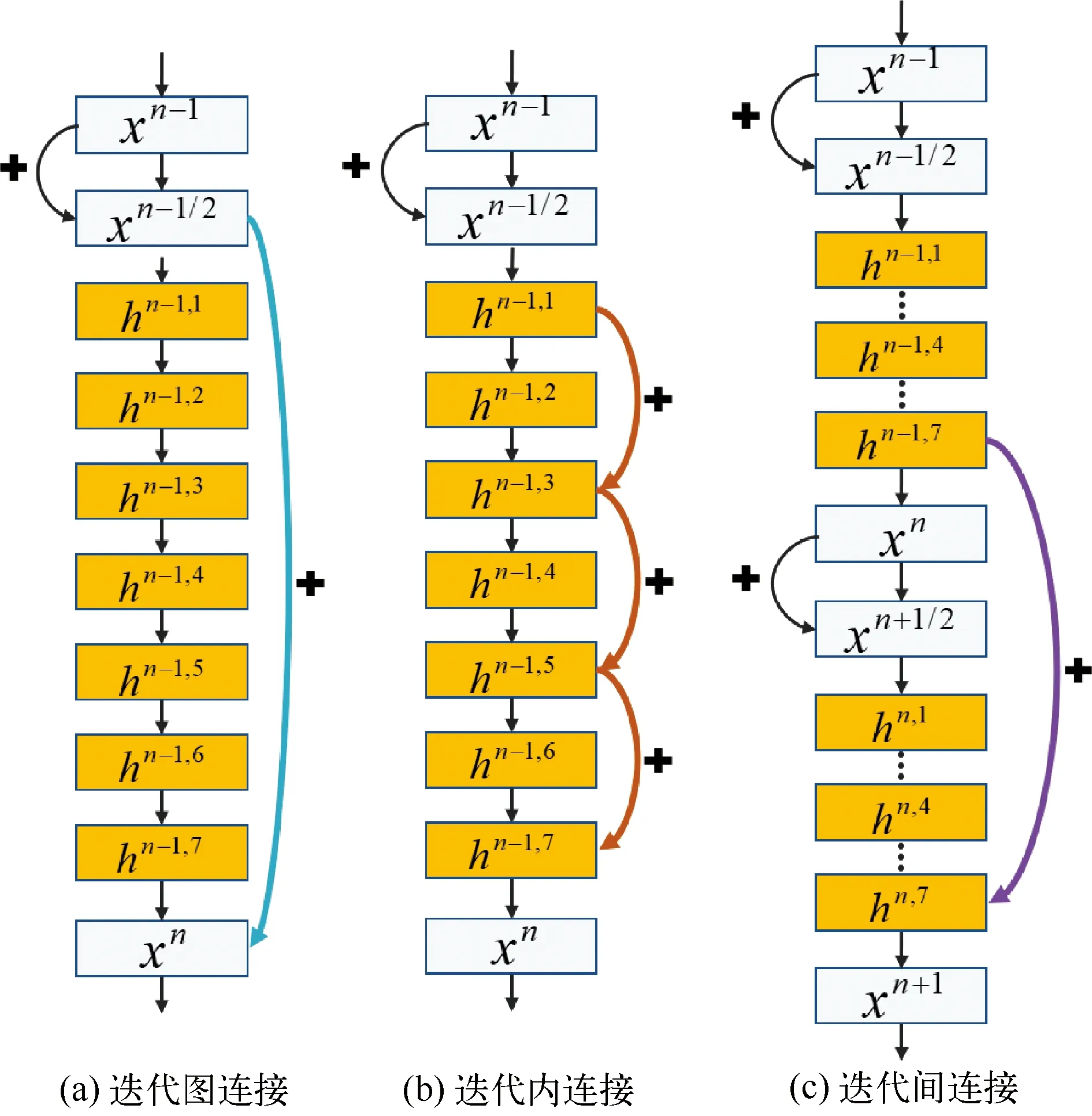
图2 三种不同迭代残差结构

1.1.2 迭代内连接

为了充分利用残差学习的特性降低网络训练的难度，本文首先考虑在AirNet迭代内部建立隐藏层的残差连接。其连接结构如图2 (b)中跨层连接隐藏层hn-1,1、hn-1,3、hn-1,5和hn-1,7的三个褐色箭头所示，本文称之为迭代内连接。在单次迭代中卷积层数较多时，一方面，迭代内残差连接可以有效地建立起网络前后层之间的直接通路，使前向特征信息与反向梯度信息的传输更加高效，从而降低网络训练难度，有助于提高最终网络性能；另一方面，因为隐藏层h的通道数比中间图像x多，更有利于特征信息的表达和传递。当和迭代图连接使用同等数量的隐藏层时，迭代内连接并不会增加参数量。

1.1.3 迭代间连接

除了迭代内连接，还可以考虑迭代间的残差连接。图2 (c)中的紫色箭头将两个相邻迭代的最后一个隐藏层通过残差结构相连，实现了迭代间特征的跨层传输。此网络设计与循环神经网络[10]结构类似。将迭代间连接中的xn同时看作当前的输出和下一时刻的输入，通过隐藏层的连接建立两个相邻迭代之间的特征信息连接。不同的是，各迭代之间参数并未进行共享，隐藏层的连接也是通过残差而不是权重层。

本文中考虑这种残差连接方式有两个原因：第一是隐藏层具有比迭代中间图像更多的通道数，更有利于特征信息传递；第二是最后一个隐藏层被认为具有较为相似的特征。在传统迭代重建算法中，重建图像随着迭代过程逐渐收敛到最终解。与之类似的，本文认为AirNet的迭代中间输出图像xn随着迭代层数变深，将越来越接近最终的目标图像。因此，各次迭代中最后一个隐藏层应该具有相似的特征，连接两次迭代中的最后一个隐藏层比较符合传统迭代模型的特性。

1.2 卷积层初始化

本文还对AirNet中卷积层的初始化方式进行了实验性研究。深度神经网络中的参数初始化对模型的收敛速度和模型性能有非常重要的影响[22-23]。原始AirNet沿用了LEARN[12]中的初始化方式。对各卷积层中的权重参数做了高斯随机初始化，其高斯分布均值为0，方差为0.01。同时将偏置参数统一初始化为0。其中的超参数如高斯分布的均值和方差的选择是一个难题。深度学习技术领域经过长期的发展，已经发展出了一系列高效的通用参数初始化方式。例如Xavier Initialization[22]和Kaiming Initialization[23]两种初始化方式的提出就是为了令信号强度在神经网络训练过程中保持不变的前提下确定随机化超参数。使用此类初始化方式在通常的深度神经网络中往往可以获得比普通随机初始化更好的效果。

但是AirNet不同于常规的神经网络，其结构更加类似于传统迭代重建模型。为了研究初始化方式对于AirNet的影响，本章将Kaiming Initialization与AirNet原始的初始化方法进行了对比实验, Kaiming Initialization对于卷积层中权重参数使用均匀分布随机初始化U(-bound,bound)，其中bound为：

(2)

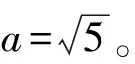
本文对于偏置参数的初始化也使用了均匀分布，其均匀分布超参数为:

(3)

为了方便表示，接下来的内容将原始AirNet的初始化方式记为G-Z，将Kaiming Initialization记为H-U。

1.3 加权损失函数

GoogLeNet[24]中通过辅助网络处理浅层的特征，将多级输出与标签之间的误差加权作为最终的损失函数。此结构有助于梯度回传到浅层网络，发挥正则化作用并避免梯度消失。但这种方法对模型性能的提升十分有限[24]。

GoogLeNet的网络结构从始至终都是一个特征提取的过程。随着网络层数加深，模型所提取的特征越来越高层，很难从浅层特征中通过一个辅助分类器获取可以用于最终分类的有效信息。本文认为这是该方案在分类任务上作用不明显的一个重要原因。相反，AirNet内部包含迭代形式，每步迭代都会产生迭代中间图像，中间图像与最终目标之间的关联性很强。在传统迭代重建模型中，迭代结果随着迭代进行将逐渐收敛至目标结果。因此，本文利用了此特性，借鉴GoogLeNet中的损失函数形式，将多层的迭代中间图像与标签图像之间的误差进行加权，构造了一种加权损失函数来降低深层卷积网络的训练难度。加权损失函数的形式如下：

(4)

式中，x*和xn分别为标签图像和模型第n次迭代的输出图像；a为一个常数。本文从最后一次迭代输出向前以等比形式逐渐缩小其在损失函数中的权重因子。最终迭代输出的权重为1，倒数第二次迭代为1/a，以此类推到第一次迭代输出。本文实验中常数a实验性地设为2。

2 实验设计

本文分别在仿真数据集和临床数据集上进行了对比实验，通过均方误差(mean square error，MSE)、峰值信噪比(peak signal to noise ratio，PSNR)和结构化相似度指标(structural similarity index measure，SSIM)[25]来评估不同算法的性能。其中仿真实验部分比较了使用不同迭代残差结构的AirNet的性能和效率，首先分别在50次和10次迭代情况下比较了模型的性能。其中50次迭代情况下每个迭代中包含2个隐藏层连接，10次迭代情况下则包含10个隐藏层连接。这样的设计使得50次迭代和10次迭代情况下的网络参数量保持在同等水平。为了验证新算法对于提高效率的作用，本文还对比了10次迭代的两种新结构(迭代内和迭代间连接)与50次迭代的原始AirNet结构(迭代图连接)的图像质量，显存占用和重建时间。临床实验部分则进一步将上述10次迭代的Efficient-AirNet与50次迭代的原始AirNet[19]、AIR-TV[20]，FBPConvNet[13]在图像质量和模型效率上进行了比较。本文中的所有深度模型均使用MSE作为损失函数。

2.1 仿真数据

本文使用20倍稀疏角(等角度区间)降采样的前列腺CT数据进行对比实验，该数据只包含20个投影角度，可以降低投影和反投影计算量，减少训练时间。训练集包含350张来自70个样本的尺寸为256×256大小的标签图像和投影数据，验证集50张，测试集100张。其探测器参数设置如表1所示。仿真数据上的训练周期为300个epoch，批尺寸为1，学习率从0.0001每10个epoch等比衰减一次，直到最终变为0.000 01。

2.2 临床数据

本文的临床数据来自于埃莫里大学医院87例CT扫描投影数据，其扫描部位涉及胸部和腹部区域。临床探测器的几何参数如表1所示。

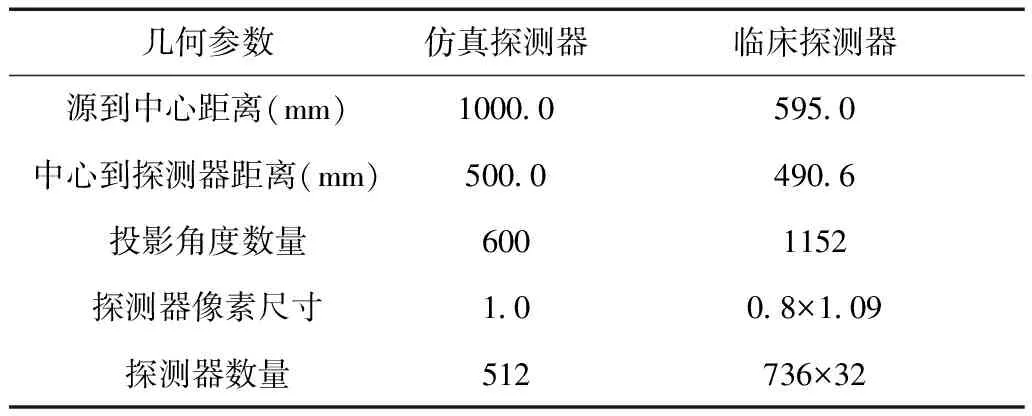
表1 CT探测器几何参数

本文使用的临床数据只包含原始投影数据y。为了获取作为标签的重建图像，首先使用AIR方法重建完整投影数据:

x*=AIR(y)

(5)

然后对投影数据y直接进行降采样获得相应的稀疏投影数据:

ysparse=DownSample(y)

(6)

投影数据ysparse包含了72个角度的投影数据，即16倍稀疏角降采样。由此获得的数据集(x*,ysparse)被用于各种重建方法的对比评估。本文将87个临床样本随机分成了60例、10例和17例，分别作为训练集、验证集和测试集。根据AirNet在仿真数据中对数据量的要求，本文从每例数据中沿轴向随机选择了6张图像用于实验。

本文在临床数据上对比了AIR-TV[20]、FBPConvNet[13]、迭代图AirNet[19]、迭代内AirNet以及迭代间AirNet的重建结果。其中AIR-TV为传统压缩感知类迭代重建算法；FBPConvNet为基于后处理的深度学习算法。对于AIR-TV算法，其外层迭代次数为50，内层正则迭代次数为100，各超参数分别为s=0.05，λ=0.004，μ=1.0。其余深度重建模型的训练周期均为100，学习率从0.001按每10个epoch逐渐下降至0.0001。

3 结果评估

3.1 50次迭代情况下不同结构的对比结果

原始AirNet默认使用50次迭代，因此,本文首先在50次迭代以及每次迭代2个隐藏层连接情况下对三种不同迭代残差连接结构(迭代图、迭代内和迭代间)进行了对比，每种结构都在两种不同初始化方法下进行了训练。

不同残差结构取得的结果如表2所示，其中由H-U初始化的迭代图连接取得了最好的结果。迭代图连接在两种不同初始化方式下的结果相差不大。迭代内连接只在H-U初始化的情况下可以正常训练，G-Z的初始化方式会导致模型训练失败，具体表现为损失函数值不下降。迭代间结构在两种初始化情况下都可以训练成功，其结果略优于迭代内结构，弱于原始的迭代图连接。

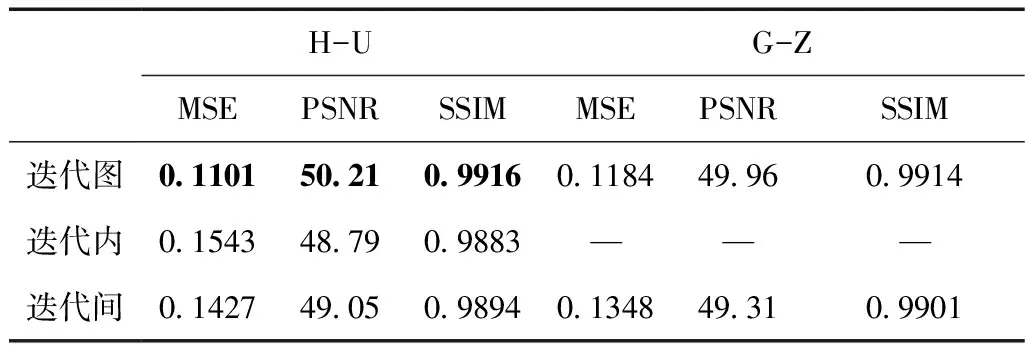
表2 50次迭代下不同迭代残差结构的定量结果

从上述对比可以看出，当总迭代次数较多而单次迭代中网络层数较少时，原始AirNet的迭代图连接效果最好;当迭代次数充分多时，两次相邻迭代间的图像更新较小，单通道的迭代图残差连接足以充分表达和传递特征信息。而迭代内和迭代间连接在此情况下对于提高前后层之间特征信息传递效率的作用有限，还失去了中间图像之间的连接，因此，重建性能受到轻微的影响。

在AirNet中，总迭代次数增加会扩大模型的尺寸，降低模型的计算效率。本文所提出的Efficient-AirNet模型的主要目标是通过降低模型所需的总迭代次数来提高模型的效率。因此，下文将降低迭代次数且提高单次迭代中的网络层数，对三种结构的重建结果进行评估。

3.2 10次迭代情况下不同结构的对比结果

表3所示为10次迭代、每次迭代间拥有10个隐藏层连接情况下三种迭代残差结构的结果。其中迭代图连接使用G-Z的初始化方法，而迭代内和迭代间连接使用了H-U的初始化方法。本文通过实验发现当迭代图连接使用H-U初始化时，以及迭代内和迭代间结构使用G-Z初始化时训练未收敛，因此表中省略了相关定量结果。

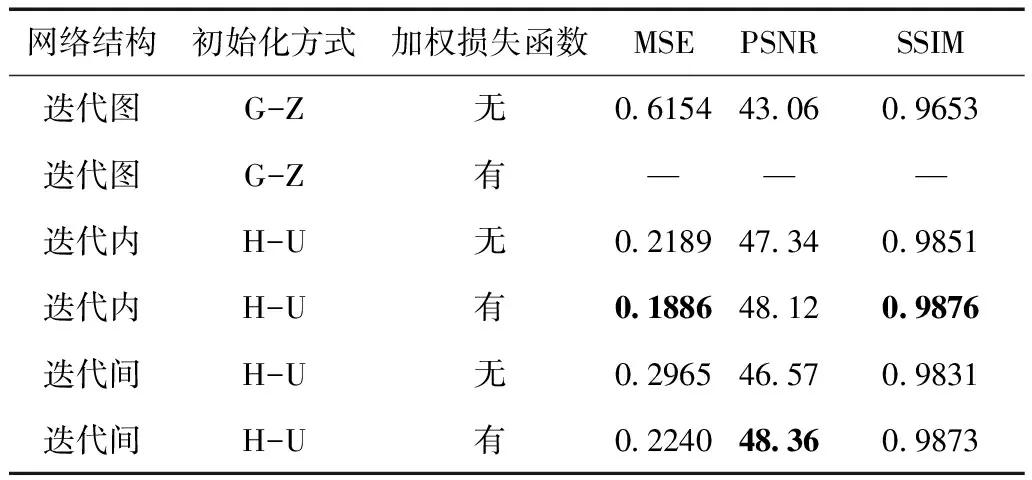
表3 10次迭代下不同迭代残差结构的定量结果

从表3中可以看出，迭代内和迭代间连接获得了比迭代图连接更好的重建指标。迭代内结构在使用加权损失的情况下取得了最佳结果。迭代间和迭代内连接在使用了加权损失函数之后，效果均有较大提升，最终两者定量指标比较接近。而迭代图连接在使用加权损失函数之后训练无法收敛。

从本文的实验结果中可以看出，当使用较少迭代并提高每次迭代中隐藏层数时，迭代内和迭代间连接结构在性能上优于迭代图连接。在隐藏层较多的情况下，这两种连接结构更有利于特征的传递，可以有效解决单次迭代中卷积神经网络层数较深时训练困难的问题。除此之外，卷积层初始化方式对于不同迭代残差结构的训练影响较大，在单次迭代内隐藏层较多的情况下，迭代图连接适合使用G-Z的初始化方法，而两种新结构适合使用H-U的初始化方法。

3.3 提高AirNet模型效率

降低迭代次数一方面可以减少投影反投影的次数，提高模型预测速度;另一方面可以减少训练期间需要存储的中间变量，减少模型的显存占用。上一节的实验结果表明新方法在10次迭代情况下也能获得较高质量的定量结果。本节将进一步对比10次迭代下迭代内和迭代间AirNet与50次迭代的迭代图AirNet的图像质量与效率, 对本文所提出的方法在提高AirNet效率方面的作用进行验证。

表4所示为三种迭代残差结构的图像质量指标和效率。为了验证增加单次迭代中卷积网络层数的作用，本节还增加了一项直接减少迭代图AirNet中迭代次数的实验。表中各模型后面的两个整数分别代表迭代次数和单次迭代中的隐藏层连接数。

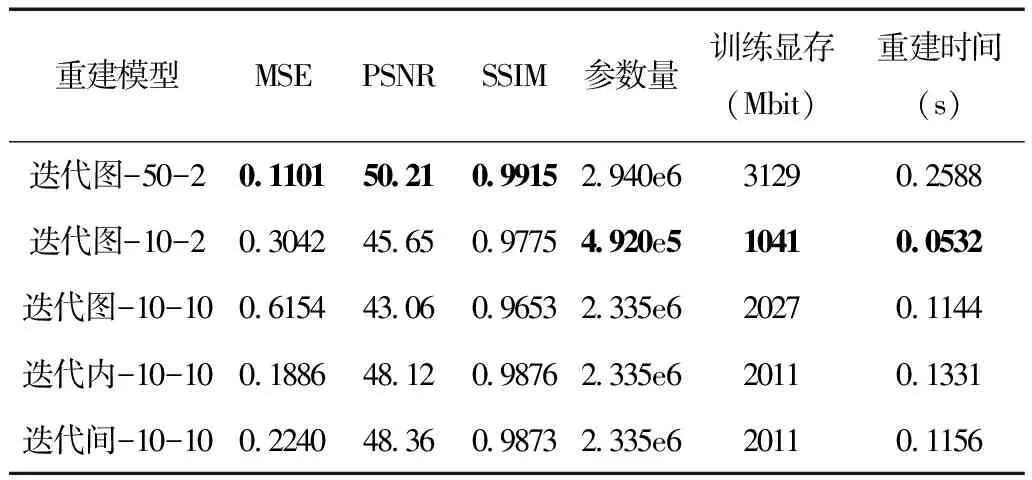
表4 不同迭代残差结构的图像质量指标和效率

从表4中可以看出，50次迭代的迭代图连接取得了最好的重建质量，但是其显存占用很高，计算时间也较长。当直接降低迭代图连接的迭代次数为10次，网络规模显著降低，显存占用减少了2/3，计算时间减少了约80%，但是PSNR和SSIM下降明显。在使用10次迭代并增加隐藏层层数之后，迭代图连接结果变得更差了。这是由于网络变深之后训练难度增加，虽然网络的表达能力提高，但最终模型性能反而会下降。而本文提出的两种迭代残差结构则可以解决此问题。可以看出最后的迭代内和迭代间结构相比于两种10次迭代下的迭代图连接的结果在PSNR和SSIM上都有较大提升。另外，两种新结构的显存占用相对于50次迭代的迭代图连接减少了约1/3，重建时间减少了约60%。

图3所示为表4中五个模型的重建图像。其中，Truth为标签图像，其余为基于AirNet的不同迭代残差结构的重建结果。Image、Inner与Outer分别为迭代图、迭代内与迭代间连接。通过对比可以看出，(b)中50次迭代的迭代图结果很好地恢复出了组织结构的细节，两个箭头所指示的区域与标签图像更加接近。当直接减少迭代次数为10次，得到的(c)中图像在箭头所指示的位置对比度降低，整体图像质量变差。(d)中10次迭代和10个隐藏层连接情况下的迭代图重建图像变得模糊，图像质量明显下降，箭头指示处的细节结构未能恢复。(e)与(f)中的两种新结构的重建图像与标签图像十分相似，很好地恢复了箭头所指示的细节，并且对比度和(b)中结果相近。

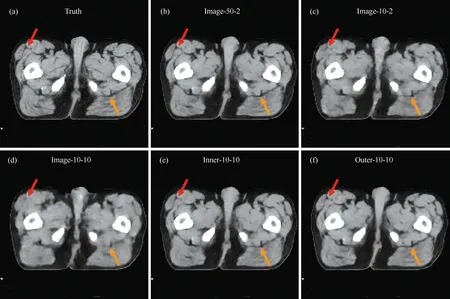
图3 三种迭代残差结构重建图像的对比，显示窗为[0.15, 0.2] cm-1

上述对比结果说明，两种新的迭代残差结构在保证和原始AirNet同等图像质量的同时可以有效降低AirNet所需迭代次数，进而减少训练中的显存占用和模型的重建时间，提高模型效率。

3.4 临床数据对比结果

各模型在临床数据上的重建结果如表5所示，迭代图连接仍然使用了50次迭代和2个隐藏层连接，迭代内和迭代间连接使用了10次迭代和10个隐藏层连接的组合。需要指出的是，本文通过实验发现使用加权损失函数在临床数据上并不能进一步提高两种新结构的性能，因此,本节的结果未使用加权损失函数。从MSE，PSNR以及SSIM等评价指标上可以看出深度重建模型的效果优于AIR-TV，而三种AirNet模型的结构显著优于FBPConvNet。

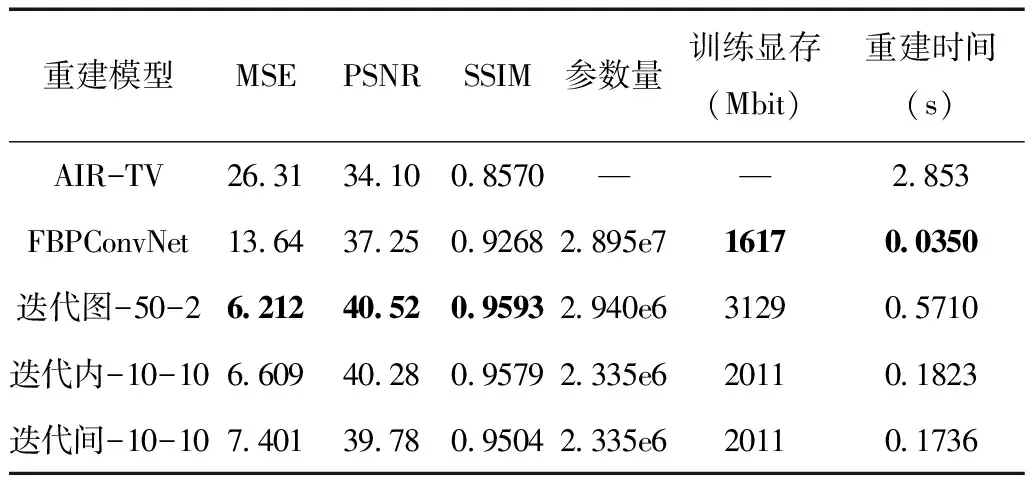
表5 不同方法在临床数据上重建结果的对比

三种AirNet模型之间的差距较小，迭代图连接结果最好，迭代内其次，迭代间最差。从表中还可以看出，迭代内与迭代间的网络参数量少于迭代图，所占用的训练显存减少了1/3，重建时间则不到迭代图残差结构的1/3。

图4所示为不同模型在临床数据上的重建图像，其中上面一行从左至右分别表示标签图像，AIR-TV和FBPConvNet的结果；下面一行分别是迭代图、迭代内和迭代间三种AirNet模型的结果，方法后面的两个数字分别表示迭代次数和每次迭代中的隐藏层连接数量。红框区域被放大用于对比细节重建效果。从图中可以看出，AIR-TV的重建结果出现过度平滑的现象，(c)～(f)则相对清晰。进一步观察后放大区域后可以看出，FBPConvNet未能恢复出标签图像中的组织细节。而三种AirNet模型则更为准确的重建出了相应的组织结构和边界。三种AirNet模型的重建图像之间差异很小，基本无法从肉眼上判断重建质量的优劣，这与表5得出的结论一致。

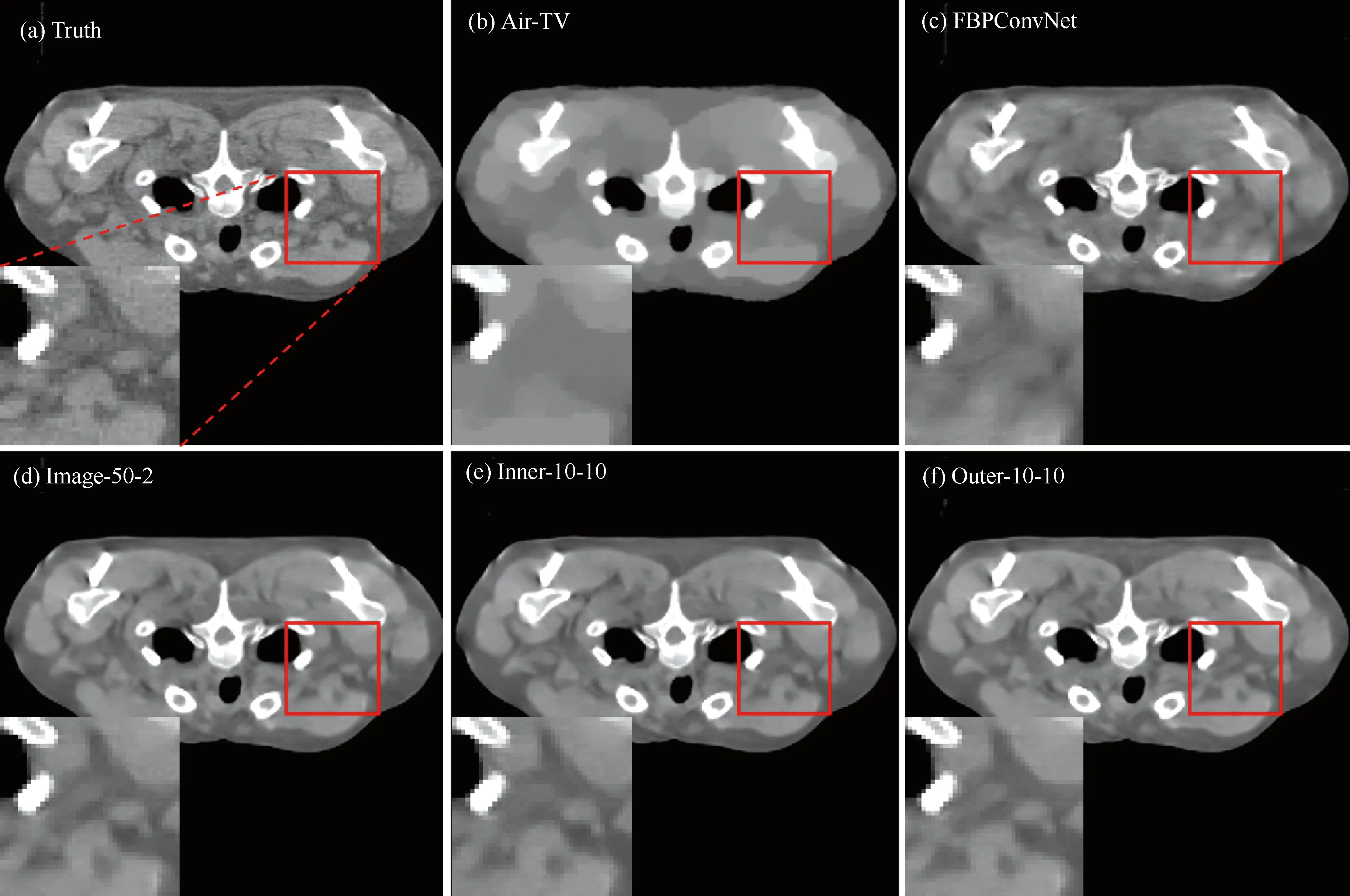
图4 不同重建模型在临床数据上的重建图像对比，显示窗为[0.3, 0.6] cm-1

4 结论

综合定量指标结果和视觉对比结果可以看出，原始AirNet在多迭代、浅网络情况下可以取得很好的图像质量，而本文提出的Efficient-AirNet在少迭代、深网络情况下图像质量更好。仿真结果显示，在保持同等水平重建质量的前提下，两种新迭代残差结构的Efficient-AirNet采用了10次迭代的结果与传统AirNet利用迭代图残差结构50次迭代的结果较为一致。因此，Efficient-AirNet成功降低了AirNet模型训练所需的计算资源，并提高了重建速度，将有助于推广AirNet模型至三维稀疏采样的CT数据重建应用中，提高其临床价值。