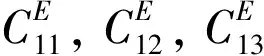基于PMUT的双层压电圆板自由振动分析

许 宽,张荣敏,张丽丽,周莎莎

齐鲁工业大学(山东省科学院) 机械与汽车工程学院,济南 250353

近年来,微型生物传感器发展迅速,随着超声技术的不断成熟以及MEMS(Micro-Electro-Mechanical-Systems)技术的进步,超声波微型生物传感器已深入到医疗、国防、电子与汽车等各行业部门[1]。在超声医疗成像以及超声检测领域中,超声微生化传感器已经广泛用于诊断各类癌症早期症状的工作中。在超声系统中,实现声电转换的装置即为超声换能器,是超声系统的重要部件之一,其性能参数将影响整个超声传感器的性能[2]。新型MEMS超声换能器(MEMS Ultrasonic Transducer)外形尺寸小,易于集成,且通常具有较高的灵敏度,使用范围广,引起大量学者的关注[3-4]。其中,相比其它微型换能器,压电微超声换能器(Piezoelectric Micromachined Ultrasonic Transducer,PMUT)具有极高的集成度,更易于实现各类换能器阵列的制造,成为微型超声传感器研究的热点[4]。

PMUT的核心构件是由压电材料制备的多层压电阵元。包含压电层,弹性支撑层,以及压电层上下表面的电极层。其力学特性决定了超声微型生物传感器的各项性能指标。基于PMUT结构的多层压电板的理论研究工作将为超声传感器的设计、制造提供理论支撑。

PMUT多层板结构中包含压电层,因此需要考虑压电材料特有的压电效应对PMUT的力学性能产生影响。对于微尺度下压电结构的力学性能,已有部分学者做了相关的研究,比如Mohammadimeh[5]根据修正的偶应力理论分析了纳米复合单层压电板的动力学特性。Kang[6]同样根据该理论分析了压电多层圆形微板的弯曲特性。Lou[7]分析了具有双层压电层的sandwich矩形层板的力学特性。最近,Korayem[8]基于该理论建立了多层压电矩形微板力学模型,并利用其模型分析了微板静态与动态力学特性。但是,这些基于高阶理论建立的力学模型较为复杂,为了降低模型与计算的复杂性,都是将模型简化为对称结构。宏观尺度下,Lee[9]在叠层板理论中考虑了压电效应的影响,建立了压电层合板理论。随后,有学者以该理论为基础,给出了矩形压电层合板的力电耦合模型。Heyliger[10]利用离散层模型研究了含有压电层的圆形层合板的自由振动。但宏观尺度下,学者们都将电场假设为沿板横向的常数。这一假设并不满足麦克斯韦静电方程。Lee等[11]将电势假设为沿厚度方向的正弦分布来满足麦克斯韦静电方程。

由此可见,现有宏观尺度与微尺度下的研究,大部分是将压电层板假设为对称结构。对于非对称层板的理论研究还不足。本文基于微型生化传感器中PMUT的结构特点,进行适当简化,忽略电极层厚度,同时考虑压电效应,基于Kirchhoff薄板理论提出了双层压电板的力电耦合模型。分析了压电效应对圆形双层板中性面位置、各阶频率与振型的影响,利用本文建立的模型可以有效减少PMUT设计过程中的实验成本与时间,为设计提供理论支撑。

1 双层压电圆板的力电耦合方程

基于PMUT实际结构,忽略电极层厚度,建立图1所示半径为a的双层压电圆板模型。其中压电层与弹性支撑层的厚度分别为h1,h2。考虑实际PMUT支撑层多为非压电材料,则双层圆板的中性面位置会偏离交界面,假设该模型的中性面与交界面的距离为d。

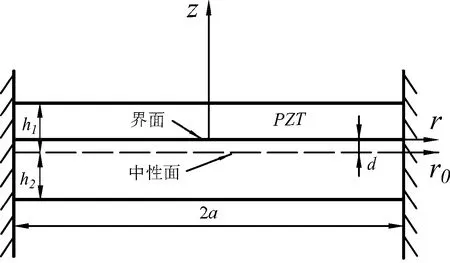
图1 包含压电层的双层圆板

如图1所示,假设r0-θ0平面位于压电双层圆板的中性面,则可以用以下公式描述其中性面位移场为:

(1)

(2)

其中,u,v分别表示r0与θ0方向的位移；w为压电圆板中性面沿z轴方向的挠度。根据以上中性面假设,可以写出压电层与支撑层接触面的位移场:

(3)

(4)

通过假设u0=-d∂w/∂r与v0=-d∂w/r∂θ,公式(3)和公式(4)可以表示为:

(5)

(6)

假设电场只沿z轴方向,因此压电材料的极化方向也是一致的。压电层两侧外加电场会使双层板产生相应的应变,根据应变位移关系,压电层与支撑层的应变可以表示为:

(7)

(8)

(9)

支撑层的应力分量可以表示为:

(10)

(11)

(12)

对于压电层,根据压电材料的本构关系可以推导出适用于压电薄板弯曲变形的本构关系(见附录A),因此压电层的应力分量可以表示为:

(13)

(14)

(15)

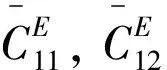
考虑PMUT在交变电场下工作时,分析压电层作为驱动元件，其压电效应对PMUT动力学性能的影响,假设电场只沿z轴方向分布。因此电场可以表示为:

Ez=Ecosθ,

(16)

其中,E与θ分别为交变电场的幅值与相位角。

当压电层板发生纯弯曲时,根据弹性理论,其横截面内应力为零,在上述假设电场下,r与θ方向的应力应该满足:

(17)

(18)

将公式(17)与公式(18)相减可得:

(19)

此时,对公式(19)进行积分,可得到中性面与接触面的偏移距离d:

(20)

公式(20)可以反应压电层对双层圆板中性面位置的影响,偏移距离d大小依赖于压电层与支撑层的材料和厚度。

利用基底层与压电层本构关系公式(10)-(15),可以得到双层压电圆板的合力矩:

(21)

(22)

(23)

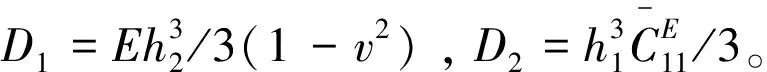
根据合力矩公式,双层板的剪切合力可以表示为:

(24)

(25)

把公式(24)和公式(25)以及定义的关系式u0=-d∂w/∂r,v0=-d∂w/r∂θ代入Kirchhoff板的控制方程:

(26)

可以整理出双层压电圆板的控制方程:

(27)

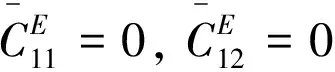
2 控制方程的求解

采用分离变量法,假设控制方程式(27)的解为:

w(r,θ,t)=W(r,θ)cosωt,

(28)

则代入公式(27),振型W(r,θ)将应满足:

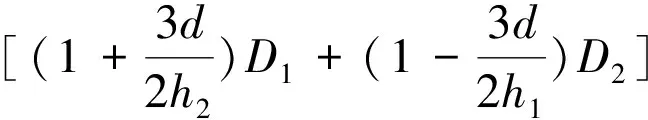
(29)

公式(29)还可以表示为:

(∇2W+α2W)(∇2W-α2W)=0,

(30)

其中,

(31)

进一步设振型:

W(r,θ)=R(r)Θ(θ),

(32)

其中,

R(r)=A1mIm(αmnr)+A2mKm(αmnr)+A3mJm(αmnr)+A4mYm(αmnr),

(33)

Θ(θ)=Amcosm(θ-φm)。

(34)

其中,m和n分别为节圆数与节径数,Am,φm和Aim为待定系数。Jm(αmnr),Ym(αmnr),Im(αmnr)以及Km(αmnr)分别为m阶第一、二类贝塞尔函数和第一、二类修正贝塞尔函数。对于中面完整的圆板,由于圆心处(r=0)第二类贝塞尔函数Ym(αmnr)与Km(αmnr)为无穷,所以在一般解中有A2m=A4m=0。根据公式(33)和公式(34)可以得到微分公式(27)的一般解。将一般解代入固支圆板的边界条件并使用贝塞尔函数的递归公式,即可得到特征方程:

(35)

解公式(35)可以得到频率系数αmna,再根据公式(31)中频率系数与固有频率的关系即可求得双层压电圆板的固有频率ωmn。

3 数值结果与讨论

为了分析压电效应对圆形双层板中性面位置、各阶频率与振型的影响,先选定双层板的材料。通常PMUT的压电层材料为PZT-4,弹性支撑层材料为硅。各层材料参数与尺寸值如表1所示。

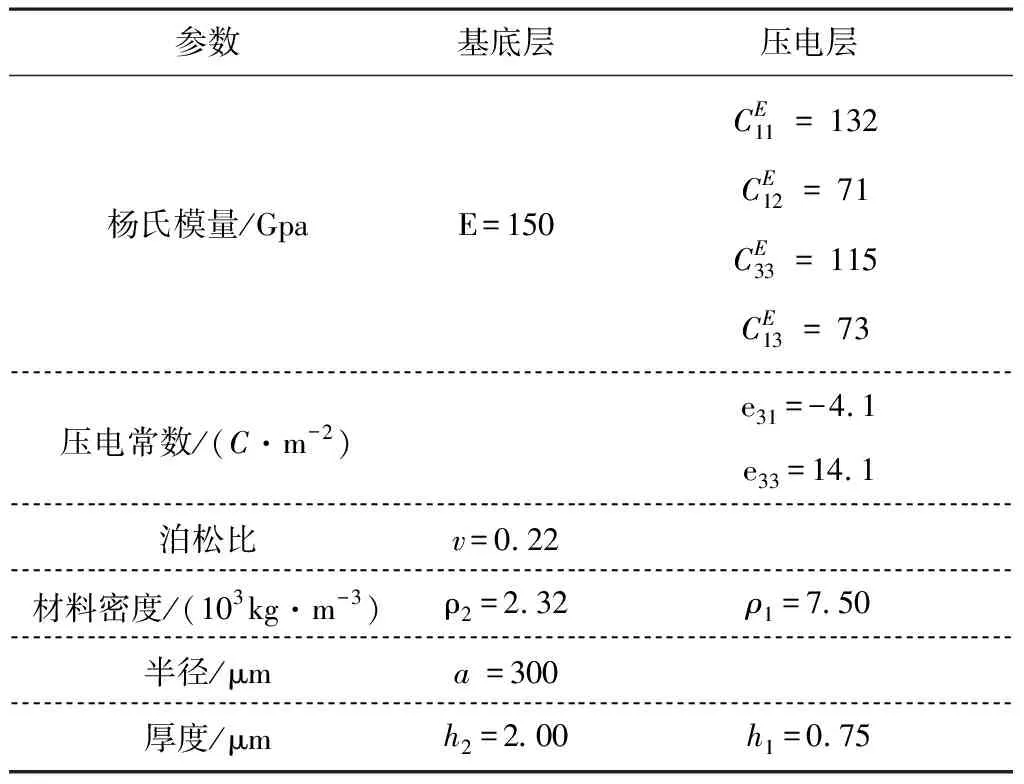
表1 包含压电层的双层圆板材料参数与尺寸参数[12-13]

3.1 压电效应对中性面位置的影响

考虑压电效应的影响,根据公式(20),压电层材料性质将影响双层圆板的中性面位置。为了具体分析压电效应对中性面位置的影响规律,基于本文建立的双层压电圆板模型,利用Matlab编程,得到中性面位置与PMUT板厚关系的曲线图,如图2所示。图2中的曲线具体描述了双层压电圆板中性面位置随PMUT厚度的变化规律。为了方便与已有普通双模量双层圆板的结果进行对比,参照文献[14]处理方式,假设各层厚度均为PMUT厚度的1/2。

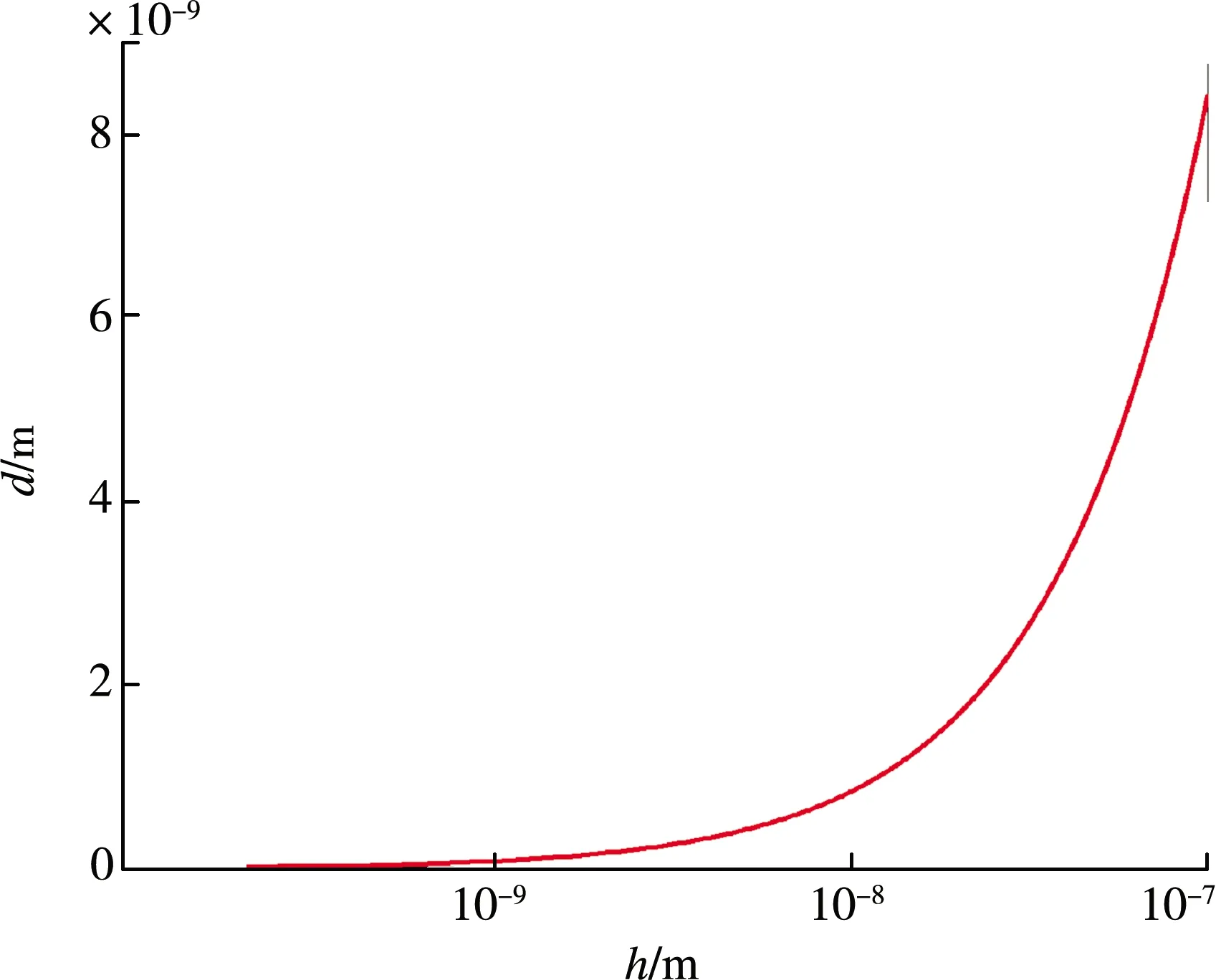
图2 压电效应对双层圆板中性面位置的影响

从图2可以看出,由于包含了压电效应的影响,非对称的双层圆板的中性面与两层接触面的距离d是随PMUT厚度h的增加而增大。并且当板厚较小时,压电材料产生的影响较小。随着PMUT厚度的增加,压电效应对中性面位置的改变变得更加显著。特别的,当板厚度大于1×10-8m时,压电材料对中性面位置的影响就不能忽略了。因此,当PMUT双层板厚度大于1×10-8m时,压电材料会使中性面的位置发生明显的改变,此时的压电效应的影响是必须要考虑的。进行PMUT尺寸设计时,当实际厚度不超过1×10-8m时,其性能指标可使用简单的单层板模型进行预测。当实际厚度超过1×10-8m时,其性能的预测需要考虑压电效应的影响,使用本文的模型可以更加确保预测结果的准确,从而节约实验时间与成本。

3.2 压电效应对固有频率与振型的影响

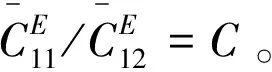
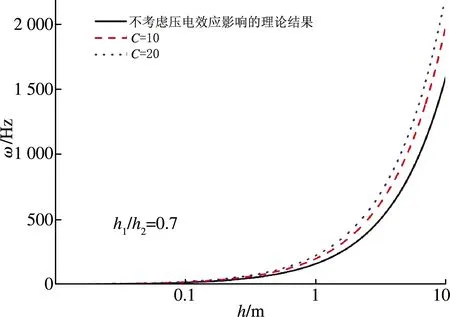
图3 压电效应对双层圆板固有频率的影响

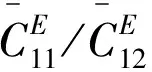
当双层压电板的厚度为定值,压电效应对各阶固有频率的影响在表2中列出。并与两层均为弹性支撑层材料的圆板的固有频率进行了对比。其中,保证两组对比模型的总厚度相等,均为h=2.75×10-6m；双层圆板的压电层与弹性支撑层厚度比如图3中取值h1/h2=0.7。

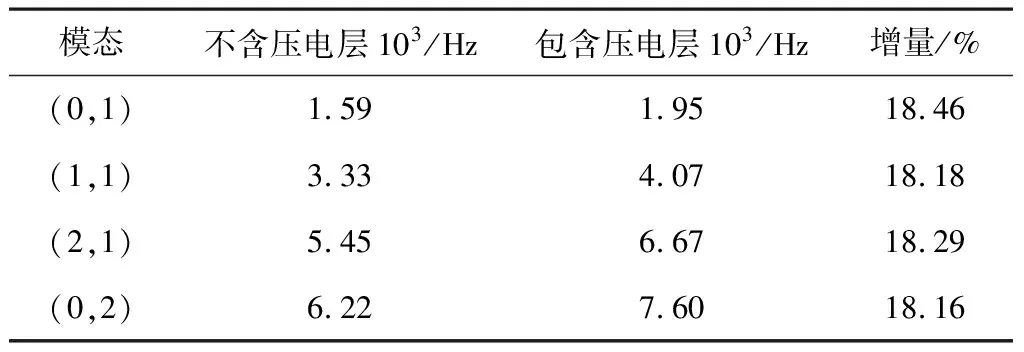
表2 现有模型与不考虑压电效应模型结果对比

从表2中可以发现,相比于只含弹性支撑层材料的双层板模型,现有模型的固有频率明显增加,压电效应对PMUT固有频率的影响是非常显著的。由表2的第四列数据可以看出,压电效应使PMUT双层圆板的固有频率大约增加了18%。同时,本文给出了考虑压电效应的双层圆板前四阶振型,如图4所示。

本文建立模型的有效性可通过与已有实验结果进行对比来验证。在对压电多层膜片振动模态的实验研究中,Olfatnia等[15]利用反射式数字全息显微镜捕获了圆形膜片各阶振型,如图5所示。通过与图4内的振型对比可以发现,利用本文建立的模型所得的结果与已有实验结果是一致的。其中,(0,1) 阶振型像一个单极子源,而更高阶模态则存在节径。节径的存在会影响PMUT振动时部分空气的运动,从而影响超声能量的传递,造成能量的衰减,因此,使用(0,1)阶模态更利于PMUT声能量的传递。

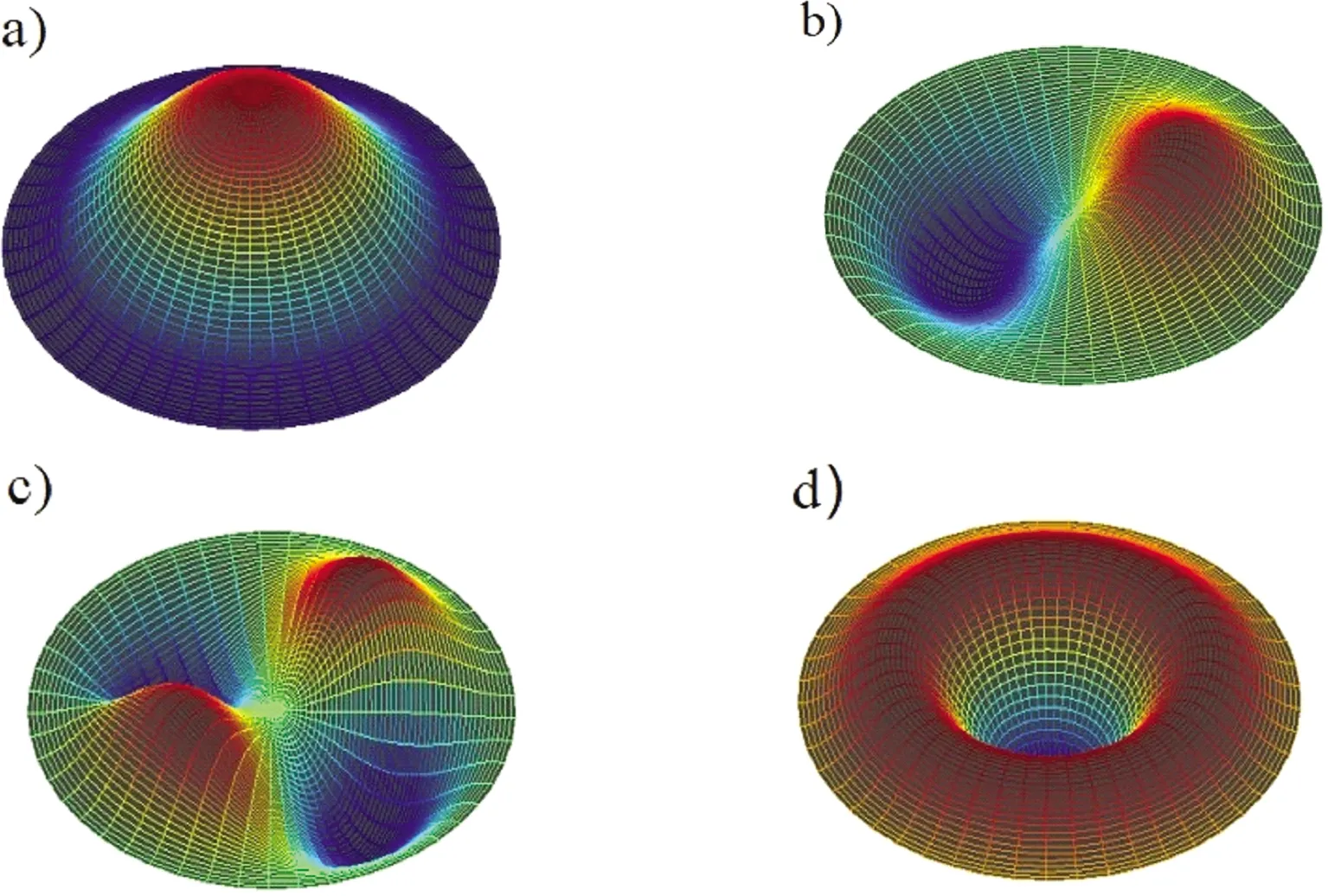
注:a)m=0,n=1；b)m=1,n=1；c)m=2,n=1；d) m=0,n=2。

4 结 论

考虑压电效应的影响,基于Kirchhoff薄板理论,建立了包含压电层的非对称双层圆板理论模型,并得到了固有频率的数值解。得到包含压电效应的双层圆板中性面位置表达式。基于压电材料的一般本构关系与双层板平衡关系推导了适用于压电材料弯曲变形的本构关系。通过与已有实验结果对比验证了本文模型的准确性。通过与普通双模量双层圆板对比,发现压电层的加入使中性面发生偏移,即压电材料对中性面的位置会产生影响,且对于厚度较大的板,其影响不能忽略。通过分析压电效应对双层板固有频率的影响,发现与普通材料板相比,压电材料对厚度较大的双层圆板的各项力学性能影响更显著。本文的理论模型与结果可为PMUT膜片的设计与制造提供理论支撑。

附录A

根据文中对电场的假设,压电材料一般本构关系可以表示为:

(A1)

基于Kirchhoff薄板理论,考虑r-θ平面内的弯曲变形问题,既有:

(A2)

其中:

(A3)

(A4)

(A5)