随机势场对氢原子能量本征问题的影响

刘星灿,哈斯花

(1内蒙古工业大学能源与动力工程学院新能源科学与工程系,内蒙古 呼和浩特 010051;2内蒙古工业大学理学院物理学系,内蒙古 呼和浩特 010051)

0 引言

众所周知,波函数可以完全描述某微观系统中一个微观粒子的量子态,而量子态的演化符合薛定谔方程给出的规律,即量子力学中的基本假定。对于与时间无关的势场中运动的粒子,可通过求解定态薛定谔方程得到体系的能量本征值及其对应的本征波函数,进而了解该系统中粒子的能量状态。但是大部分定态薛定谔方程无法精确求解,例如考虑外部干扰情形下的氢原子系统中电子的能量本征问题,数值解法的运用就显得十分重要。近年来,研究人员采用数值解法已求解了若干种外界影响下氢原子中电子的能级。其中,具有局部控制能力的B样条插值方法,通过调节其节点分布不但可以减少B样条基组数量,减少计算量,还可以设置重节点解决原子计算中遇到的奇点问题。作为一种强有力的数值解法,B样条插值方法一直是被广泛采用的[1-4]。

在一些微观系统中遇到外部随机干扰的情况很常见,因此外部随机干扰是讨论微观粒子的量子态时不可忽略的重要因素之一。为求解随机干扰下的能量本征问题,需要将随机扰动(如噪声干扰、热运动、外加随机电场等)看作外加势场,将定态薛定谔方程推广为一个包含随机势函数的微分方程,进而求得其随机干扰情形下的本征能量及其对应的本征波函数。部分文献中用随机扰动理论求解了氢原子的能级[5-7],取得了显著成果。Yang等[5]在对氢原子在外电场中的一级斯塔克效应的研究中,基于量子力学的微扰理论,得到了氢原子激发态的能级分裂情况。Zhang[6]在对氢原子核的热运动研究中,导入随机势,将本征方程转化为随机微分方程,得到了量子化实质上是一系列波函数分布的结论。Huang等[7]基于光子波粒二象性这一概念,在一维长程跳跃这一随机势模型中求解了相应的本征值和本征函数。

本文基于随机扰动理论,以氢原子为研究对象,用B样条函数研究其在等若干较低能级的能量本征值和本征波函数受扰动情况。并引入幅值不同的随机势,求解对应的本征波函数,进行比较和讨论。研究结果表明:当随机势强度范围在0～0.01u0(u0=27.2114 eV,为原子单位)时,电子分布几率与中心力场下的电子分布几率相似;当随机势场的强度范围逐渐加大至0.1u0时,电子分布几率变化更为频繁;随机势范围继续增大到5u0时,中心力场作用完全弱化。且电子分布和几率还与主量子数n与角量子数l密切相关,量子数越高的体系越不稳定。

1 随机势场影响下氢原子的能量本征方程

2 B样条函数的定义与性质

2.1 B样条基函数

B样条函数是贝塞尔曲线的一般化,最早于1946年由Schoenberg创造[8]。B样条基函数的递归公式定义为[9]

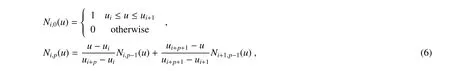
其通称为Cox-de Boor递归公式,其中Ni,p(u)代表第i个p次B样条基函数,基函数的次数为p,ui为节点,也就是分隔点。

2.2 样条函数基函数的导数

B样条基函数具有可微性[10]

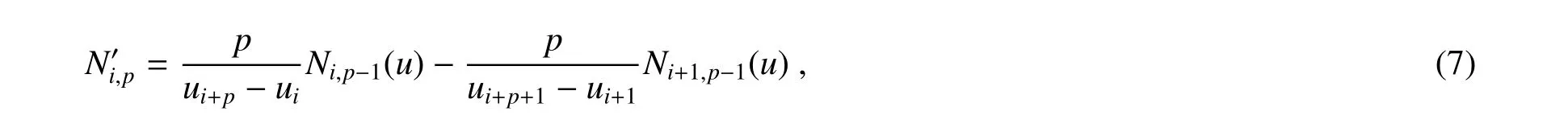
其基函数及其导数的函数关系如图1所示。

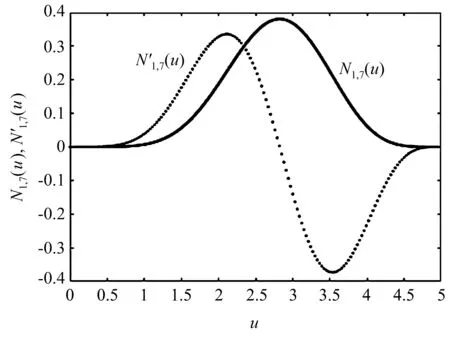
图1 七阶B样条的基函数及其导数Fig.1 Basis function and derivative of the seventh order B-spline function

3 B样条函数求解氢原子定态本征方程

将氢原子中电子的径向波函数用B样条函数展开得

式中:Pi是控制点,是第i个k阶B样条函数的展开系数;k为B样条函数的数目。将(8)式代入(4)式可将定态薛定谔方程化为HP=ESP的形式。对全空间积分可得重叠矩阵的矩阵元为

哈密顿矩阵的矩阵元为

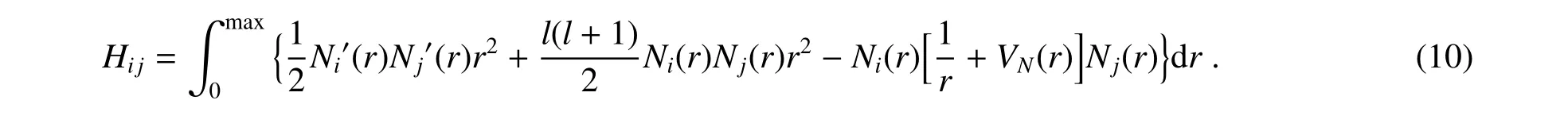
由此,便将含随机势的微分方程推广为广义本征值问题。通过使用lapack库中的dsbgv算法对上述矩阵进行对角化处理,可以得到氢原子中电子的能量本征值矩阵E。

对于上述矩阵元的数值积分,采用梯形法则求解。通过对积分区间的分割,分别计算每个分割区间的梯形面积,将其求和,最后得出区间内积分的近似值。

4 结果与讨论

首先讨论不考虑随机扰动时的计算结果,求出氢原子中电子仅在中心力场作用下的本征能级及其本征波函数,寻找B样条函数求解氢原子能量的规律,并以此验证该方法的可行性;其次讨论氢原子中的电子在随机势场与中心力场共同作用下的计算结果。重点关注本征波函数趋势的变化,分析其变化规律,并将其与仅在中心力场作用下的结果进行对比。

4.1 仅在中心力场作用下的计算结果与讨论

氢原子中的电子仅在中心力场作用下,各能级在不同积分上限下对应的B样条函数计算结果如表1所示(R代表积分上限,表中能量单位均为u0)。

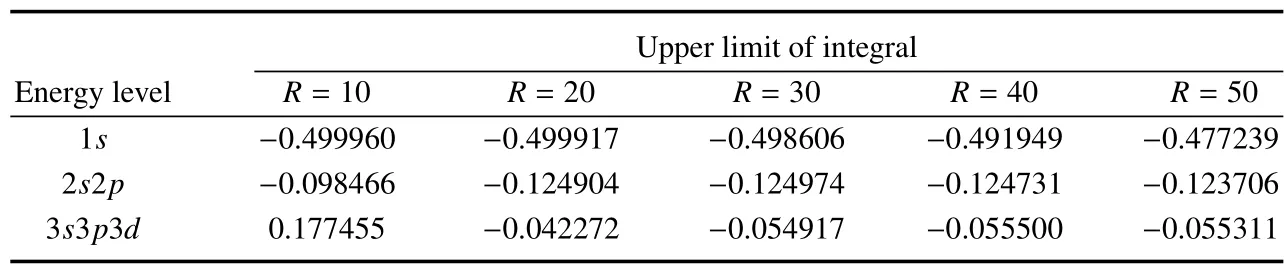
表1 氢原子中电子本征能级的计算结果Table 1 Calculation results of electron intrinsic energy levels in hydrogen atom

由计算过程可知,B样条函数的节点分布会大大影响基函数的拟合效果。并且本征波函数在趋近于第一个奇点即r→0时分布较为密集,而当r→∞波函数则逐渐趋近于0。考虑到上述因素,采用指数型节点分布能更好地拟合其波函数。考虑到本征方程在r=0、r=∞存在奇点,故在积分下限和积分上限附近加入重节点,以此加大拟合的波函数在奇点附近的本征波函数为0的权重,从而解决奇点问题。

表1的求解结果采用6阶B样条函数,以0.01作为梯形积分的步长,30个指数型节点、8个重节点的节点分布,按照积分上限R对氢原子中电子的三个低能级进行求解。从结果中可以看出,当积分区间比较小时,由于节点在靠近0的地方较为密集,且第一能级的波函数主要在靠近0处分布,所以第一能级的计算结果较为准确。当节点区间不断扩大,节点在区间内变得相对均匀,第一能级计算结果精度下降,但是第二、三能级的计算精度上升。所以,在编程计算过程中需注意,节点分布对能级的求解是非常重要的因素。

在求解出精确的本征能级后,将能量E代入(5)式求解常微分方程[此时VN(r)取为0],即可解得未受随机势干扰情形下本征能量对应的本征波函数。图2为不同角量子数对应的电子的径向分布概率(波函数采用R=40的计算结果绘制,其中长度以r0=0.529×10-10m为单位)。从图中可以看出,本征能级计算准确,本征波函数拟合情况良好。

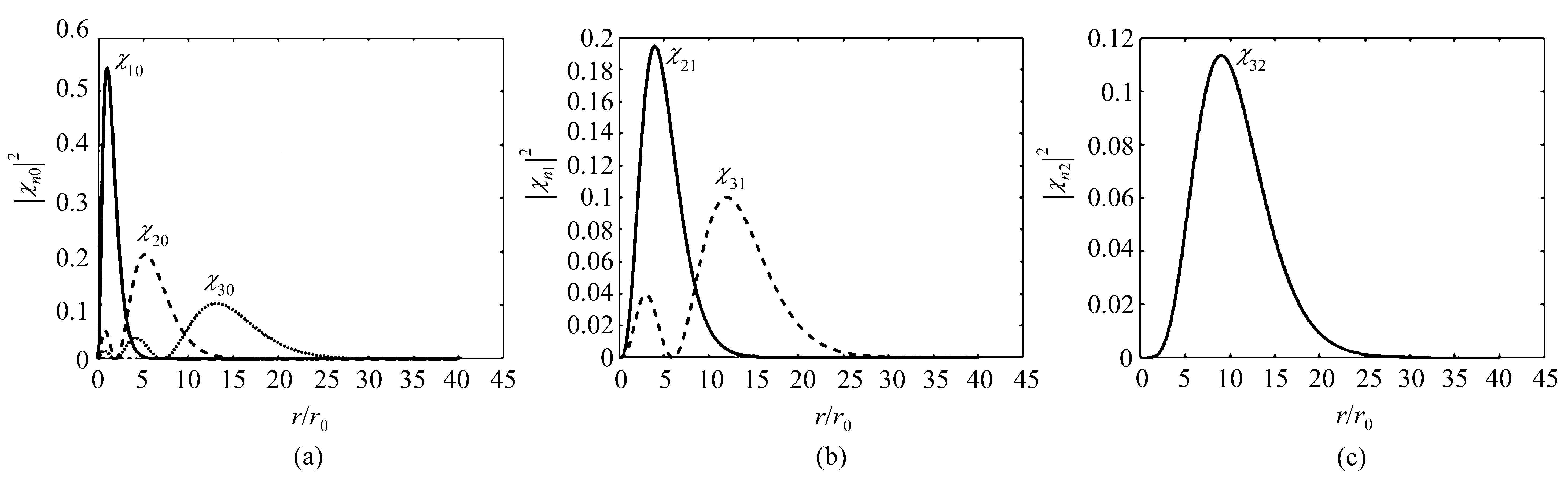
图2 角量子数l=0,1,2时电子的径向分布概率Fig.2 Radial distribution probability of electrons with angular quantum numbers l=0,1,2

4.2 考虑随机势场作用下的计算结果与讨论

加入随机势VN(r)后,电子本征波函数受到不同程度的干扰。由于每次生成的随机势场强弱不同对于电子本征态的影响显著不同,经过大量实验后,在n=1与n=2能级中选出四种不同强弱的随机势进行绘图并讨论,其中随机势的分布采用条形图进行绘制。

4.2.1 n=1,l=0时波函数在随机势场下的情况

图3为施加不同大小的随机势能对系统电子径向分布概率的影响。由图可见,当主量子数n=1、角量子数l=0时,系统的本征波函数在随机势场的影响下较为稳定,相较于其余高能级本征波函数,该本征态是最稳定的。当随机势范围取为0～0.1u0,系统依然主要受到中心力场的作用。当随机势场范围增加到0～1u0,电子的分布几率便开始发生较为明显的波动,随机势场的干扰出现了可观察到的影响。随机势场范围增加到0～5u0时,电子分布几率出现更多波峰,波函数变化趋势更加多样化。但是接近中心的区间内产生了较大的变化,远离中心的区域受到随机势场的影响较小,电子的几率依然主要分布在靠近中心的区域,说明中心力场的影响还未完全消失,此时体系受到中心力场与随机势场的共同影响。

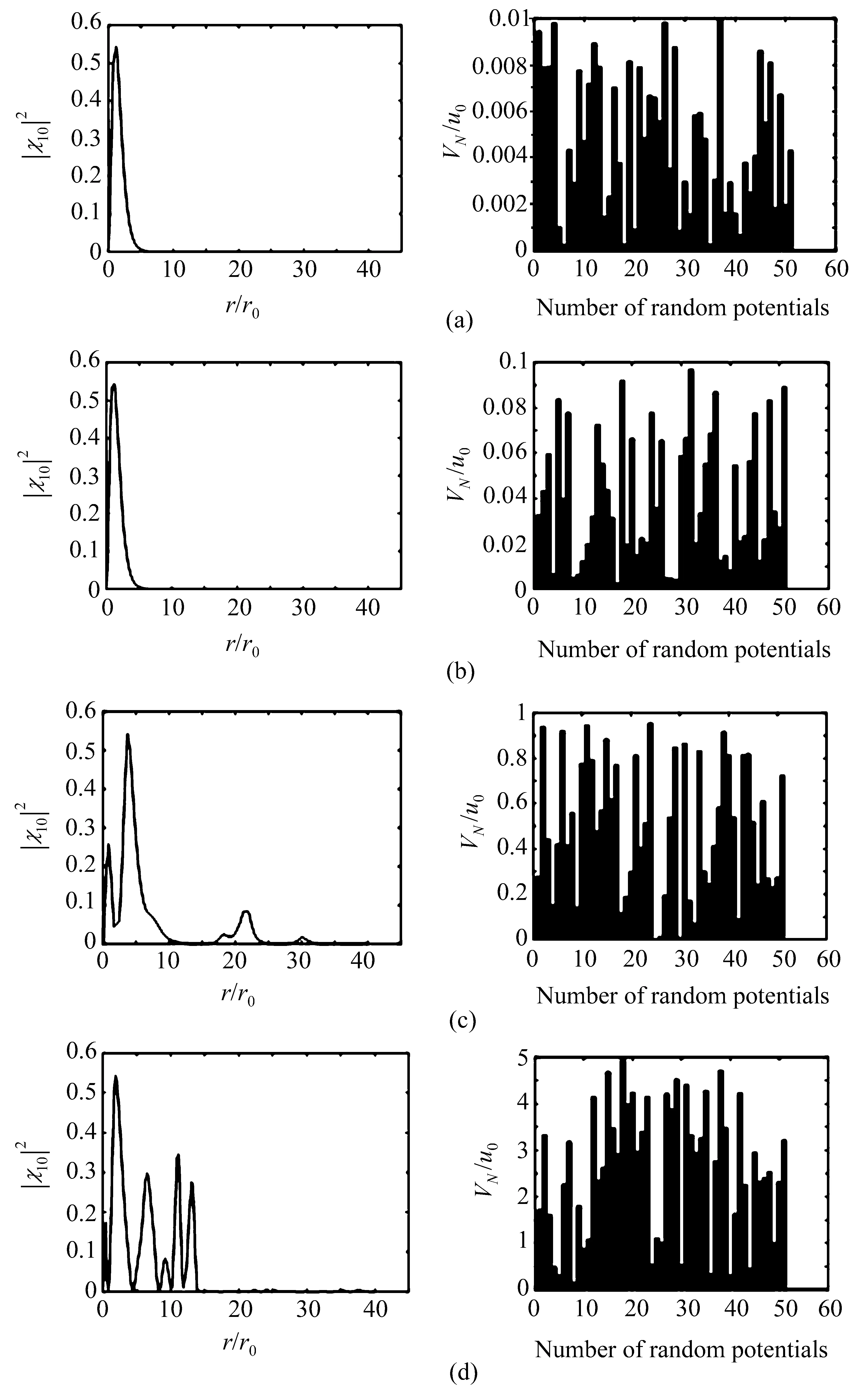
图3 施加不同大小的随机势能对n=1,l=0时系统电子径向分布概率的影响。随机势能范围分别为(a)0～0.01u0,(b)0～0.1u0,(c)0～1u0,(d)0～5u0Fig.3 Effect of different sizes of random potential energy on the radial distribution probability of electrons in the system during n=1,l=0.Random potential range are(a)0～0.01u0,(b)0～0.1u0,(c)0～1u0,(d)0～5u0,respectively

4.2.2 n=2,l=0时波函数在随机势场下的情况

由图4施加不同大小的随机势能对n=2、l=0时系统电子径向分布概率的影响可知,与χ10态不同,当随机势范围增加到0.1u0时,对波函数的干扰已经出现可观测的变化,如图4(d)所示,波函数在r=20处甚至出现了一个波峰。但总体而言,考虑随机势的波函数整体图形与只有中心力场的情况相当,说明此时中心力场影响较强于随机势影响,电子的分布几率受中心力场影响更大。当随机势继续增大时,波函数的变化更为显著。对比χ10态的情况,电子的分布几率更加杂乱无章,说明随着主量子数的增加体系受到随机势场的影响将更加显著。

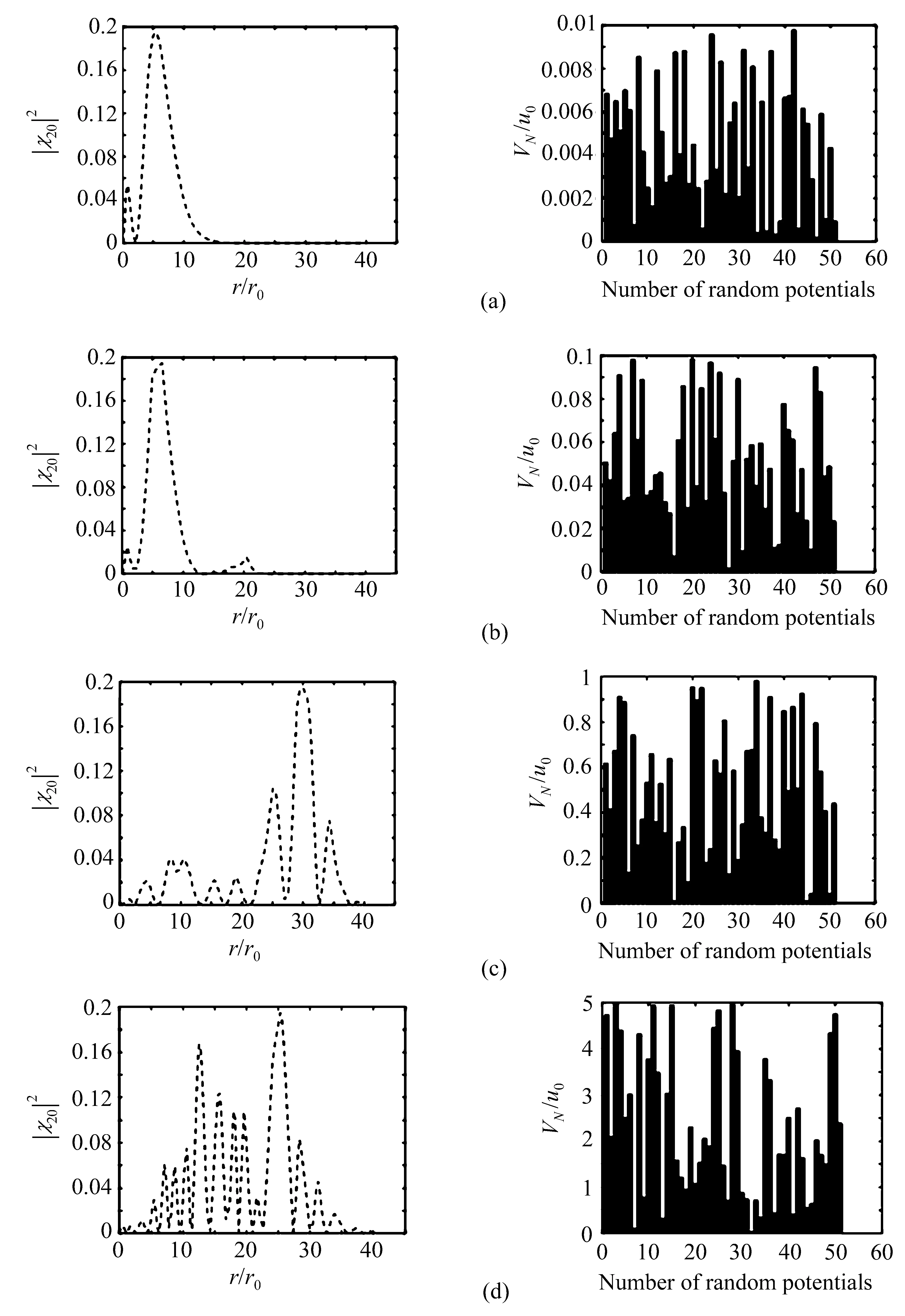
图4 施加不同大小的随机势能对n=2,l=0时系统电子径向分布概率的影响。随机势能范围分别为(a)0～0.01u0,(b)0～0.1u0,(c)0～1u0,(d)0～5u0Fig.4 Effect of different sizes of random potential energy on the radial distribution probability of electrons in the system during n=2,l=0.Random potential range are(a)0～0.01u0,(b)0～0.1u0,(c)0～1u0,(d)0～5u0,respectively

4.2.3n=3能级对应的各波函数在0～0.1u0随机势场下的情况

由图5观察同一随机势场中对应不同能级的情况可知,随机势强度范围增加到0.1u0时,l=0、l=1及l=2的图形总体规律均不变,但会出现某些区域受到干扰而产生额外波峰的情况。当波函数范围继续增加时,波函数将在整个积分区间都展示出杂乱无章的状态,与χ10及χ20主要分布在靠近中心的区间内的情况呈现鲜明对比。

另外,由图5(c)可以看出,χ32的情况与以上几种相比,其主量子数和角量子数都是最多的,分布几率最不稳定,最易被随机势场影响。

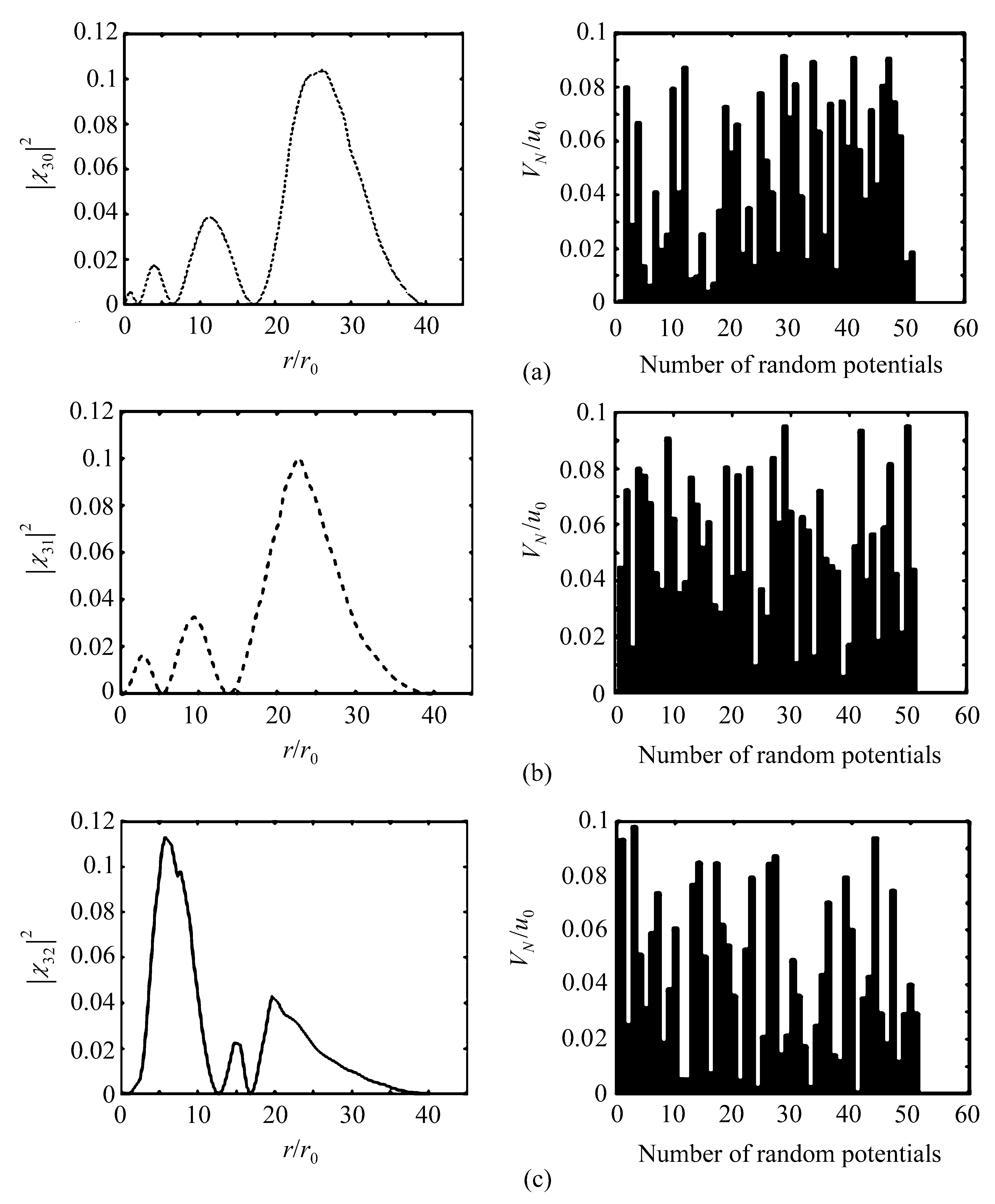
图5 同一随机势场中对应不同能级的情况。(a)l=0;(b)l=1;(c)l=2Fig.5 Different energy levels in the same random potential field.(a)l=0;(b)l=1;(c)l=2

5 结论

通过B样条函数详细计算了氢原子n=1,2,3时的能级,并给出对应的本征波函数。进而考虑随机势场的影响,对外加势场下的氢原子波函数图形进行了对比分析。得出的总体结论为:当随机势强度范围在0～0.01u0时,随机势场的影响几乎可以忽略不记,电子分布几率与中心力场下的电子分布几率相似。当随机势场的强度范围逐渐加大至0.1u0时,将对波函数的图形结果产生较显著的影响,且电子分布几率变化更为频繁。随机势范围继续增大到5u0时,中心力场作用完全弱化,电子的分布几率几乎完全由随机势场决定。此外,当确定随机势的范围不变,随着主量子数n与角量子数l不断增大,电子几率分布受随机势影响越大,电子分布随机性越强。可见,较高量子数的体系更加不稳定,其中心力场的作用更容易被外加势场破坏。