基于最小二乘的频谱分析仪频响温漂补偿方法

张吉伟 时杰飞 詹永卫 张超

【摘要】    本文针对温度变化影响频谱分析仪中的多级放大、滤波等模块的频响，从而导致其幅度测量精度下降的问题，提出了一种基于最小二乘法的分段线性拟合频响补偿权值曲线的方法;并根据频谱分析仪的实际工作温度变化曲线模型，提出了一种与开机时间相关的温度线性空间的分段划分方法;同时给出了此方法在频谱分析仪中的应用补偿流程。通过仿真分析，该方法有效的使频响补偿值跟踪温度的变化，提高了幅度测量精度，解决了分析仪在开机预热阶段的幅度偏差大以及测量连续性问题。

【关键词】    最小二乘法    分段拟合    温度    频响补偿

A method of compensation about spectrum analyzers frequency response effected by temperature drift based on least squares

Zhang Jiwei   Shi Jiefei   Zhan Yongwei   Zhang Chao

（The 41st  Research  Insitute of  CETC，  Qingdao  266555，China ）

Abstract： This paper proposes a method of piecewise linear fitting of the frequency response compensation weight curve of a spectrum analyzer based on the least squares， which focuses on the influence of temperature changes on the frequency response of multi-stage amplification and filtering modules in spectrum analyzer. A segmentation method of temperature linear space related to start-up time is proposed according to the actual working temperature curve model of the spectrum analyzer. At the same time， the application compensation process of this method is given. Through simulation analysis， this method effectively makes the frequency response compensation value track the change of temperature， improves the accuracy of amplitude measurement， and solves the problem of large amplitude deviation in the preheating phase of the analyzer and the continuity of high-precision amplitude measurement.

Key words： least squares method    Linear fitting method    temperature    frequency response

引言：

在频谱分析仪中，幅度精度是一个非常重要的技术指标，其在仪器测试中体现在信号的频率响（简称频响）应测量误差上[1]，目前国外的频谱仪，像是德科技的N9040B系列频谱分析仪到50GHz频段的频率响应在20到30℃的温度范围内误差在±3.2dB以内;R&S公司的FSVA3000信号和频谱分析仪44GHz频段的频响在20到30℃条件下误差在±1.97dB以内，在0到50℃条件下误差在±4dB以内。信号经过各级通路在不同的温度环境下其频率响应误差不同，即产生温度漂移（简称温漂）[2-3]。

最小二乘法广泛应用于系统优化、最优化求解等领域的成熟的统计数据分析方法[4-6]。利用最小二乘法訓练学习温漂的补偿权值，拟合补偿权值曲线，使得频谱分析仪获得高的幅度测量精度。

一、信号和频谱分析仪频响补偿

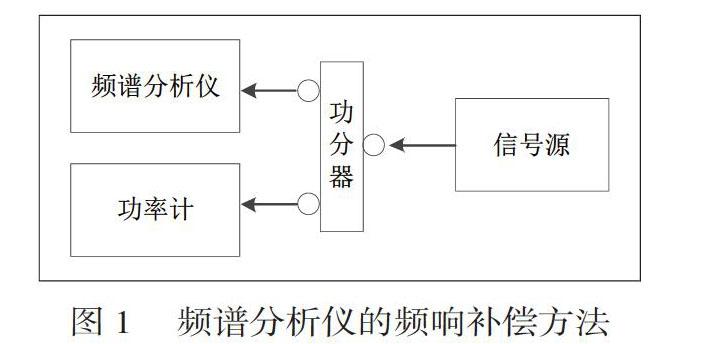
频谱分析仪频率响应补偿方法如图1所示，信号源产生不同频率的信号，经过功分器功分两路分别给频谱分析仪和功率计，通过计算测量功率计与频谱分析仪的差值即为当前频率下的补偿值。

在大多数的频谱分析仪中，仅仅对频响补偿一次，在所有的测试条件下用这一次的补偿值。频谱分析仪在刚开机阶段，其内部温度变化较大，频率响应也变化较大。为了解决开机的温度变化影响，目前常用的补偿方法是待频谱分析仪开机预热一段时间，使其工作在温度相对稳定的条件下再进行频响补偿，如图2所示。但是，频谱仪内部模块较多、电路复杂，所需要的预热时间较长，通常需要20分钟以上，且在补偿之后，每次开机预热期间频响误差大，是不进行幅度测试的;另外频谱分析仪的工作环境复杂多样，在其补偿时差别较大时，其幅度测量误差也会增大。因此，采用开机预热稳定后测试存在很多弊端的。

为了克服因温度环境变化较大带来大的幅度测量误差，一种方法是在频谱仪内部设计标准的校准源信号。由于频谱仪的频段很宽，校准信号数量有限，仅在校准的频点幅度准确度高，并且内部校准源也会受温度的影响，同时也增加了成本。另外定时校准时需要停止测量，对用户使用体验不佳，在连续测试的需求下这种校准模式也是不可用的。

二、基于最小二乘的温度补偿方法

2.1 最小二乘法的温度补偿模型

受温漂的影响，单次补偿以及引入校准信号，无法实现连续测试条件下的高精度幅度测量。因此，获取宽频带频谱分析仪的频响温度特性，并自动进行实时补偿，有效的解决温漂导致大的幅度测量误差。利用最小二乘法将权系数曲线分段拟合，在每一段内近似成线性，可获得高精度拟合曲线。

在每个受温度影响的模拟前端模块电路上引入温度传感器，实时监测各个模块的温度，假设有M个模块受温度的影响会影响到频响参数，如图3所示

在每个分段内近频响变化与温度似成线性，关于拟合权系数a。可获得方程组如下式所示：

系数矩阵T为：

系数矩阵T，以及补偿值p为频响补偿时的训练数据。在进行数据补偿过程中，获取多组训练数据，即进行多次频响补偿，使得N>M。

在最小二乘意义下，使得误差的模的平方和

取得最小值，方程的唯一解为：

2.2 温度区间的分段划分

由于整机和模块的散热设计，每此个模块升温后的工作温度是相对稳定的。由于信号和频谱分析仪从环境温度到已预热阶段，温度传感器1的升温变化区间[T11，TN1]到温度传感器M的升温变化区间[TM1，TNM]的升温趋势相似，如图4所示，所以温度线性空间的分段划分可以近似在时间段上划分[8-10]。

虽然同一台频谱仪内部的不同传感器的温度变化趋势相似，但是不同的环境温度[T11，TN1]与[TM1，TNM]的划分区间的对应关系不同。

为了解决不同环境起始温度带来的分段差异性，使的分段划分更合理，对信号分析仪进行温度变化曲线统计学习，将温度补偿系数分为多组，使其更加逼近线性。同时学习到稳定阶段的时间，对稳定阶段学习训练尽量多的数据，从而提高稳定阶段的精度。

2.3 温漂补偿流程

基于最小二乘法的信号和频谱分析仪频率响应温漂补偿方法分为三个阶段：

1.温度曲线学习阶段，频谱仪放在环境试验箱里，设置不同的环境温度，学习不同的环境温度下的各模块温度传感器的变化曲线，并划分不同的线性段;

2.训练补偿阶段，频谱仪在环境试验箱里，在不同的环境温度下观测温度值与频响补偿值，根据阶段1将补偿数据分组，利用最小二乘法拟合温度与频响曲线;

3.用户使用测量阶段，实时获取各模块的温度值，并匹配所处于的线性段，得到当前状态下的频响补偿值。

三、建模仿真分析

根据对频谱仪的频响温漂特性以及温度试验箱的实测数据，频谱仪一般的工作环境温度为0℃到50℃范围内，同一环境温度不同的预热时间段信号的频响差异达±6dB，不同的环境温度同一信号的频响差异达±4dB。据此进行建模仿真。

假设在信号分析仪中有三个模块的频响受温度影响。在环境温度为18℃的环境下的温度变化曲线如图5所示。将曲线划分为4个线性拟合区间，其中分段1、2、3为预热阶段，分段4為稳定阶段，即在此环境温度下18min之后，频谱分析仪的温度拟合系数到稳定阶段。

对环境温度为18℃和34℃的条件下的温度与频响进行拟合并与仿真补偿值对比。如图6所示，常用的单次补偿方法受温度影响误差很大，在预热阶段更明显;基于最小二乘法的频响温漂拟合方法可以有效的使补偿值跟踪温度变化，且误差降到很小。

四、结束语

针对频谱分析仪的频响受环境温度以及工作状态温度的影响大，提出了引入温度传感器，通过最小二乘法分段线性拟合的方法学习训练频响补偿值，并根据针对频谱分析仪的温度变化特性，提出了温度分段划分方法，降低了在多元分段线性拟合的线性区间的排列组合的多样性，通过仿真分析，该算法可以有效的使频响补偿值跟踪温度的变化，且误差也小，解决了频谱分析仪在预热阶段的测试问题，且该算法不用间歇校准，保证了频谱仪使用的连续性。

参  考  文  献

[1] 李凡，庄涛，徐宏光. 频谱分析仪测量电平的不确定度分析与评定 [J]. 品牌与标准化. 2016 （03）

[2] 李剑雄.频谱分析仪与测量技术基础 [M]. 北京人民邮电出版社. 2011：13-16.

[3] 卞剑. 频谱分析仪自动校准中的问题及解决方式 [J]. 计测技术. 2016 （01）

[4] 孟红波. 一种基于最小二乘法和RBF神经网络的多步误差补偿方法  [J]. 测试技术学报. 2015 （06）

[5] 于湘涛. 基于小波最小二乘支持向量机的加速度计温度建模和补偿  [J]. 中国惯性技术学报. 2011 （01）

[6] 杨宾峰. 基于最小二乘的地磁场测量误差补偿技术 [J]. 空军工程大学学报. 2017 （06）

[9] 郭星星. 基于循环神经网络的多核芯片热管理技术研究 [D]. 电子科技大学. 2019