径向热管管内液池沸腾换热模型的探讨

刘苗苗，马永康，麻泽松，李志桐，李 鹏，邹琳江

（安徽工业大学 能源与环境学院，安徽 马鞍山 243002）

热管是一种优质、高效的传热设备，在工业生产、余热回收领域有着重要的作用。同轴径向热管由外管、内管以及管内工质构成。在稳态的条件下，径向热管基本传热过程是外管外壁吸收热量传递给管内液态工质，液态工质发生相变汽化产生蒸汽，蒸汽在内管外表面凝结而将热量传给内管内的流体，从而达到换热效果[1-3]。关于径向热管的传热模型，文献[4-5]均建立一套完整的传热模型，径向热管的外管管外传热和内管管内传热模型已有大量的实验可验证模型准确性，但关于管内液池的模型，由于在封闭有限空间内研究较少。文献[4-5]将管内液池的沸腾类比大空间池状核态沸腾，并以此建模分析。但上述关于管内液池的沸腾模型在计算实际径向热管的外管壁温度存在较大偏差，管内液池沸腾换热模型是造成偏差的主要影响因素。本文对液池换热采用膜态沸腾[6]及核态沸腾分别进行建模计算，并与实验数据比较，拟合出适合径向热管管内液池沸腾蒸发换热模型。

1 模型分析

1.1 物理模型

径向热管的传热过程如图1所示。过程1为外围高温流体与热管外管壁对流换热；过程2为热量通过外管壁导热传热给管内空间，外管内壁面换热由两部分组成：管内蒸汽与内壁面对流换热（过程3）和液池蒸发沸腾换热（过程4）；过程5为管内蒸汽在内管外壁面凝结换热；过程6为内管壁导热将热量传递到内管；过程7为内管管内冷却水与内管内壁面对流换热，通过冷却水将热量带走。

图1 径向热管传热模型简图

对整个径向热管的工作过程进行热分析，忽略热管的污垢热阻等次要因素影响，建立的热阻分析模型如图2所示。将每个热量传递过程简化，热阻R1为高温流体与外管壁对流换热热阻；R2为外管壁的导热热阻；R3为蒸汽与外管内管壁对流换热热阻；R4为沸腾蒸发热阻；过程3与过程4都是与外观内壁换热，饱和蒸汽温度Tv与池内饱和水温Ts相同，故认为R3和R4并联，并联热阻；蒸发段总热阻Re=R1+R2+Rb；R5为蒸汽凝结热阻；R6为内管导热热阻；R7为冷却水与内管壁对流换热热阻；Tf为烟气温度；Tw1为外管壁温度；Tw2为外管内壁面温度；Tw3为内管外壁面温度；Tw4为内管内壁面温度；Tout为冷却水出口温度；Tin为冷却水进口温度；冷却水平均温度Tl=0.5×（Tin+Tout）。

图2 径向热管热阻分析图

1.2 数学模型

径向热管的传热计算遵循下述的数学描述：

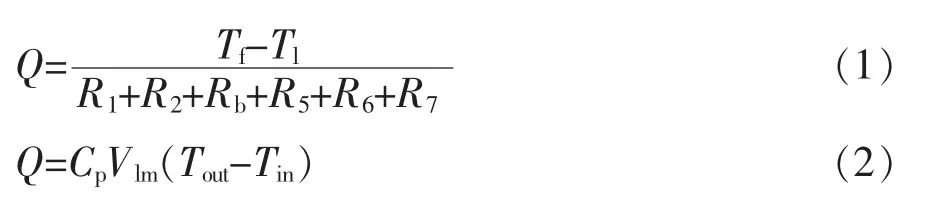
由式（1）、式（2）可知，整个热管的换热量Q可以通过冷却水进出口温度及冷却水质量流量求出，也可由管外热流体的温度Tf与冷却水的平均温度Tl的温差及径向热管的总热阻比求得。在求解过程中Tf，Tin，Vlm为已知变量，需要求解的变量为Tout和Q，而式中R1~R7，Cp均为温度函数，通过对温度的求解算出。式（1）、式（2）封闭，整个传热过程中各项变量可求解。

（1）烟气与外管对流换热热阻

由热管的实际工作情况，可知高温流体与外管对流属于流体横向外掠单管，故外管壁面的Nuf可用丘吉尔与朋斯特[7]提出的准则式计算：

（2）外管壁导热热阻

外管壁导热热阻，可用圆管壁的导热热阻公式[8]计算：

（3）蒸汽与外管壁对流换热热阻

由于管内蒸汽层流运动，属于小雷诺数，利用齐德-泰特公式[9]来计算长L1的管道的平均Nuv数：

（4）液膜凝结热阻

管内蒸气在内管壁面凝结局部表面换热系数，可根据经典努赛尔理论[10]推广得到层流膜状凝结平均表面传热系数计算公式计算：

（5）内管壁导热热阻

（6）冷却水与内管壁对流换热热阻

采用Gnielinski公式[11]计算长L2的管道的平均Nul数：

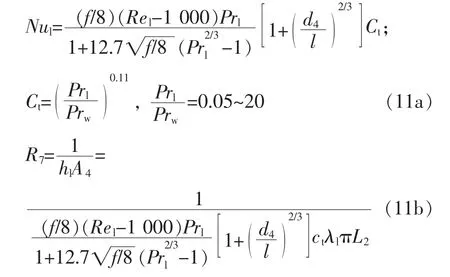
（7）沸腾蒸发热阻

在高功率的工作状态下，将径向热管管内液池的沸腾类比大空间池状核态沸腾[12]，因此对管内液池的沸腾提出两种假设，对应的热阻公式如下：

1）管内液池与壁面核态蒸发热阻

2）管内液池与壁面膜态蒸发热阻

管内的工质与外管壁进行热交换，膜态沸腾受热蒸发，对于横管的膜态沸腾[13]，表面传热系数计算式为：

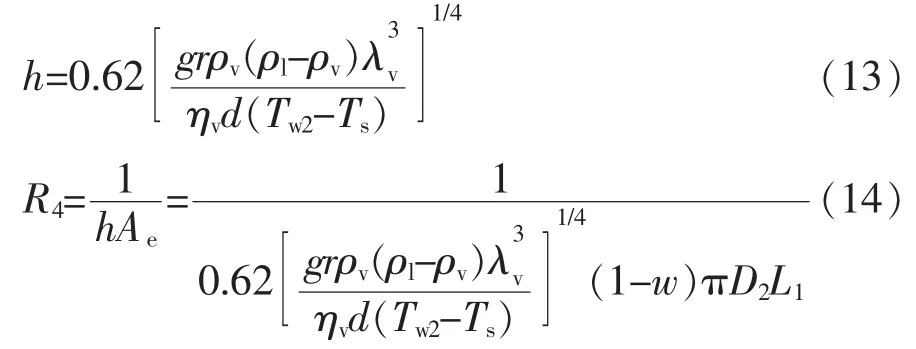
根据上述理论建立模型的计算流程（见图3）。

图3 计算流程图

2 结果分析及模型修正

为与实验结果进行对比，上述液池蒸发换热的两种模型模拟设置的热管尺寸、充液量均与本文之前的实验[14]相同，模拟工况也一致，下述9种工况冷却水进口温度均为283.15 K，其他参数见表1。

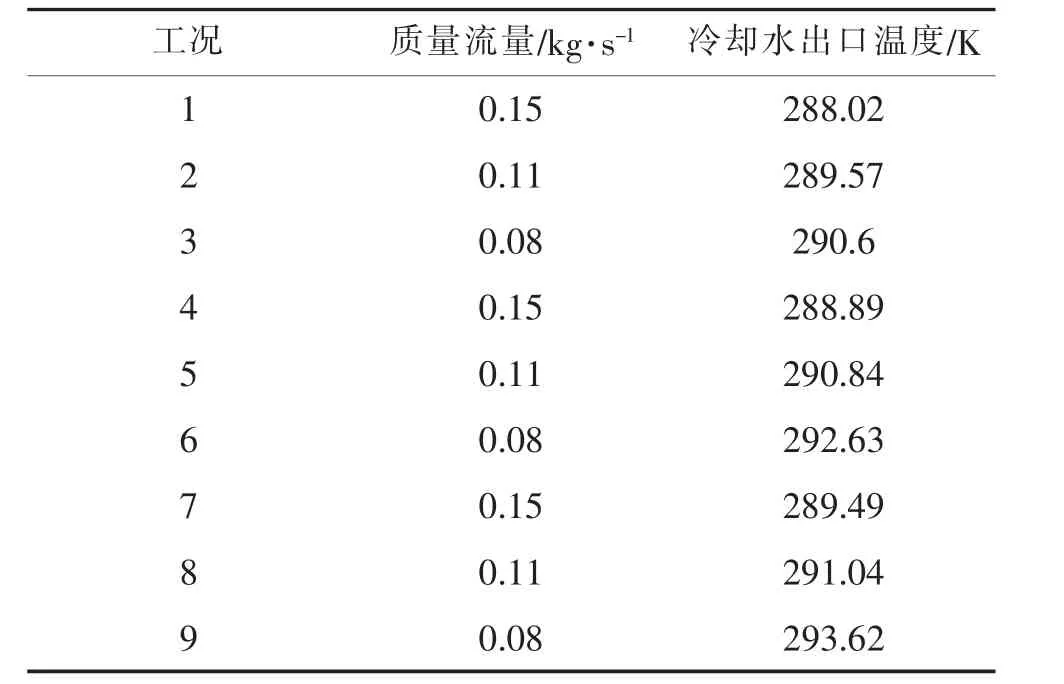
表1 实验工况

实验结果与计算的模拟结果，比较外壁面温度变化状况。图4所示为9种工况下，核态沸腾模型及膜态沸腾模型计算的外管壁温度与实验数据的比较。由图可见，两种模拟结果变化趋势与实验结果相同，表明两种模型均能够合理地反映径向热管内部传热规律，但二者与实验值偏差不同，核态沸腾模型的模拟结果和膜态沸腾计算结果相比更接近实验结果，由此本文将以核态沸腾模型为基础，对其进行修正。通过对比外管壁温可知，热管底部液池沸腾换热系数的实验值介于两种模型之间，即实验工况下沸腾蒸发换热系数小于核态沸腾的换热系数。因此，对核态沸腾的换热系数进行修正，更符合实验情况。

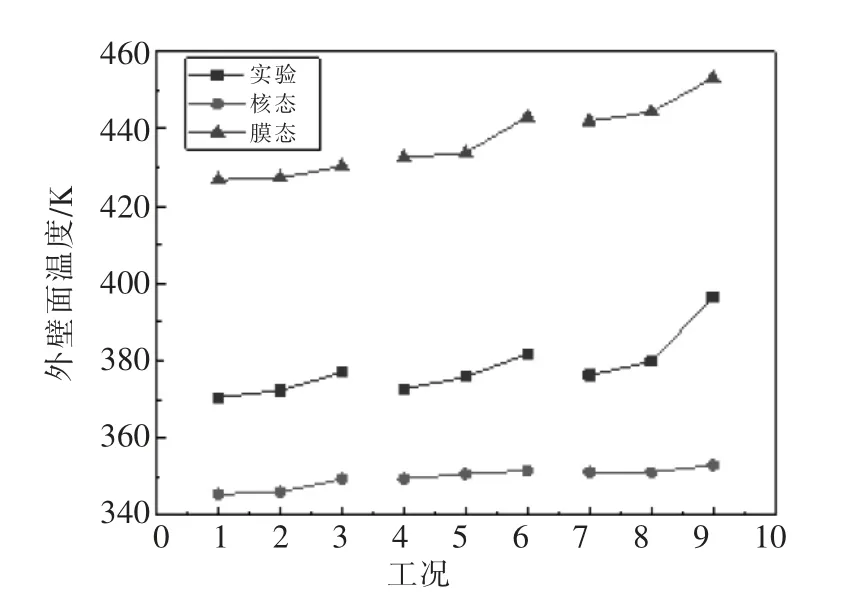
图4 外管壁温度对比图

用核态沸腾模型计算的管内液池沸腾蒸发系数，计算结果与实际管内液池沸腾蒸发系数之间存在一定误差，主要影响管内饱和蒸汽温度；径向热管的管内液池沸腾蒸发的饱和蒸汽低于标准大气压下饱和蒸汽温度T0，饱和蒸汽温度主要影响管内液池沸腾蒸发系数计算。因此选用饱和蒸汽温度用于修正。对核态沸腾换热系数修正基础关系式如下：

由图5（a）可知，9种工况下，换热量相近的每三组工况下，热管的实际沸腾换热系数与核态沸腾模型计算的换热系数存在线性规律；由图5（b）可知，标准大气压下饱和蒸汽温度与热管稳定工作状态下饱和蒸汽温度相比，与图5（a）中两种换热系数比值变化规律相同，通过数学软件进行拟合分析得出常数c=0.529 5，n=0.98，得到修正公式（16）；图5（c）为修正后的沸腾换热系数与热管实际沸腾换热系数比较，可知修正后能较好反映径向热管的实际沸腾换热系数。下为修正后的沸腾换热系数及修正后的沸腾换热热阻公式：

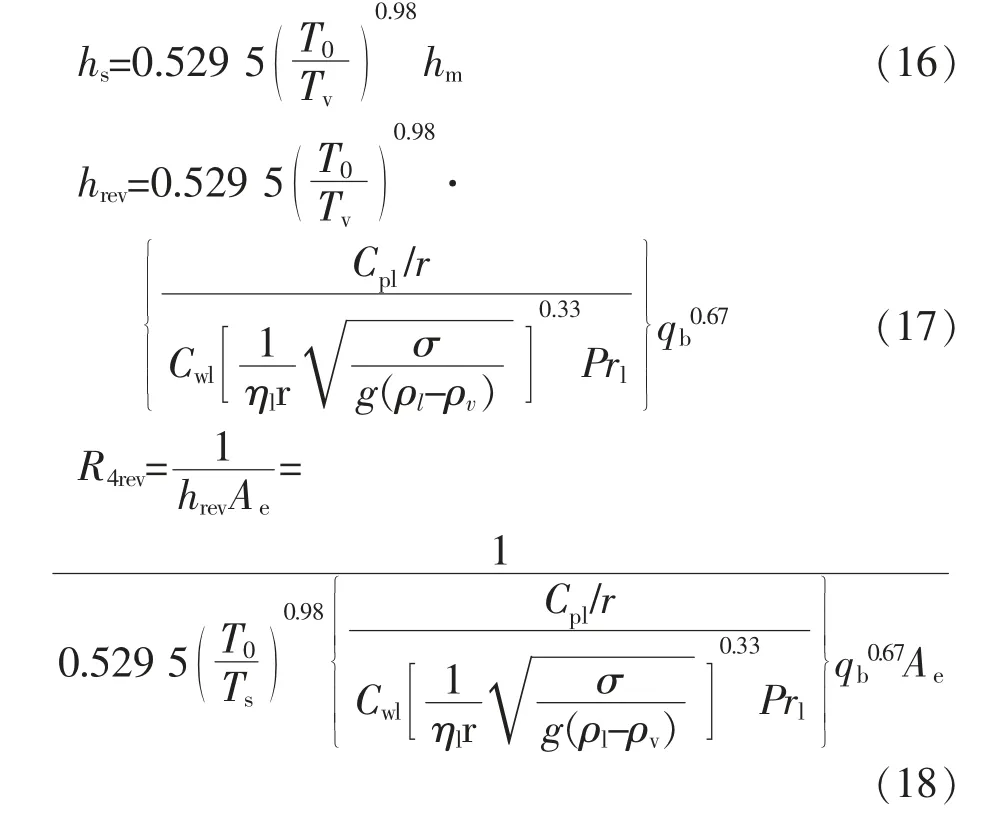
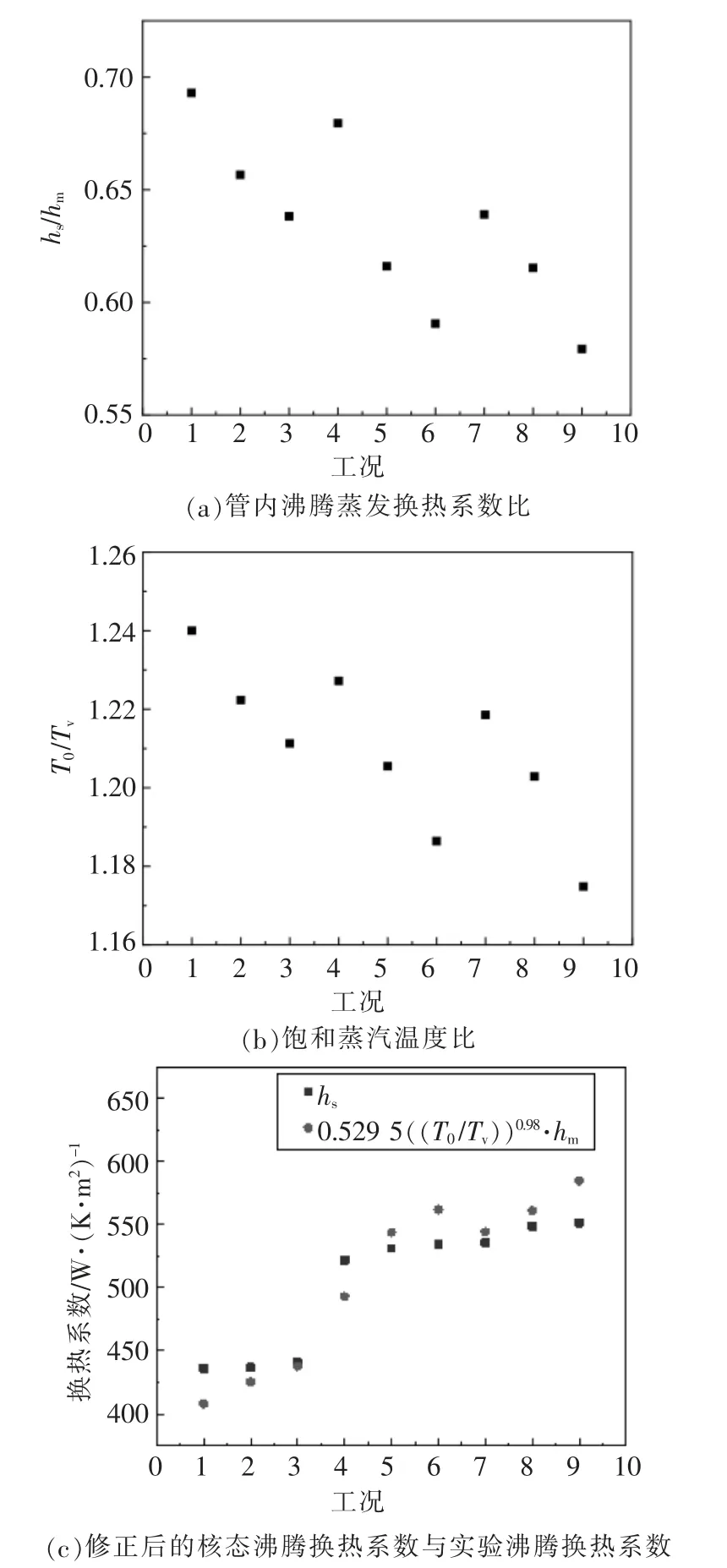
图5 换热系数模型计算值与实验值的对比图

式中，hrev—修正后的沸腾换热系数，W/（m2·K）。

R4rev—修正后的沸腾换热热阻，K/W。

图6为不同工况下外管壁温度两种模型计算结果与实验结果的比较图。直观展现了修正模型计算的外管壁温度与实验数据之间的偏差比核态沸腾模型计算的外管壁温度偏差小。修正后的模型更适合用于计算径向热管的外管壁温度，也更适合计算径向热管的传热过程。表2为三种模型计算的外管壁温度与实验外管壁温度的偏差分析，膜态沸腾模型和核态沸腾模型计算的外管壁温度与实验测得的外管壁温度间存在较大偏差。9种工况中，膜态沸腾模型计算的外管壁温度偏差最大，为14.1%～17.4%；核态沸腾模型计算的外管壁温度偏差为6.23%～10.9%；修正的核态沸腾模型计算的外管壁温度偏差最小，为0.07%～3.37%。其中工况9计算外管壁温度与实验温度偏差最大。综合9种工况，修正的核态沸腾模型在低质量流量（0.08 kg/s）工况下，计算外管壁温度偏差较大，修正模型还存在修正空间。在实际工况中，模型计算偏差在5%以内是可接受的偏差范围。故修正的核态沸腾模型更适合径向热管的换热计算，可用修正后的模型计算径向热管的换热过程。

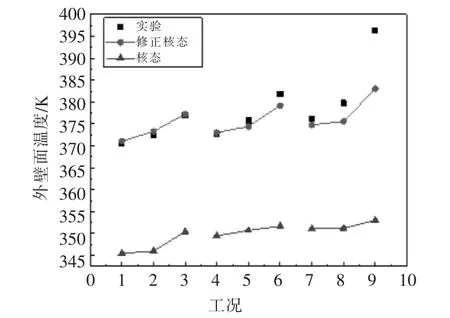
图6 两种模型计算的外管壁温度与实验外管壁温度对比图

表2 三种模型计算的外管壁温度偏差 （%）

3 结论

通过两种不同沸腾蒸发模型计算的外壁温度与实验数据对比，分析得出径向热管管内沸腾换热系数介于两种沸腾换热模型之间。通过对核态沸腾模型进行修正，修正模型计算的管外壁温度与实验结果的偏差小，且趋势一致，故修正后的模型更适合径向热管计算模型。

符号表：

A—对流换热面积，m2

C—系数

Cpl—液体比热容，J/（kg·K）

Ct—修正系数

Cp—定压热容，J/（kg·K）

Cwl—加热表面-液体组合情况的经验常数，Cwl=0.013 0

d—当量直径，m

D—管径，m

f—管内湍流流动的Darcy阻力系数

g—重力加速度，N/kg

h—对流换热系数，W（m2·K）

L—管长，m

m—质量流量，kg/（m2·s）

n—系数

Q—总换热量，W

qb—沸腾热流密度，W/m2

R—热阻，K/W

S-体积质量源，kg/（m3·s）

r-汽化潜热，J/kg

T—温度，K

Vlm—冷却水质量流量，kg/s

w—充液率，%

αv—体积膨胀系数，K-1

λ—导热系数，W/（m·K）

η—动力粘度，Pa·s

θ—角度，°

ρ—蒸气密度，kg/m3

σ—液体-蒸气界面的表面张力，N/m

Nu—努赛尔数

Re—雷诺数

Pr—普朗特数

Gr—格拉晓夫数

下角标：

1,2—与R组合表示过程，其他均为位置

b—并联

e—蒸发段

c—冷凝段

f—热流体

in—进口

l—液相

m—核态沸腾

out—出口

rev—修正

s—实验

t—碳钢

v—蒸汽

w—壁面