多人合作博弈的核心解、应用及其启示——兼论“分配正义”的哲学阐释

杨召富，郭佳宏

（北京师范大学 哲学学院，北京 100875）

博弈包括合作博弈和非合作博弈。历史上，合作博弈先于非合作博弈产生，但前者的研究对象相对于后者而言有些烦琐，相关研究发展相对不足。区分二者的关键在于，在博弈过程中是否存在博弈方使用具有约束力性质的协议。非合作博弈是研究博弈参与者如何在博弈中运用策略使自身利益最大化的博弈。但这通常会造成个体理性与集体理性之间的冲突，导致类似囚徒困境现象的产生，继而达不成和谐的状态和整体利益较好的局面[1]。而在现实生活中，诸多个体通常会合作，他们会联合在一起组成小团体或集团，这种基于博弈方允许存在约束力的协议而形成的博弈称为合作博弈。与其说合作博弈的收益分配或成本分担的解是数学问题，不如说它是经济或社会问题[2]。

从方法论的角度讲，多人合作博弈又称联盟（coalition，也有译成“联合”的）博弈，是指博弈参与人之间建立具有约束力协议的联盟性质的博弈。博弈参与人之间能够形成联盟的原因在于，联盟给个人带来的价值超过个人独自完成某项任务时创造的价值，从而实现共赢[3]。同时，联盟后的利益分配也要彰显正义，保护弱势群体的利益，这样的社会资源分配才是合理的，且有利于联盟的稳定。而这也与儒家学派思想家荀子的“义分则和”思想有着某种相似的旨趣。当然，联盟的形成绝非易事，并且有的联盟具有不稳定性，易被破坏或者瓦解，从而造成资源的浪费。所以，在联盟博弈中，对联盟如何形成、怎样确保已有联盟的稳定性等问题的充分研究是运用联盟博弈恰当分析社会问题，帮助更多人群走出博弈困境、提升团体和社会的公平程度甚至构建和谐美好社会的关键。

一、联盟博弈的相关要素[4]305-306

为了准确地理解联盟博弈的核心解这一概念，我们首先需要了解联盟、协议、联盟值等概念。

联盟：现实社会中的博弈中参与人往往不止一个，而是由多个参与人组成的一个或多个集合体，这种集合体在博弈论中被称作联盟。

协议：协议是联盟各个成员主体商议后的成文或不成文的各项规定，重点是联盟的利益分配。联盟中的每个利益相关者在一定条件下遵循他们之间约定的协议，从而展开竞争与合作。

联盟的个数：假设有n（n为正整数）个博弈参与人，他们构成一个集合N=｛1，2，…，n｝。博弈中的所有可能联盟S的个数为集合N的子集的个数，即2n。S包含四类联盟，分别是：空联盟 ，即没有任何博弈参与人的联盟；大联盟N=｛1，2，…，n｝；单人联盟（不是严格意义上的联盟）｛1｝，｛2｝，｛3｝，…；一般联盟｛1，2｝，｛2，3｝，｛1，2，3｝，｛1，2，3，4｝，｛2，3，4，5｝，…。

可行分配集：分配（也叫效用分配）概念在联盟博弈中至关重要，它关系一个联盟形成后能否持续和稳定，通常用向量x=（x1，…，xn）∈Rn（R表示实数集）来表示，其中xi表示博弈参与人i在联盟中的期望收益。而联盟博弈的可行分配须同时满足个体理性和集体理性两个要求。个体理性意味着，对于联盟内部而言，博弈参与人i在某个联盟中的得益大于等于不参加任何联盟的得益，这对单个博弈参与人有激励性。集体理性则是指，联盟形成后，不仅每个博弈参与人的收益不会比联盟前的少，所有的博弈参与人恰好将联盟形成后的收益分配完毕，此时也称这个分配是有效的。这是针对整个联盟来说的，此时可实现帕累托最优[5]。同时满足上述要求的分配集合被称作联盟博弈的可行分配集，也被称作联盟博弈的“解”。

特征函数（characteristic function）：在具有合作性质的联盟博弈中，用特征函数来表示博弈的局势。特征函数是基于联盟博弈中形成的联盟而建立起来的，也是反映联盟形成的条件和价值的重要概念。其定义如下：设联盟博弈是由n（n为正整数）个博弈参与人组成的集合N=｛a1，a2，…，an｝，∀S⊆N，其中S为博弈中的任意联盟，即S∈P（N），不管联盟外的博弈参与人如何行动，联盟中的博弈参与人之间通过遵循具有约束力的协议可以得到的最大联盟总收益，记作v（S）。在很多情况下，一个联盟能获得的收益依赖于其他人所采取的行动。v（S）有时被解释为联盟S独立于联盟N-S的行动可保证的最多收益[6]。而集合N中的所有可能联盟收益v（S），构成P（N）→R（R表示实数集）的一个实值函数，这个函数被称作此联盟博弈的特征函数。其中，v是从N的幂集到R的映射，S在N的幂集里变化。我们用特征函数来表示联盟值。

二、联盟博弈的解之一——核心

吉利斯在1959年提出了联盟博弈的解——“核心”[7]这一概念。谢识予、熊义杰、潘天群等学者对“核心”这一概念做了深入的研究。

每个博弈参与人在缔结某个联盟时都会关注自己能够在联盟后分配到多少效用或收益。谢识予认为，联盟博弈的解实质上是指在确定了何种类型的联盟形成之后联盟成员如何恰当地分配联盟收益的一种理论[4]365。

为了更好地理解“核心”这一概念，我们引入熊义杰的“优超”这一概念。

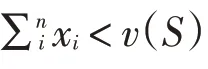
例2：一项任务需要a1、a2、a3三人共同完成，但单独行动或任意两人的联盟都不能顺利完成该项任务。规定完成该项任务的总收益为110。那么此联盟博弈的特征函数可以表示为：v（｛a1｝）=v（｛a2｝）=v（｛a3｝）=v（｛a1，a2｝）=v（｛a2，a3｝）=v（｛a1，a3｝）=0，v（｛a1，a2，a3｝）=110。可见，在上述联盟博弈中，大联盟能够改进任意一个单独联盟或普通联盟。

潘天群指出，在一个N人联盟博弈中，某个效用配置xi在联盟的核心中，当且仅当这个配置xi满足：它对大联盟S来说是可行的，同时不存在比N小的联盟能对配置xi进行改进，即效用配置xi在“核心”中的充要条件为[9]：

从上述条件中可以看出，核心中的分配不仅满足个体理性，而且满足联盟理性，即任何联盟的收益都不小于其离开核心的分配而独立出来所能获得的收益[10]。所以，此时大联盟中的某个博弈参与人不愿意否决这个方案而去加入其他的联盟，因为此时的分配给他带来的利益是最多的。

如果一个效用配置xi未在核心当中，那么一定存在某个联盟S，使得联盟S中的博弈参与人之间通过共同合作、分配v（S）而使他们获得严格高于效用配置xi的支付或收益。

上述例2的核心为｛a|a1+a2+a3=110，a1≥0，a2≥0，a3≥0｝。显然，如例2的核心所显示的那样，核心通常是一个解集，它往往不能给我们提供唯一的解。甚至，联盟博弈的解有时可能是空集。比如，某个联盟博弈的特征函数可以表示为：v（｛a1｝）=v（｛a2｝）=v（｛a3｝）=0，v（｛a1，a2｝）=v（｛a2，a3｝）=v（｛a1，a3｝）=0，v（｛a1，a2，a3｝）=100。它的解就是空集。

核心只是表明什么样的分配是稳定的，不能解决对于解的多样性和不存在性这两类问题，这也是它作为联盟博弈的解概念的缺陷之处[4]366。当然，这种缺陷并不能否定核心这一概念在帮助人们理解联盟博弈时的用处。

三、联盟博弈核心解的应用

核心是多人合作博弈出现的最早的解概念，这样的解对于博弈参与人个体而言是相对公平的，对于所有博弈参与人组成的大联盟而言也是最优的。

（一）“塔木德分配方案”谜题[11]

《塔木德》是一部用于规范古代犹太人生活行为准则的重要法典，记载了一个关于婚姻契约与财产纠纷的故事。契约规定，如果出现婚姻中止（离婚或者死亡）的情形，男方要给予女方一定的经济赔偿。一个犹太男子娶了3个妻子（分别为1、2、3），没过多久不幸死亡。而契约上约定给妻子1、妻子2、妻子3的财产分别为100、200、300。但是，这个男子死后并没有留下足够遗产。三个妻子为了争夺男子的遗产，就请犹太拉比们根据男子实际留下的遗产给予一个公平的分配方案。《塔木德》一书中记载了犹太拉比们最终裁决的关于三个妻子分配遗产的解决方案，见表1。

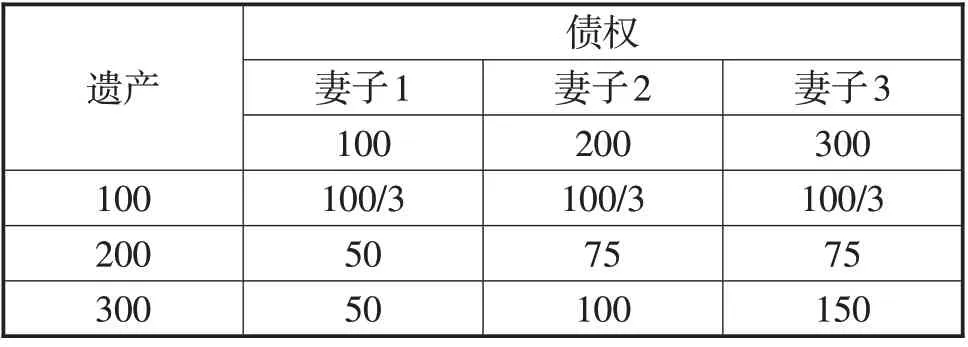
表1 三妻争财产问题的塔木德解决方案

按照常理，这三个妻子得到遗产的比应该是1∶2∶3。但从上表中得知，仅当男子留下的财产达到300时，上述方案中的分配比例才会成立。上表中的数字具体是如何分配的困扰了很多人，这个分配方案的依据与合理性成了一个千古谜题。直到1985年，两位博弈论专家奥曼和马希勒成功地破解了这一难题[12]，经过研究发现，解开这个谜团的钥匙就在《塔木德》法典的开头部分。《塔木德·损害部·中门卷》第一章第一节的“争执大衣原则”为三妻分财产的分配方案提供了合理的解释：

两人抓着一件大衣，来找拉比裁决：如果两人都认为自己拥有这件大衣的全部所有权，拉比会裁定二人平分这件大衣。如果一个人说大衣全是他的，另一个人说大衣的一半是自己的，那么拉比最终裁定第一个人可以得到大衣的3/4，第二个人得到大衣的1/4。

“争执大衣原则”大致包含两个方面的内容[13]：

（1）争执两方仅对有争议的部分进行分配，不考虑无争议部分的分配。因此，声称自己对大衣拥有一半所有权的一方不幸率先失去索要的那半件大衣，只能跟声称拥有全部大衣所有权的一方平分半件大衣，而剩余的半件大衣归第一个人所有。

（2）争执过程中，提出较多分配一方的最终所得应不少于提出较少分配的一方。

奥曼和马希勒成功找到以上两条原则之间的关系，在他们合著的论文中得出了重要结论：塔木德分配方案是唯一一个与争执大衣原则相一致的解决方案[12]。

再回到三妻分遗产的例子。当遗产为100时，根据“争执大衣原则”，三个妻子都有权获得全部遗产，该结果没有争议，所以分配为（100/3，100/3，100/3），与塔木德分配方案的结果完全相同。当遗产为200时，其中100是没有争议的，所以妻子1没有资格获取这100遗产。这时我们需要将分配方法转换成联盟博弈。根据“争执大衣原则”，妻子2和妻子3可以结成一个联盟，获得这100。随后，这个联盟再与妻子1分剩余的100。此时，妻子1分得50，妻子2与妻子3共分得150。对于这150，妻子2和妻子3是没有争议的，应均分，各得到75。（50，75，75）就是三个妻子的最终分配。

同理，当遗产为300的时候，运用“争执大衣原则”，可以得到最终的分配为（50，100，150）。

（二）塔木德分配方案的核心解博弈分析及其启示

将“争执大衣原则”推广后得到的分配方案即为塔木德分配方案，而《塔木德》法典里许多问题的解决都凸显出恰当运用联盟博弈的核心概念可以成功解决现实问题。经研究发现，《塔木德》法典给出的所有遗产分配方案中的每个解均在博弈的核心里，所以那些解都是合理的。比如，当犹太男子遗产很少，并且假定他的三个妻子又都依靠他的遗产过活，此时如果按照1∶2∶3的比例来分配财产，原本就处于劣势的妻子1会分得的财产太少，或许没过多久生活就会陷入窘境。而《塔木德》法典中的分配方案很好地改善了这一状况。

上述遗产分配问题涉及联盟博弈的核心问题。当财产为100时，假定每个妻子的分配是（100/3，100/3，100/3），那么该分配方案没有争议。但是，诸如（30，30，30）这样的分配方案是不会被接受的。原因在于，这三个数字之和小于100。也就是说，这样的分配是不稳定的，至少会被其他方案所改进。例如，方案（33，33，34）对于方案（30，30，30）来说，就是改进的。

当遗产总数是100时，该博弈的核心是｛a|a1+a2+a3=100，a1≥0，a2≥0，a3≥0｝，而法典中记载的分配方案（100/3，100/3，100/3）包含在核心当中。

当遗产总数是200时，此时博弈的核心是｛b|b1+b2+b3=200，b1≥0，b2≥0，b3≥0｝。当遗产总数增加到200时，每个妻子分得的财产应该不少于遗产总数是100时分得的财产，即须满足条件：b1≥a1，b2≥a2，b3≥a3。可以看到，被建议的分配方案（50，75，75）在核心中。

同理可以得出，当遗产总数为300时，被建议的分配方案（50，100，150）也在此时联盟的核心当中。

由此可以看出，《塔木德》法典中所有的分配方案均在博弈的核心之中，符合联盟博弈关于如何分配联盟成员间利益的理论。

塔木德分配方案与当今社会中的重大经济问题之一——破产问题的解决方案有着内在的一致性，它为破产争执这类经济问题提供了很好的借鉴方案[14]。在现实生活中，企业在发展过程中由于资不抵债而被迫依照法律程序宣告破产，由专门机构对企业的剩余资产进行清理和评估，然后将评估后的资产一定程度上分给企业的各个债主。当然，企业偿还给债主的财产不一定能够补偿他们的债权。企业的剩余资产通过清理而最终被全部分割。在给企业的各个债主分割财产这一事情上，法院通常不会根据“比例”均分剩余资产，法院会根据各个债主提供的理由对其进行赔偿。所以说，法院对宣告破产企业的财产完全进行分割后偿还给企业的债主，这与《塔木德》中三个妻子全部分割丈夫的遗产的情形和逻辑思路完全一致。

从博弈论的视角看，《塔木德》分配方案实质上是多人合作博弈的一个核心解。它的独特之处在于，此方案一以贯之地保护了弱势群体的利益。如果争执方接受这一准则，那么在分配争执过程中，任何一方从任意角度出发均会发现这样的分配方案都是公正的。实际上，塔木德案例所体现出来的分配原则更符合现代社会所提倡的和谐意识，更能反映现代社会所需要的均衡理念，因此显得既公平又合理[11]。现今，多人合作博弈的核心解与古典塔木德分配方案的思想不谋而合，保护弱者利益，体现出分配的公平和正义，有深刻的哲学意蕴。

四、多人合作博弈核心解的哲学阐释

分配的正义问题，在中国的儒家思想和美国新自由主义学派的代表人物罗尔斯的《正义论》中均有所体现。荀子：“人何以能群？曰：分。分何以能行？曰：义。故义以分则和。”（《荀子·王制》）这是“义分则和”思想的直接来源。荀子所处的时代正处于社会的转型期，社会中的各种力量冲突不断，社会资源如何公正地得到分配，是荀子面临的时代课题。荀子的“义分则和”思想表达的主要还是“和”的愿望和理想，具有很强的现实性。荀子的“分”含义广泛，是包括人、行事和财富的一种大分配观念。这里的“分”专指荀子对诸如财富等社会资源的分配。在荀子看来，“分”具有可行性。“分何以能行？曰义，故义分则和”（《荀子·王制》），即通过“义”来保证“分”的可操作性。具体来说，借助“礼义”，即“道德和制度”来进行分配。荀子在阐释“礼”的渊源时说：“礼起于何也？曰：人生而有欲，欲而不得，则不能无求。求而无度量分界，则不能不争；争则乱，乱则穷。先王恶其乱也，故制礼义以分之，以养人之欲，给人之求。使欲必不穷于物，物必不屈于欲。两者相持而长也。”（《荀子·礼论》）可见，在荀子的时代，他主张通过“礼”来安定社会的秩序，通过“礼”来对有限的社会资源进行合理的分配。而对于新时代而言，需要合理的顶层设计来保证资源分配的公平和正义。所以说，荀子的“义分则和”思想对于新时代的分配制度的设计以及和谐社会的构建具有启发性。这里的“公正”需要从制度伦理的角度来看，即将道德的公正与制度的正义相结合。换句话说，和谐社会的建构需要合理的分配制度作为前提，在道德和制度两个层面上有所建树，从而对稀缺的社会资源进行合理的分配。罗尔斯在《正义论》的开篇中说过：“正义是社会制度的首要价值，正如真理是思想体系的首要价值一样。”[15]分配正义是和谐社会的价值原则和基本目标，是社会主义和谐社会的题中之义[16]。改革开放40多年来，我国的分配制度与分配正义原则的精神相契合。富裕群体最大限度地享受了改革开放发展的红利，实行分配正义原则之后，他们仍然会是受益者。这种原则受“帕累托改善”①的制约，富裕群体的社会福利水平不会因此而降低。由于各个社会群体在利益上存在链式效应，分配正义原则的实行在改善弱势群体福利的同时，富裕群体的福利也会随之提高。所以，“人们就正义原则达成一致，不是因为每个人都有理由接受它，而是因为任何人都没有理由拒绝它”[17]。

五、结语

多人合作博弈中的“核心”概念，使博弈参与者找到了相关博弈参与人的利益均衡点，也使人们在处理现实社会中的一系列经济纠纷问题（如家庭的遗产继承、企业的破产决算等）时更具有人文关怀[18]。一方面，在资源较少时，平均或接近平均分配，能有效保护弱势群体的利益。对弱势群体、边缘人群的关怀及尊重体现出来的博爱精神，不仅适应现代社会乃至人类发展的道德要求，也是传统人格平等观念以及儒家孟子人性观的四端之首——恻隐之心的必要引申[19]。“正义是对弱者生存权利的关注和对强者权利意志的约束。”[20]另一方面，当资源比较丰富时，将超出博弈参与人所需资源的剩余部分集中起来，为实现更大规模的再分配打下良好的基础，这也体现出博弈规则对于每个博弈参与人权利保护的公正性和科学性。核心解体现出的分配思想与罗尔斯的分配正义思路基本上是一致的：“能平等分配的东西都应该平等分配，不能平等分配的东西应该实行差别原则②——应该有利于最不利者。……收入和财富做不到人人平等，那么根据差别原则，它们的不平等分配只有符合最不利者的利益，才能够是正义的。”[21]这种分配的基础是公平而不是平均，它能够激励强者，更能让弱者感觉到公平的存在，能够在最大限度上调动博弈参与人的积极性和实现重复合作的可能性。从更加宏观的角度来看，联盟博弈中的核心解体现了博弈思维的智慧性和人性化。所以，世界性、区域性组织的权力代表在制定分配机制设计方案时灵活运用博弈核心解的相关理论，能够从全局和实际出发，充分认识到保护弱者利益的重要性，减少或消除潜在的社会矛盾，实现双赢甚至多赢的局面，为社会的和谐乃至人的全面发展作出长远打算。需要注意的是，本文只是用核心解这一概念解释了一些社会经济现象，但从概念的解释、制度的制定再到制度的实施，还需要法律（立法、执法）来加以保障；同时，现实情形中的经济分配问题情形较为复杂，使用核心解或许不能很好地解决诸如塔木德法典中的三妻争财产问题（如出现解为空集或反例的情形），所以我们需要在理论上对联盟博弈的核心解加以拓展，这是下一步的工作。

注释：

①帕累托改善（Pareto improvement），也称帕累托改进或帕累托优化，是基于意大利经济学家帕累托（Vilfredo Pareto）的名字来命名的，是指将现状分配方案A与将要施行的分配方案B进行比较，在施行B方案之后，在没有使任何人的状况变得糟糕的情形下，一些人的状况得到了改善。参见姚大志：《分配正义：从弱势群体的观点看》，《哲学研究》2011年第3期。

②差别原则（difference principle），又称最大化最小原则（maximin principle），是罗尔斯《正义论》（1971）中极具代表性的思想观点。该原则认为，在公平平等的程序正义的基础上，社会成员在经济上的不平等须对社会中的最不利群体或成员有利。从本质上说，该原则彰显一种人文关怀，欲借助于社会制度来最大限度上缩小贫富差距，通过制度将不平等限制在可接受的范围之内，旨在建立一种互利互惠的维系社会合作的体系。参见贾中海：《社会价值的分配正义——罗尔斯自由主义政治哲学批判》，中国社会科学出版社2011年版，第29—43页。