一种基于MRF与区域合并的图像分割改进算法

王国良，任允帅

一种基于MRF与区域合并的图像分割改进算法

王国良，任允帅

（辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001）

针对现有基于马尔科夫随机场的图像分割算法容易出现过分割、分割结果不理想等问题，提出了一种基于马尔科夫随机场与区域合并的图像分割改进算法。该算法首先基于马尔科夫随机场与高斯混合模型理论的图像分割算法得到初始分割结果；然后利用各个区域间的相邻关系、颜色关系以及边界情况等信息，给出各个区域间的距离；最后按照区域间的距离与区域合并前后的颜色散度变化率对初始分割结果进行区域合并，输出最终的分割结果。使用伯克利标准图像库进行实验仿真，采用Dice系数和Jaccard系数作为评价指标。仿真结果表明，相比于现有基于MRF理论的算法，本文算法具有更好的分割效果。

图像分割； 马尔科夫随机场； 高斯混合模型； 区域合并

图像分割是图像处理领域的热门问题，是计算机对图像进一步处理的关键步骤[1]。图像分割是将图像划分为多个具有某种特定性质的子区域的过程，相同的子区域间具有相同或相似的物理特性。目前常用的图像分割方法有阈值分割法、区域分割法、聚类分割法和基于某种特定理论的图像分割算法等。

基于-means的图像分割算法是一种聚类分割的算法，其原理简单，容易实现，被广泛应用于图像分割[2-4]。但是,这种无监督聚类分析法在聚类时未考虑图像的空间信息，分割结果易受噪声点影响。为解决噪声点的问题，通常加入特定的方法对-means算法进行约束[5]。马尔科夫随机场（MRF）模型[6-13]具有严格的理论基础，在图像分割领域得到广泛的应用。MRF理论本身不具有分割作用，但可以与特定的分割算法相结合。MRF理论的引入为-means算法带来空间约束性，提高分割算法的抗噪性能。近年来，MRF理论在图像分割领域快速发展。徐迪[12]提出使用模拟淬火法的马尔科夫分割算法，解决马尔科夫图像分割算法的局部最优解问题。祖成玉[13]提出基于邻域统计的MRF图像分割算法，通过改变马尔科夫随机场模型，一定程度上解决了图像分割中的过分割现象，但也因此增加了分割算法的计算难度。

由于图像中各个区域之间存在相似的物理特性，现有常用的基于-means和MRF理论的图像分割算法极易受这些物理相似性的干扰，从而导致分割结果不够理想。针对这个问题，本文提出了一种将MRF理论与区域合并相结合的图像分割算法。首先基于MRF理论的分割算法得到初始分割结果，然后利用区域合并策略对初始分割结果进行修正，输出最终的图像分割结果。相较于对比算法，本文算法可以更好地处理图像分割中的过分割问题，提高图像的分割精度。

1 算法及原理

本文算法主要分为两个部分：初始分割部分，使用带有高斯混合模型的马尔科夫最大后验概率（MRF-MAP）算法得到；区域合并部分，综合考虑各个区域间的相似程度和相邻关系等信息，按照区域合并策略对初始分割结果进行区域合并，最后输出最终的分割结果。

1.1 MRF-MAP算法概述

马尔科夫随机场是基于概率统计的图像分割模型。使用马尔科夫随机场对图像建模时，将直接观察到的实际图像设为观测场，在实际图像对应的位置建立一个标签场，标签场中的标签即是图像分割的结果。

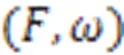
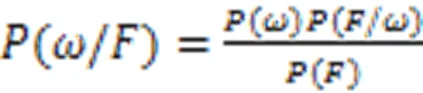
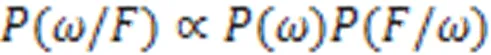
进而图像分割问题转化为式（3）最优化问题：

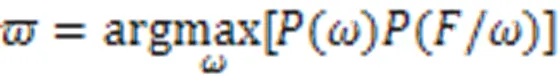
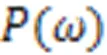
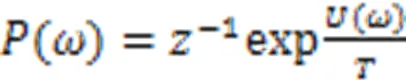
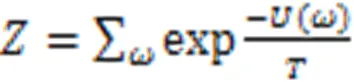
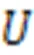
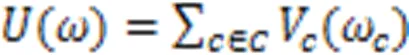
式中，为所有双点势团的集合。

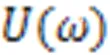
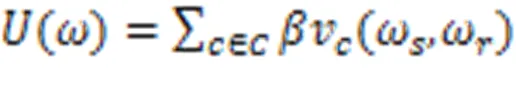
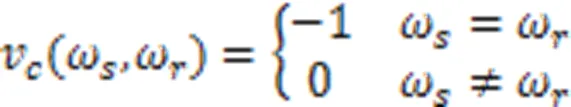
由式（4）、（5）和式（7）可得：

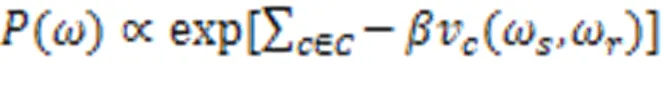
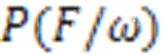
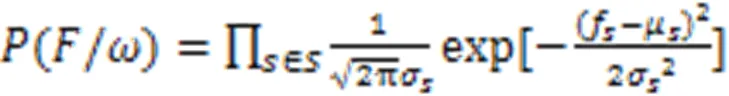
1.2 基于GMM的MRF-MAP算法概述

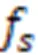
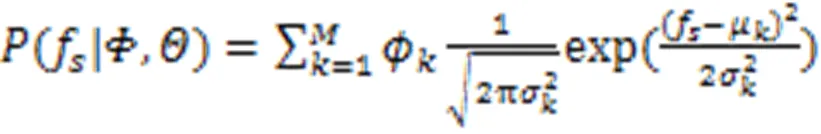
对式（11）取对数，得：

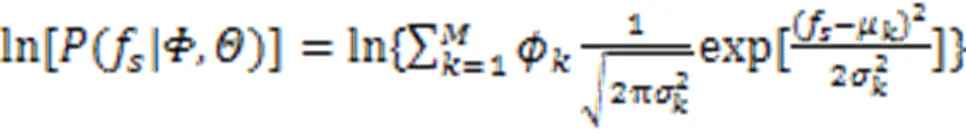
式（12）取得最大值时GMM的参数最优，且满足：

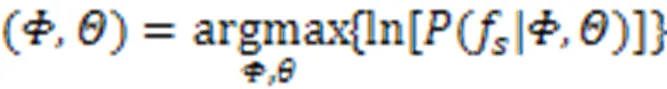
一般情况下使用EM算法估计GMM的参数。使用式（11）高斯混合模型代替单一高斯分布，式（10）可以更改为：

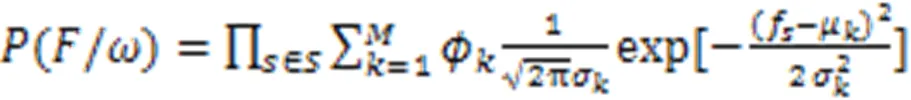
由式（2）、式（9）和式（14）可得：

对式（15）取对数，得：

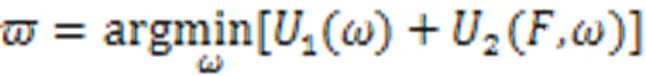
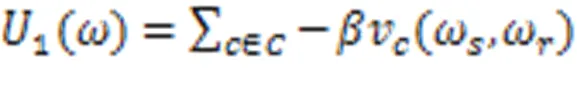
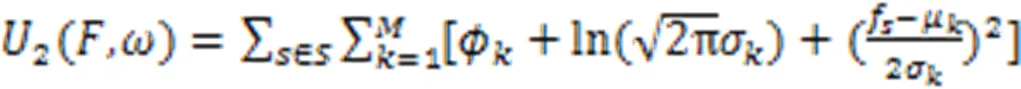
最优化问题被转换成式（16）能量最小化问题。利用标签场能量和观测场能量间的约束关系，根据贝叶斯准则得到分割结果。

GMM的处理对象是观测场的像素值，因此易受噪声点干扰，MRF理论可以刻画各种物理现象的空间相关性，两个理论非常适于结合使用，MRF理论引入先验知识，可以求解先验概率。GMM可以求解似然概率，两者借助贝叶斯理论结合使用。根据最大后验概率求解，即可确定像素的所属标签。

使用MRF和GMM可以得到一个较为精确的分割结果，但是当图像中的干扰区域较大时，分割结果的过分割现象依然存在。单纯改进MRF和GMM的相应参数常会出现减少过分割现象的同时，也破坏了分割目标主体的情况。为此本文引入区域合并思想，从另一种角度来改进分割结果。

1.3 区域合并

区域合并是实现更加精细化图像分割的一种方法，这种方法的优点在于充分考虑区域间的空间位置关系，降低像素值对于图像分割的约束。本文算法借鉴文献[21]的层次合并法对初始分割进行区域合并。

1.3.1区域相似性 区域间的相似性是两个区域进行合并的重要依据[22]，本文采用区域距离对区域之间的相似性进行量化。

在进行区域合并时，两个区域是否可以合并需要考虑两个区域是否相邻，只有相邻的区域才可以考虑合并；两个区域的颜色是否接近，只有颜色接近的两个区域才可能进行合并；两个区域相邻的位置是否存在边界，没有边界的两个区域才可能进行合并。本文依据上述条件来定义区域间的相似性。

（1）为了理清区域间的相邻关系逻辑，建立合理的相邻关系表达式。区域相邻关系如图1所示。

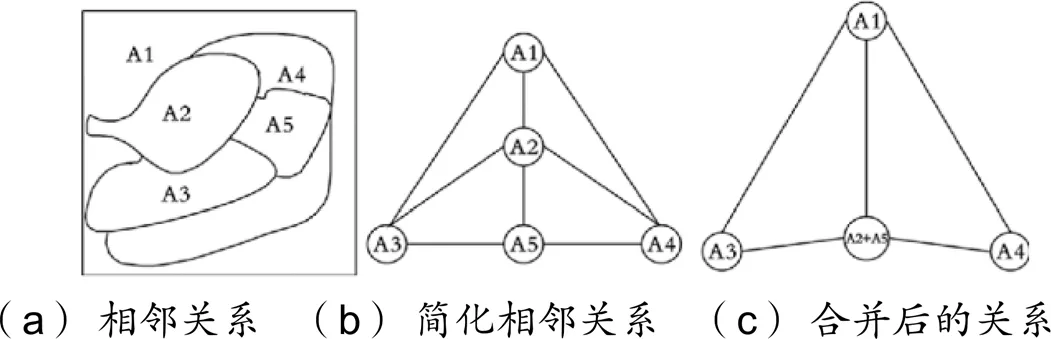
图1　区域相邻关系

图1（a）为图像实际区域相邻关系图，图中区域A1与区域A2、A3、A4相邻。使用短线相连表示区域相邻，得到简化相邻关系如图1（b）所示。当A2和A5满足合并条件，区域合并后可以得到新的相邻关系如图1（c）所示。

通过图（1）中的相邻关系，建立区域相邻关系表达式：

（2）本文定义了一个颜色距离函数，使用颜色距离表明两个区域颜色的接近程度，其表达式为：

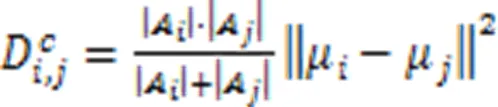
（3）当图像的两个区域间存在边界时，边界两侧的颜色有明显变化。按照这个逻辑，建立一个边界距离关系式为：

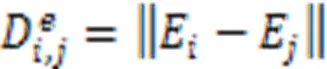
按照上述逻辑关系整合上述三个函数关系式，得到一个综合的区域间距离关系式为：

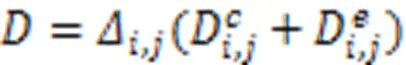
区域间距离越小，表明两个区域间的差异越小，合并的可能性就越大。

1.3.2区域合并策略 使用基于GMM的MRF-MAP算法得到一个初始的分割结果，在初始分割结果的基础上进行区域合并。区域合并的步骤为：

（1）标记区域间的相邻关系。根据相邻关系式（19）可得不同区域间的相邻情况。

（2）减少合并区域的数目。图像经初始分割后，分割结果中容易出现由噪声点引起的面积很小的干扰区域。为减少运算量，可以通过设置一个面积阈值，将面积很小的区域合并到其相邻区域。

（3）计算区域间的距离，合并区域间距离最小的两个区域。区域的数目、区域间的相邻关系和区域间的距离将会在区域合并后发生改变。因此，算法要重新返回到第一步和第二步。合并算法要在第一步到第三步间不断循环，更新分割结果，直到分割算法达到合并截止的条件，结束循环输出最终的分割结果。

1.3.3区域合并截止 设置合并策略后，还需要设置一个合并截止条件。本文使用颜色散度作为合并截止的条件，将图片中不同区域间颜色不统一程度的总和定义为颜色散度，其表达式为：

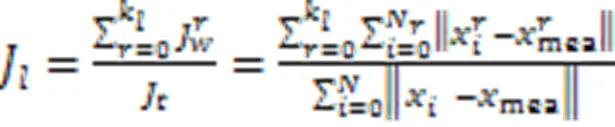
区域合并会改变图像的整体颜色散度。当区域合并前后的颜色散度变化较大时，说明区域合并导致了区域之间的不统一程度加大，应停止区域合并。

只使用颜色散度变化作为停止区域合并的条件不够全面。为此，本文考虑将颜色散度与区域合并后区域的数目相结合，定义一个新的合并截止条件，即颜色散度变化率，其表达式为：

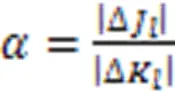
当区域在合并前后颜色散度变化率出现明显时，认为合并算法停止，输出最终的分割结果。

本文算法流程如图2所示。

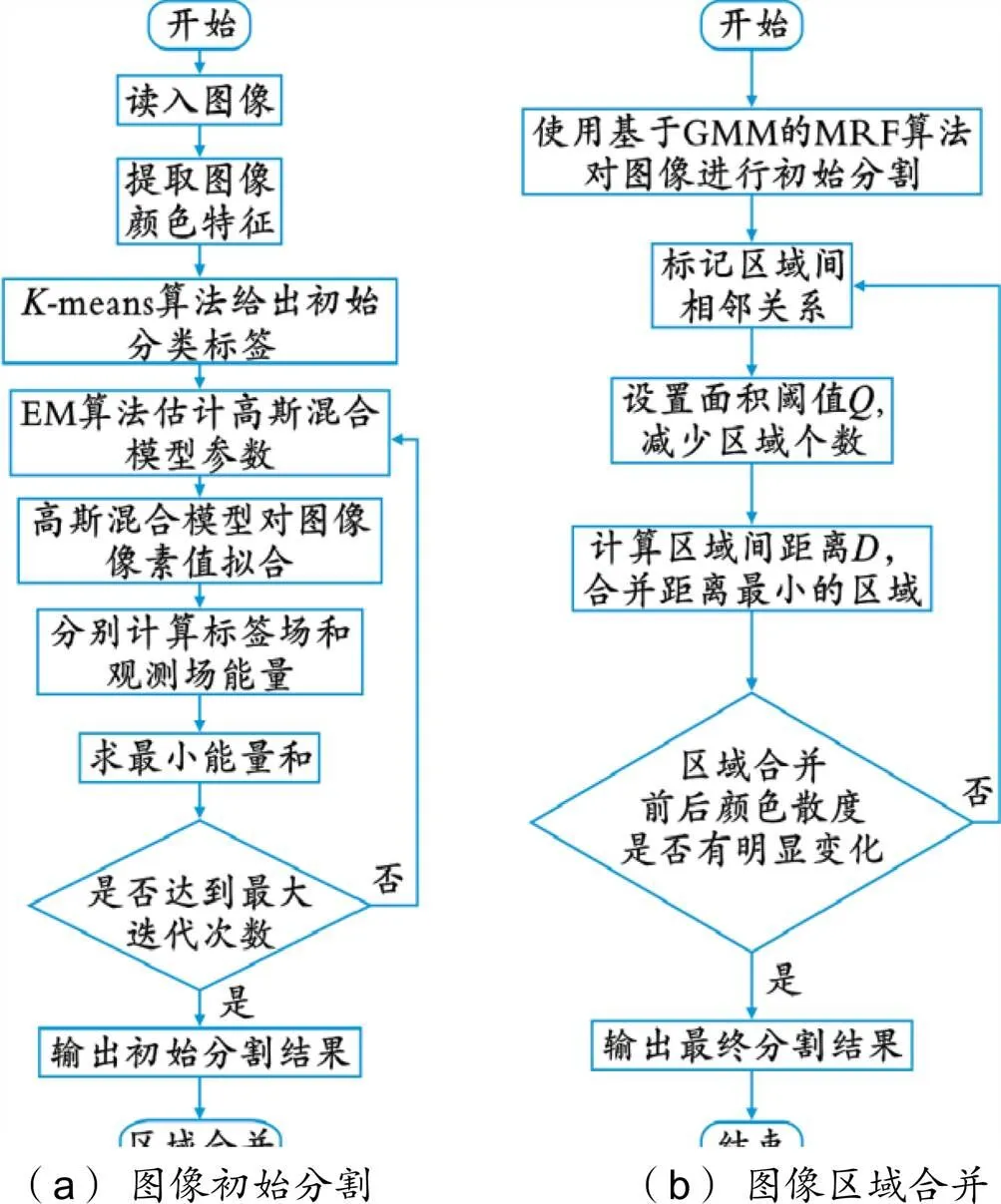
图2　本文算法流程

2 实验与仿真

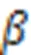
2.1 实验结果对比分析

本文算法与-means算法[3]、传统MRF算法[12]、基于GMM的MRF算法[19]进行仿真对比。海星、双马图像不同算法的仿真结果如图3所示。其中，人工分割为标准分割结果。

图3（b）中，由于海星图草地背景部分像素值接近海星主体，草地背景区出现较大误判情况；图3（c）结果相比于图3（b）海星目标主体得到较为完整的分割，但分割结果中出现很多噪声点，同时其右下角的草地背景过分割加重；图3（d）海星目标主体边缘更加清晰，背景区域的误分割情况减弱，分割图左侧和下方仍有小块区域过分割给海星；图3（e）结果中，本文算法最大程度保证了目标区域的完整性，同时去掉了过分割区域，使分割结果更加趋向于标准结果。双马图与海星图分割结果相似，本文算法分割结果优于其他算法。

使用背景复杂的图像来进一步验证算法的可行性。水牛、青蛇图像不同算法的仿真结果如图4所示。

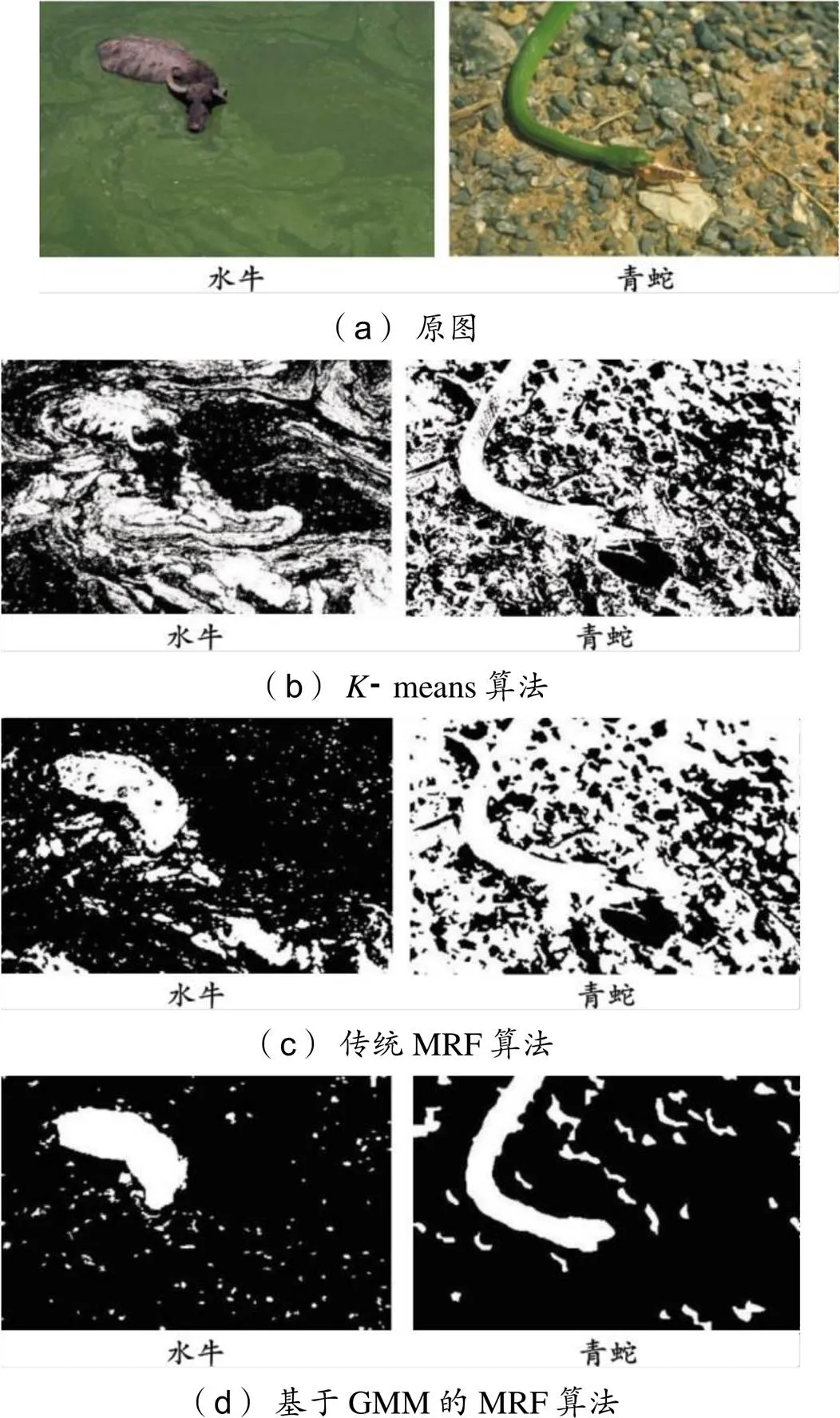
从图4可以看出，由于水牛、青蛇图片背景较为复杂，使用-means算法得到的结果图4（b）受到背景干扰像素的影响，出现了大片的误分割区域。MRF理论的引入带来了空间约束，一定程度降低了噪声点影响，但在图4（c）分割结果仍然存在面积较大的误分割区域和较多的噪声点。图4（d）水牛、青蛇主体的连通性增强，误分割情况减弱，但仍然存在大量难以去掉的误分割区域。与其他算法相比，图4（e）分割结果提高了分割目标主体连通性，去除了其他算法难以除去的噪声点，与人工分割结果最为接近。本文算法结合了MRF和GMM的优点，加入区域合并策略，利用图像颜色散度等概念，进一步消除了图像分割中的过分割区域，提升了算法的分割效果。

2.2 算法性能对比分析

为更加客观地评价本文分割算法的分割性能，使用定量的指标给出精确评价。由于目前图像分割的评价方法尚不统一，本文选用Dice系数[23]和Jaccard系数[24]作为评价本文算法分割性能的指标。

Dice系数是一种集合相似度度量指标，用于计算两个集合间的相似度，取值为0～1。分割结果最佳时取1，结果最差时取0。Dice系数的表达式为：

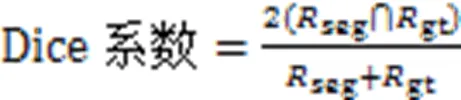
Jaccard系数是衡量两个集合之间区分度的度量指标，与Dice系数相似，Jaccard系数越大，两个样本就越相似。Jaccard系数的表达式为：

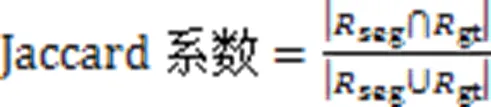
海星、双马图像不同算法的评价结果如表1所示。从表1可以看出，-means算法得到的结果与人工分割结果（Dice系数、Jaccard系数均为1.000 0）相差最大，分割效果最差。使用MRF理论与高斯混合模型的图像分割算法，Dice指标和Jaccard指标相比-means算法都有较大的提升，这也说明了MRF理论和高斯混合模型结合使用对于图像分割起到了重要的作用。加入区域合并策略的本文算法与其他算法相比，无论是Dice系数还是Jaccard系数都是所有分割算法中最高的，这说明本文算法得到的分割结果与人工分割结果最为接近，分割效果最好。

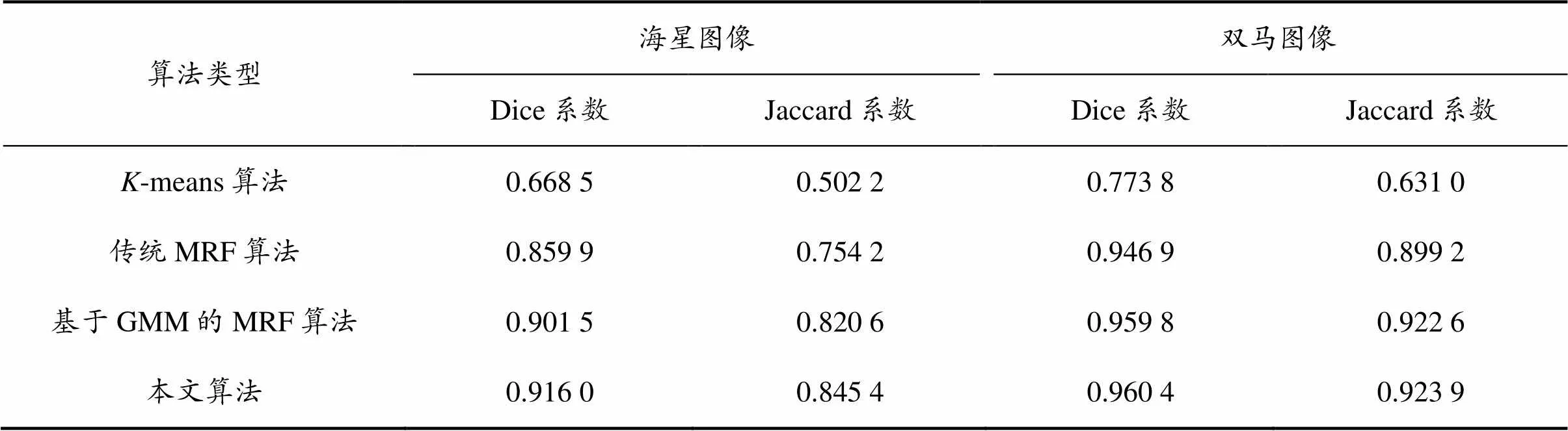
表1　海星、双马图像不同算法的评价结果

水牛、青蛇图像不同算法的评价结果如表2所示。从表2可以看出，除本文算法外其他算法都不能很好地将目标主体从背景中分离，本文算法的Dice系数和Jaccard系数最大，相比其他算法，本文算法的Dice和Jaccard数据增幅明显。这表明本文算法的分割效果优于其他算法。

3 结 论

基于马尔科夫随机场与区域合并的图像分割改进算法，使用高斯混合模型的高斯分量进行像素值拟合，对观测场建模；使用马尔科夫模型求解先验概率，对标签场建模。利用贝叶斯准则将高斯混合模型与马尔科夫模型相结合，得到初始分割结果。利用区域合并的思想对初始分割结果进行更新修正，输出最终的分割结果。由于Markov和区域合并的空间约束性，一定程度上改进了现有MRF算法的过分割现象。该算法的分割结果与人工分割结果最为接近，这也验证了本文算法的可行性。

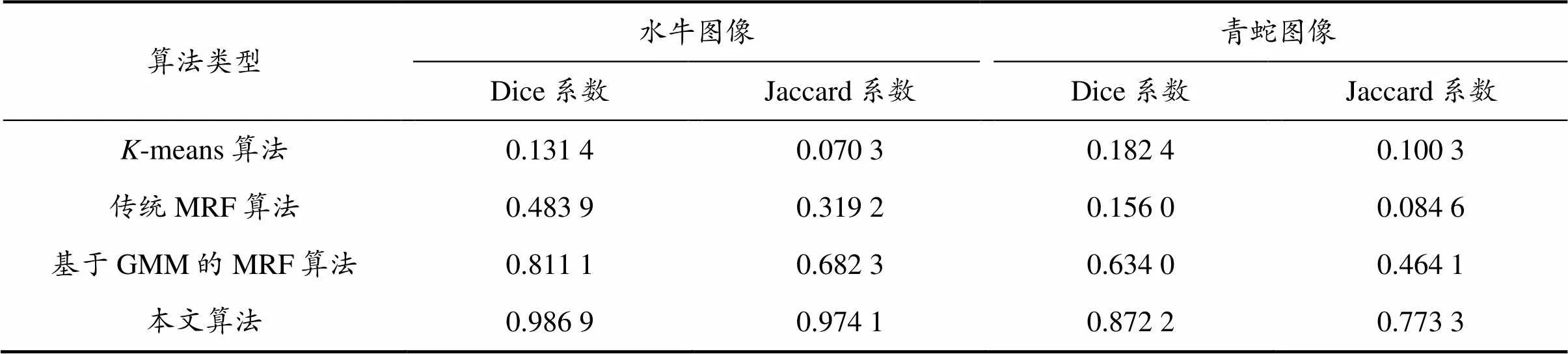
表2　水牛、青蛇图像不同算法的评价结果

［1］陶启放.基于Markov随机场的机器视觉设计及应用［D］.成都：电子科技大学，2018．

［2］刘长齐，邵堃，霍星，等.基于加权质量评价函数的-means图像分割算法［J］.计算机科学，2019，46（S1）：158-160．

［3］Moftah H M，Azar A T， et al . Adaptive-means clustering algorithm for MR breast image segmentation［J］. Neural Computing and Applications， 2014， 24（8）：1917-1928.

［4］Macqueen J. Some methods for classification and analysis of multivariate observations［C］//Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. California： University of California Press， 1967.

［5］彭代强，李家强，林幼权.基于模糊隶属度空间约束的FCM图像分割［J］.计算机科学，2010，37（10）：257-259．

［6］朱瑶.基于马尔科夫随机场模型的图像分割算法研究［D］.哈尔滨：哈尔滨工程大学，2014．

［7］肖然，侯进.基于马尔科夫模型的多分辨率图像分割算法［J］.计算机工程，2012，38（16）：223-232．

［8］徐胜军，韩九强，刘光辉.基于马尔科夫随机场的图像分割方法综述［J］.计算机应用研究，2013，30（9）：2576-2582．

［9］刘磊，石志国，宿浩茹，等.基于高阶马尔科夫随机场的图像分割［J］.计算机研究与发展，2013，50（9）：1933-1941．

［10］ Kumar M P， Torr P， Zisserman A. Solving markov random fields using second order cone programming relaxations ［C］//2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition （CVPR'06）. New York： IEEE Presss， 2006.

［11］ 刘光辉，任庆昌，孟月波，等.自适应先验马尔可夫随机场模型的图像分割算法［J］.西安交通大学学报，2013，47（10）：62-67.

［12］ 徐迪.马尔科夫随机场在图像分割方法中的应用研究［D］.哈尔滨：哈尔滨工业大学，2013．

［13］ 祖成玉.基于邻域统计特征MRF的图像分割算法［D］.大连：大连海事大学，2018．

［14］ Smith G B. Stochastic relaxation， gibbs distributions and the bayesian restoration of images［J］.IEEE Trans. Pattern Anal.1984， 26（9）：721-741．

［15］ Zhang Y， Smith S， Brady M. Hidden markov random field model and segmentation of brain MR images［J］. Proceedings of SPIE-The International Society for Optical Engineering， 2000， 20：45-57.

［16］ 杨俊，李娜，李迟迟，等.基于高斯混合模型和马尔科夫随机场的脑MR图像分割［J］.解剖学研究，2018，40（5）：425-429．

［17］ Melas D，Wilson S. Double markov random fields and bayesian image segmentation［J］. IEEE Trans.on Signal Processing， 2002， 50： 357-365．

［18］ 柴五一，杨丰，袁绍锋，等.用于图像分割的多分类高斯混合模型和基于邻域信息的高斯混合模型［J］.计算机科学，2018，45（11）：272-277．

［19］ Wang Q. Implementation of the hidden markov random field model and its expectation-maximization algorithm［EB/OL］. （2012-12-18）［2020-07-30］. http：//export.arxiv.org/pdf/1207.3510.pdf，

［20］ 标本，梁恺彬，管一弘.高斯马尔科夫随机场的人脑MR图像分割方法［J］.计算机技术与发展，2017，27（7）：180-184．

［21］ 吴倩倩.基于聚类与区域合并的彩色图像分割算法的研究［D］.哈尔滨：哈尔滨工业大学，2017.

［22］ 胡学刚，段瑶，严思奇.基于区域合并的FCM图像分割改进算法［J］.小型微型计算机系统，2018，39（9）：2077-2080．

［23］ Dice L R. Measures of the amount of ecologic association between species［J］. Ecology， 1945， 26（3）： 297-302.

［24］ Jaccard P. The distribution of the flora in the alpine zone［J］. New Phytologist， 1912， 11（2）： 37-50.

An Improved Image Segmentation Algorithm Based on MRF and Region Merging

Wang Guoliang， Ren Yunshuai

（School of Information and Control Engineering，Liaoning Petrochemical University，Fushun Liaoning 113001，China）

The existing image segmentation algorithms based on Markov random field are prone to over segmentation and the segmentation results are not ideal. This paper presents an improved image segmentation algorithm based on Markov random field and region merging. First, the algorithm uses the image segmentation algorithm based on the theory of Markov random field and Gaussian mixture model to get the initial segmentation results; second, the region distance between each region is given by using the adjacent relationship, color relationship and boundary condition of each region; finally, the initial segmentation is performed according to the distance between regions and the change rate of color divergence after region merging. The final image segmentation results are output by region merging. In this paper, Berkeley standard image library is used for experimental simulation, and the Dice and Jaccard coefficients are used as the evaluation index of this paper. The experimental simulation shows that the proposed algorithm has better segmentation effect than the existing algorithm based on MRF theory.

Image segmentation； Markov random field； Gaussian mixture model； Region merging

TP37

A

10.3969/j.issn.1672-6952.2021.04.013

1672-6952（2021）04-0078-07

http：//journal.lnpu.edu.cn

2020-07-30

2020-09-18

国家自然科学基金项目（62073158、61473140）；辽宁省“兴辽人才”支持计划项目（XLYC1807030）；辽宁省“高校创新人才”计划项目（LR2017029）；辽宁省教育厅科研基金项目（L2016024）。

王国良（1981-），男，博士，教授，从事Markov随机过程的建模及应用方面的研究；E-mail：glwang@lnpu.edu.cn。

（编辑 陈 雷）