残差T2控制图中多元自相关过程模型研究
2021-08-15杨茜婷
杨茜婷
(燕山大学 理学院,河北 秦皇岛 066004)
一、引言
自相关过程在各行业领域随处可见,如工业生产、公共医疗保健、畜牧生产体系和分析实验室等。传统控制图要求序列彼此独立,自相关性的存在使得常规控制图监控效果不准确,导致漏报虚报的现象发生。此外,产品功能的多样化使得需要监控的质量不唯一,同时监控多个质量是统计质量控制的必然趋势,因此,从多元自相关序列出发,将自相关过程转换为独立的残差,设计合理的残差控制图具有重要的现实意义。
目前看,国内外学者已对残差控制图进行了大量研究。在国外,Layth和Harry首次提出了残差控制图[1]。Lu和Reynolds对比了残差均值和方差取不同偏移量时在Shewhart、CUSUM、EWMA三种控制图下的异同点[2][3]。对于整合应用控制图,Lin和Adams提议联合使用残差控制图和EWMA控制图[4]。国内对该领域的研究起步较晚,孙静、徐立广和杨穆尔是最先研究该领域的学者。他们在国内首先提出残差控制图,并引进适用于生产过程自相关的调整均值控制图理论[5];对于残差T2控制图,从二元自相关过程发展到多元自相关过程[6][7]。朱慧明和赵锐借助贝叶斯统计质量控制模型获得残差,并用残差控制图进行监控[8]。孙秋霞和高齐圣研究序列相关性对残差控制图性能的影响,发现残差控制图在负相关过程中性能更好[9]。
以上对自相关残差控制图的研究,无论数据呈几阶自相关,学者们大多采用一阶自回归模型拟合数据。对于单变量自相关情形,肖艳和李亚平等人已通过实验对这种做法的合理性进行了验证[10]。本文针对多元自相关过程,通过蒙特卡洛方法对基于残差T2控制图的多元自相关模型进行研究,比较VAR(1)与VAR(p)预测下残差控制图的性能,并分析导致性能差异的原因。
二、拟合模型与方法
由p(p≥2)阶多元自回归模型产出的自相关数据,均可以用一阶VAR(1)和同阶 VAR(p)模型进行拟合,计算数据的真实值与拟合后的预测值之差即得到残差向量,计算得到对应的T2统计量,通过残差T2控制图监控多元自相关过程。
(一)高阶多元自相关拟合模型的构建
1.VAR(p)拟合模型
在多元自相关过程中,VAR(p)模型的表达式为

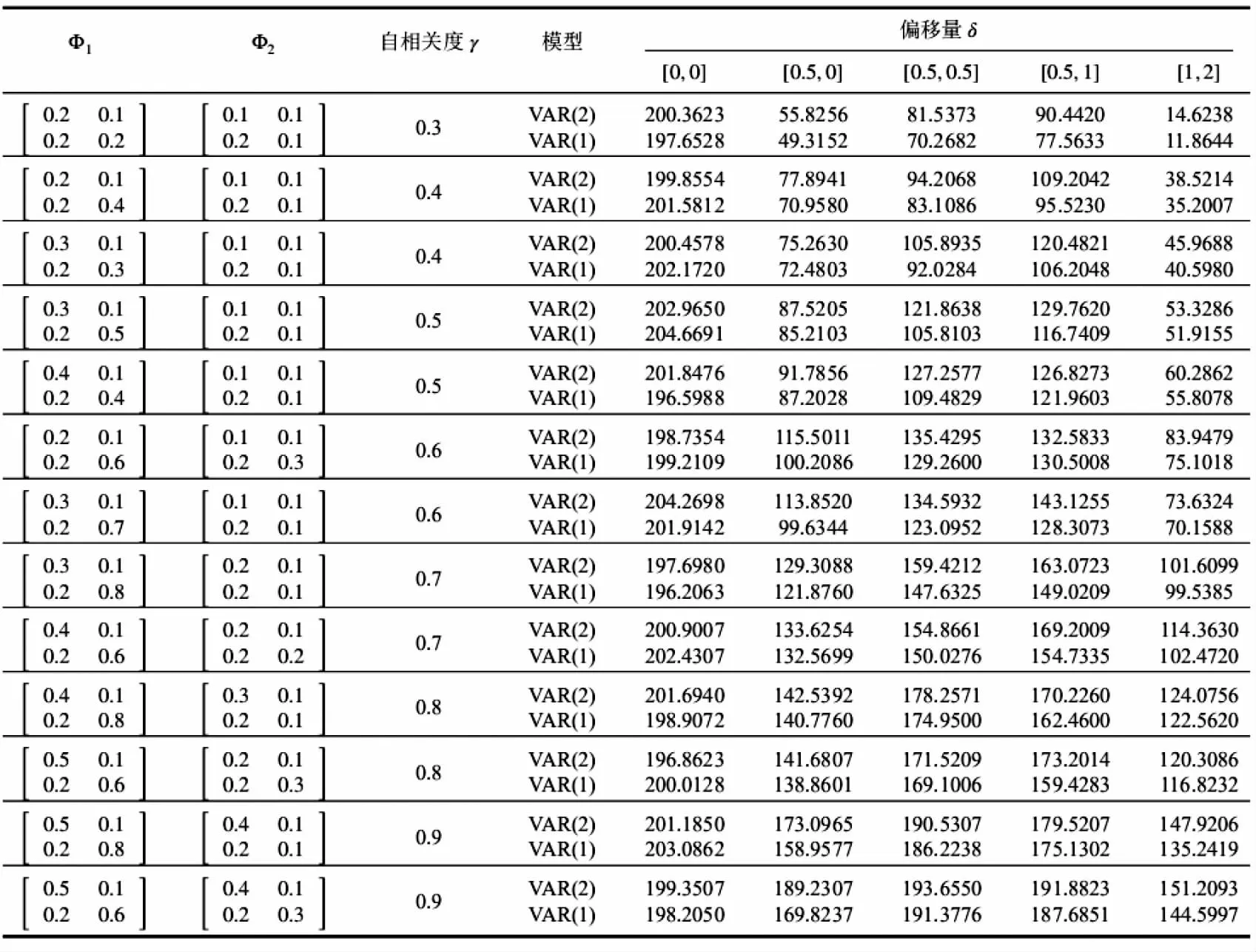
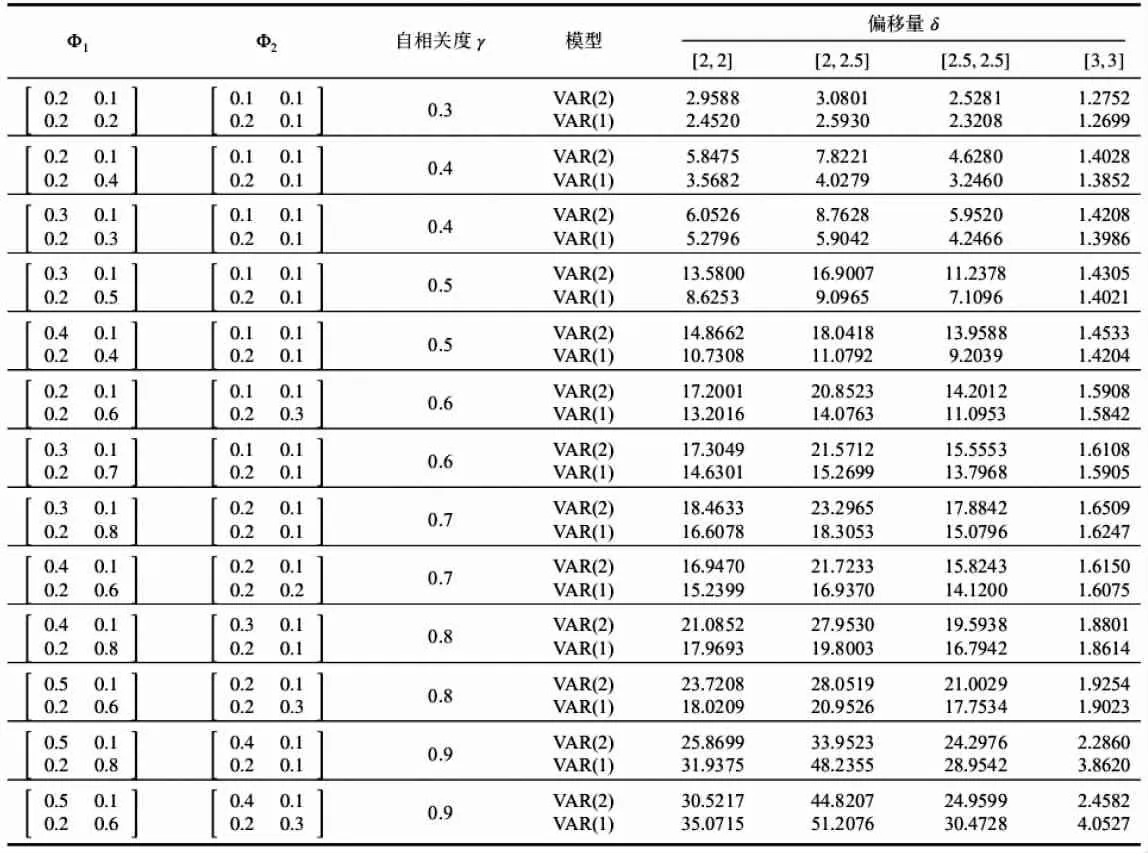
其中μ为受控的过程均值;Φ1,…,Φp为自回归系数矩阵,Φp≠0;εt为误差向量,服从正态分布,E(ε)t=0,cov(εt,ε)t=∑,∑为一个常值协方差矩阵,对于E(εtεTt+)k当k=0时等于∑,k≠0时等于0;E(Xsε)t=0,s 2.VAR(1)拟合模型 在多元自相关过程中,VAR(1)模型的表达式为: 监控残差T2统计量的控制图即为残差T2控制图。残差T2控制图的下控制限LCL=0,上控制限取F分布控制限: 设残差T2控制图失控的概率为P,则ARL与多元自相关过程中的偏移量δ满足如下关系: 这里定义的残差统计量服从卡方分布,代入(7)式可直接计算ARL作为比较残差T2控制图性能的依据。 为不失一般性,设多变量自相关过程的维数为2,规定质量特性的受控均值 μ0=(0,0)T,则符合条件的二维VAR(p)模型满足: 下面定义VAR模型的自相关度γ,以p=2为例,计算公式如下: 为了直观比较 VAR(1)与同阶 VAR(p)(p≥2)预测下的残差T2控制图的性能,并验证结论的普适性,取p=2,3进行仿真实验。下面以二阶自相关数据为例介绍随机模拟过程。 对于定义的模型(8),取p=2,并给定符合要求的Φ1和Φ2,通过蒙特卡洛方法生成一组二阶自相关数据。然后,运用最小二乘法估计得到二阶自相关数据的VAR(1)模型和VAR(2)模型预测值。设犯第一类错误的概率α=0.005,则受控状态下预期的平均运行链长为200。以delta为依据,选取δ并代入式(7)中,分别计算在模型VAR(1)和模型VAR(2)预测下的残差序列在残差T2控制图中受控和失控的ARL。具体的取值方案如下: 由于VAR模型的自相关度只由Φ1和Φ2的对角元素决定,所以可保证非对角元素不变,其中c12=0.1,c21=0.2,通过调整其对角元素改变求和后对角元素的值,进一步改变模型的自相关度。以delta值取2.5作为偏移量大小的分界点,将δ的取值分为如下三种情形:受控时取[0,0];较小偏移时取[0.5,0],[0.5,0.5],[0.5,1],[1,2];较大偏移时取 [2,2],[2,2.5],[2.5,2.5],[3,3]。比较两种模型预测下的平均链长在不同偏移程度delta下的优劣。实验结果见表1、表2。 表1 VAR(2)和 VAR(1)预测下残差 T2控制图的 ARL(delta≤2.5) 表2 VAR(2)和 VAR(1)预测下残差 T2控制图的 ARL(delta>2.5) 肖艳和李亚平等人发现用VAR(1)模型拟合的残差序列具有负自相关性[10]。所以对于多元自相关过程,残差向量可以用如下多元线性模型进行拟合,满足: 其中k为大于0的常数,b为常数向量,ε为误差项随机向量。所以对于(t-1)时刻的T2统计量T2(t-1)=e(t-1)T∑(0)-1e(t-1),将式(10)代入,转化后得到: 其中k、b为常数,ε是误差项随机变量。VAR(1)模型拟合的残差T2统计量序列满足正自相关关系,使残差T2控制图性能更好。 此外,肖艳和李亚平等人通过实验发现在自相关程度下降时,一阶自回归模型预测下的残差序列负自相关的程度会减弱,导致公式(10)中的 k→0,从而式(11)中的k2→0。因此在多变量自相关过程中,自相关程度的减弱会导致VAR(1)拟合下的残差T2统计量的正自相关性减弱,使残差T2控制图探测异常变得灵敏。 对于三阶多元自相关数据,同样用上述随机模拟方法,得出的结论一致,即VAR(1)下的残差T2控制图优于VAR(3)。同时,影响残差T2控制图性能的因素也与二阶的情形相同。验证了上述结论的普适性。 本文主要对基于残差T2控制图的多元自相关过程模型进行研究。通过随机模拟实验,对比分析两种模型下的ARL,发现通过VAR(1)预测的残差T2控制图的性能优于VAR(p)拟合模型,这一发现可以使对残差T2控制图的后续研究减少定阶过程,以节约定阶所需的时间和成本。这一发现也与肖艳、李亚平等人对单变量情形的研究结论基本一致。◆

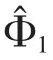

(二)残差T2控制图


三、基于模型阶数的残差T2控制图性能对比
(一)前期准备
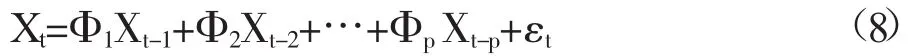
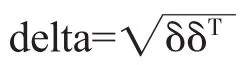


(二)随机模拟生成ARL
(三)残差T2控制图性能分析
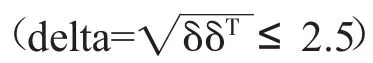


四、结语
