振动式土壤切削系统的振动频率范围研究*
2021-08-13张印郭志军田晨乐庞靖张盼港邱毅清
张印,郭志军,田晨乐,庞靖,张盼港,邱毅清
(1. 河南科技大学车辆与交通工程学院,河南洛阳,471003; 2. 河南科技大学农业装备工程学院,河南洛阳,471003)
0 引言
采用振动方式在特定工况下可以有效减小土壤切削阻力[1-2],目前主要有强迫振动[3-4]和自激振动[5-6]两种形式。强迫振动主要通过对土壤切削机具加装额外激振装置来实现[7],在特定频率、振幅、土壤条件和工作方式下可取得良好减阻效果[8-10]。这种方式可以起到明显的减阻效果,但是机具和土壤参数一旦不协调,极易出现系统总功耗增加的情况[11-12]。自激振动是在非均匀土壤阻力作用下,利用切削部件自身弹性,使切削部件—土壤相互作用系统产生振动[13],起到迅速松碎土壤和减阻效果[14-15]。自激振动应用较成熟的有弹齿和切削工具铰支再附加弹簧[16]两种,也都存在机具振动参数与复杂土壤条件相互适应问题[17]。无论是哪种振动形式,拓宽机具本身振动参数与土壤固有振动参数彼此之间的匹配和适应能力成为亟待解决的问题。
在频率、阻尼比和振幅等振动参数中,频率参数是首要因素,它决定了振动式土壤切削的性质和减阻效果。查阅大量振动式土壤切削机具通过土槽[18-19]或田间耕作[20-21]测试研究成果,发现已采用的机具振荡频率分布范围非常广,从2 Hz到50 Hz都有采用,并声称都取得了较好的减振效果。这对形成相关振动式土壤切削机具参数设计指导性意见就显得比较困难。
振动式土壤切削机具工作过程中,机具与被切削土壤之间振动参数的合理匹配是有效减阻的关键。工程结构在发生共振现象时极易破坏。故本文引入共振理论来探索振动式土壤切削机具振动参数,特别是振动频率的选取原则。即当机具冲击振荡频率与土壤固有振动频率比较接近而使被切削土壤发生共振现象时,具有散体材料特征的土壤更易破碎,从而为获得极低土壤切削阻力创造物理条件。
在测得室内土槽土壤固有振动参数基础上,以单自由度土壤振动切削模型共振效应分析为基础,分别使用经验值、半功率带宽、振幅放大因子和正态分布等四种方法对土壤第一阶固有振动共振频带宽度和振动能量占比进行计算和分析,以期为强迫和自激等各类振动式土壤切削机具振动参数设计,特别是振动频率选择,以及相关产品开发提供参考。
1 单自由度土壤振动切削模型
在图1(a)所示切削部件—土壤二维切削模型中,取切削前进方向,即水平+x方向为例,可建立图1(b)所示土壤单自由度振动模型。

(a) 实际模型
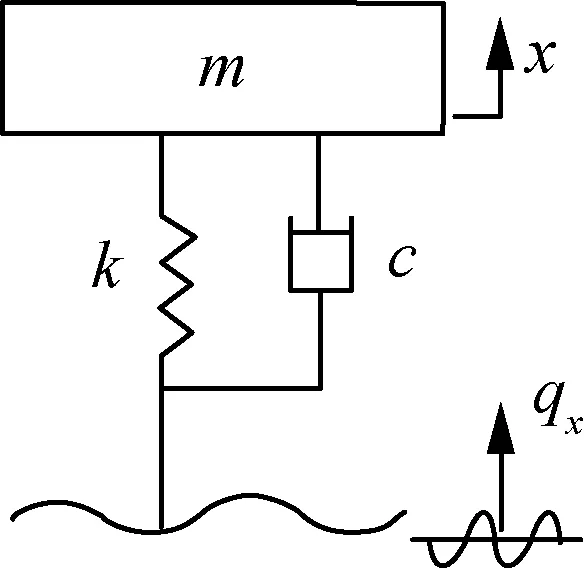
(b) 简化模型图1 单自由度土壤振动切削模型Fig. 1 Single freedom soil vibration cutting model
根据牛顿第二定律,可得图1(b)系统运动微分方程
(1)
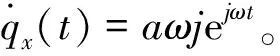
代入式(1)有
B(-mω2+ωjc+k)=a(jωc+k)
(2)
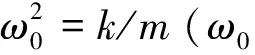
(3)
与放大因子形式相同的幅频特性方程[23]
(4)
相频特性方程[22]
(5)
以阻尼比ζ=0.1为例,此系统的幅频和相频特性曲线分别如图2(a)和图2(b)所示。当触土部件冲击频率等于土壤固有振动频率,即图2中系统频率比λ接近于1时,系统幅频特性取得极大值点,即系统共振点。或者说,当频率比λ接近于1时,触土曲面前方土壤产生共振现象,土壤容易破碎,从而可能获得较低土壤切削阻力。
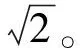
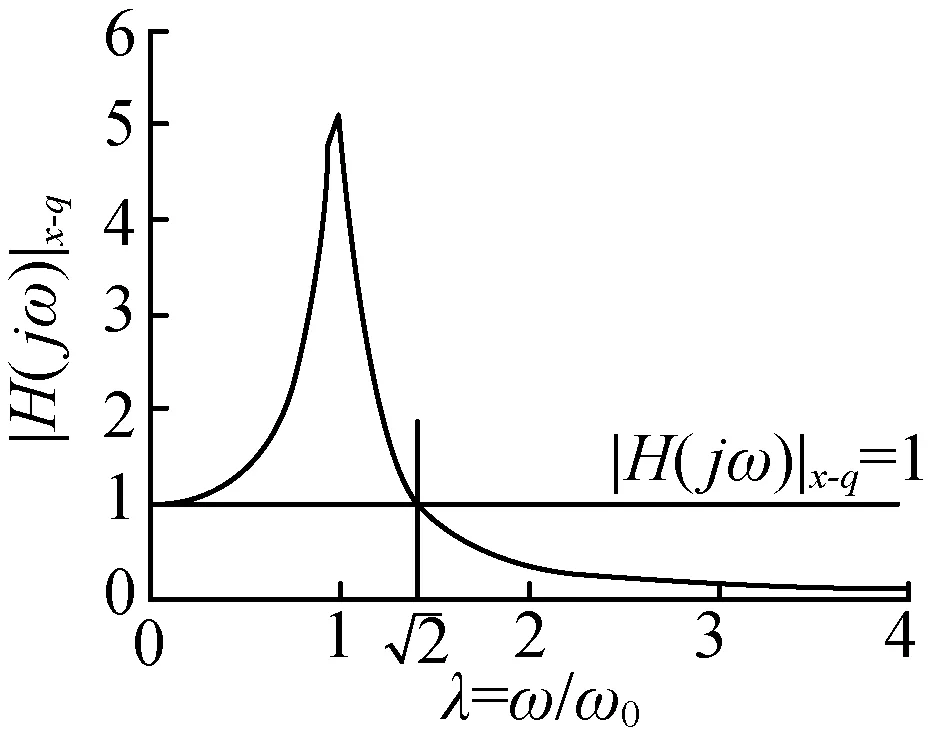
(a) 幅频特性
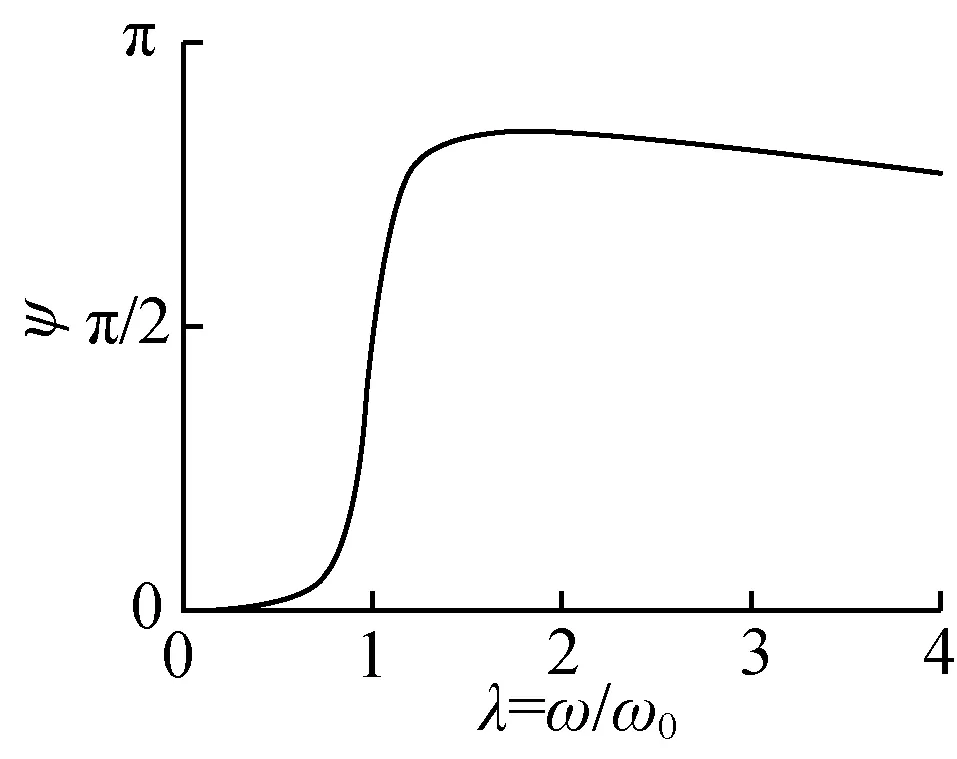
(b) 相频特性图2 单质量系统幅频和相频特性Fig. 2 Amplitude-frequency and phase-frequencycharacteristics of single-mass system model
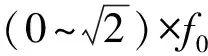
2 土壤固有振动参数测试
测试了室内土槽土壤的固有振动参数。图3所示土槽内轮廓尺寸为1.5 m×0.8 m×0.5 m。经全面松碎、打匀、刮平和压实后的有效土体尺寸为1.5 m×0.8 m×0.35 m,体积密度1 394.38 kg/m3、烘干法土壤含水量均值12.45%。

图3 试验现场Fig. 3 Test site1. 加速度传感器及测点布置 2.土槽 3.土壤4.DH5902数据采集分析系统 5.DHMA模态分析系统 6.激振锤
室内土槽设计的目的是为了完成各种铲刀切土试验。为了说明问题,结合铲刀切削工况,对土槽土壤依照右手螺旋定则建立三维坐标系。图3所示土槽土体上表面纵向中心线与右端面钢板交点为坐标原点,该平面为xOy平面。图4给出了该土体上表面俯视图,铲刀切削前进方向为+x方向(图3土槽指向左侧),垂直于土体表面向上为+z方向,左侧为+y方向。
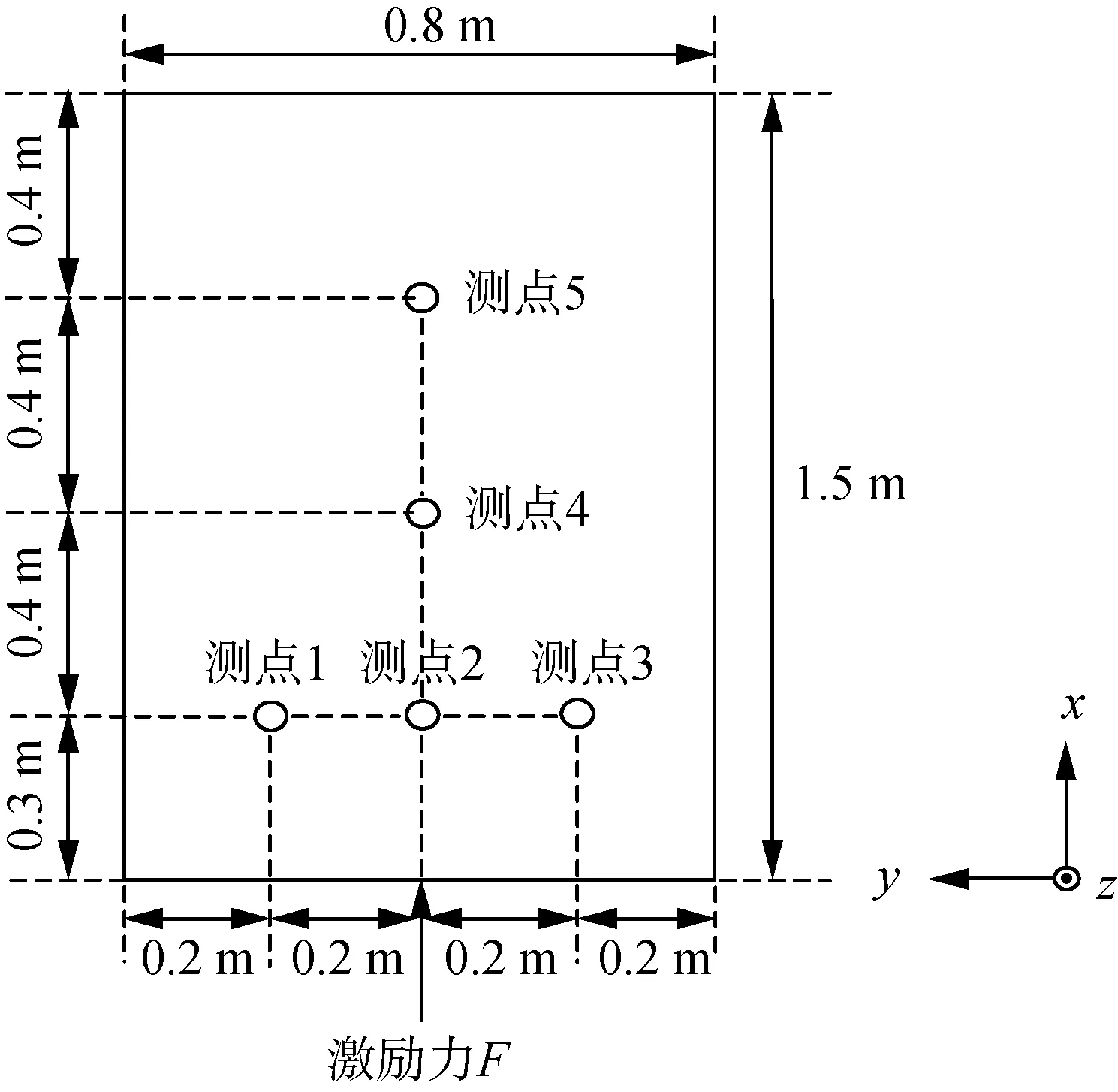
图4 测点与激励点位置示意图Fig. 4 Schematic diagram of response points andexcitation point position
土槽土壤固有振动参数可通过频率响应函数或自由衰减振动测试得到。具体采用锤击式脉冲激励—自由衰减振动法完成了相关土壤振动参数测试工作。激振锤的激振位置位于图3土槽右端面。该点距离土壤上表面0.1 m,激振方向为+x方向,具体激励点坐标位置为(0,0,-0.1),参见图4。选取这个激振点位置和方向是综合考虑了土槽试验时模型铲刀工作深度和前进方向。土壤振动响应通过压电式加速度传感器测得。试验时,将各传感器埋入土壤表层,传感器自身高度为16 mm,其上表面与土壤表面齐平。传感器布置位置主要考虑了铲刀尺寸、工作方向以及信号响应强弱[24]。全部试验的测点分布是由78个100 mm×100 mm 的网格组成,共计98个测点,经测试发现沿纵向中心线即切削前进方向的响应依次减弱,靠近图3土槽右端的测点响应较强。限于篇幅选取其中代表性的五个测点进行阐述,见图3和图4。1~5号各测点传感器在x-y平面的具体位置坐标为(0.3,0.2)、(0.3,0)、(0.3,-0.2)、(0.7,0)和(1.1,0)。各加速度传感器对振动信号接收方向均为x方向。
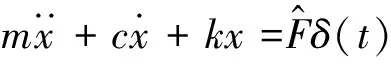
(6)
式中:δ(t)——单位脉冲函数。
试验时由加速度传感器获得的振动信号输入东华测试DH5902数据采集分析仪,经动态分析软件获得各振动信号的时间历程、自功率谱、相干函数图等。信号传输路径如图5,仪器设备连接照片见图3。
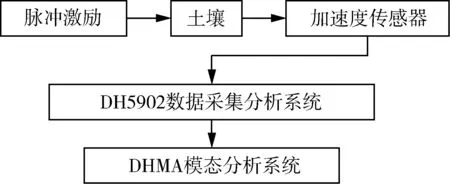
图5 信号传输路径Fig. 5 Signal transmission path
经多次重复试验,试验结果比较接近。五个测点加速度信号的代表性时间历程、自功率谱、相干函数曲线如图6~图10所示。
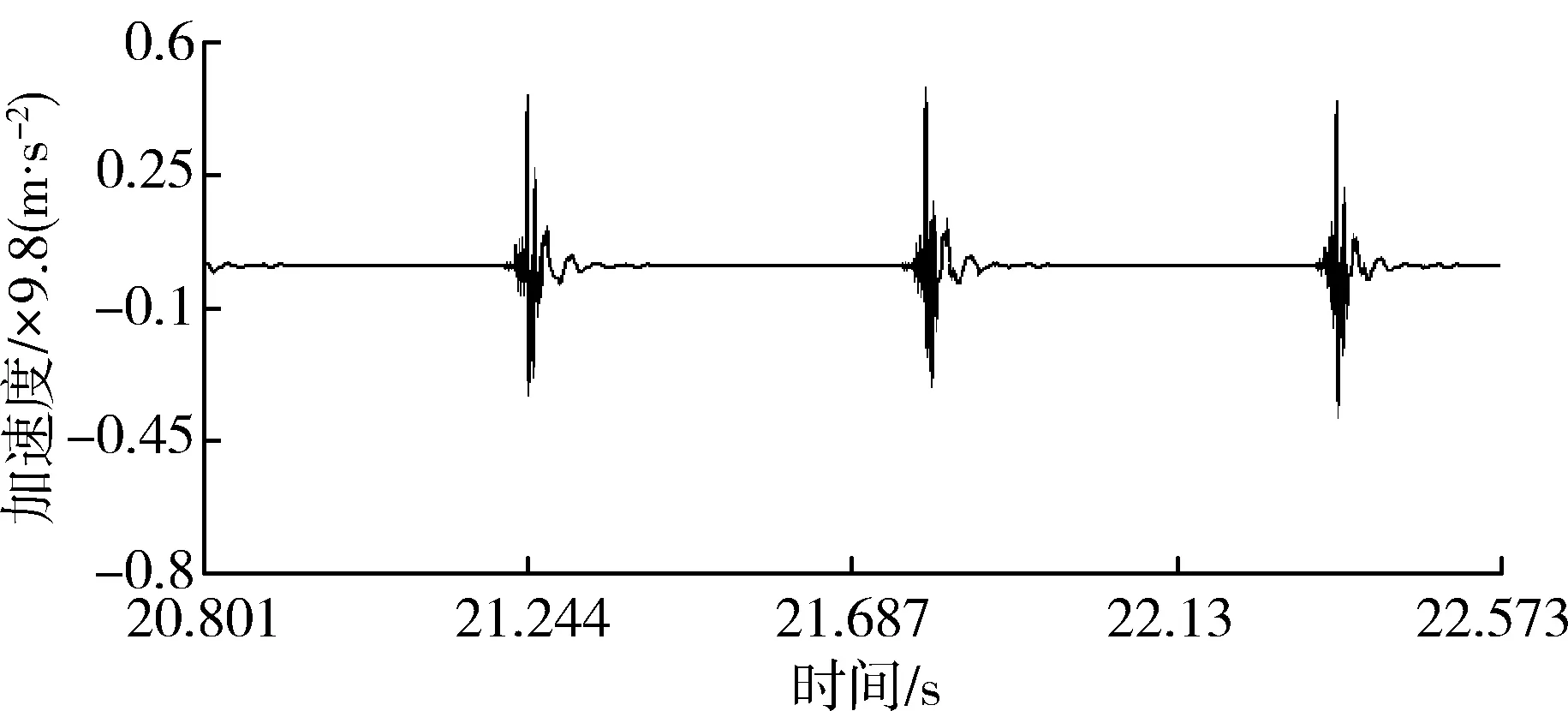
(a) 加速度信号时域图
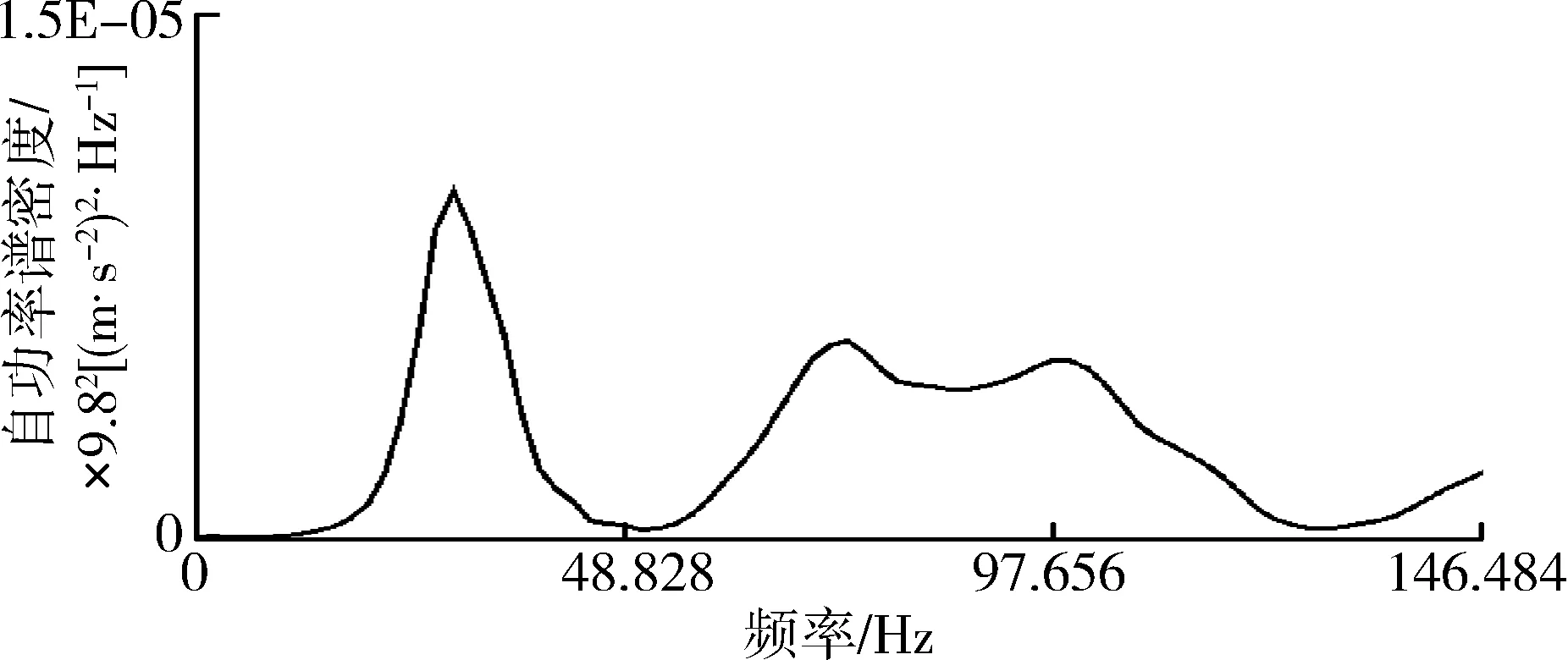
(b) 自功率谱

(c) 相干函数图6 测点1测试结果Fig. 6 Test results of point 1
本次试验五个测点x方向第一阶固有振动频率依次为29.297 Hz、29.297 Hz、27.344 Hz、31.25 Hz、31.25 Hz,均值为29.688 Hz,标准差为1.461。其中响应测点1、2、3距离激励位置较近,因此其振幅信号也较清晰,这三个点第一阶振动频率处对应相干函数值分别为0.981、0.983、0.964,振动特征明显。而测点4和测点5距离激励点的位置越来越远,虽然30 Hz振动频率附近相干函数值也较高,但测得的振幅信号越来越弱。这与实际土壤振动衰减情况是相符合的。因此,仅选取测点1、2、3具有较强振动信号的测试结果展开深入研究。因各测点的第二阶振动频率处振动幅度相对较弱,相干函数值较小,频率范围约为70~110 Hz,峰值点不够清晰,也不易被通常比较低的土壤切削速度激发,故仅对第一阶振动频率作进一步的计算和分析。
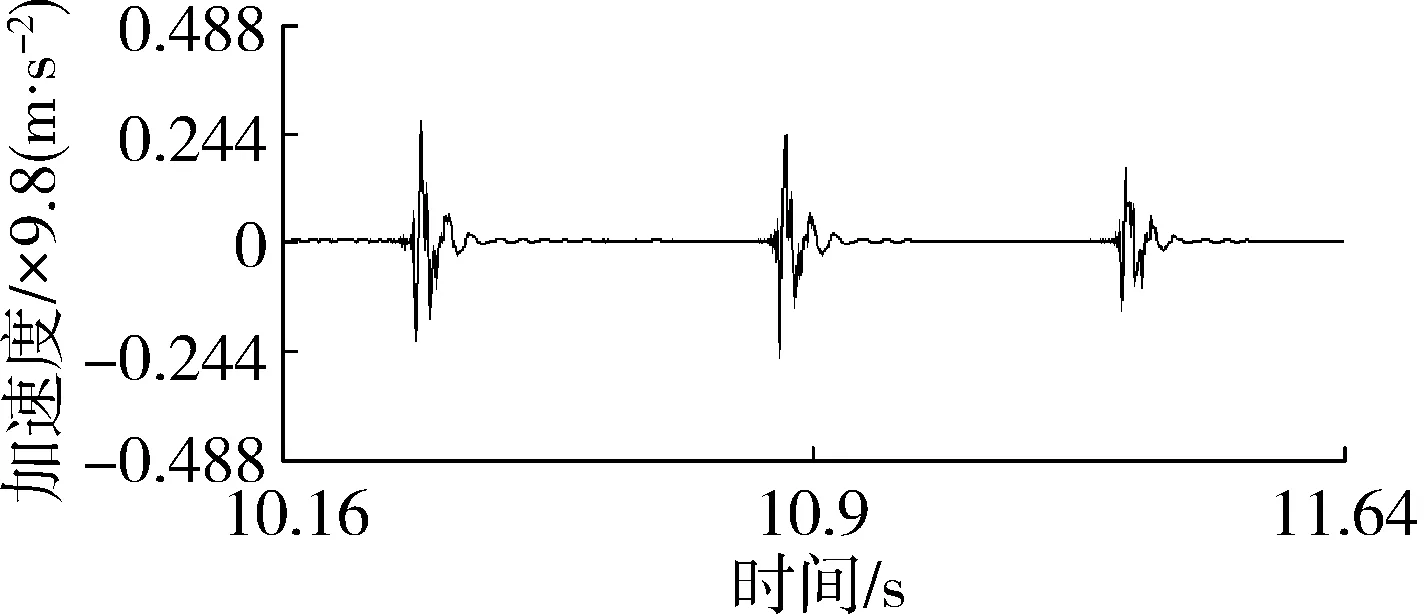
(a) 加速度信号时域图
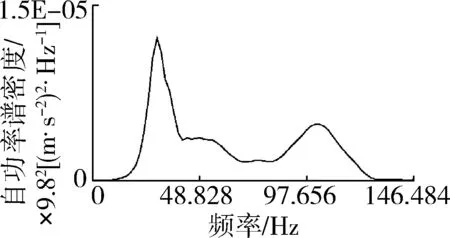
(b) 自功率谱
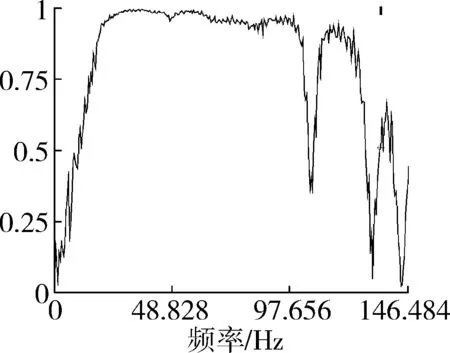
(c) 相干函数图7 测点2测试结果Fig. 7 Test results of point 2
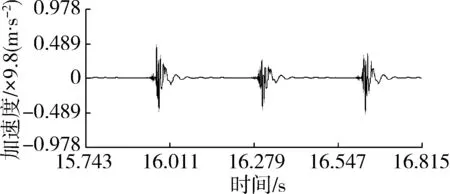
(a) 加速度信号时域图
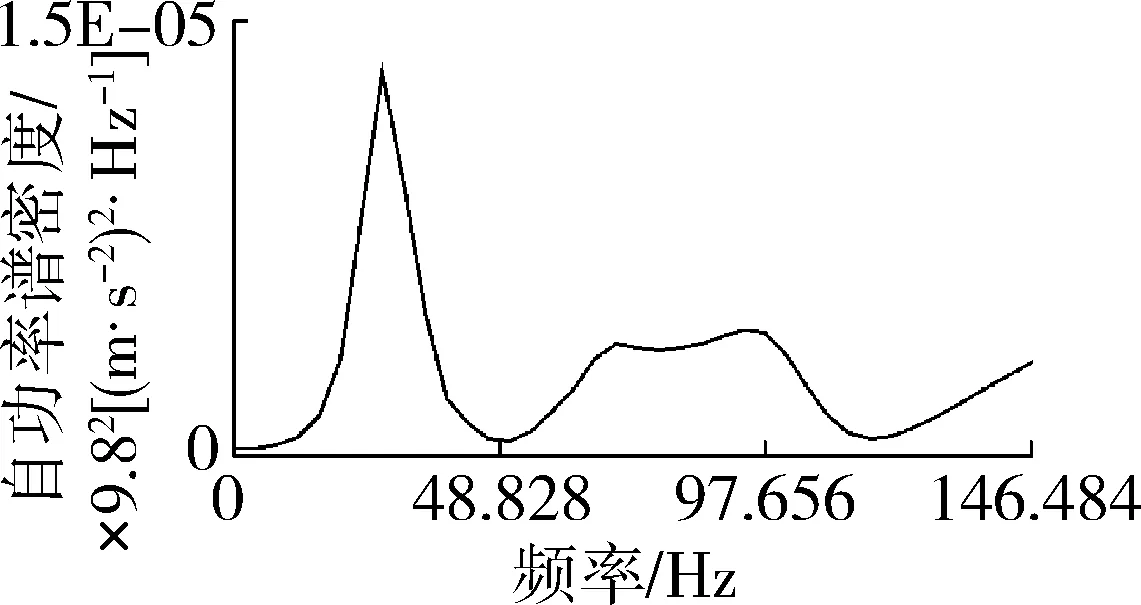
(b) 自功率谱
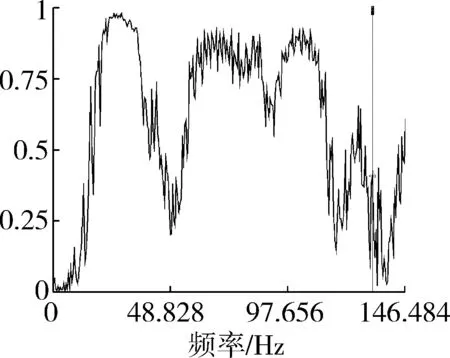
(c) 相干函数图8 测点3测试结果Fig. 8 Test results of point 3
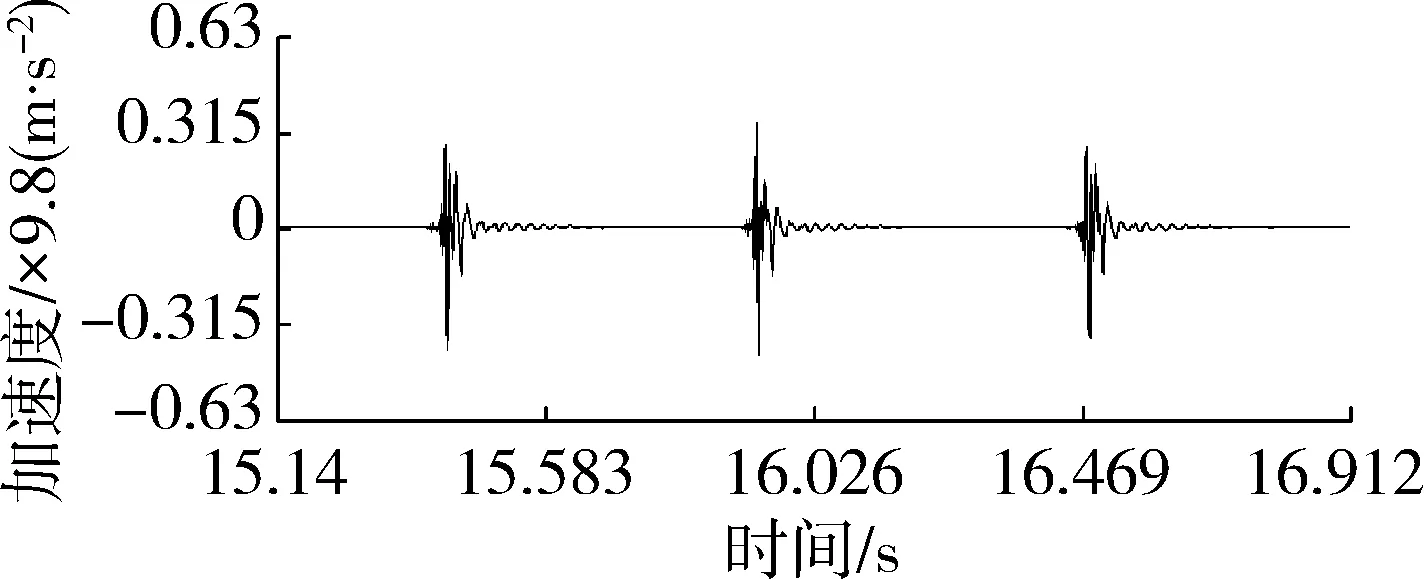
(a) 加速度信号时域图

(b) 自功率谱
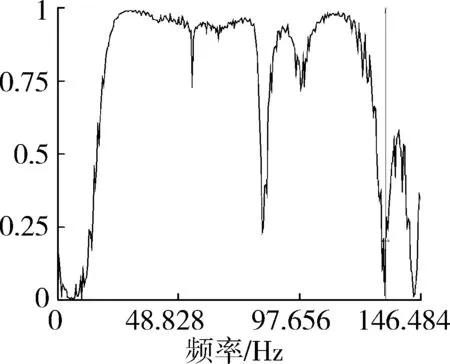
(c) 相干函数图9 测点4测试结果Fig. 9 Test results of point 4
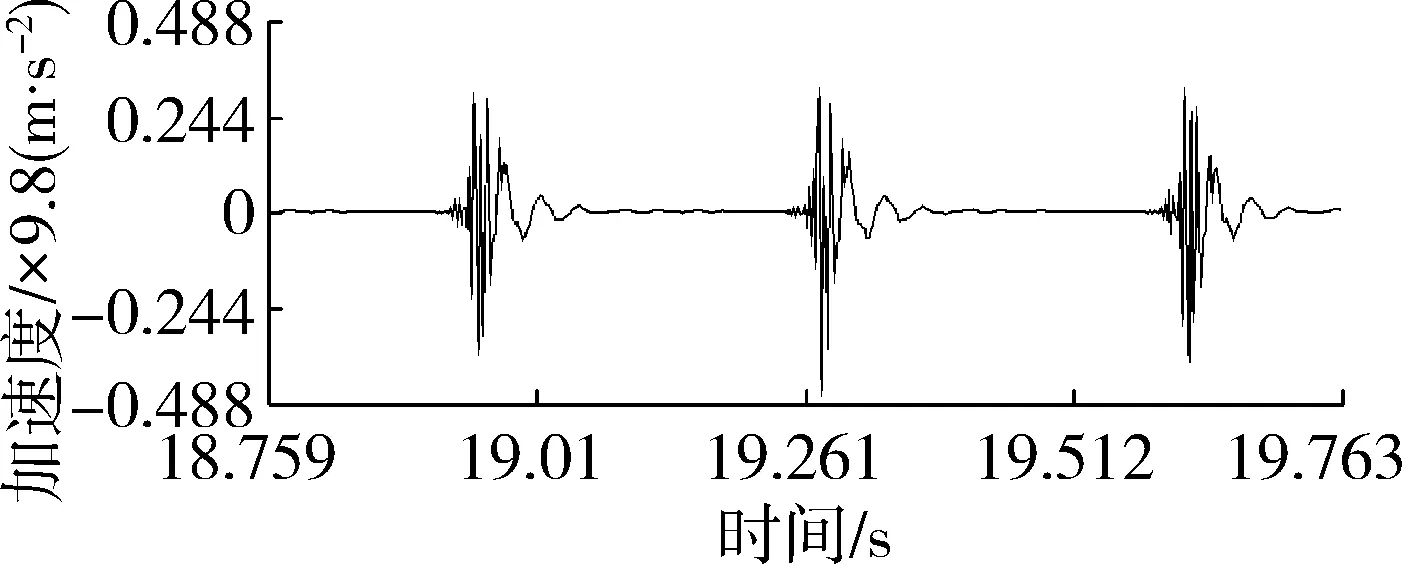
(a) 加速度信号时域图
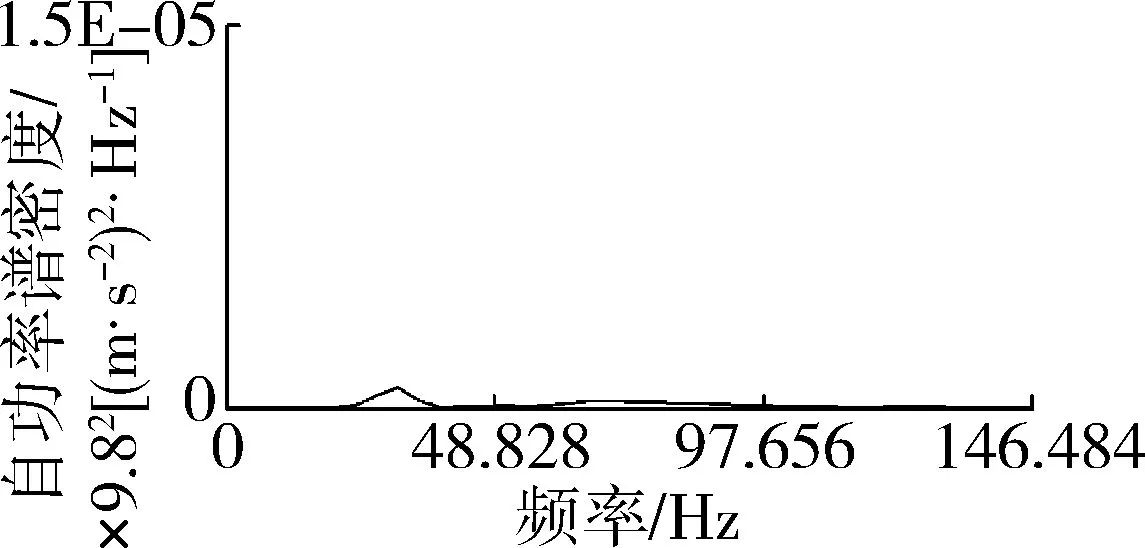
(b) 自功率谱
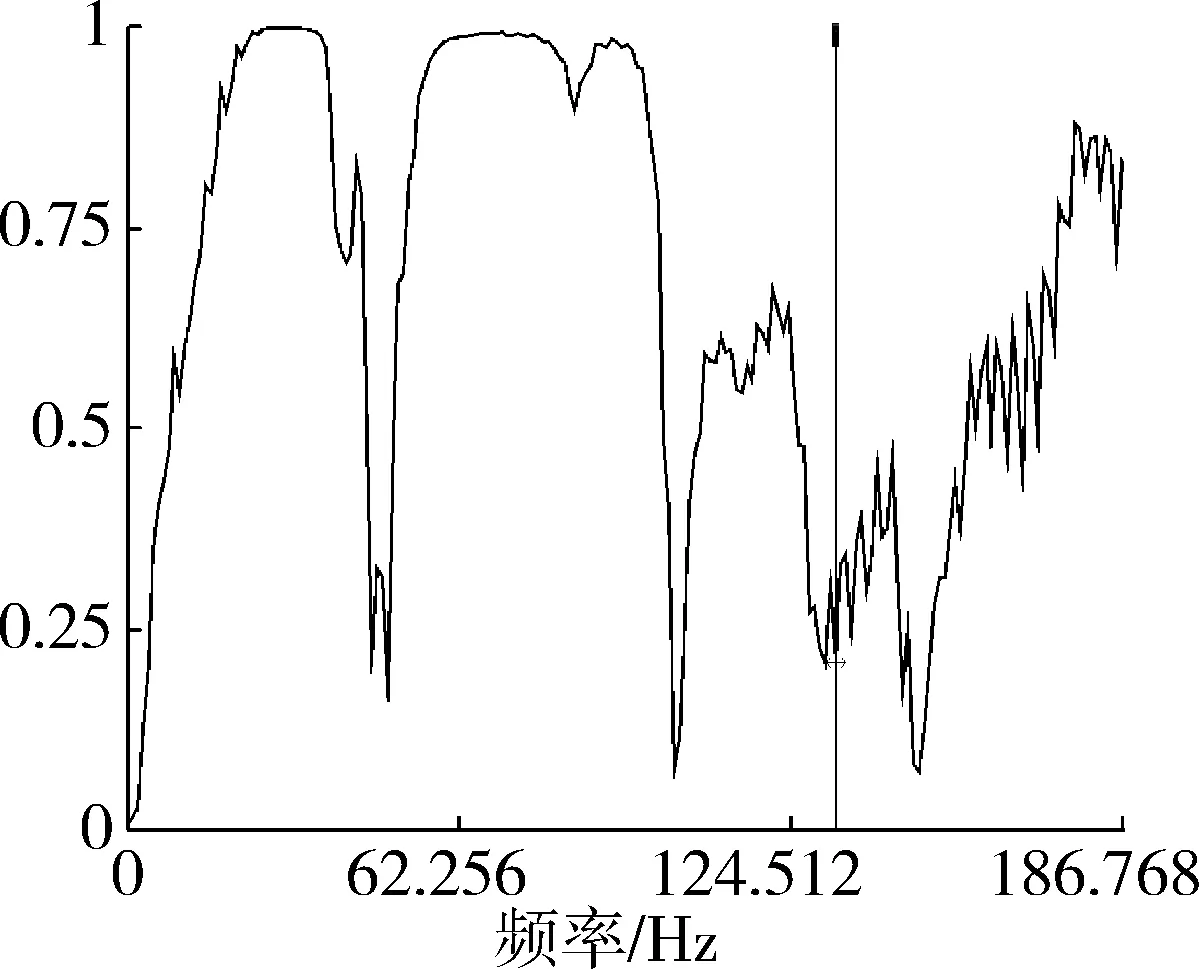
(c) 相干函数图10 测点5测试结果Fig. 10 Test results of point 5
3 土壤共振区宽度与共振能量
为使切削机具工作时产生较好的土壤振动切削减阻效果,一方面,当土壤参数或固有振动频率固定,需要确定切削工具的振荡频率选择或变化范围;另一方面,当机具振动频率固定,需要确定土壤自身参数或固有振动频率宽度的允许变化范围。解决这两个问题的前提是需要探究土壤这种特殊材料的共振区宽度,此处用经验值、半功率带宽、振幅放大因子和正态分布等四种方法展开分析。
功率谱曲线所覆盖的面积在数值上与系统总功率(能量)成正比,故将其积分面积视为振动过程中能量消耗。对于图6(b)所示测点1的自功率谱曲线第一阶共振点附近各坐标点Matlab软件进行曲线拟合,见图11。图中黑色散点为扫描所得图像的散点图,细实线为拟合曲线。
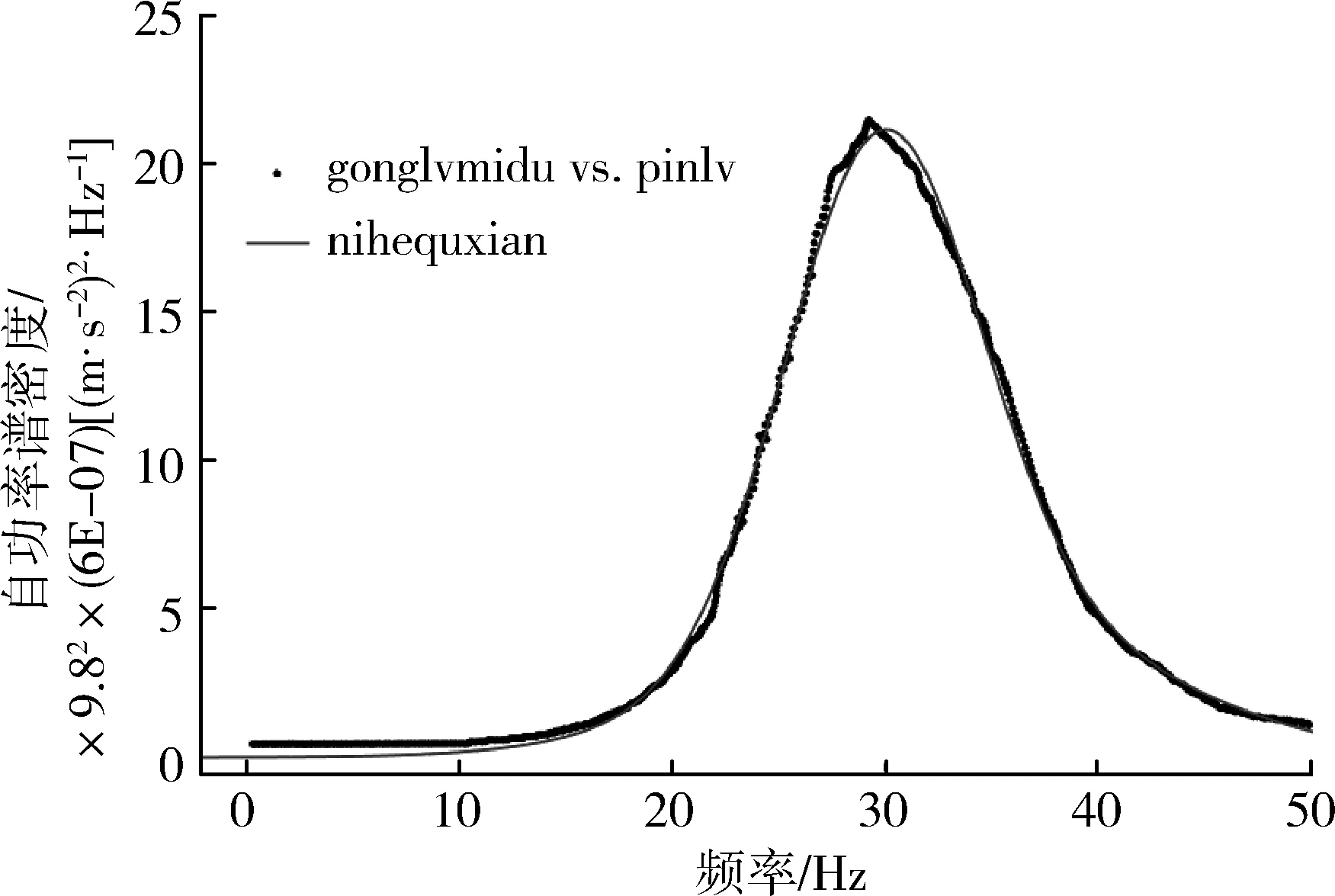
图11 测点1第一阶振动曲线拟合结果Fig. 11 First order vibration curve fitting result ofmeasurement point 1
由高斯逼近方法得到的拟合曲线
(7)

3.1 经验法
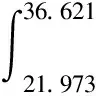
3.2 半功率带宽法
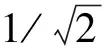
另外,振动系统的阻尼比可由半功率点的频率差与2倍固有频率的比值近似得到[28]
ζ=(f2-f1)/2f0
(8)
利用图6(b)、图7(b)和图8(b)三个测点的自功率谱第一阶振动频率处的数据可计算三个测点的第一阶固有振动阻尼比分别为0.138、0.137、0.152,均值为0.142,均方差为0.006 8。
3.3 振幅放大因子法


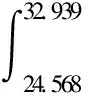
3.4 正态分布法
因正态分布曲线形状与图11中曲线形状有相似之处,为探求共振区范围,故引入正态分布概念对共振区宽度和振动能量进行计算研究。在正态分布中,随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布,其概率密度函数如式(9),记作X~N(μ,σ2)。
(9)
为了使正态分布曲线与图11形状相近,将频率作为样本值,测得的自功率谱密度值作为频次,经计算,当μ=f0=29.297 Hz时,可得σ=7.768。
常用的正态分布区间有1σ、2σ、3σ,分别占总面积68.26%、95.44%、99.74%。参考此区间选择方法,在土壤固有频率f0=29.297 Hz左右加减1σ、2σ、3σ来选择共振频率范围。由此计算出测点1第一阶固有振动共振区频率范围和共振能量占比如下。
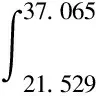
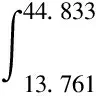
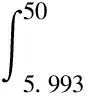
测点2、3第一阶固有振动频率处共振区宽度和共振能量计算过程与测点1一致,限于篇幅,将此略去,结果见图12(b)、图12(c)和表1。
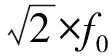
放大因子等于3和半功率带宽法较接近,相应共振区内土壤振动对于机具振动输入的放大超过3倍。虽然放大倍数大,但共振区振动能量占比较低。这种共振区划分对金属等成分均匀且弹塑性较强材料的共振分析较适合,而对土壤这种成分不均匀、且散体特征明显的材料来说显得不是特别必要。虽然放大倍数偏大,有利于碎土,但存在共振区过窄难以适应复杂多变的土壤条件的不足。放大因子等于2(0.717×f0~1.207×f0)、正态分布1σ(0.735×f0~1.265×f0)以及经验法(0.75×f0~1.25×f0)结果比较接近,这三种方法确定的共振区将振动输入信号的幅值放大约超过2倍,共振区所占振动能量约为75%,宽度比较适中。因此这三种方法确定的共振区,对于大部分工程振动的共振分析和设计是合适的。而对于振动式土壤切削机具设计而言,仍可拓展更宽的共振区间以增加对复杂多变土壤条件的适应能力。

(a) 测点1

(b) 测点2

(c) 测点3图12 四种方法计算的共振频率范围Fig. 12 Resonant frequencies range calculated by the four methods
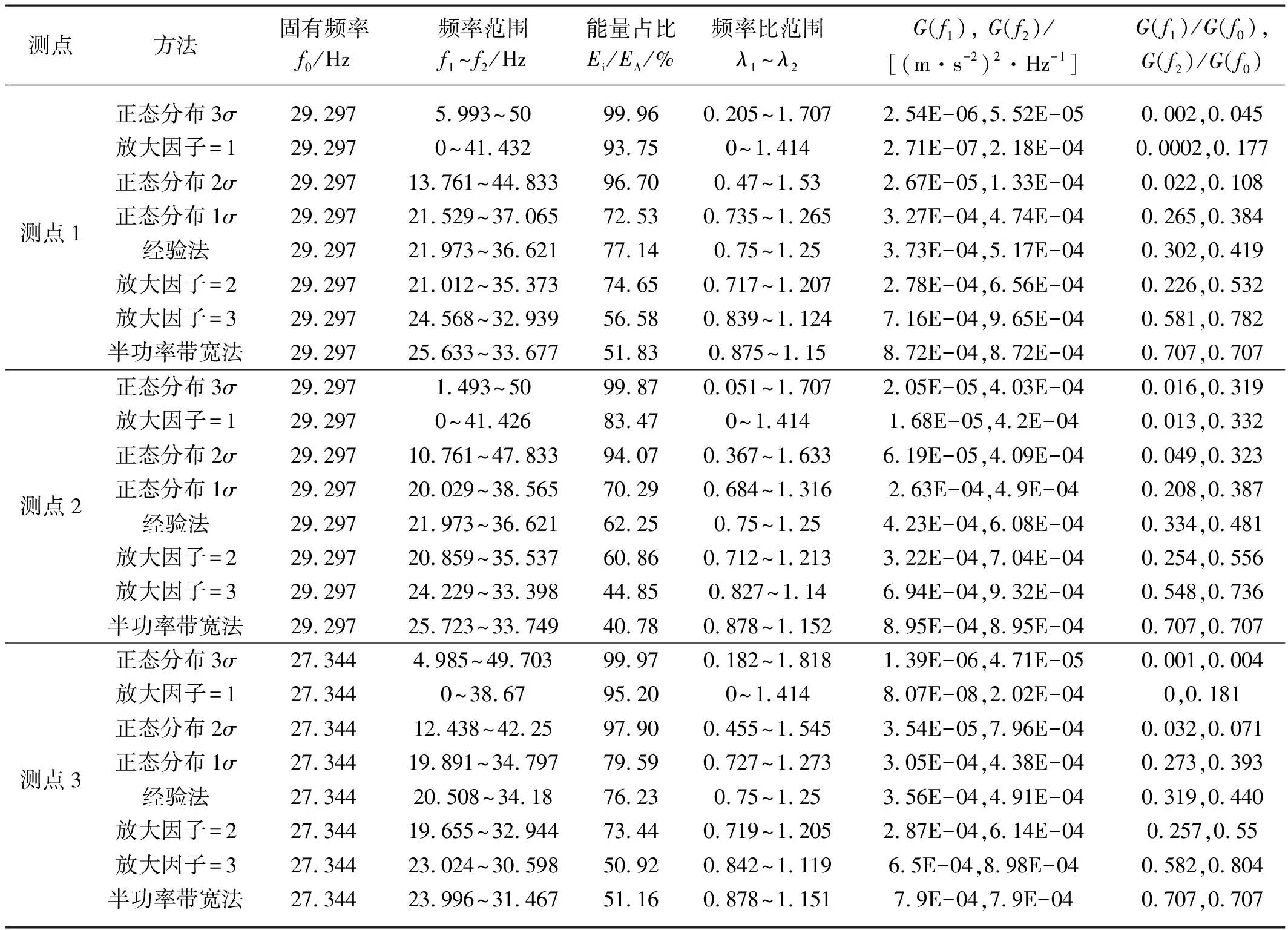
表1 各测点共振区振动参数Tab. 1 Vibration parameters of the resonance zone of each measuring point
4 结论
1) 对室内土槽土壤第一阶固有振动频率测试结果为27.344~31.25 Hz,均值29.688 Hz,标准差1.461。
2) 由半功率带宽法求得室内土槽土壤第一阶振动系统阻尼比范围为0.137~0.152,均值为0.142,标准差为0.006 8。
3) 可采用经验法、放大因子等于2和正态分布1σ所确定的共振区间作为机具振荡频率或系统激励频率的选择范围(约为0.75f0~1.25f0)。这三种方法的结果比较接近,振动参数的大小比较适中。对于土壤类非均匀且散体特征明显的材料振动参数设计而言,仍偏严,对于复杂多变的土壤条件适应能力有限。
4) 采用振幅放大因子等于1确定土壤共振区(0~1.414f0)来设计系统激振频率,在较宽频带范围内可保障系统输入土壤的振动能量不衰减,但某些频率处的振动切削减阻效果可能略弱。
5) 推荐用正态分布2σ(下限频率0.470f0)或者正态分布3σ(下限频率0.205f0)来确定土壤共振区或振动式土壤切削机具的振荡下限频率范围,从理论上即可保证一定的土壤振动强度,又可对复杂多变的土壤条件具有较强适应能力。但这种方法需保证上限截止频率不得超过1.414f0,或可靠起见,依照正态分布1σ上限频率1.265f0截止。
