基于持续同调性的人脑认知过程 格式塔模式识别拓扑分析

刘再生，倪霏，李荣鹏，张宏纲，刘畅，张解放，谢松云

（1. 浙江大学信息与电子工程学院，浙江 杭州 310027； 2. 浙江传媒学院，浙江 杭州 310018；3. 西北工业大学，陕西 西安 710129）

1 引言

6G通信技术的发展带来大带宽、超高速、超低时延的通信性能革新是可以预见的。信息通信技术和神经科学的融合发展预示了脑对脑无线通信（brain-to-brain wireless communication，B2BC）的可能性与巨大潜力。B2BC要实现的技术过程是从发送者大脑把神经信号中提取、数字化，然后传递给接收方大脑[1]。B2BC技术的实现需要高数据速率、低时延和可靠通信的支持，而这正是6G技术可以提供的。B2BC实现神经信号的提取是通过脑电图（electroencephalogram，EEG）的采集，EEG信号最常见的典型分析方法是对原始的时域EEG信号进行滤波、去除伪迹、事件相关电位（event-related potential，ERP）分析以及观察2D或3D脑域活动热图等方式观察其表现出来的特征。对于B2BC而言，复杂的、动态的多路时域EEG信号并不是信息传输的理想载体，在传输与认知过程相关的EEG信号时，每个电极的信号都是至关重要的，但每个电极信号的轻微失真都会导致传输信息的整体偏差。因此B2BC的神经信号数字化过程需要一种可靠的、可以整合多路信号整体特征并且保留局部特征的“编码”方式来数字化神经信号，从而提高B2BC中信息传输中的鲁棒性。

近年来，随着神经网络研究的发展，研究人员致力于解释人类意识产生过程和人工智能（AI）实现过程的内在本质，其中一个研究方向是通过探索人类大脑认知和意识产生过程的规律来促进机器学习技术的发展。现在基于EEG信号本身的数字分析方法[2-3]也不断被提出和完善，如单试次分析等方法，其考虑到了EEG信号在不同受试者之间存在显著差异[4]。这些方法为提取EEG信号可能存在的关联性更强，但形式更为简单的数字特征提供了尝试途径。这与B2BC提取神经信号之后的数字化过程不谋而合。结合两个领域的关联性，对人脑认知过程的分析是具有前瞻性价值的。

格式塔心理学（Gestalt psychology）理论是现代认知学习理论的先驱基础。它是20世纪初由德国心理学家Westheimer W.Kohler 和 K. Koffka 在相似性研究的基础上建立起来的。他们认为，思维是一种整体的、有意义的感知，而不是相互关联的表象的简单集合；主张学习在于构成完形（Gestalt），改变一个完形为另一完形[5]。这种认知过程与目前通过深度神经网络（deep neural network，DNN）进行机器学习的图像识别模式有着本质的不同。

神经网络研究的发展十分迅速，更新更强的算法模型层出不穷，其计算能力和对指定任务的学习能力十分强大。在此基础上，研究人员提出了新的目标，他们的研究重点是使人工智能更加智能，即实现类脑智能。他们希望机器学习不仅能够实现人脑所能做的事情，还要能够像人脑一样解决问题或者像人类一样去认知事物。源自一个神经细胞如何传输信号的原理启发，发展构建出了如今的神经网络；那么整个生物神经网络的连接性质和联动的规律能带给人们的必然是类脑智能化，这不仅是神经网络发展从机械的机器学习过程向意识层面跃迁的契机，也是脑机接口（brain computer interface，BCI）技术进一步发展的必然。通过探索大脑认知行为，有可能探索意识的产生[6]，而不局限于大脑产生了何种意识。

现阶段已有相关工作开展，探索神经网络和人类大脑的生物模式之间的关联[7-17]。因为大脑功能是由不同神经元和大脑不同区域[11]之间的内部相互作用决定的，为了了解大脑对外界刺激的反应，学者们开发了功能网络分析方法分析整个大脑所表现出来的神经信号。大脑结构中神经元之间的空间连接关系是一个复杂的连接模型，该模型长期以来一直作为分析人类大脑活动的拓扑工具。此类研究最初的重点是区分脑电图中容易识别的体感知觉（如冷热感觉、疼痛感觉等）[12]。随后对异常脑电图（癫痫发作）[13]、稳态视觉诱发电位（SSVEP）、运动意图检测[17]和情绪分类[16]进行分析。在以上探究尝试中，拓扑分析方法能实现对不同EEG信号的区分性已经得到了充分证明。近来，Baker等[14]和Been Kim团队[15]对格式塔识别结合机器学习的研究，讨论了机器神经网络的实现和人类大脑的认知过程之间的差异，二者提出了完全相反的结论，矛盾的提出更激励了关于意识水平认知过程的研究。

借鉴前述实验经验，可以充分认识到人类大脑对几何图案整体轮廓的认知面临着局部和全局的问题。因此，本文研究采用能够提供关于任意图[8]的局部和全局性质的定量信息的数学工具——代数拓扑。拓扑数据分析（topological data analysis，TDA）能够提供一系列新的拓扑和几何方法来分析通过EEG信号表现出来的大脑神经网络，其中持续同调是本实验分析的关键方法[18-23]。持续同调分析提供计算网络族中每个复杂图的贝蒂数（Betti number）的有效算法，并对嵌套的复杂同构群在不同网络规模下的演化进行编码。因此，它有助于更好地理解脑电数据，并在EEG信号中存在扰动或噪声时保持分析的稳定性。

2 格式塔完形识别的实验与方法

显示针对格式塔轮廓认知基于持续同调性的拓扑数据分析的神经生理评估过程和方法如图1所示。

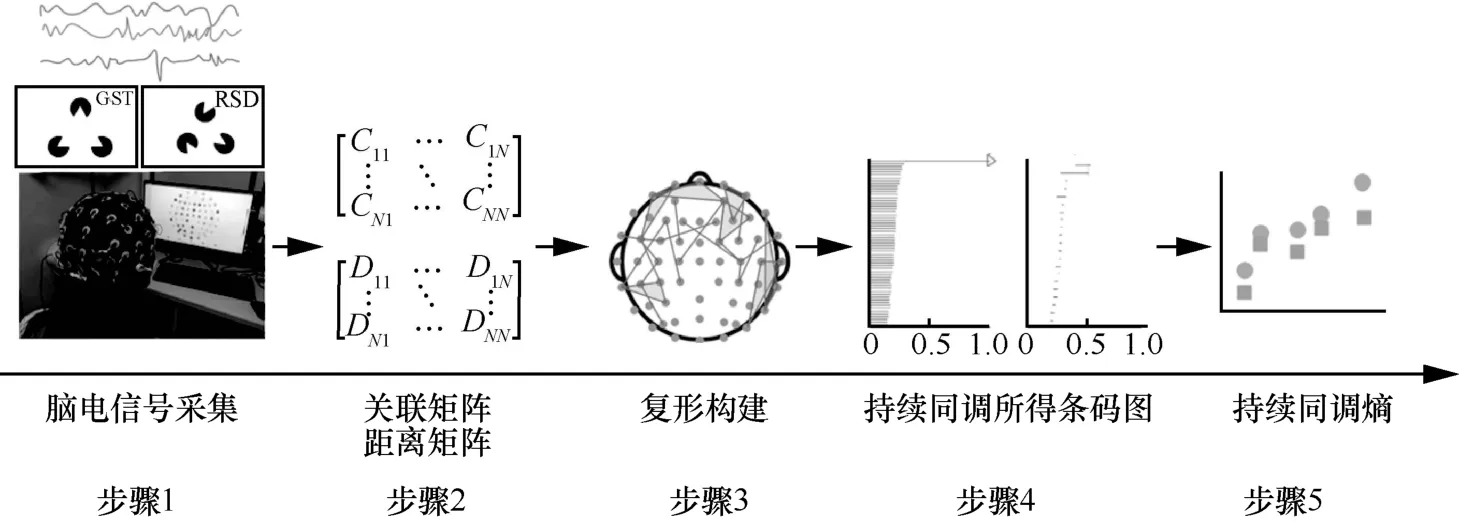
图1 用拓扑数据分析格式塔轮廓认知的神经生理过程和方法

• 在大脑认知过程中，被试者先以固定的间隔重复观看RSD图片，然后以相同的方式观看GST图片。同时利用带有传感电极的脑电帽对EEG数据进行同步采集。

• 使用两种方法计算相关系数（0～1）：一是计算传感器之间的信号的相关系数，通过基于希尔伯特变换的算法构造关联矩阵（C-matrix），另一种是计算标准化之间的欧几里得距离，构建一个距离矩阵（D-matrix）。

• 通过计算所得的邻接矩阵构建Vietoris-Rips复形，采用持续同源法分析不同图片刺激下大脑的神经生理特征，并实现神经信号的数字化过程。

2.1 刺激设定

脑认知实验中使用的两种格式塔图片如图2所示，选择标准三角形轮廓存在与不存在的两种具有代表性的格式塔图片作为刺激：一种是人们很容易识别出三角形轮廓的图片（GST），另一种是随机序列图（RSD）。两种图片的大小和质量保持一致，分辨率都是1 440 dpi×1 080 dpi。为了探究被试者认知过程中意识变化的特点，重复RSD 30次，接着重复GST 10次，以增加样本量，消除潜在的实验误差。

图2 脑认知实验中使用的两种格式塔图片

2.2 实验步骤

对被试者大致介绍实验流程和设备情况后，开始EEG信号的采集，实验流程如图3所示。记录的EEG信号对应整个认知过程中连续的两个阶段。第一阶段是在被试者对RSD没有明确识别出三角形轮廓的情况下收集EEG信号，第二阶段是在被试者从GST中识别出三角形轮廓的情况下收集EEG信号。每一次试次开始时，都从1 s的准备时间开始，然后RSD或GST图像出现10 s，之后出现1 s休息时段，提醒受试者可以休息一下。

图3 格式塔认知实验流程

2.3 实验对象和设备

本实验收集了20名健康志愿者的EEG数据（男性9名，女性11名；年龄19～27岁），被试者视力正常（或矫正为正常）。实验设备为标准的Neuracle 64系统，包括带传感器阵列的64通道脑电帽、带脑电图采集软件的脑电图记录仪和放大器（NSW364）。EEG信号采样率为1 000 Hz，滤波窗口为0.3 ～ 100 Hz的频率范围。

3 EEG数据的处理和分析

神经信号数字化的过程的数据转变：原生EEG信号先经过滤波、试次分割、基线校准截取各个频段的处理后EEG信号（θ波段、α波段、β波段和全波段）；处理后EEG信号经过两种对电极之间关联度基于不同标准的评估计算方式得到两类电极关系邻接矩阵：关联矩阵（C-matrix）、距离矩阵（D-matrix）；对两类矩阵都进行Vietoris-Rips滤值过程构建复形并得出其过程的持久性条码图（barcode）；最后根据条码图计算各自对应事件反应的持续同调熵（PE），对最后的熵值做比较分析。

3.1 EEG信号的采集与预处理

脑电数据采集采用脑电帽采样和脑电下采样，采样频率为250 Hz。通过一组滤波器得到不同波段的脑电信号，分别是波段θ波段（4～7 Hz）、α波段（8～13 Hz）、β波段（14～30 Hz）和全波段（1～45 Hz）。

过滤后的信号中，脑电帽的每个电极信号对应于一组测量点，在FEEG中的表示为每一行。如上所述，两种数据分析方法用于描述大脑认知过程：一个是通过实时计算各电极之间的相位关系构建关联矩阵（基于希尔伯特变换）；另一个是通过为每个测量点定义电极信号相关水平的距离矩阵。

3.2 关联矩阵（C-matrix）计算

（1）经过关键特征提取并且通过预处理得到每个试次时段的信号为：

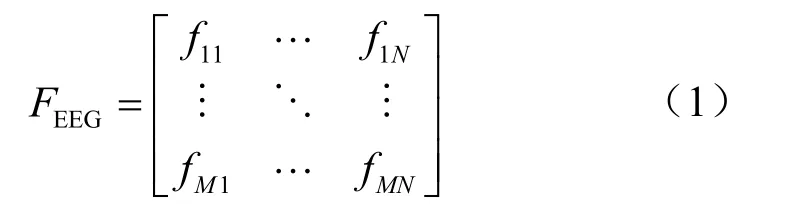
其中，N为数据长度，对应等于采样率乘以时间，M为EEG信号采集的电极数目。

（2）对FEEG中的每一路信号即每一行进行希尔伯特变换[24]，得到H(FEEG)。

（3）采用式（2）得到的H(FEEG)计算每一电极的瞬时相位：

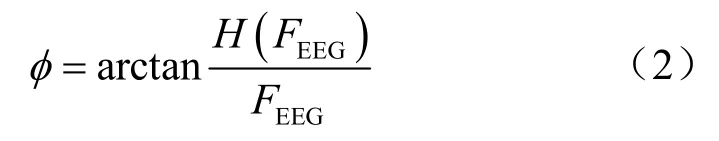
（4）通过式（3）计算关联矩阵对应元素的值，取绝对值，合并得到关联矩阵如式（4）：

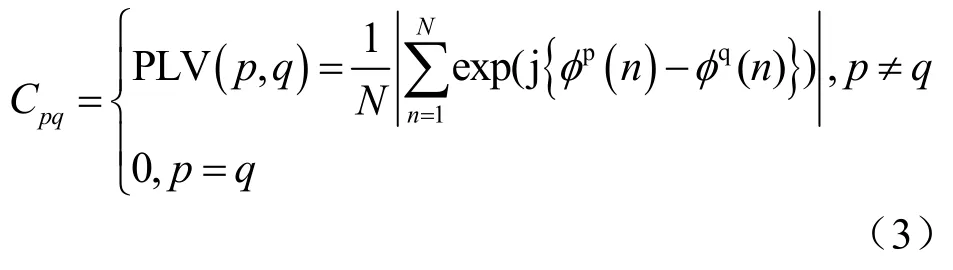
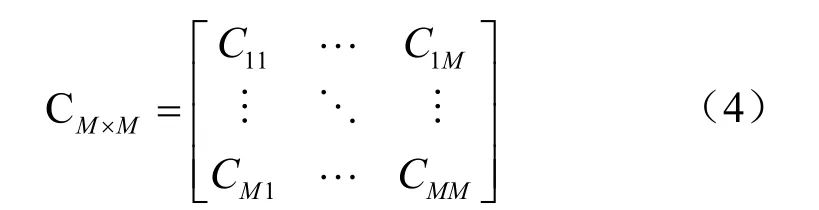
3.3 距离矩阵（D-matrix）计算

脑电帽中每个电极滤波后的信号构成一组采样点G，不同通道电极之间的距离如式（5）计算[13]：

3.4 单纯复形结构

根据计算得到的距离矩阵，相当于预置了各个电极点之间的关联距离或者空间距离，通过Vietoris-Rips滤值构造单纯复形，从零连接到复杂连接点集的滤值过程如图4所示，该过程中连接关系是随着滤值增长而变化的。

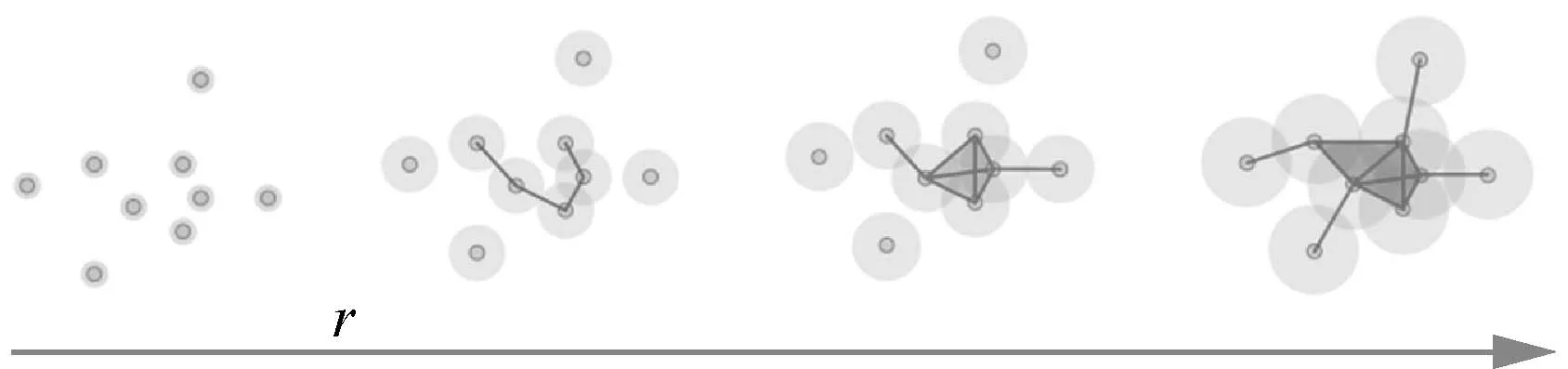
图4 Vietoris-Rips滤值过程

3.5 持续同调分析

持续同调计算拓扑空间中n维孔洞数的代数对象—贝蒂数。本文中，泛型拓扑空间S的贝蒂数由β0、β1和β23个维度组成。β0是S中连接组件的数量，β1是S中环（hole）的数量，β2是孔洞（void）的数量。在滤值过程中，一个k维孔在单纯复形出现的时刻记录为Tstar，而Tend表示k维孔消失。据此，用[Tstar,Tend]定义k维Betti区间长度，持久性条形码（barcode）是其图形表示[8，25，26]。给出0维贝蒂数持续的条形码如图5所示。

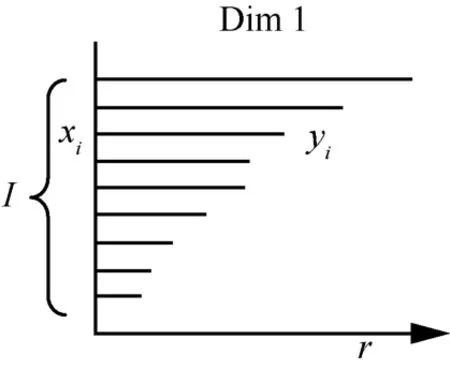
图5 持续的条形码

同调熵利用持久条形码提取拓扑空间特征，从而提供了一种新的熵度量方法。本文设B={(xi,yi)|i∊I}为与拓扑空间S过滤相关的持久条形码，其中，i为索引集。因此，滤值后的单纯复形的持续熵H的计算式为：

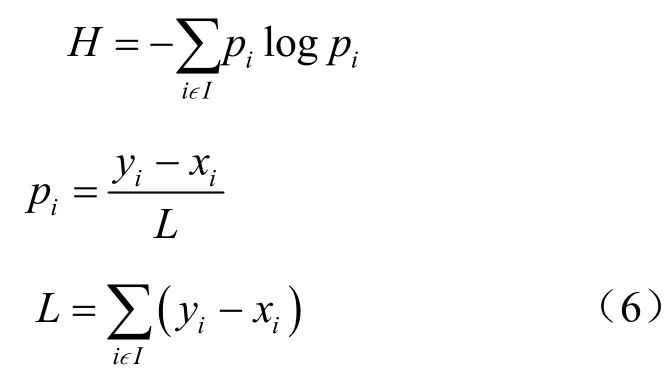
之后对H进行归一化得作为EEG数据的持续同调特征。

其中，lmax是持久条形码图中的最大间隔。

4 结果分析与讨论

通过Vietoris-Rips滤值构建了RSD/GST图片诱发的EEG数据的拓扑模型。大脑不同区域活动与图像形状和轮廓感知之间的关系在图6中显示了整体的情况。基本上，当被试者观察RSD图像时，大脑活动涉及的区域更多，但特征不显著，总体电平值较为均衡，但当被试者感知到GST图像时，脑部会有清晰的反应区域，特征更显著。因此，本文假定模糊的认知目标使任务更困难，导致更多的心理活动。图6显示了人类对形状轮廓的感知与包括格式塔认知在内的高级认知过程之间的相关性。这些结果验证了本文的分析方法在描述EEG信号和形状认知之间的内在相关性方面的有效性，并且本文的方法更接近于实际的生物反应过程。

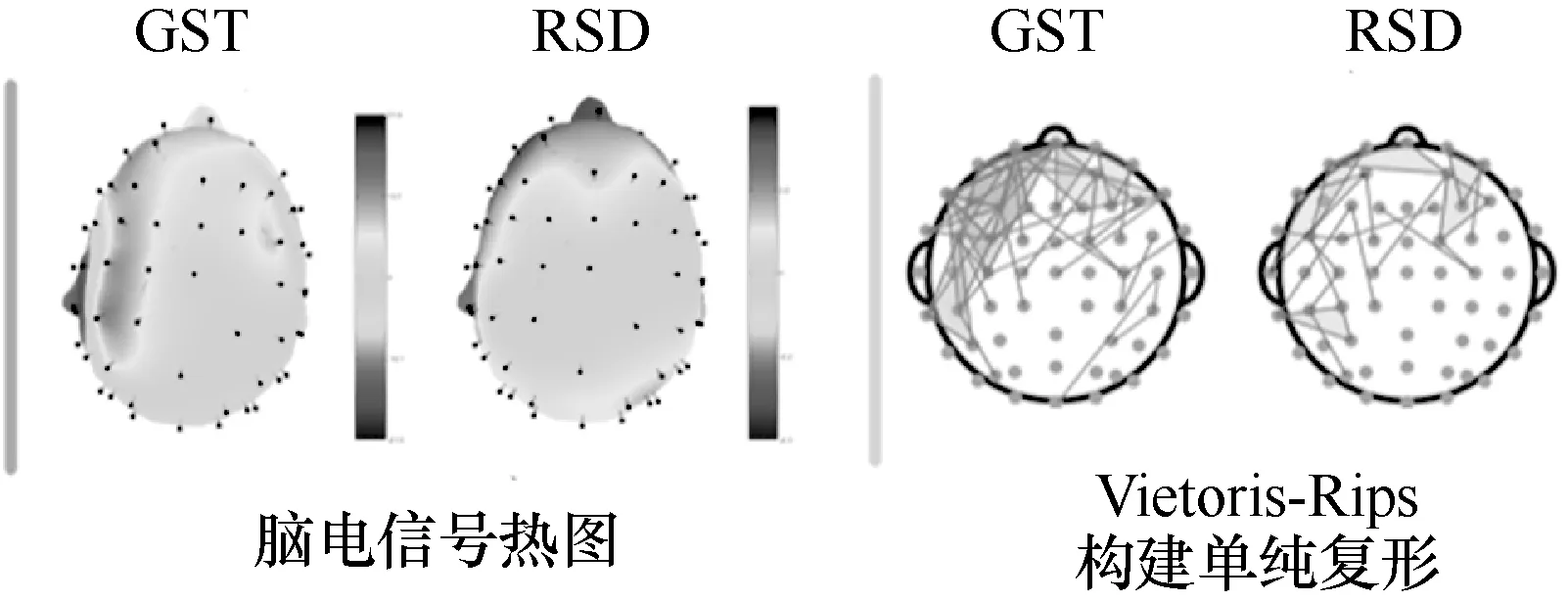
图6 脑电图映射和Vietoris-Rips单纯复形

实验表明RSD和GST实验之间存在显著差异。在不知道实验目的的情况下，被试者首先观察了RSD图片，这些图片是无序、随机混乱的。因此，在每个试次中显示总体EEG信号水平处于较为均衡的状态，而被试者对GST图片所包含的形状信息在2 s内就产生了直观反应，之后EEG信号水平趋于稳定。

采用持续熵（PE）作为整体实验的判别标准，两类认知行为判别度的范围、平均值和最大值见表1。关联矩阵和距离矩阵在各频带对事件分类的平均判别率均大于70%，最佳判别率分别达到90%和85%。

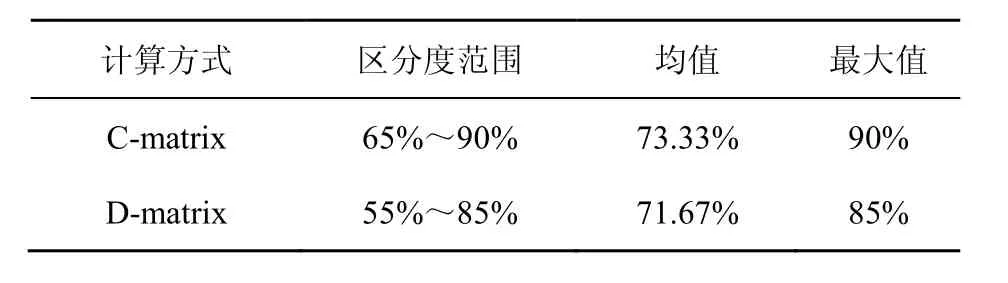
表1 判别标准

关联矩阵和距离矩阵计算的持续同调熵比较如图7所示，分别给出了两种不同矩阵计算方法得到的持续同调熵（PE）的性能和比较。通过对20名受试者的统计分类比较，可以看出，两种方法都清晰地描述了两种脑认知情境下两种拓扑模式在持续同调熵上的特征分离。

本文进一步绘制了GST和RSD值的对比图，如图8所示。

由图7和图8可以得出直观的实验数据结果：

图7 关联矩阵和距离矩阵计算的持续同调熵比较

图8 关联矩阵和距离矩阵计算的GST值和RSD值对比

• 通过关联矩阵计算得出：在θ波段（4～7 Hz）、α波段（8～ 13 Hz）、全波段（1～ 45 Hz）的实验中，绝大多数样本的GST诱发的EEG信号拓扑计算所得的持续同调熵都高于RSD诱发的EEG信号。

• 通过距离矩阵计算持续同调熵的情况则相反。在上述各波段的表现为RSD诱发的EEG信号的持续同调熵高于GST诱发的EEG信号。

从测量和分析结果可以明显看出，具有显著差异的波段是α波段和θ波段，这与整体原始信号对应的趋势是一致的。但是在β波段，两种方法表现出的分类结果是相似的，RSD和GST比较的趋向是一致的，关联矩阵和距离矩阵计算的持续同调熵在β波段的结果对比如图9所示。

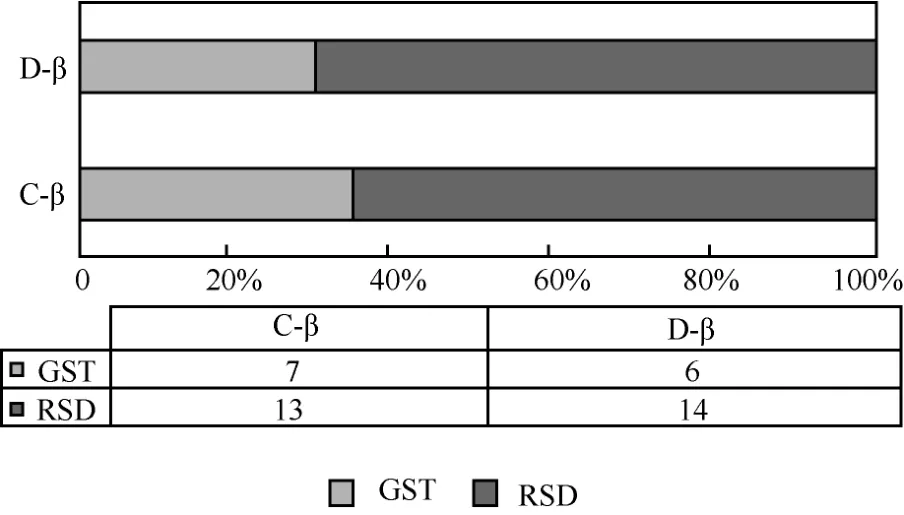
图9 关联矩阵和距离矩阵计算的持续同调熵在 β波段的结果对比

作为总结，本文提出了一种神经生理学方法，通过EEG信号评估认知格式塔图像的形状和轮廓。当被试感知到RSD图像时，与GST图像相比，更多的大脑区域参与到认知过程中。在这种情况下，可以理解人脑处于一种随机且混沌得状态。采用TDA方法提取由形状轮廓诱发的EEG信号的生理特征。结果表明，GST图像诱导的脑电数据在β波段下，两种计算方法得到的持续同调熵值均低于RSD图像。在α波段和θ波段以及1～45 Hz全波段的持续熵值一致表明：

（1）关联矩阵计算：PEGST＞PERSD；

（2）距离矩阵计算：PEGST＜PERSD。

与基于诱发电位的传统神经生理学方法（需要特定的实验范式）相比，本文的方法提供了一种可概括的方法，可以从整个大脑的EEG信号中提取整体信息，在保存整体和局部特征的情况下完成数字化特征提取。本文的方法不仅关注大脑对外部刺激的反应，还关注设计用来标准化和提取数字特征的算法，这些特征可以可靠地分类，并代表不同的认知感知。代数拓扑用于解释人脑中不同神经区域之间的协调关系的工作，可以为复杂神经网络协同工作的分析方法提供启发。将复杂的神经网络模型的维数降为一维持续熵来衡量其特性。与此同时在B2BC的技术流程中可以有效提供神经信号数字化的操作方法。

上述结果可以直观地表明，某些特定B2BC交互场景中，具体的人脑神经信号转化为一个特征信号（PE）的可靠传输是可以实现的。

5 结束语

本文提出利用脑网络的持续同源性对人类高级认知过程神经信号进行生理学评估并且提取具有可分性的数字特征（PE）的方法，可以作为B2BC实现神经信号数字化的一种工具手段。该方法将脑电采集与传统的格式塔心理学测试过程相结合，获取认知相关的神经信息，并通过代数拓扑分析获得对有无清晰轮廓的大脑反应的生理学意义特征。验证实验结果表明对于形状轮廓认知这一实验场景，采用两种脑电关联性特征提取的矩阵所计算的PE都具有可观的可分性。在未来6G无线通信中，要实现结合BCI的高级设备的无线使能，于B2BC而言，准确且稳定的数字化特征的提取是关键，也是实现该技术的基础。用持续同调分析方法来进行神经信号的数字化，可以实时动态地计算提取EEG信号的数字特征，既极大地压缩了数据传输量，又保证了信息传输的稳定性。在6G支持的更高速更稳定的无线通信技术的支持下，B2BC乃至脑对脑网络的形成都将在此基础之上得以实现。

由于本文关注的是格式塔轮廓认知的一个具体案例，未来的研究会扩展到分析不同的认知目标，如颜色或内容等其他类目的意识认知行为，从更多角度验证TDA解释认知过程的可行性。区别于以往的EEG信号分析实验，本工作是首次以数字化神经信号特征的方式解释人类大脑意识模式，是从“感觉”到“意识”的探索。此外，深入掌握大脑反应过程中大脑神经网络的联动行为，可能会启发人们构建新的人工神经网络结构，这需要进一步的研究和实验。

综上所述，本文提出了数字化人脑对图形轮廓形认知过程神经信号的方法，并通过实验验证了该方法的实用性和有效性，这对B2BC技术实现和DNN结构的发展具有启发意义。