基于电力大数据的中国工业增加值现时预测

彭放，彭高群，祁亚茹，刘甜甜，周晓磊

（1. 国家电网有限公司大数据中心，北京 100031；2. 清华大学社会科学学院，北京 100084）

1 引言

作为国民经济的“晴雨表”，电力数据可以及时、客观地反映经济发展的真实情况。伴随着电力信息化的发展，如何充分挖掘电力数据的价值服务于经济社会发展、政府政策制定成为关注的重点。工业增加值是衡量实体经济运行状况的重要指标，对其进行更加及时、准确地预测有助于政府更快、更准确地了解经济形势，为经济政策制定提供可靠的依据，同时也将有助于企业和个人准确把握经济形势并进行决策。在当前经济下行压力增加、不确定性加剧的环境下，及时准确地预测工业增加值显得尤为重要。为此，本文以工业增加的现时预测为出发点，充分挖掘电力大数据在现时预测中的作用。现时预测最初被用于气象领域，近年来被引入经济领域，是对当前经济形势的预测，其基本原理为在官方发布相关统计数据之前，充分挖掘先行高频数据的信息预测当前经济形势[1]。

当前关于中国工业増加值预测的研究相对较少，且主要基于所选择的若干传统统计指标进行，如利用社会消费品零食总额、广义货币数据对工业增加值进行预测[2]，基于构建的民营企业信用利差指数对工业增加进行预测[3]。在宏观经济传导机制愈发复杂、工业增加值影响因素更加多元的情形下，恰当的预测模型应当包含大量的解释变量以充分利用有价值的信息，仅利用少数几个变量较难获得精准的预测。此外，传统统计数据发布得滞后致使预测时难以利用经济活动的当前信息，而电力大数据与经济活动密切相关且实时可得，可提供经济活动的当前信息弥补传统统计数据的不足。因此，综合利用电力数据和传统统计数据可能得到更加准确的工业增加值预测结果。然而，这不可避免地引出工业增加值预测中传统数据和电力数据的关系问题，即工业增加值预测中电力数据是否可以替代传统数据，较之于成熟的统计数据电力数据的用处不大，两者是否可以相互补充。该问题同样也是大数据时代基于新兴数据进行宏观经济预测时可能碰到的问题，但当前却鲜有文献对此进行研究。本文设计了5类模型以探究工业增加值预测中统计数据与电力大数据的关系，同时采用多种预测方法进行预测以期获得更佳的预测效果。

2 研究设计

2.1 预测模型

为充分探究上述工业增加值现时预测中传统经济统计数据和电力数据的关系问题，设计两类数据结合的5种方式：其一，仅利用传统统计数据进行预测；其二，以传统经济统计数据预测为主，以电力数据预测为辅；其三，仅利用电力数据进行预测；其四，以电力数据预测为主，以统计数据预测为辅；其五，同时无差别地利用经济统计数据和电力数据进行预测。本文基于这5种结合方式构建了如下5类相应的预测模型。

模型1：

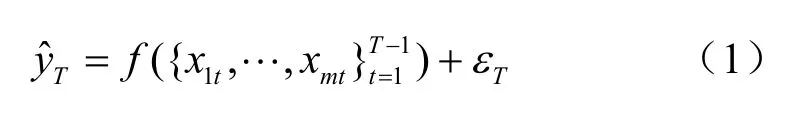
本模型分析仅利用传统经济统计数据预测y的预测效果。模型中表示在T期预测时可用的信息集，由于经济统计数据的发布存在滞后性，所以信息集中仅包含T−1期及其以前的统计数据信息。

模型 2：

本模型利用传统经济统计数据和电力数据预测y，在预测时以统计数据预测为主，以电力数据预测为辅。模型中表示在T期预测时可用的信息集，由于电力数据实时可得，所以预测第T期y值时可用到电力数据的当期值，即第T期的值。表示利用电力数据具有但不包含于统计数据中的信息进行预测。

模型3：

本模型分析仅利用电力数据预测y的预测效果。模型中表示在T期预测时可用的信息集，由于电力数据实时可得所以预测时可用到电力数据的当期值。

模型4：

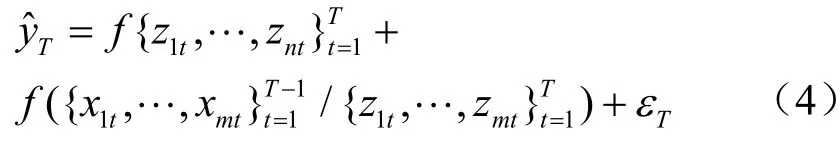
本模型利用传统经济统计数据和电力数据预测y，在预测时以电力数据预测为主，以统计数据预测为辅。模型中表示在T期预测时可用的信息集，表示在利用统计数据进行预测前先将统计数据中包含的电力数据信息去除。

模型5：

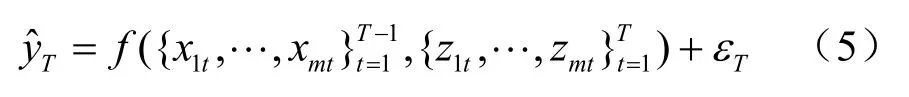
模型5综合利用传统统计数据和电力数据预测工业增加值，其与模型2、模型4的区别在于本模型在预测中无差别地对待两类数据。

2.2 预测方法

面对众多的解释变量，如何有效地利用其包含的信息是影响预测结果的关键问题。采用参考文献[4]提出的扩散指数（diffusion index，DI）算法、参考文献[5]提出的Bagging算法以及参考文献[6]提出的Boosting算法进行预测。

2.2.1 DI算法

DI算法为数据丰富环境下的常用预测方法，下面对扩散指数方法做简要介绍。对数据集，首先，基于模型提取的共同因子ft=(f1t,…,fqt)，然后利用提取的因子ft构建如下模型并进行预测：

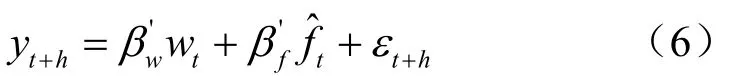
其中，yt为预测目标变量，为估计的因子向量，tw为可观测向量。对因子个数q的估计可利用如下信息准则[7]：

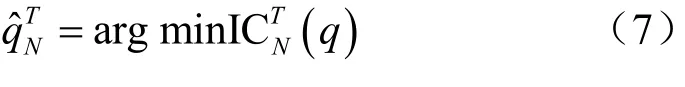
其中：

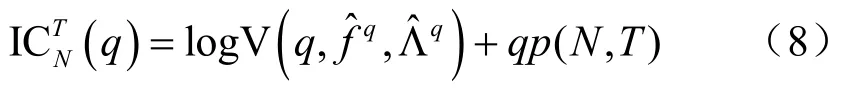
可以看出DI算法分为两步：首先，从众多变量构成的信息集中提取因子；然后，将因子纳入预测模型进行预测。第一步的因子提取既实现了降维又充分利用了大量变量的信息，但在提取因子时并未考虑信息集中的变量是否有助于预测，这可能导致纳入模型的因子不仅无助于预测反而降低了预测精准度。为此，采用Bagging算法[5]、Boosting算法[6]解决上述问题以提高工业增加值的预测精度。

2.2.2 Bagging算法

Bagging为bootstrap aggregation的缩写，由Breiman提出[8]。该算法基于提取的bootstrap样本训练模型并进行预测，上述过程重复若干次后将所有预测值的均值作为最终预测结果。近年来，部分学者将其用于经济时间序列的预测[9-10]，本文参照参考文献[5]的做法进行预测，相应Bagging算法可表述为：

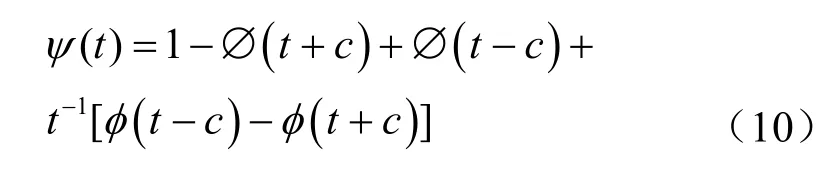
其中，∅为标准正态分布函数，φ为标准正态密度函数，c为预先设定的值。

2.2.3 Boosting 算法

Boosting算法是一族可将弱学习器提升为强学习器的算法，一般可表示为如下形式：

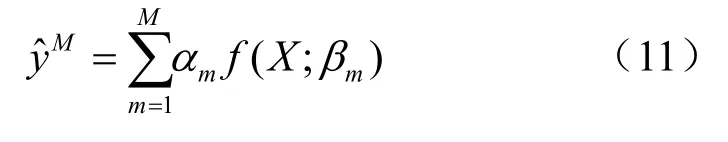
其中，αm为权重，f(X;βm)为定义在信息集X上函数。参考文献[11]提出的Boosting算法在每次迭代中仅利用一个变量，使得Boosting算法可适用于存在大量变量且数据满足独立同分布的场景，参考文献[6]进一步优化了参考文献[11]的算法，利用Boosting算法处理时间序列问题。采用参考文献[6]提出的Component-Wise L2 Boosting算法挑选用于预测的因子，若将Boosting算法作用于因子后得到的值记为，那么最终预测值为：

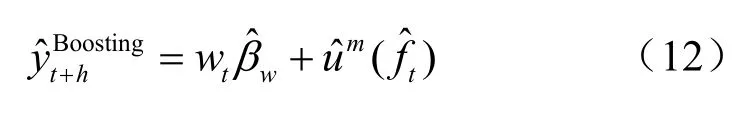
3 实证分析

3.1 数据说明与处理

本文选择的数据分为两类：传统经济统计数据和电力数据。所有变量均采用同比增长率，时间跨度为2014年1月至2017年12月。传统统计数据主要包括居民消费价格指数、名义有效汇率、上证交易所和深证交易所各类指数、商业信心指数、贸易指数、货币供应、存款、宏观经济景气指数等42个变量，这些数据来源于CEIC数据库。电力数据为不同行业购电量数据的同比值，相关数据来源于国家电网大数据中心。

从信息集中提取因子要求信息集中的变量必须为平稳变量，为此本文采用常用的增广迪基−富勒（augmented Dickey-Fuller，ADF）单位根检验方法检验变量的平稳性。ADF检验通过对如下3个模型的检验进行。

其中，Yt表示被检验的时间序列，Δ为差分算子，即ΔYt=Yt−Yt−1。上述3个模型的零假设均为H0：δ= 0，即时间序列是不平稳的。上述3个模型只要有一个模型拒绝了零假设就认为时间序列是平稳的，如果3个模型都不能拒绝零假设则认为时间序列非平稳。对于被检验变量，若检验表明其不平稳，则对其取差分并再次检验其平稳性；若变量差分后仍不平稳，则再次进行差分。限于篇幅原因，本文不给出变量平稳性的检验结果及对非平稳变量的差分情况。

3.2 基准模型与效果评估

本文选择自回归滑动平均（auto-regressive integratedmoving average，ARIMA）模型作为基准模型，采用均方预测误差（mean squared forecast error，MSFE）测度模型的预测效果，MSFE的计算式如下：

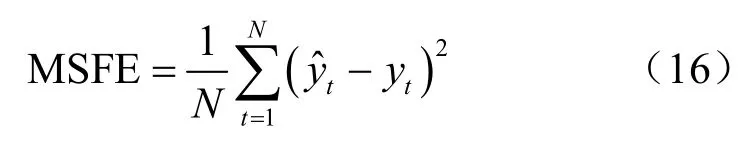
其中，MSFENBM为非基准模型的均方预测误差，MSFEBM为基准预测模型的均方预测误差。rMSFE小于1，则说明非基准模型较基准模型有更好的预测效果，而且比值越小说明非基准模型的预测效果越好。

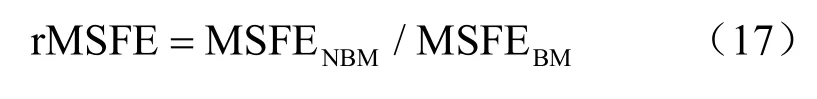
3.3 结果比较与分析

本文在估计模型和进行预测时采用了移动窗口和累积窗口两种方法。累积窗口法，即在下一期预测时，将前面所有样本（包括上一期）的真实值作为训练集放入估计模型中，训练集逐期增加。移动窗口法，就是固定训练集观察值的长度，每往后预测一期，训练集往后移动一期。本文选择2014年1月至2017年6月期间的数据作为训练集，选择2017年7月至2017年12月期间的数据作为预测集。

为充分探究电力数据在工业增加值预测中的作用，报告基于电力数据指标不同分类与传统统计数据组合的预测效果进行了分析，表1至表9分别呈现了不同模型与数据组合预测工业增加值的rMSFE。考虑电力数据实时可得的特点，本文采用两种方式利用电力数据信息：其一，仅利用电力数据当期信息，即表1至表9中数据无滞后；其二，不仅利用电力数据的当期信息还利用其滞后信息，即表1至表9中数据有滞后。

表1呈现了基于居民和企业总用电数据与统计数据现时预测工业增加值的rMSFE，表2呈现了利用全行业用电一级指标数据与统计数据现时预测工业增加值的rMSFE。由表1和表2可以发现以下结论。

表1 基于居民和企业总用电数据与统计数据预测工业增加的rMSFE

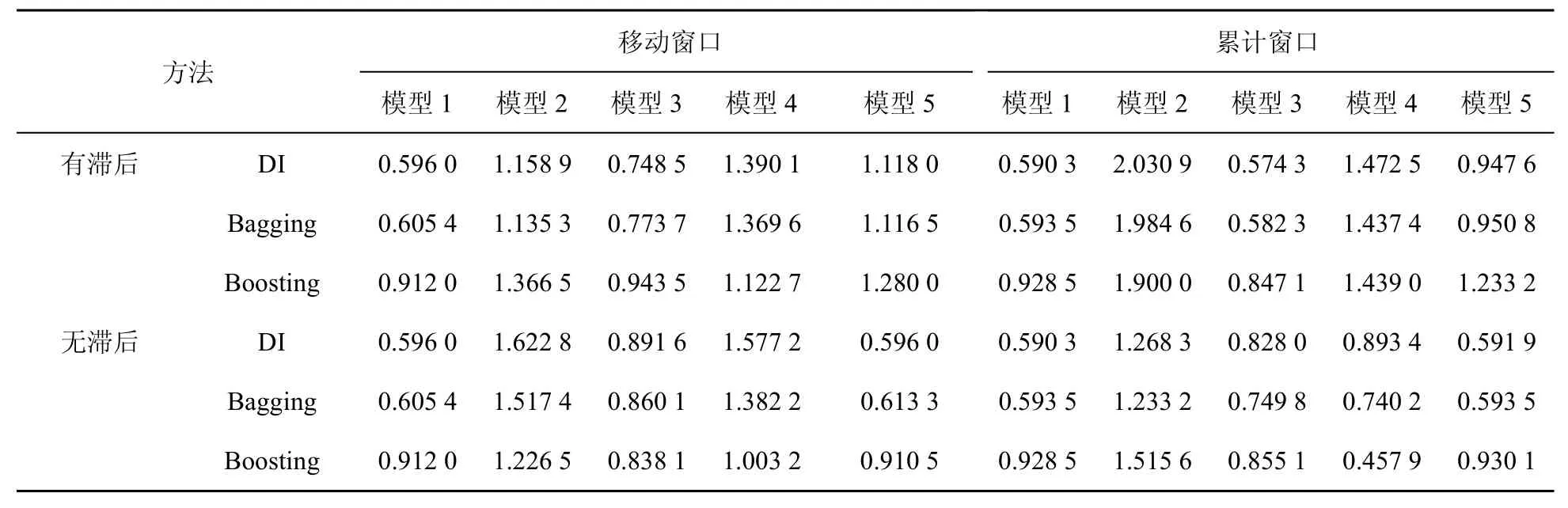
表2 基于全行业用电一级指标数据与统计数据预测工业增加的rMSFE

（1）对模型1，TMSFE均小于1，这意味着利用ARIMA模型的预测结果并不是最优的，基于大量传统统计数据的预测效果要优于ARIMA模型。

（2）对模型2到模型5，与仅利用电力数据当期信息的预测效果相比，利用电力数据当期和滞后信息的预测效果更好。为此本文仅就存在滞后信息的情况进行分析。

（3）对模型3，其在表2中的预测效果要优于在表1中的预测效果，而且前者的效果要优于ARIMA模型，后者的预测效果与ARIMA模型相比较差。这意味着相对于居民和企业总用电数据，电力全行业一级指标用电数据包含更多有助于工业增加值预测的信息。

（4）对模型2，可以发现利用电力全行业一级指标以及居民和企业总用电量的预测效果均不优于模型1，而且利用电力数据全行业一级指标的预测效果与利用居民和企业总用电量的预测效果相比更优，这意味着居民和企业总用电量包含更多无助于工业增加值预测的信息。

（5）对模型4，可以发现其大多数情况下预测效果比模型3差，这表明在剔除相应电力数据信息后，统计数据剩余信息含有较多无助于工业增加值预测的噪音。对模型5，由于无差别地利用两类数据，且表1、表2所用电力数据指标个数分别为1和8，基于因子提取的机理可推断模型5的预测效果在表1中其接近于模型1，在表2中其接近于模型3。

上述分析表明，就工业增加值的预测而言，电力数据全行业一级指标比居民和企业用电总量指标含有更多有用的信息，但仍包含较多无助于预测的信息，为此接下来的分析将减少电力数据指标涉及的行业。表3、表4分别给出了利用第二产业总用电数据与传统统计数据、工业总用电数据与传统统计数据现时预测工作增加值的rMSFE。观察表3、表4可以发现以下结论。

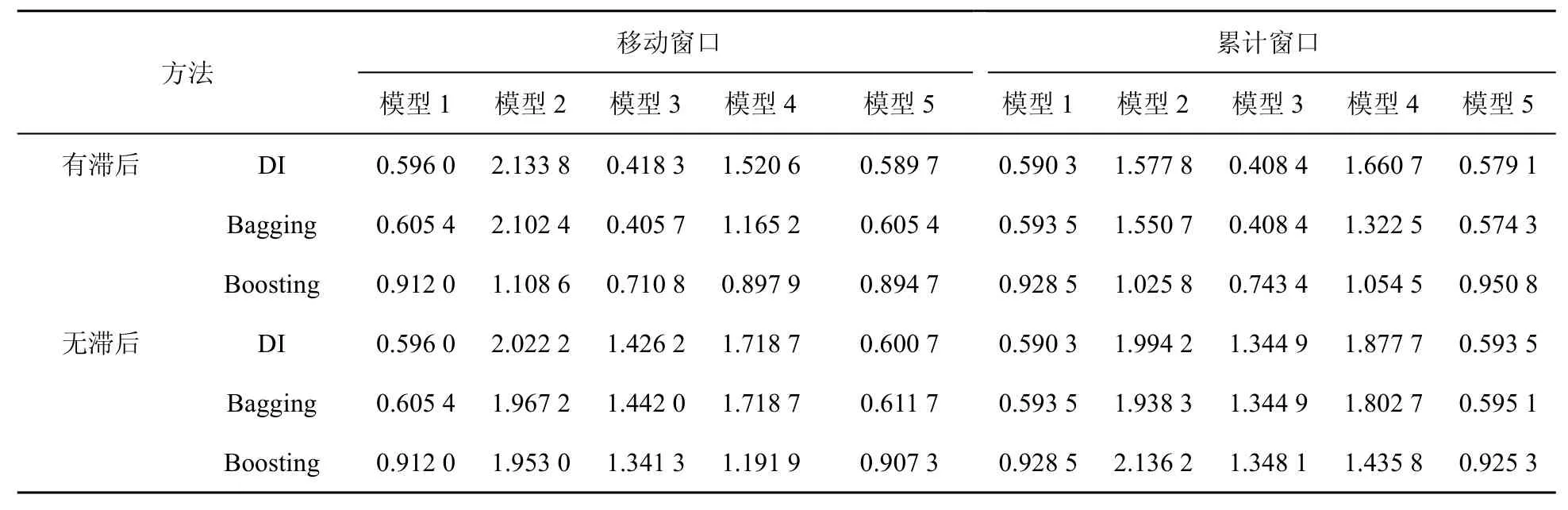
表3 基于第二产业总用电数据与统计数据工业增加的rMSFE

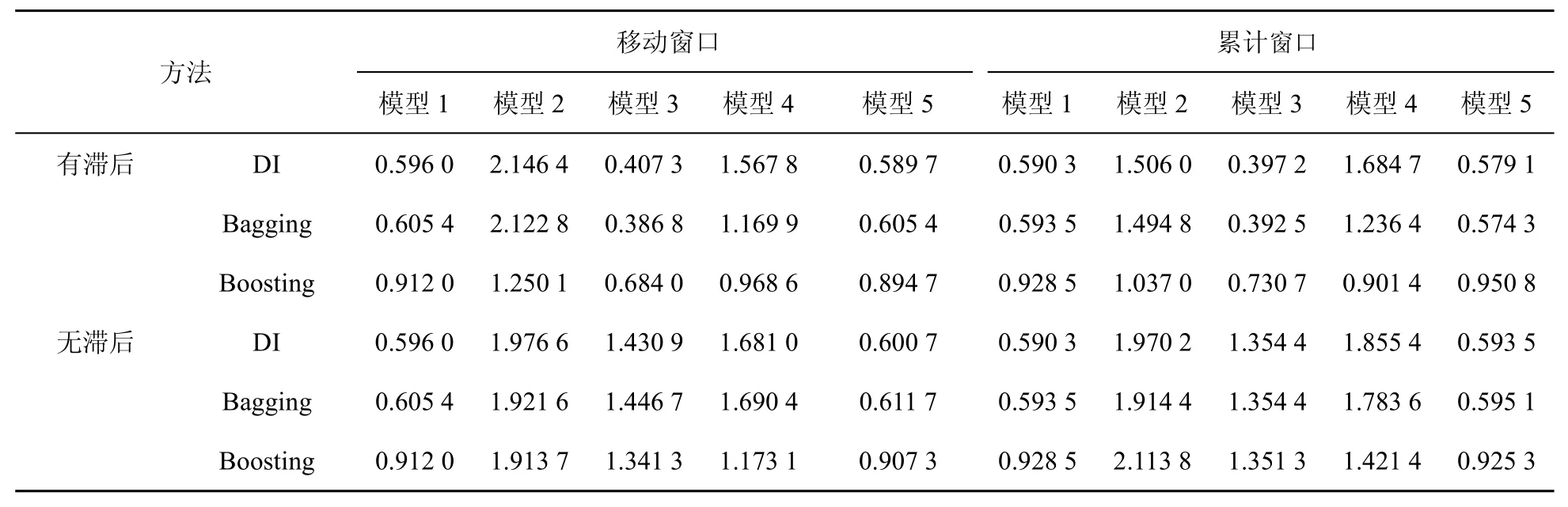
表4 基于工业总用电数据与统计数据工业增加的rMSFE

（1）对模型2到模型5，较之于仅利用电力数据当期信息的预测效果，利用电力数据当期和滞后信息的预测效果更好。这意味着第二产业总用电数据、工业总用电数据的历史信息较之于当期信息具有更好的预测作用，具有领先性。故下面仅就存在滞后的情况进行分析。

（2）对模型3，在表3、表4中rMSFE均小于1，这表明其预测效果均优于ARIMA模型。此外，由模型3在表4中具有更好的预测效果可知，工业总用电数据比第二产业总用电数据包含更多有助于工业增加值现时预测的信息。

（3）比较模型1和模型3可知，模型3具有更好的预测效果，这表明较之于统计数据，第二产业总用电数据或者工业总用电数据含有更多有助于工业增加值预测的信息。

基于上述分析，工业总用电数据相对于第二产业总用电数据含有更多有助于工业增加值现时预测的信息。考虑工业部门包含不同行业，接下来探究工业部门中不同行业用电数据现时预测工业增加值的能力，预测结果如表5至表9所示。表5、表6分别给出了基于工业部门用电二级指标数据与统计数据、工业部门用电一级指标数据与统计数据的预测效果。观察表5、表6可以发现以下结论。

（1）对模型2到模型5，用电力当期及滞后期数据的预测效果更好。这同样表明相关电力数据的历史信息比当期信息具有更好的预测作用，所以本文仅就存在滞后的情况进行分析。

（2）比较模型3与模型1，显然前者的预测效果优于后者。这意味着较之于统计数据，表5、表6所用电力数据含有更多有助于工业增加值预测的信息。这点通过比较模型2与模型1、模型4与模型3的预测效果也可以看出。

对比表4、表5、表6中模型3的预测效果可以发现，尽管都利用了工业部门的电力数据信息，但表6中模型3的预测效果却更好，即利用工业部门用电一级指标数据的预测效果要优于利用工业部门总用电数据及工业部门用电二级指标数据的预测效果。结合因子分析的机理，认为这可能源于工业部门中部分行业的用电数据无助于工业增加预测。故接下来将统计数据分别与表6中所用工业部门用电一级指标（即矿业、制造业、电力、燃气及水的生产和供应业3个行业各自用电总量数据）结合进行工业增加值现时预测，相应的预测结果见表7、表8、表9。通过比较可以发现以下结论。

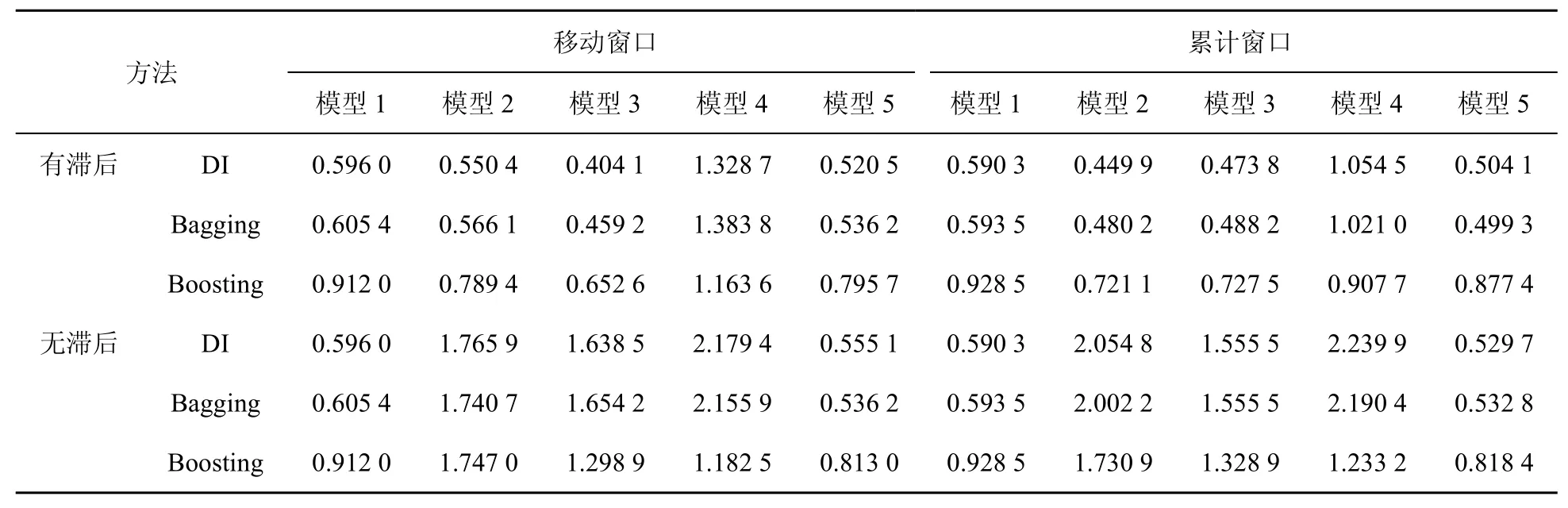
表5 基于工业部门用电二级指标数据与统计数据工业增加的rMSFE

表6 基于工业部门用电一级指标数据与统计数据工业增加的rMSFE

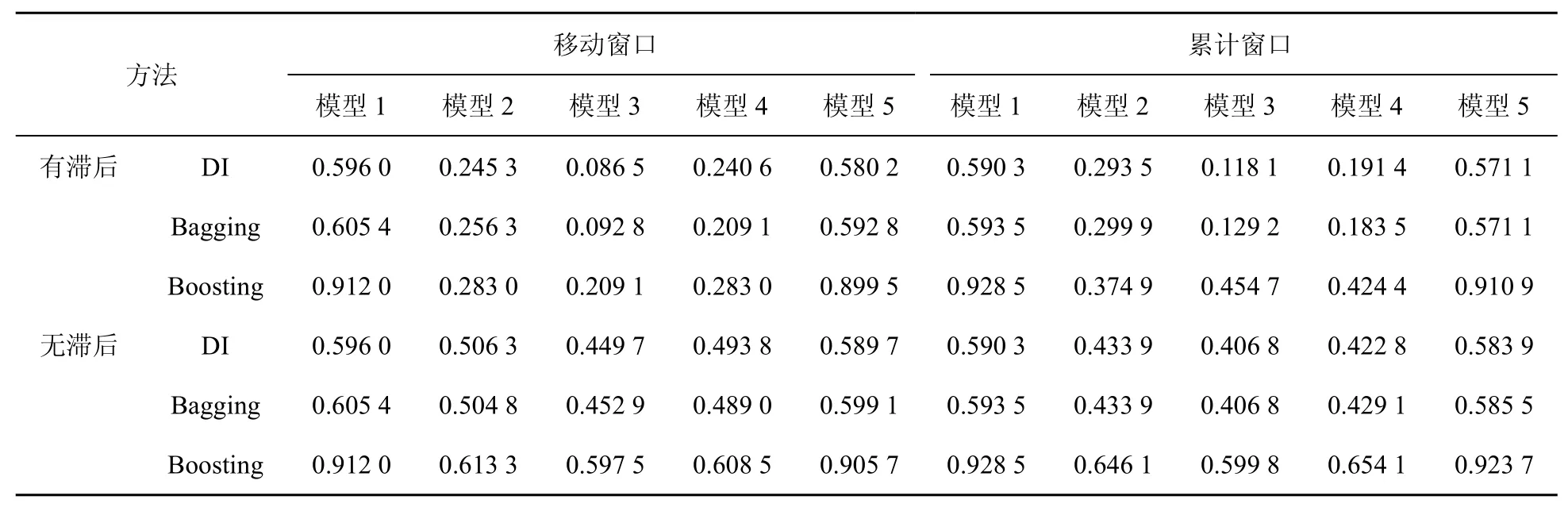
表7 基于采矿业总用电数据与统计数据工业增加的rMSFE

表8 基于制造业总用电数据与统计数据工业增加的rMSFE

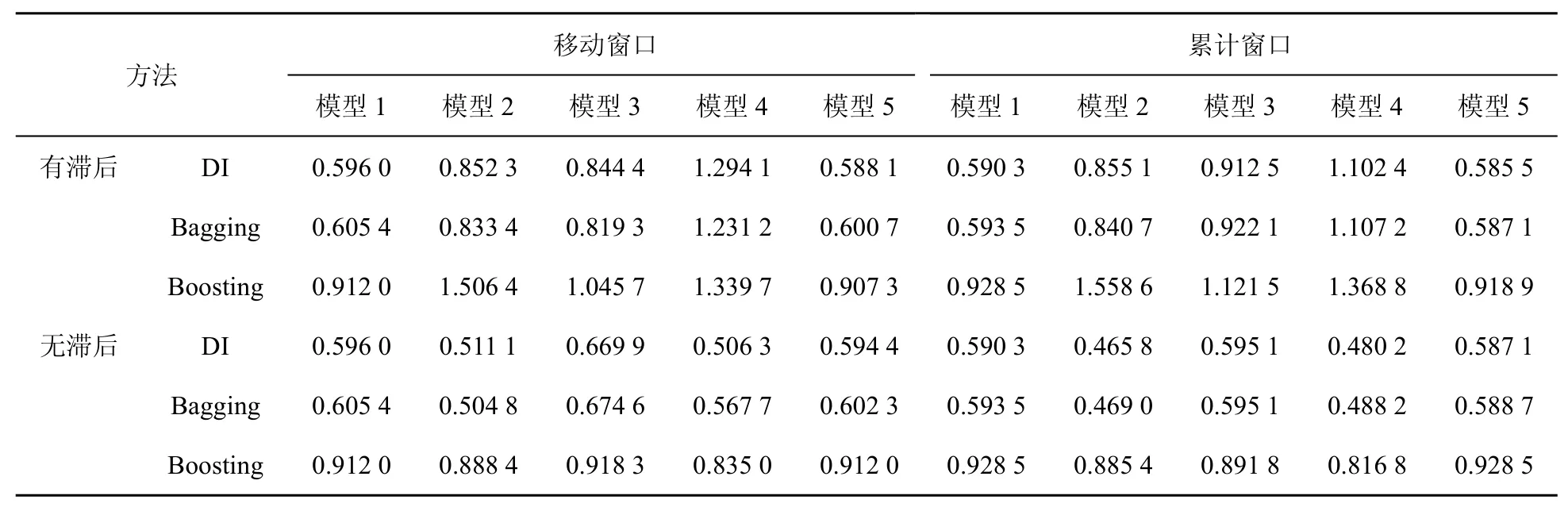
表9 基于电力、燃气及水的生产和供应业总用电数据与统计数据工业增加的rMSFE

（1）对模型2到模型5的预测效果，在表7和表8中利用电力数据当期及滞后期信息的预测效果较之于仅利用电力数据当期信息的预测效果更优，但在表9中则仅利用电力数据当期信息时的预测效果更好。故接下来的分析对表7和表8仅讨论利用电力数据当期及滞后信息的情形，对表9仅讨论利用电力数据当期信息时的情形。

（2）对模型3，其在表7、表8、表9中的预测效果依次递减；模型3在表6中的预测效果明显地弱于其在表7 中的预测效果，但优于其在表8、表9中的预测效果。

（3）对于模型1与模型3，可以发现在表9中前者的预测效果明显优于后者，而在表6、表7及表8中后者的预测效果优于前者，特别是在表7中更是如此。

上述关于模型3、模型1在表6、表7、表8及表9中预测效果的分析表明利用电力、燃气及水的生产和供应业电力数据与统计数据的组合可能不是现时预测工业增加值的最佳组合。此外，在表7中模型2的预测效果优于模型1，而在表8中除Boosting算法外模型2的预测效果并不优于模型1，这在一定程度上表明采矿业总体用电数据去除统计数据信息后仍含有较多有助于工业增加值预测的信息，而制造业总体用电数据在去除统计数据信息后所含有助于工业增加值预测的信息相对较少。

以上部分基于表1至表9中的rMSFE分析了DI、Bagging、Boosting算法与两类数据不同结合方式的预测效果，图1给出了上述各表中移动窗口下3种算法各自的最佳预测值曲线，以更加直观地呈现不同预测方法及数据结合方式的预测效果。观察图1可以发现，表3、表4、表6、表7中各预测方法的预测值曲线与工业增加值实际值曲线趋势一致，预测残差相对较小，而且就预测值曲线趋势和预测残差来看，基于DI算法的预测曲线相对更优。

综合上述分析可以发现，就工业增加值的现时预测而言，第二产业、工业、采矿业、制造业的总体用电数据均有较好的预测效果，而且采矿业总体用电数据与统计数据的组合是相对更优的数据组合。就预测方法而言，DI的预测效果要优于Bagging、Boosting，这或许与所用数据有关。此外，较之于仅仅利用电力数据当期信息，利用电力数据当期及滞后期信息可实现更好的工业增加值现时预测效果。

4 结束语

伴随着人类社会迈入大数据时代，部分学者尝试利用新兴大数据进行宏观经济预测。新兴大数据与传统经济统计数据各具优劣，但现有的宏观经济预测研究或者侧重对一类数据的挖掘应用，或者对两类数据无区别地使用，涉及对这两类数据关系的探讨及区别对待的研究较少。电力数据作为经济发展的“晴雨表”，与经济活动密切相关，但鲜有文献探究电力数据在宏观经济预测中的价值。本文提出了电力大数据与经济统计数据在宏经济预测中相结合的5种方式，采用DI、Bagging、Boosting等大数据预测算法，对工业增加值这一重要宏观经济指标进行了预测，探究了在工业增加值预测中如何有效地利用电力大数据与经济统计数据两类信息以获得更加及时、准确的预测结果。研究结果表明，基于选择出的恰当电力指标，可以得到更加及时、准确的工业增加值预测结果。本文的研究可为宏观经济预测中如何有效利用新兴数据和经济统计数据两类信息提供有益的借鉴与启示。