基于卡尔曼滤波的机器人力控制

2021-08-13王宪伦孙旭祥丁文壮段奕林

机械制造与自动化 2021年4期

王宪伦，孙旭祥，丁文壮，段奕林

(青岛科技大学机电工程学院, 山东青岛 266061)

0 引言

随着社会需求的不断提升，机器人已经不再局限于在特定环境下进行简单作业。机器人应用领域也在不断扩展，像公共服务领域的服务机器人，医疗领域的手术机器人，康复机器人等。这些领域都要求机器人能够对复杂的工作环境做出正确快速的响应，所以机器人与环境之间的交互能力就显得尤为重要。仅从机器人已经广泛应用的工业领域来讲，其作业形式也日趋多样化，像打磨、抛光、装配等接触式作业除了有位置精度要求外，还需要对机器人与工件的接触力进行控制。因此，设计出能够适应复杂且未知环境的机器人力控制方法也就受到了越来越多的重视。

文献[1]结合机器人位姿、力和力矩混合控制和Kalman状态观测器的优点，提出了对系统干扰具有较强抑制能力的力/位混合控制方法。文献[2]在室内复杂环境下，采用扩展卡尔曼滤波器(EKF)对机器人姿态进行实时估计，实现惯性测量单元(IMU)姿态信息与RF2O数据的融合,达到降低系统误差的目的。文中主要研究了机器人末端与复杂环境存在实时接触力情况下，针对现有的阻抗控制在力信号采集过程中存在反馈偏差较大的问题，通过卡尔曼滤波器对返回的力信号进行处理，提高系统的精确性与鲁棒性。

1 机器人与环境接触动力学模型

机器人动力学是机器人进行跟踪控制研究的基础，合适的动力学模型能够帮助机器人更加准确、快速地完成作业任务。当机器人末端与外部环境接触时，机器人的关节空间的动力学表达式为[3]

(1)

其中：qRn为n自由度机器人的关节位移；为机器人的关节角速度；M(q)为n×n维的惯性矩阵；表示机器人的离心力、哥氏力矩阵；G(q)为机器人的关节连杆重力向量；τ为机器人的各轴输出力矩；τe为机器人末端与环境的接触力/力矩。

关节角速度与机器人末端速度关系可表示为

(2)

其中Jq(q)为机器人的雅可比矩阵，表示机器人末端位移与各关节位移之间的关系式。机器人末端位移的加速度为

(3)

则机器人末端速度、加速度与机器人雅可比矩阵的关系为：

(4)

(5)

由上述推导过程式(1)、式(4)、式(5)可以得到机器人与环境接触时的动力学方程为

(6)

2 卡尔曼滤波器模型

针对机器人传感器在返回数据时产生的噪声干扰，文中采用卡尔曼滤波器估计控制过程中机器人状态，预测下一时刻状态，使运动过程中的估计均方差最小，且卡尔曼滤波器在轨迹预测方向有较好的应用[4-9]，不需要对机器人各种误差进行精确的数学建模便可估计期望动作。

卡尔曼滤波器的第一个公式为状态预测公式

(7)

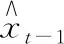
(8)

第三个公式为

Zt=H·xt+v

(9)

其中：H为观测矩阵；v是观测误差；Zt为当前时刻的观测值。

系统状态更新的公式为

(10)

(11)

最佳估计值的噪声分布为

(12)

图1 基于卡尔曼滤波的力控制

(13)

控制模型内的状态方程为

(14)

其中：y(t)为系统输出，是机器人末端与外部相互作用力；wr、wo为系统噪声，和观测噪声均认为是符合期望为u=0,方差σ2分别为Q、R正态分布；x(t)=[x1(t)x2(t)]T；A=[0Kd]T；B=[0 1； 0 -Kv]T；系统分量x1(t)、x2(t)为机器人的受力情况与力相对于时间的一阶导数；系统的输入是u(t-Td)，为系统速度。

3 仿真实验

3.1 力控制模块

通过MATLAB软件中的Simulink来搭建机器人力控制模块[10-12]，控制模型如图2所示，给定期望接触力为Fd=16.75N，环境刚度ke=3000N/m，Md=20,Bd=600,系统响应时间Td=0.001s，观测状态协方差矩阵协方差Rk=0.001 5，系统测量噪声矩阵型方差Qk=0.002，采样时间T=10Td=0.01s，假设力传感器的测量噪声符合随机。

图2 机器人力控制模块

得到经典阻抗控制与基于卡尔曼滤波的力控制仿真的力跟踪结果如图3所示。由图3可以得知基于卡尔曼滤波的力控制可以有效地降低噪声，将力控制在期望值附近，与经典阻抗力控制相比，卡尔曼滤波器有较强的鲁棒性可实现预测和抑制噪声。

图3 力控制结果对比

3.2 可视化仿真

采用某公司KR60系列L45 HA 机器人作为仿真对象，结合MATLAB中的Simscape Multibody工具箱与Simulink中的控制模块可以实现机械系统的可视化仿真，利用基于卡尔曼滤波的力控制模型对目标工件进行外轮廓轨迹跟踪仿真，并与经典阻抗控制模型进行比对，机器人末端力采集位置为力传感器的形心，如图4所示。图中机械臂末端坐标系即为力采集位置的坐标系。

图4 力采集位置

1)平面轨迹跟踪实验

设定目标工件的刚度ke=500N/m，期望力0N，采样时间T=0.01s，卡尔曼滤波的阻抗控制中各参数观测状态协方差矩阵协方差Rk=0.001 5，系统测量噪声矩阵型方差Qk=0.002，力采集的噪声在区间(-10N,20N)内均匀分布，在力采集坐标系中z轴两组仿真结果如图5、图6所示。

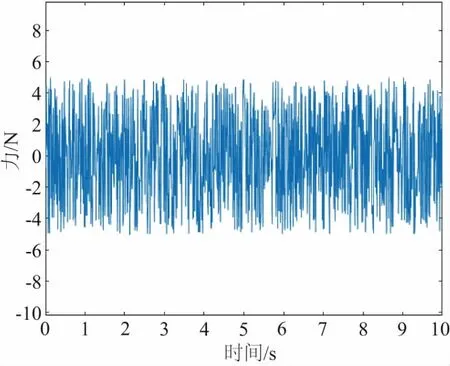
图5 经典阻抗仿真结果

图6 卡尔曼滤波力控制仿真结果

图5为经典阻抗控制模型的力采集结果，图6为基于卡尔曼滤波的力控制采集结果。从实际的仿真结果中可以看出基于卡尔曼滤波的力控制能够有效降低噪声对力控制的影响且能尽量减小机器人末端与工件的接触力并且能保持位置精确。

2)曲面轨迹跟踪实验

用同样的方法验证机器人的力控制策略在曲面上轨迹跟踪的效果，设定目标工件的刚度ke=600N/m，期望力为F=15N，机器人工具与目标工件的动摩擦因数μ=0.07，采样时间T=0.04s，卡尔曼滤波的阻抗控制中各参数观测状态协方差矩阵协方差Rk=0.003 5，系统测量噪声矩阵型方差Qk=0.01，力采集的噪声在区间(10N,20N)内均匀分布，并在目标工件表面添加凹坑、凸起等表面缺陷。仿真过程如图7所示。