往复密封轴用ZHM气动组合密封圈密封性能仿真分析
2021-08-13沈敏宋梅利张华
沈敏,宋梅利,张华
(南京理工大学 机械工程学院,江苏 南京 210094)
0 引言
随着密封技术的不断提高,气缸工作压力逐渐增大,对密封件性能要求也在提高。密封件由原来简单的O形密封圈(NBR)、V形密封圈(NBR+夹织物),发展至较为复杂的Y形密封圈、V 形密封圈、组合密封圈等密封件[1]。密封圈作为气动产品的关键零部件,其失效不仅会增加维修成本,也将大幅度降低产品的性能和使用寿命,因此研究密封圈的密封性能是非常必要的。
近年来,国内外对于密封圈的密封性能进行了多方面的研究,钟亮等[2]利用Abaqus软件仿真分析了橡胶硬度、往复运动速率、摩擦因数等对O型密封圈组合结构的密封性能影响;BHAUMIK S等[3]研究了不同工作压力、往复运动速度对U型密封圈摩擦力的影响规律,并进行了实验的验证;石勇[4]推导研究了各主要因素对往复式机械密封泄露量的影响;张清奎等[5]基于ANSYS软件仿真分析了防尘密封圈的密封性能及影响因素;崔成梁等[6]利用Abaqus仿真材料硬度、接触面摩擦因数、压缩率和接触面椭圆度以及截面几何参数对桩塞器橡胶密封圈性能的影响。
目前对较为复杂的新型组合密封圈研究较少,本文重点介绍了目前已投入市场且性能优越的一款新型ZHM气动组合密封圈,适用于各种气缸活塞杆,起密封和防尘作用的往复运动密封件,广泛应用在气缸、风动机械以及航空航天等设备上。为了进一步研究ZHM气动组合密封圈的密封可靠性,本文借助ANSYS有限元分析软件,建立密封圈的有限元模型,分析各相关因素对ZHM型密封圈接触应力、Von-mises应力及切应力的影响,以期为ZHM型密封圈在结构设计中的使用效果预判提供参考。
1 密封结构及原理
本文主要研究的是波纹管试验台中的直线运动单元。在直线轴承与外界接触侧通常会使用密封圈进行往复运动密封,常用的V形圈在实际使用过程中气体泄漏量较大,密封性较差,故而重新选用一款较为复杂的ZHM型气动组合密封圈。图1为本文研究的ZHM型气动组合密封圈,这是一款结合了防尘与密封性能的新型密封圈,密封圈槽选用参考上海某公司提供的样品手册,选取尺寸为30mm×38mm×12/8mm丁腈橡胶(NBR)密封圈,即工作状态下密封圈外径D=38mm,内径d=30mm,肩壁高T=8mm,总高H=12mm。

图1 ZHM气动组合密封圈结构示意图
ZHM气动组合密封圈的往复运动工作示意图如图2所示。当密封圈处于预压缩时,低压侧“A”形前唇与高压侧“Y”形后唇同时被压缩。前唇装入密封槽后,接触的表面产生一定的接触压力,起到防尘密封作用,后唇则由预压缩变形而产生接触应力实现密封。在外力作用下对活塞进行往复运动。而密封圈与密封槽配合形成的密封压缩量会直接影响密封效果。密封圈的压缩率S为[7]
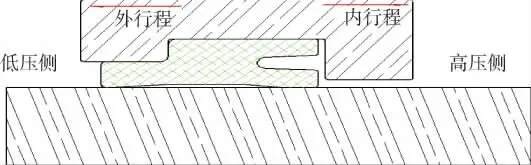
图2 ZHM型气动组合密封圈往复运动工作示意图
式中:b0为ZHM型密封圈压缩前唇边的截面直径或宽度;b为压缩后ZHM型密封圈唇边的截面宽度。
当工作压力作用时,密封圈与密封介质接触的每一点的法相压力均与介质压力的法向压力相等,密封圈根部受到轴向挤压,内外唇受到轴向压缩,密封接触面积变大,接触应力增大。由此知密封结构、工作压力、运动速度、接触面间摩擦系数等都对密封圈密封性能有所影响。ZHM气动组合密封圈的基本工况参数如表1所示。

表1 ZHM气动组合密封圈的基本工况参数
2 密封圈失效准则
要判断ZHM气动组合密封圈能否实现良好的密封,目前普遍是以密封面的接触应力、Von-mises 应力以及切应力3个方面作为失效判据[8]。
2.1 接触应力
ZHM形密封圈的接触应力由预压缩产生的初始接触应力σ0和工作压力产生的接触应力σp组成,表示为
σ=σ0+σp=σ0+kp

根据密封理论与力的平衡原理可知,密封结构确保密封的充分必要条件是接触应力不小于工作介质的内压强,故密封圈的最大接触应力需满足:σ≥p。
2.2 Von-mises应力
Von-mises等效综合应力也叫冯·米塞斯应力,是弹性体疲劳破损失效的主要参考应力。Von-mises应力越大越集中,越易出现裂纹,密封圈发生破损的几率越大。根据第四强度理论,综合等效应力可作为材料失效的判断依据。强度条件为
式中:δm为Von-mises 应力;δ1、δ2、δ3分别为第一、第二、第三主应力;[δ]为材料许用应力。查询机械手册可知本文研究的ZHM型密封圈为丁腈橡胶的材料许用应力为4MPa。
2.3 切应力
切应力是由于载荷等原因致使密封圈受到变形,在密封圈截面产生了相互作用力。当密封圈某处的切应力大于密封圈材料的剪切强度时,该处易被撕裂,导致密封失效。因此,密封圈工作时的切应力应满足
τmax<[τb]
式中:τmax为密封圈工作时所受最大应力;τb为密封圈橡胶材料的剪切强度。橡胶材料的剪切强度可按下式计算:G=2(C10+C01)。其中:C10、C01为Mooney-Rivlin 常数,根据文献[9],C10、C01分别取1.84MPa、0.47MPa,泊松比为0.48,弹性模量E为8MPa。可计算得G=4.68,故本文应满足τmax<4.68MPa。
3 有限元模型
根据有限元原理,本文运用有限元软件 ANSYS 建立丁腈橡胶ZHM形气动组合密封圈有限元分析模型,对其进行密封性能分析。
3.1 密封圈橡胶材料本构模型
橡胶材料的力学模型主要表现为材料非线性、几何非线性和接触非线性。计算大变形下橡胶这类超弹性材料的力学问题,目前普遍采Mooney-Rivlin模型[10]。其应变能密度函数表达式为
U=C10(I1-3)+C01(I2-3)
式中:U为应变能密度;C10、C01为Mooney-Rivlin常数;I1、I2分别为第一、第二格林应变不变量。结合上文可得不可压缩常量d1=(1-2μ)/(C01+C10)=0.009MPa-1。
3.2 基本假设
由于ZHM型气动组合密封圈橡胶材料的特殊性,作出以下基本假设:
1)密封圈材料的弹性模量E和泊松比确定;
2)密封圈受到的纵向压缩视为由约束边界的指定位移引起的;
3)密封圈蠕变过程不引起体积变化。
3.3 仿真模型的建立
根据以上的尺寸在solidwords中建立活塞杆、沟槽和密封圈的二维轴对称有限元分析模型,转换成.xt格式并导入ANSYS中进行有限元分析。建立密封圈在工作中的3个接触对:活塞杆与密封圈之间的滑动接触、密封圈外侧与密封沟槽之间的接触、密封圈端面和密封沟槽端面之间的接触。本文中密封圈是主要研究对象,采用四节点双线性轴对称四边形单元CAX4R对模型进行网格划分,接触单元与目标单元分别采用 CONTA172 和TARGE169。ZHM型密封圈的接触唇等关键接触位置和发生应变比较大的位置进行手动细化网格,以得到更精确的计算分析结果。密封圈总共划分21366个单元,最终划分网格后的有限元几何模型如图3所示。

图3 网格划分结果
往复运动是一个双向过程,主要分为内行程和外行程,其中内行程运动方向与工作压力方向相反,外行程与之相反。密封圈往复运动过程分为预压缩、静密封、动密封3种密封状态。根据这3个过程施加4种载荷步来实现:
1)对活塞杆和密封沟槽施加径向位移,模拟密封圈的压缩量,实现预压缩;
2)由于预压缩和施加压力载荷前后的接触边界几乎不发生变化[11],故可在密封圈迎着压缩气体的表面直接施加压力载荷,实现静密封。
3)密封圈发生位移时,运动过程中速度接近匀速运动,故对活塞杆施加向下位移,模拟外行程运动;
4)对活塞杆施加向上位移,模拟内行程运动。
4 各因素对密封性能的影响
4.1 静密封阶段
ZHM气动组合密封圈安装时为过盈配合,在满足工况条件下,设定密封圈的压缩率为18%,以增加接触面约束,实现预压缩,使得密封圈与沟槽以及活塞杆接触,实现密封,以防止微分方程运算结果不收敛,造成运算错误。再迎着压缩气体的表面直接施加工作压力载荷0.6MPa,实现静密封,静密封的各应力分布云图如图4所示。
从图4(a)可见密封圈最大变形量为1.177 3mm,最大值位于前唇与轴的接触面。从图4(b)知最大接触应力数值为0.868 39MPa,最大值分布于后唇与轴的接触面。这是因为密封圈在受轴向工作压力和径向挤压作用,由于预压缩而发生径向形变,密封圈与轴接触,前后唇与轴和沟槽的接触面受到挤压产生变形,与实际情况相符。图4(c)、图4(d)中可见密封圈等效应力及切应力主要分布于密封圈后唇对称R角处,最大值分别为1.174 7MPa和0.668 84MPa。同时可知ZHM气动组合密封圈的各应力最大值均发生在后唇部位,由此可判断,后唇主要起密封作用。同时后唇对称R角处易发生破坏,要着重注意后唇对称R角处的应力变化,防止应力过大而使密封圈发生破坏。

图4 ZHM气动组合密封圈静密封仿真结果
4.2 往复运动阶段
为了研究ZHM气动组合密封圈往复运动中的密封特性,取其中工作压力P=0.6MPa,摩擦系数f=0.05,运动速度v=200mm/s,压缩率为18%,采用控制变量法,在工况允许范围内,各改变其中一个因素来研究其对最大接触应力、最大Von-mises应力、最大切应力的影响。
1)预压缩量
无论是静密封还是动密封,预压缩率的选择通常会给密封圈的寿命以及密封效果带来很大的影响。对于往复式密封装置,动密封时密封圈的常规压缩率范围为10%~20%[12],改变初始压缩率,观察ZHM气动组合密封圈分别在10%、12%、14%、16%、18%、20%压缩率条件下最大接触压力、最大等效应力和切应力变化情况,关系曲线如图5所示。
可见内外行程各应力的变化趋势是一致的,说明运动方向的改变不受预压缩量的变化的影响。图5(b)、图5(c)中可见内外行程的最大Von-mises应力和最大切应力均随压缩率的增加而减小,最大Von-mises应力减小了约25%,最大切应力减小了约26%,但内行程的最大Von-mises应力及最大切应力始终略大于外行程。其主要原因是工作压力的方向与外行程方向相反,符合实际情况。图5(a)显示内外行程的最大接触应力变化趋势也是相似,当压缩率低于18%时均呈下降趋势,高于18%时出现波动,陡然增长,说明压缩率太大,会造成密封圈的应力松弛,弹性降低,减少密封圈的使用寿命,进而可能导致失去密封的能力。因此在允许的使用条件下,应设法降低压缩率。

图5 压缩率对各应力影响
2)摩擦系数
橡胶产品在成型过程中极易致使橡胶材料大分子链沿某方向形成局部取向,同时由于模具和成型收缩率的差异性,密封圈的表面粗糙程度也会产生差异。因此不同的摩擦系数也可能是影响密封性能的影响因素。密封圈在f=0.05~0.25条件下对最大接触压力、最大Von-mises应力和切应力的影响关系曲线如图6所示。
从图6(a)可看出内行程的最大接触应力随摩擦系数的增大而增加了约26%,当f≥0.15时,增长趋势更明显;外行程的最大接触应力变化趋势和内行程类似,只是当f≥0.1时,增长趋势更明显,而其随摩擦系数的增大而增加了约31%,说明外行程受摩擦系数的影响更大。图6(b)中可看出内行程最大 Von-mises 应力在0.05~0.15之间有微小波动,呈先增大再减小的趋势,当f≥0.15时缓慢增长,整体增长3%,说明内行程受摩擦系数的影响较小;外行程增长速度大于内行程,随摩擦系数的增大而增加了约18%,说明外行程中的最大Von-mises 应力和最大切应力对摩擦系数更为敏感。图6(c)可见最大切应力的内外行程的变化趋势和最大 Von-mises 应力相似,外行程的最大切应力受摩擦系数的影响大于内行程,同时摩擦系数在0~0.25内未超过材料的许用剪切强度,因此不会发生剪切破坏。

图6 摩擦系数对各应力的影响
3)工作压力
ZHM气动组合密封圈在往复运动中的最大工作压力为1MPa,因此取工作压力分别为 0.2、0.4、0.6、0.8、1MPa,分析其对往复密封性能的影响。工作压力对各应力影响的关系曲线如图7所示。

图7 工作压力对各应力影响
由图7(a)可知,内行程的最大接触应力随工作压力的增加而增加了约2倍,外行程增加了约1.7倍,且内外行程的最大接触应力差值从0.05MPa增加至0.12MPa。差值随工作压力的增大而增大,说明随工作压力的增大,内外行程的最大接触应力相差越大。但在这一过程中接触压力始终大于工作压力,满足密封要求。由图7(b)可知,内外行程的最大Von-mises 应力以及最大切应力均随工作压力的增加而增加了约1.7倍,内外行程的变化趋势相同,且内行程始终略大于外行程。其主要原因是工作压力的方向与外行程方向相反,符合实际情况。但同时应力过大也会说明密封圈产生松弛失效现象,因此在实际工作情况下,应保证密封圈在工况允许的工作压力范围内使用,避免ZHM型圈的快速磨损。
4)往复运动速度
往复运动速度是影响动密封的重要因素之一,图8分别给出了往复运动过程活塞杆速度v=0.1~0.5 m/s 时ZHM形密封圈的最大接触应力、最大Von-mises应力及密封面最大切应力对运动速度变化的曲线。

图8 速度对各应力影响
图8显示在外行程过程中,密封圈的最大Von-mises 应力随运动速度的增大而几乎不变、最大切应力随运动速度的增大而基本不变,最大接触应力随运动速度的增大而出现微小波动,说明外行程过程中,速度对密封圈应力影响较小。在内行程过程中,最大接触应力随着速度的增大而增大约38%,说明内行程相较外行程对速度的敏感度更大。最大Von-mises 应力和最大切应力整体随速度的增加而减小的趋势,说明速度较大时,密封圈与沟槽接触面可能变小,易产生间隙导致密封失效。速度在200~400mm/s之间应力几乎未变,说明ZHM气动组合密封圈在此区间能稳定使用。
5 结语
本文采用有限元方法分析了压缩率、摩擦系数、工作压力以及往复运动速度对ZHM型气动组合密封圈密封性能的影响,得出以下结论。
1)往复动密封中,为了保证ZHM型气动组合密封圈的使用寿命和启动性能,不宜取过大的预压缩率以及工作压力。本文分析压缩率在12%~18%之间各应力变化较为稳定。ZHM型气动组合密封圈的材料许用应力在4MPa左右,最大 Von-mises应力以及最大切应力也不能过小,故建议工作压力控制在0.4~0.8MPa左右。
2)往复运动密封中,ZHM气动组合密封圈的切应力及Von-mises应力受摩擦系数的影响较小,接触应力随摩擦系数的增大而逐渐增大;在内行程中,速度对密封圈的各应力影响显著,而外行程受速度的影响较小。
3)往复运动密封中,ZHM气动组合密封圈内行程的切应力及Von-mises 应力均大于内行程,说明内行程更易引起疲劳与剪切破坏。
