基于Deform-3D轴向振动钻削P20有限元仿真
2021-08-13张卫锋张灿祥刘致君吴志强
张卫锋,张灿祥,刘致君,吴志强
(青岛科技大学 机电工程学院,山东 青岛 266061)
0 引言
在模具行业中,P20模具钢凭借其硬度均匀、良好的抛光和光蚀刻花以及其物理特性组织致密等性能,广泛应用于热塑性塑胶注塑模具上。而模具常用的连接方法是用螺丝紧固和销钉定位,因此,需要大量的连接孔。传统的钻削加工有轴向力大、表面质量差、刀具磨损严重等问题。
为解决以上问题,在20世纪五六十年代日本限部淳一郎教授最早提出在刀具上加入振动的理论,并进行了试验验证,另外,他还提出了在传统的机加工方式中加上振动,有利于改善加工工艺性;在国内,华中理工大学熊烽等人研制了使用动态采集的方法分析轴向力和转矩;吉林工业大学王立平等人通过理论分析了低频振动可以消除出口毛刺的作用,并对比了普通钻削,另外,分析了低频振动钻削中钻头寿命和横向偏移机理,得出振动钻削定位精度较高,偏移被消除[1-4]。
本文采用Deform-3D有限元分析软件研究在钻削P20模具钢的过程中,钻削参数对轴向力和转矩的影响规律。
1 轴向振动钻削有限元模型
对于Deform-3D有限元分析软件来说[5-6],其结构是由前处理器、模拟处理器、后处理器3大模块组成。具体的分析步骤如图1所示。

图1 Deform-3D仿真分析步骤图
本文中将涉及到大量的仿真试验,其有限元模型的建立过程基本类似,所以,本节将通过试验设计其中的某一组参数,详细地叙述轴向振动钻削有限元模型的建立过程:以φ5mm的两刃麻花钻、工件直径φ10mm、厚度1.5mm、进给速度0.15mm/r、旋转速度1200r/min、振幅20μm、频率100Hz为示例,建立有限元模型。
1.1 工件及麻花钻模型建立与网格划分
在Deform-3D工具模块中,创建麻花钻实体模型,选择的钻头直径为φ5mm的两刃麻花钻,定义钻头为刚性体即可。另外,工件模型直接输入直径φ10mm、厚度1.5mm即可生成模型,定义工件为塑性体。在网格划分设置中[7-8],工件网格的划分采用绝对网格划分类型,最大网格尺寸和最小网格尺寸的比例设为6,最小单元边长为0.05。麻花钻网格的划分采用相对网格划分类型,定义刀具20000个元素的网格,最大网格尺寸和最小网格尺寸的比例设为4。如图2所示。

图2 麻花钻模型图
1.2 材料定义
定义麻花钻材料为WC(硬质合金),不添加镀层。对于工件材料来说,在钻削过程中大应变、高应变率和高温升的情况是经常发生的[9-10]。因此,通常使用的材料本构关系为J-C模型,其函数关系如式(1)所示,特征参数如表1所示。

表1 P20的J-C特征参数
(1)

1.3 工件接触以及摩擦定义
首先,固定工件侧面所有节点的速度,并为所有表面分配热交换边界条件,工件处于完全固定的状态。此外,在接触设置中,建立钻头与工件的接触关系:钻头自动定义为主要对象,工件自动定义为从属对象,摩擦类型为剪切摩擦,摩擦系数选用恒定摩擦,输入0.6即可;另外,在钻削过程中,切屑可能会接触到工件,所以要创建一个工件与工件之间的自接触。
1.4 工具运动及其他参数设置
在轴向振动钻削中,通过对刀具施加参数配置,以此来实现转动、进给以及振动的运动。在工具运动设置选项内,设置工具沿着z的负方向进给,并绕z轴旋转,角速度必须以弧度/秒为单位定义。
振动钻削的速度是一个周期性的函数[7],即由位移-时间函数式(2)进行求导,得出速度-时间的关系为式(3)。
Z=frNT+Asin(2πfT)
(2)
v=frN+2πfAcos(2πfT)
(3)
本次仿真的参数采用:fr=0.15mm/r;N=1200r/min(即N=20r/s);f=100Hz;A=20μm,代入式(4)得
v=3+12.56cos(200πT)
(4)
由式(4)可知,该振动函数的振动周期为0.01s。对于整个振动钻削过程来说,势必要精确得出工具各个时间点的速度。因此,利用MATLAB软件将时间T定义为T=0∶0.001∶20。然后,进入Deform-3D软件,将MATLAB得出的数据导入其中,就完成了轴向振动钻削工具的进给速度,如图3所示。
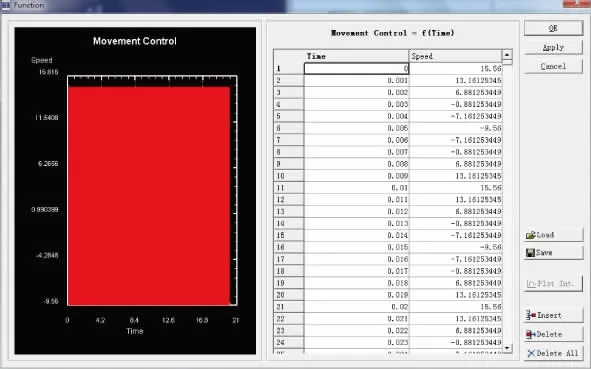
图3 轴向振动钻削工具实时进给速度图
另外,将环境温度、工件和刀具温度统一设定为20℃,热传导系数为45N sec-1·mm-1·℃-1,热对流系数0.02N sec-1·mm-1·℃-1(即为使用空气冷却剂);刀具的磨损模型选择适合于金属切屑的usui模型[10]:
(5)
式中:ω为磨损体积;T为绝对温度;p为压力;V为相对速度;a、b为试验系数,分别取1×10-5和855。
1.5 模拟设定
设置步长为0.001,总模拟步数50000步,每隔25步保存一组数据。另外,设置钻头停止距离为2mm,即为将工件钻透。以上两个条件满足其一仿真即停止[11]。
2 单因素试验设计与分析
2.1 主轴转速对轴向力和转矩的影响
选择相同的进给速度和振幅,并保持其他条件不变,研究主轴转速对轴向力和转矩的影响,设计试验主轴转速从800r/min~1200r/min,试验参数如表2所示。

表2 主轴转速试验参数设计
通过3组不同转速下得到的轴向力和转矩的变化趋势,给出一组代表性曲线如图4所示。可以看出,轴向力和转矩随着参与切削的钻头长度不断增大而从0开始慢慢增大;当钻头的切削刃全部参与切削后,轴向力和转矩到达最大值。而后切削刃保持不变,轴向力和转矩保持稳定,到达稳定切削状态;最后,钻头逐渐钻出工件,轴向力逐渐降低到0,转矩达到稳定值。但是从曲线中可以看出,在某个时刻轴向力和转矩会出现骤变,这是由于切屑的断裂或者是工件网格产生了畸变,软件进行网格重划分所致[10,12-13]。
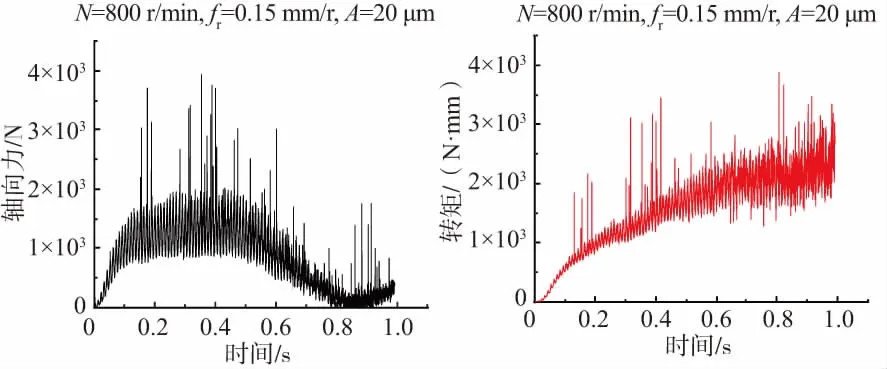
图4 试验1轴向力和转矩的变化趋势
表3为不同转速下轴向力和转矩的试验结果。根据表3绘制出主轴转速对轴向力和转矩的影响趋势,如图5所示。可以看出主轴转速对轴向力和转矩的影响整体上来说并不是很大,只是有微微变化。在对P20模具钢振动钻削过程中,随着主轴转速的提高,工具外侧振动的速度分量在总合成速度中作用减小,速度的动态切削角度的波动减小,导致振动钻削对轴向力的减小作用有所减弱。因此,随着主轴转速的提高,轴向力有所增大;而对于转矩来说,轴向力增大,切向力减小,转矩即为切向力与外侧切削刃到回转中心的距离的乘积[14-15],故随着主轴转速的提高,转矩有所减小。

表3 不同转速下轴向力和转矩的试验结果
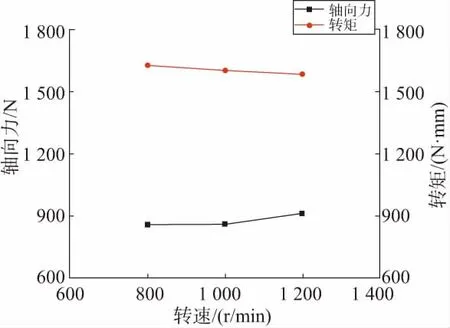
图5 不同转速对轴向力和转矩的影响趋势
2.2 进给速度对轴向力和转矩的影响
选择相同的主轴转速和振幅,并保持其他条件不变,研究进给速度对轴向力和转矩的影响。设计试验进给速度从0.1mm/r~0.2mm/r,试验参数如表4所示。
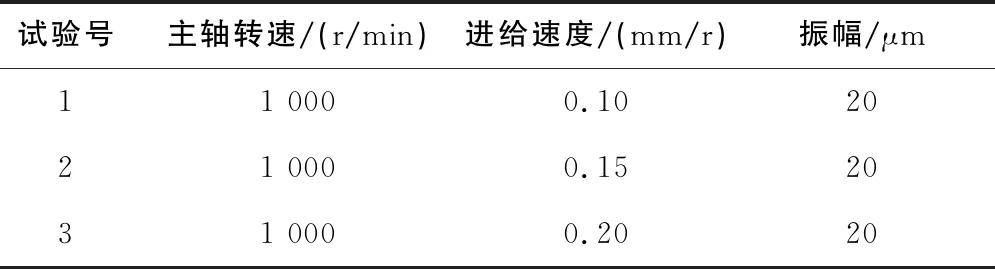
表4 进给速度试验参数设计
通过3组不同进给下得到轴向力和转矩的变化趋势,给出一组代表性曲线如图6所示。其曲线的分析同上。表5为不同进给下轴向力和转矩的试验结果,根据表5绘制出进给速度对轴向力和转矩的影响趋势,如图7所示。从图中可以明显看出进给速度对轴向力和转矩的影响非常大,在对P20模具钢振动钻削过程中,随着进给速度的提高,工具与工件的实际切削面积增大,材料去除率响应增大,刀具每转去除材料所做的功随之增加,进而增大了工具所受轴向力和转矩。

图6 试验2轴向力和转矩的变化趋势
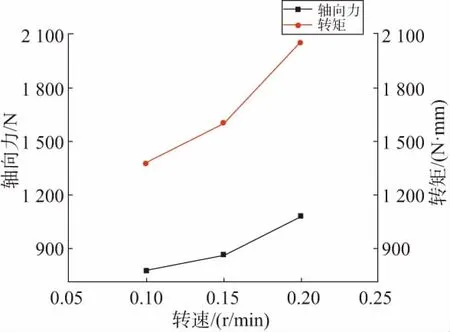
图7 不同进给对轴向力和转矩的影响趋势

表5 不同进给下轴向力和转矩的试验结果
2.3 振幅对轴向力和转矩的影响
选择相同的主轴转速和进给,并保持其他条件不变,研究振幅对轴向力和转矩的影响。设计试验振幅从10μm~30μm,试验参数如表6所示。

表6 振幅试验参数设计
通过3组不同振幅下得到的轴向力和转矩的变化趋势,给出一组代表性曲线如图8所示,其曲线的分析同上。表7为不同振幅下轴向力和转矩的试验结果,根据表7绘制出振幅对轴向力和转矩的影响趋势,如图9所示。随着振幅的增大,工具所受的轴向力和转矩都呈现降低的趋势,这是由于振幅的提高使得材料塑性变形的抗力减小,进而使得轴向力和转矩同时减小。

图8 试验3轴向力和转矩的变化趋势
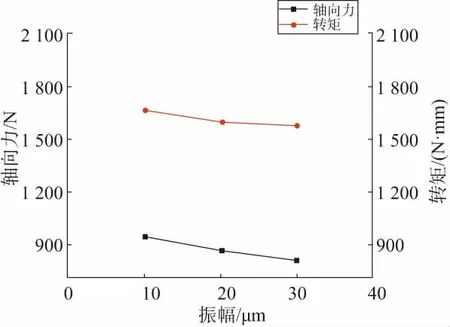
图9 不同振幅对轴向力和转矩的影响趋势

表7 不同振幅下轴向力和转矩的试验结果
2.4 与普通钻削的对比试验
选择相同的主轴转速和进给,并保持其他条件不变,对比普通钻削与振动钻削,设计试验参数如表8所示。
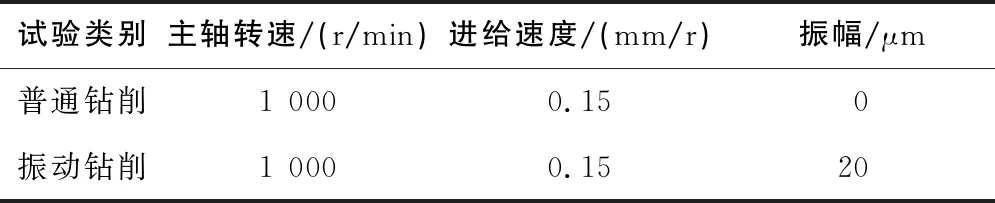
表8 普通钻削与振动钻削的对比试验参数设计
图10为仿真所得的分别用振动钻削和普通钻削两种不同加工方式下钻削P20模具钢的轴向力和转矩的变化曲线,通过观察图10的曲线变化,可以看出由于普通钻削是工具与工件之间连续接触、挤压以及切削,使得轴向力和转矩的变化曲线是连续的;而振动钻削得到的轴向力和转矩曲线是以周期性变化的。这是因为工具与工件的周期性分离,由原始的连续切削变成了冲击接触,其钻削条件得到改善。关于曲线的其他分析同上,在此不作过多描述。

图10 不同加工方式下轴向力和转矩的变化趋势
表9为不同加工方式下轴向力和转矩的试验结果,根据表9绘制不同加工方式对轴向力和转矩的影响趋势,如图11所示。从图中可以明显看出,相对于普通钻削加工,轴向振动钻削的轴向力和转矩均有所下降。图14中普通钻削P20的平均轴向力和转矩分别为962.0N、1 661.2N·mm,而在频率为100Hz的轴向振动钻削P20的平均轴向力和转矩分别为860.1N、1 601.4N·mm。因此,与普通钻削相比,在低频的轴向振动钻削中,已经使得平均轴向力和转矩分别下降了11%和4%。所以,相较于普通钻削加工来说,轴向振动钻削可有效减小轴向力和转矩,进而提高材料去除率。

表9 不同加工方式下轴向力和转矩的试验结果

图11 不同加工方式下轴向力和转矩的影响趋势
3 正交试验设计与分析
3.1 试验设计
在轴向振动钻削过程中,合理地选择钻削参数对提高加工质量和效率将起到很大的作用。因此本小节采用正交试验法仿真研究主轴转速、进给和振幅对轴向力以及转矩的影响,以此来验证单因素试验的结论,并通过计算极差值找出影响最大的因素。表10为正交试验的因素水平表,表中因素数为3,水平数为3,属于等水平正交表,选择最接近的正交表为L9(34),建立表11正交试验的安排。
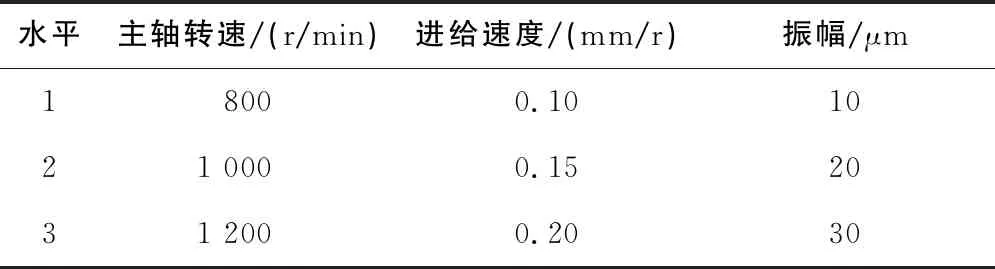
表10 因素水平表

表11 正交试验因素安排
3.2 试验结果及分析
通过9组正交试验得出的轴向力和转矩的整体变化趋势,现给出3组代表性曲线如图12所示,整理其数据得出平均轴向力和转矩的正交试验结果,如表12所示,对其结果进行极差计算,得出表13。其中,进给速度的极差值最大,说明在轴向振动钻削P20过程中,进给速度是影响轴向力和转矩最主要的因素。各影响因素的影响程度的排序依次为:进给速度>振幅>主轴转速。
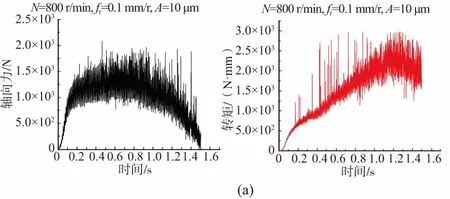
图12 不同钻削参数下部分试验轴向力和转矩的变化趋势
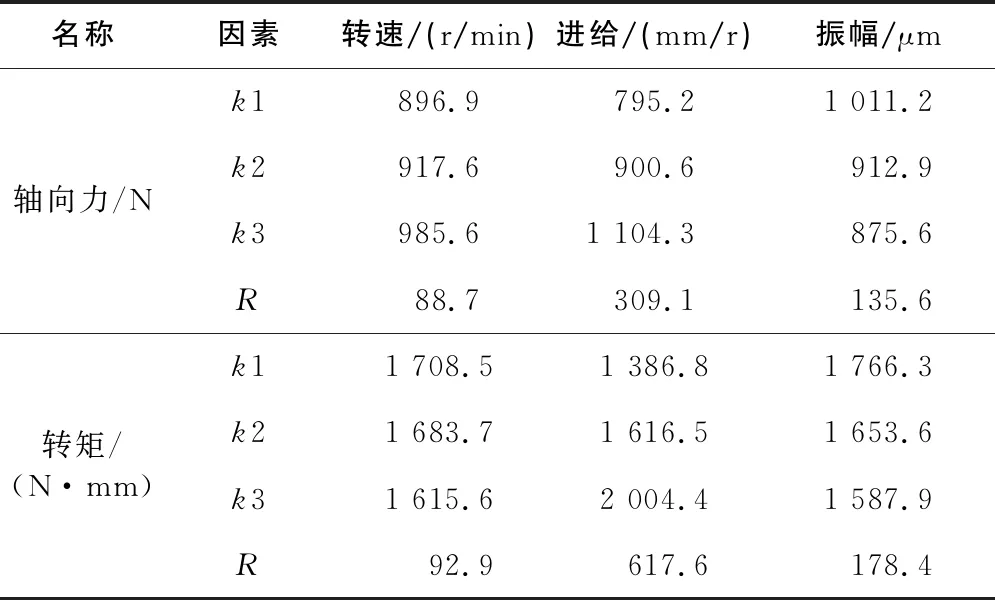
表12 正交试验极差分析

表13 正交试验结果
根据极差分析表的均值k,绘制出各因素水平趋势图,如图13所示。主轴转速提高,轴向力呈现缓慢上升的趋势,而转矩呈现缓慢下降的趋势;进给速度提高,轴向力和转矩都呈现急剧上升的趋势;而随着振幅的提高,轴向力和转矩均呈现下降的趋势。其规律与单因素试验规律相同。

图13 振动钻削P20轴向力和转矩因素水平趋势图
4 结语
文章基于Deform-3D软件对P20进行振动钻削仿真模拟,通过研究钻削参数对于钻头轴向力和转矩的影响,得出如下结论:
1)通过单因素和正交试验两种试验方法研究得出轴向力随着主轴转速的增加有微微增大的趋势,转矩有微微减小的趋势;随着进给速度的增大而增大,而轴向力和转矩随着振幅的增大而减小。通过极差值大小可以看出,各影响因素的影响程度的排序依次为:进给速度>振幅>主轴转速。
2)相对于普通钻削加工来说,轴向振动钻削的轴向力和转矩均有所下降。
