某直升机尾传动轴系非线性振动特性的试验研究

倪德，邹亚晨，王平，周煌亮，张根辈，臧朝平

(1. 中国航发湖南动力机械研究所，湖南 株洲 412002； 2. 直升机传动技术国防科技重点实验室，湖南 株洲 412002；3. 南京航空航天大学 能源与动力学院，江苏 南京 210016)

0 引言

尾传动轴系是直升机传动系统的重要组成部分，是一个由多段传动轴、多个联轴器和多个轴承支座连接在一起的复杂系统。它可以连接主减速器和中间减速器以及尾减速器，并传递动力到尾桨，保证直升机的正常飞行[1]。由于受连接方式、支承刚度和结构布局等影响，在复杂工况作用下，尾传动轴系呈现强烈的非线性动力学特征。强非线性系统具有极强的不确定性，在结构设计、仿真、试验阶段都存在一系列不可预测的问题。

目前尾传动轴系的动力学建模和模态试验还主要基于线性理论。倪德等[2]研究了直升机机动飞行时尾传动轴的横向振动建模与特性，基于扩展哈密顿原理，建立了直升机空间机动飞行下尾斜轴横向弯曲振动的动力学模型，分析了直升机空间机动飞行对尾传动轴横向弯曲振动特性的影响。陆凤霞等[3]进一步通过几种典型机动飞行分析了直升机各转动分量对尾传动轴临界转速的影响。许兆棠等[4]分析了直升机尾传动系扭转振动特性。聂峻峰[5]研究了直升机传动轴系结构及动力学特性研究。朱自冰等[6-7]建立了直升机尾传动系统扭转振动的等效多自由度动力学模型，并进一步分析了刚度对直升机尾传动系统弯曲振动固有频率的影响。

近年来，已经发展了多种非线性模态分析理论与方法，并逐渐开始在实际工程领域中应用。KERSCHEN G等[8]系统介绍了结构动力学中的非线性振动试验和参数辨识方法，介绍了各种时域、频域和模态分析方法。GÖGE D等[9]则采用一种模态模型对一个典型非线性结构进行了模态辨识。ARSLAN Z等[10]在大飞机的地面振动试验中，采用线性图示法对大飞机进行了非线性试验模态分析。ZANG C P等[11]则提出了恒位移测试与恒速度测试的基本概念，应用于美国SANDIA国家实验室的非线性结构动力学模型确认挑战问题。ZHANG Genbei等[12-13]则进一步发展了这种方法。杨稀等将恒速度测试方法用于转子系统非线性支承刚度的辨识[14]。CARRELLA A等[15]采用类似的思想，利用标准振动试验获取的频响函数进行某直升机整机结构的非线性试验模态分析。单卫东等[16]在CARRELLA A等的研究基础上，对方法进行了改进，提出了基于频响函数的非线性模态分析方法，并在通过膜片联轴器联接的两根尾传动轴中进行了应用。邹亚晨等[17]进一步应用该方法，识别了两根尾传动轴的非线性连接刚度。

目前关于直升机全尺寸尾传动轴系非线性振动特性的试验研究较少，在工程设计中缺乏试验依据。为此，本文针对某直升机全尺寸的尾传动轴系，通过非线性振动试验，研究了其等效固有频率和阻尼比等振动特性随激励水平的变化规律，为实际工程中直升机尾传动轴系的动力学设计优化提供参考。

1 尾传动轴系的非线性振动试验方法

1.1 结构简介

某直升机全尺寸的尾传动轴系由5段水平轴、1段斜轴组成，轴的材料为铝合金，全长大约20m，如图1所示。轴与轴之间通过膜片联轴器联结，每根轴通过黏性阻尼器支承在基础上，如图2所示。其中膜片联轴器如图3所示，由多层金属膜片组成，会给结构引入复杂的非线性刚度，详细介绍见文献[18]。目前关于其非线性力学特性的试验研究较少，而黏性阻尼器则为结构引入了非线性阻尼力。

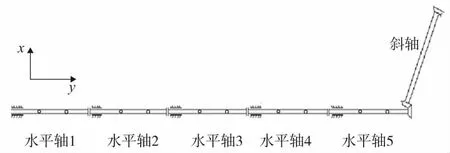
图1 某尾传动轴系的结构示意图

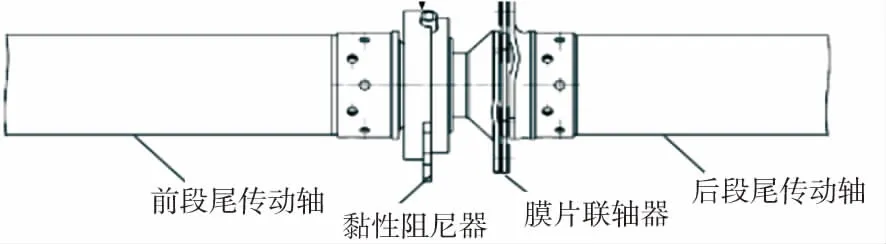
图2 某尾传动轴系连接示意图

图3 膜片联轴器实物

1.2 非线性振动试验方法

某尾传动轴系的非线性振动试验流程如图4所示，主要试验步骤如下：

图4 某尾传动轴系的非线性振动试验流程

1)对尾传动轴系进行不同激励水平下的正弦扫频试验，获取不同激励水平下的加速度频响函数；

2)将不同激励水平下的加速度频响函数转化为位移频响函数，进一步获取位移响应，通过非线性模态分析方法得到等效固有频率随位移水平的变化关系；

3)将不同激励水平下的加速度频响函数转化为速度频响函数，进一步获取速度响应，通过非线性模态分析方法得到等效固有阻尼比随速度水平的变化关系；

4)结合步骤2)和步骤3)，即可辨识尾传动轴系等效线性化的固有频率和阻尼比随着响应水平的变化关系。

1.3 等效固有频率的识别方法

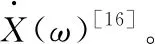
(1)

(2)

X(ω)=Hd×F

(3)

(4)

一般来说，对于位移响应，在共振峰值两侧存在位移幅值相同的两个点，如图5所示。

图5 位移幅值线性化

可以通过一对对称的位移频响函数点来定义位移频响函数的实部和虚部。

(5)

其中频响函数的实部和虚部可以通过频响函数幅值和相位差之间的关系获得。

H=|H|cosφ+j|H|sinφ

(6)

通过联立上面两式，可以得到与位移响应幅值相关的等效固有频率

(7)

在每个激励水平下，通过截取位移响应峰值两端对称的位移频响函数点，即可以建立起固有频率与位移幅值、激励力幅值之间的对应关系。

ωr=f(X,F)

(8)

在每组激励力下，固有频率的变化很小，可以取中间值作为近似值，则公式可以进一步简化为

(9)

1.4 等效阻尼比的识别方法

类似地，对于速度响应，在共振峰值两侧存在速度幅值相同的两个点，如图6所示。

图6 速度幅值线性化

在每个给定速度响应幅值下，可以通过一对对称的速度频响函数来定义速度频响函数的实部和虚部。

(10)

通过联立上面两式，可以得到与速度幅值相关的模态损失因子。

(11)

其中模态损失因子是模态阻尼比两倍的关系。

ηr≈2ξ

(12)

在每个激励水平下，通过截取速度响应峰值两端对称的速度频响函数点，即可以建立起阻尼比与速度幅值、激励力幅值之间的对应关系。

(13)

在每组激励力下，阻尼比的变化很小，可以取中间值作为近似值，则公式可以进一步简化为

(14)

2 某尾传动轴系的非线性振动试验与分析

2.1 尾传动轴系的正弦扫频测试

尾传动轴系非线性振动试验的安装布局如图7所示，一共布置了10个振动测点(安装加速度传感器)，激振器安装于水平轴3的6号测点位置。激振器采用某公司的电动激振器。测试系统采用的是LMS公司24通道的模态测试系统。

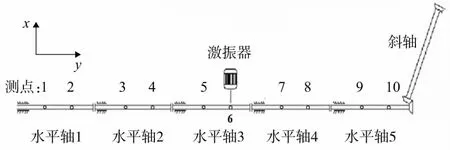
图7 尾传动轴系振动试验的安装布局示意图

对尾传动轴系进行一系列不同激励水平的正弦扫频测试。通过反馈控制，控制激振器的激励幅值分别为0.5N、1N、2N、3N、4N、5N、6N、7N。测试得到的8种不同激励水平下的加速度频响函数的幅值和相位分别如图8和图9所示(本刊系黑白印刷，如有疑问请咨询作者)。可以看出，随着激励水平的增大，频响函数的幅值和相位发生了复杂而有规律性的变化。

图8 不同激励水平下的加速度频响函数的幅值

图9 不同激励水平下的加速度频响函数的相位

2.2 尾传动轴系等效固有频率的识别

采用1.3节所介绍的方法，可以得到8种不同激励力水平下的固有频率随位移幅值的变化关系如图10所示。对于每个激励力水平，固有频率的变化可以忽略不计，每条曲线上的点表示固有频率的平均值，随着激励水平增大，整体呈现增大的趋势。

图10 等效固有频率随位移幅值的变化

不同激励下等效固有频率的平均值如图11中散点所示，可以看出随着位移幅值的增大，等效固有频率增大了将近0.6Hz，约为0.64%，尾传动轴系呈现刚度渐硬的非线性特征。

图11 等效固有频率拟合

进一步对图11中散点进行多项式拟合，可以得到等效固有频率随位移幅值变化的函数表达式(15)，来定量描述等效固有频率随着位移幅值的变化规律，反映尾传动轴系的非线性刚度特性，为其动力学设计优化提供参考。

(15)

需要注意的是，在试验中如果激励水平控制不稳定，重复性试验将产生一定的误差。所以试验中需要对电动激振器的激振力进行反馈控制，确保不同频率下的激励保持恒定，一般可确保误差在可接受范围之内。文献[19]通过两根尾传动轴连接结构，对试验的重复性误差进行了详细分析，本文不再赘述。

2.3 尾传动轴系等效阻尼比的识别

类似地，采用1.4节所介绍的方法，可以得到8种不同激励水平下等效阻尼比随速度幅值的变化关系如图12所示。每条曲线上的点表示阻尼比的平均值。

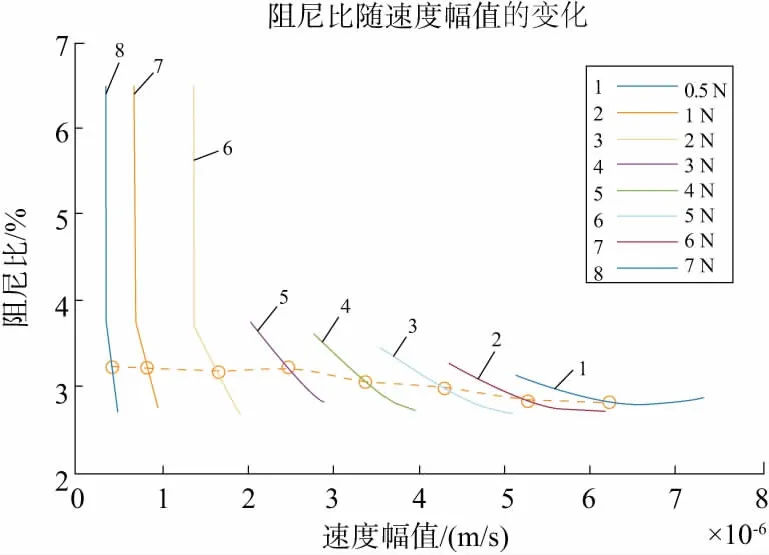
图12 等效阻尼比随速度幅值的变化

将图12中散点标记的平均阻尼比绘图如图13所示，可以反映尾传动轴系的等效阻尼比随速度幅值的变化关系。可以看出，随着激励力水平的增加，速度响应幅值也逐渐增大，而尾传动轴系的阻尼比则减小了12.4%左右。

图13 等效阻尼比拟合

对不同速度幅值下的平均阻尼比进行多项式拟合，可以得到阻尼比随速度幅值的函数表达式(16)，来定量描述等效阻尼比随着速度幅值的变化规律，反映尾传动轴系的非线性阻尼特性。

(16)

3 结语

本文通过非线性振动试验研究了某直升机全尺寸的尾传动轴系的非线性动力学特性，获得了其等效固有频率和阻尼比随激励水平的变化规律，可以为其动力学设计优化提供参考。试验结果表明：

1)随着位移水平的增大，尾传动轴系的等效固有频率逐渐增大，在试验中增加了0.64%，反映了其刚度渐硬的非线性刚度特征；

2)随着速度水平的增大，尾传动轴系的等效阻尼比则逐渐减小，在试验中减小了12.4%，反映了其非线性阻尼特性。

通过这种方法建立的尾传动轴系的等效固有频率和等效阻尼比随着激励水平的变化关系可以进一步为研究尾传动轴系的非线性动力学特性、建立更加精确的非线性动力学模型并进行预测设计提供支撑。