连续曲线钢箱梁荷载试验及有限元分析

朱春凤，艾化学，肖 波，徐 彬，刘 浩，田 伟，金玉杰

（1.吉林建筑大学 土木工程学院，长春 130118；2.长春市市政工程设计研究院，长春 130041）

随着城市交通的快速发展，城市桥梁建设不断向着更轻、更大跨度、更节省材料、更美观方向发展。连续曲线钢箱梁结构的整体性好，在跨中与支点的正、负弯矩能力几乎相等，能节省张拉预应力钢束的烦琐步骤，施工工序也得到了极大的简化，并且钢箱梁截面为闭口空心形式，环状结构有着很好的抗弯、抗扭能力，当材料量一定时，箱型结构可以比其他的截面形式的抗弯、抗扭刚度更大，因此曲线钢箱梁桥在城市立交系统中发挥着极为重要的作用。中外众多学者对曲线连续梁桥进行了研究。Hu 等［1］、Tryland 等进行了钢箱梁的试验研究及有限元分析，研究表明钢箱梁极限承载力的试验实测值与有限元数值结果之间的误差较小。陈海滨［3］利用梁格法对异形钢箱梁桥进行设计与分析。陈博［4］对异形混凝土钢箱梁进行了静力性能研究。卢群［5］运用有限元计算软件建立了箱桥梁的结构分析计算模型，计算了桥梁的设计承载力。罗国庆［6］对连续钢箱梁桥静动载效应计算进行了计算研究。姚亚东等［7］、罗鸿等［8］对大跨度箱梁桥进行了有限元及试验研究，得出在计算荷载作用下，结构应力水平较低的结论。李青等［9］对组合箱梁桥承载能力进行了试验研究，得出桥梁的极限承载力。刘斌［10］分析了曲线钢箱连续梁桥极限承载能力，得出该结构承载能力高等的特点。本文依托实际工程，对连续曲线钢箱梁桥进行静荷载与动荷载试验的试验概况、试验检测过程和结果进行介绍，基于试验结果进行受力状态分析，结合有限元理论进行承载力及变形计算分析，得出连续曲线钢箱梁桥的承载力及变形，以期为今后此桥梁建设提供有效的理论基础。

1 工程概况

依托吉林省某快速路系统工程中变截面连续钢箱梁桥进行研究。桥梁全长210 m，跨径为65+80+65 m，桥宽25 m，双向六车道。边支点梁高3 m，中支点梁高5 m。双柱式花瓶墩，摩擦桩基础。横断布置：0.5 m（桥侧护栏）+11.75 m（车行道）+0.5 m（中央护栏）+11.75 m（车行道）+0.5 m（桥侧护栏）=25 m，桥面双向1.5%横坡，荷载等级为公路I 级，钢材等级为Q345qE。

2 有限元模型

有限元模型如图1所示，共2 056个节点和3 660 个单元。

图1 MIDAS 全桥模型

3 静力荷载试验

3.1 试验项目

静力荷载试验主要包括以下两方面：1）主梁正弯矩控制截面应变及挠度检测。2）支点负弯矩控制截面应变检测。

3.2 试验工况

加载车辆为40 t，分级加载，分为5 种工况，见表1。数据只给出有代表性的前3 种进行对比分析。

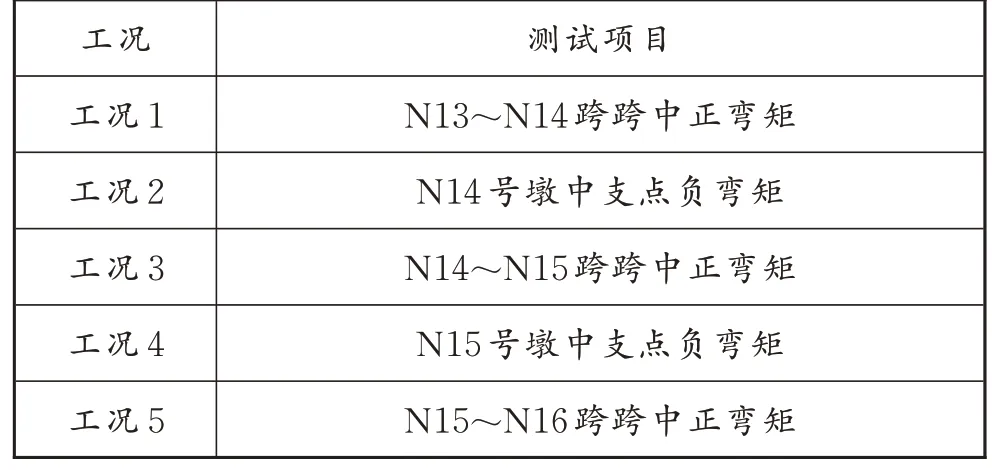
表1 静力荷载试验工况

3.3 测点布置

连续曲线钢箱梁各截面的位移测试点为每跨支点、四分点和跨中处，应变测试点为跨中和两个中支点的位置，具体位置如图2 所示。

图2 连续箱梁主桥位移和应变测试点布置

采用型号为JMZX-212 振弦式应变计进行测量，采用数显百分表测量挠度。试验前和试验过程中需要对每个观测截面的部位裂缝情况通过裂缝测宽仪观测其宽度及变化。测试结果见表2。

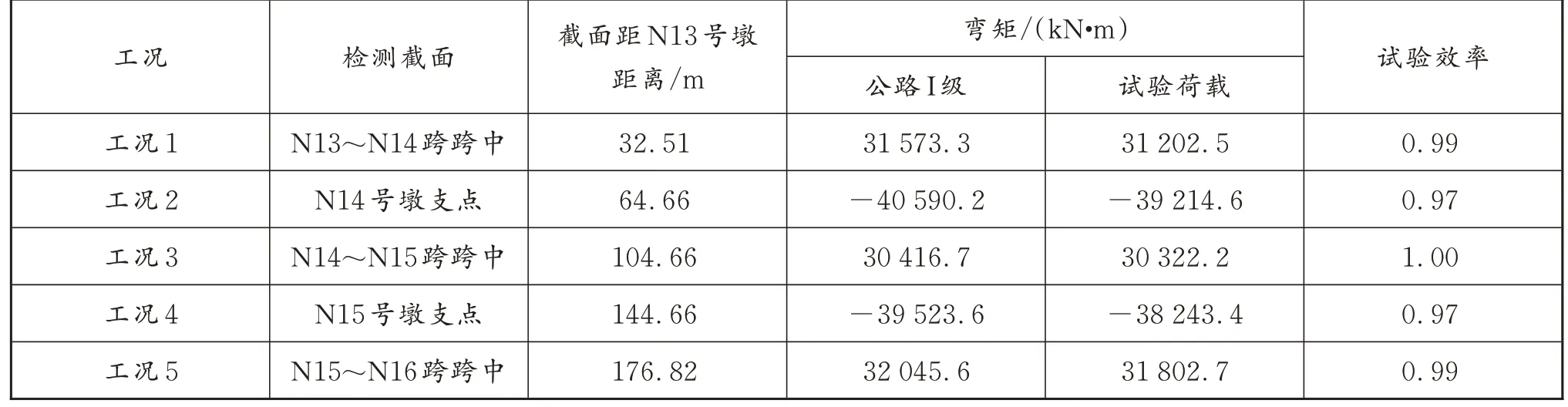
表2 静载试验荷载效率测试结果

3.4 静载试验结果及分析

3.4.1 挠度测试结果

根据实际测试结果，在所划分的三至四级划分中，均为最后一级结果的荷载效率最大。因此这里只列出在最后一级荷载作用下不同工况的试验结果，分别见表3～表5，计算值与试验值对比如图3 所示。

表3 工况1 各测点竖向位移（挠度）计算结果和试验结果对比

表5 工况3 各测点竖向位移（挠度）计算结果和试验结果对比

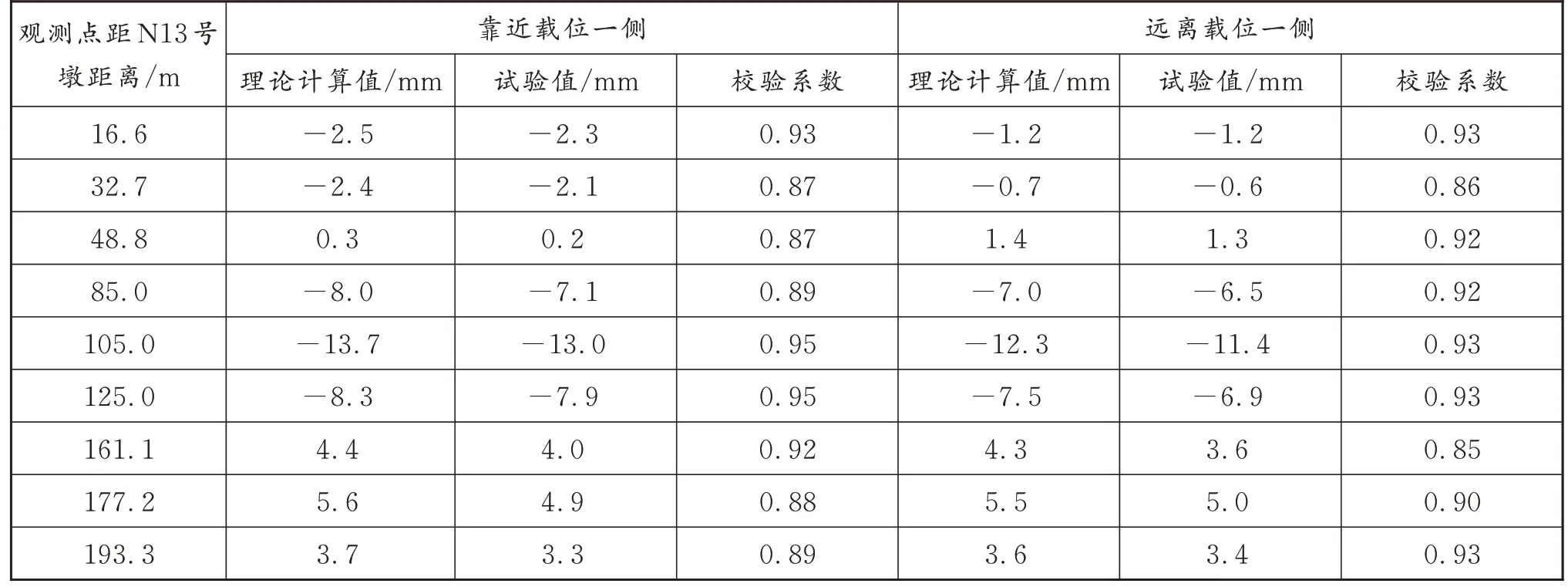
表4 工况2 各测点竖向位移（挠度）计算结果和试验结果对比

各测点在卸除荷载后，其最大相对残余变形量为8%，桥梁检测规范所规定的极限值为20%，该桥没有超过这一限定，其现阶段工作状态可近似认定为弹性工作，并且图3 表现出荷载与其作用下所产生的挠度具有很好的相关性，从表3～表5 可以查得挠度的校验系数最大为0.95。试验荷载作用下的测试结果均小于理论计算结果，也说明该桥的竖向刚度满足使用要求。

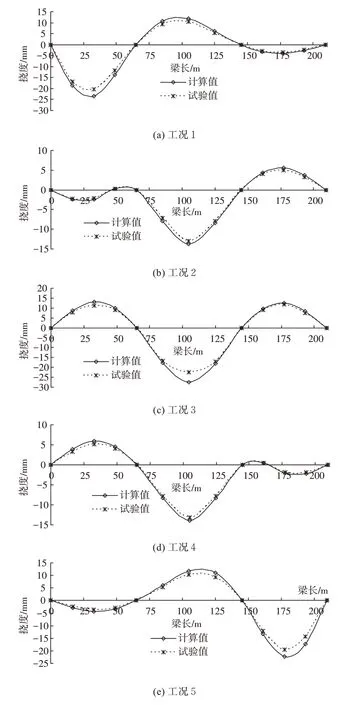
图3 各工况条件下测点计算值与试验值对比

3.4.2 应变测试结果

同挠度测试结果相同，只列出在最后一级荷载作用下不同工况的试验结果，分别见表6～表8。表中第1 跨、第2 跨和第3 跨分别代表N13～N14 跨、N14～N15 跨和N15～N16 跨，中支点1、中支点2 则代表N14 号墩、N15 号墩处支点。

表6 工况1 各测点竖向应变计算结果和试验结果对比

表7 工况2 各测点竖向应变计算结果和试验结果对比

表8 工况3 各测点竖向应变计算结果和试验结果对比

经过分析各点应变的理论和实测值，能够计算各点的残余应变量，卸载后的最大残余应变相对量为13%，满足规范要求，应变校验系数最大为0.88，证明该桥在发生形变后恢复原始形状的能力较强。

经过5 个工况的车辆荷载计算后，对桥梁的内力、应力和位移的实际测量与理论结果对比分析可知：

1）施加公路I级荷载后，最大正弯矩为6.522 7×103 kN·m，位于第3 跨跨中位置，第1 跨为曲线钢箱梁，受曲率半径和材料属性的影响，其最大正弯矩稍小于第3跨的最大正弯矩，而最大负弯矩为8.267 2×103 kN·m，位于N15 号墩支座处。

2）从N14 号墩和N15 号墩的剪力影响线可以得出第1 跨能引起最大正弯矩的影响线范围要远大于第3 跨。

3）在各种静力工况下，钢箱梁的最大正应力为29.02 MPa，最小正应力为-13.61 MPa，均未超过设计值，最大应力的变化规律与弯矩的变化规律大致是一致的；钢箱梁的最大剪应力为9.12 MPa，最小剪应力为-9.93 MPa；在各种静力工况下，钢箱梁的挠度最大值为22.90 mm。

4）经过静力荷载试验所获得数据的分析，不同工况下的挠度和应变的实测值、理论值所计算的校验系数均小于规范规定的限值，表明桥梁的竖向承载能力满足使用的要求，并且挠度也小于L/600 的要求。相对残余应变和变形量小于20%，也表明钢箱梁比预应力混凝土箱梁恢复能力更佳。

4 动力荷载试验

4.1 动力试验实施方案

本次试验主要测定结构的振动特性，包括结构自振频率的测定及结构自振阻尼比的测定，在桥面无任何外界振源激励的前提下，通过动力测试系统来测定因随机荷载激振引起桥梁结构微小振动的响应，测得桥梁结构的自振频率及振型等动力学特征。结构自振特性计算结果见表9；主桥结构前两阶振型如图4 所示。

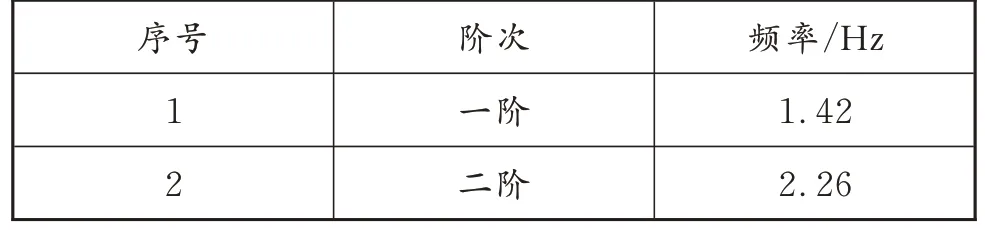
表9 桥梁自振频率

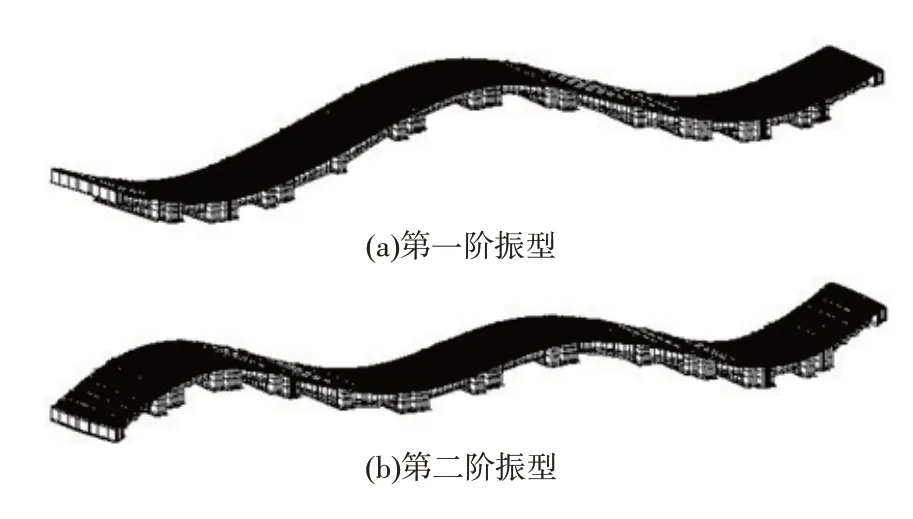
图4 结构前两阶振型

4.2 试验结果及分析

实测频率及阻尼比见表10。

表10 模态试验分析结果

通过对连续钢箱梁桥进行环境激励试验以后，采用模态分析方法，通过加速度信号的处理生成频响函数，从加速度响应力学指标中分析出桥梁结构的动力特性基本参数。模态计算值与试验测试值的比较见表11。根据实测动力参数，对桥梁的动力使用性能进行评价。

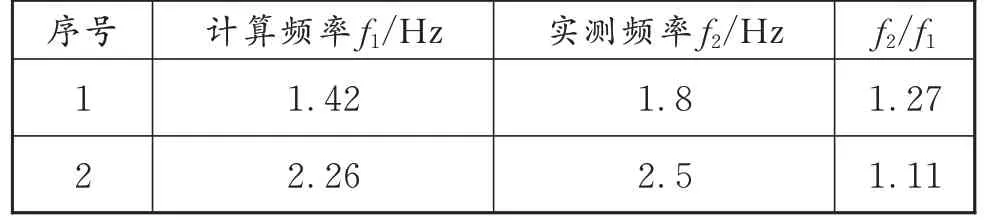
表11 模态计算与试验值比较

频率测试结果表明，桥跨检测动刚度满足设计要求。阻尼比实测结果表明，桥跨检测整体工作性能较好，具有一定的耗能能力。

综上，桥跨检测的动力使用性能满足设计要求。

5 结论

通过对连续钢箱梁桥进行静动载试验及计算分析，得出以下结论：

1）根据连续钢箱梁的静力计算及测试数据，曲线梁段的最大弯矩值小于直梁段，剪力影响线范围大于直梁段。

2）连续钢箱梁的静力理论计算值和实测值符合较好，各项指标均在规范限值容许范围之内，且钢箱梁变形恢复能力比预应力混凝土箱梁更佳。

3）动载试验结果表明，钢箱梁桥跨动刚度满足设计要求，具有一定的耗能能力，桥跨检测的动力使用性能满足设计要求。