基于改进的节点贴近度簇划分算法的研究

李慧 许英

摘 要：复杂网络中社区结构的发现是数据挖掘领域的研究热点，也是进一步发现社区关系知识的前提。根据网络的系统局部信息和全局信息，计算通过网络系统节点之间的贴近度矩阵，并将网络节点可以按照贴近度和模块度指标划分为两个不同的簇。在四个实际网络数据集以及计算机生成网络的实验结果表明，该算法相比Newman、GN等[1]算法具有更高的准确率。

关键词：复杂网络;节点贴近度;簇划分;簇结构

中图分类号：N94;TP393  文献标识码：A  文章编号：1673-260X（2021）06-0023-05

引言

在不同的域中，许多类型的数据可以用网络来表示，其中节点代表个体，节点之间的边代表个体之间的关系。在社会网络中，信息的传递、人与人之间的交流以及蛋白质结构的作用可以帮助我们通过将这些问题构建复杂的网络来分析。因此，复杂网络起着重要的作用，而社区划分是研究复杂网络结构和功能特征的最基础的工作。多年来对于复杂网路的簇划分进行了广泛的研究，如GN（Girvan-Newman）算法[1]、谱划分算法[2]、层次聚类算法[3]、标签传播算法（Label Propagation Algorithm，LPA）[4，5]、密度分值聚类算法[6]等。GN算法的基本理论思想是从网络中删除信息中介度最高的边，直到没有边，每个时间节点是一个国家独立的簇。谱方法是基于图的Pierre-Simon Laplace矩阵，标签传播算法是一种适用于大规模复杂网络的线性社区划分方法，使用不同的标签来识别不同的社区;文献中的密度峰值算法结合了Jaccard指数和最短路径信息，形成复合贴近度[6]。然后，通过改进的密度峰值模型计算每个节点的密度和最小距离，并在关键节点列表中选择密度最高、距离最短的节点。此外阈值条件使密度峰模型分析能够更加准确地选择一个具有一定代表性的关键节点。社区聚类的内容包括非关键节点的分配、社区的合并和不稳定节点的属性修改。

社区进行划分的基本理论思想是将具有非常贴近属性的节点划分为同一个领域。因此，本文主要研究基于局部贴近度的算法，构造节点贴近度矩阵（Modified Similarity Matrix，MSN）MSN={Sij}，Sij表示节点i和j的贴近性程度。根据贴近度矩阵对社区进行初步划分。

1 节点贴近度

计算节点贴近度方法主要分为基于全局和基于局部信息这两类，比如Jaccard[7]，AA，PA[8]，RA[9]，HPI[10]，CRA，CPA等贴近度指标，RA指数是构造节点贴近度的最有效方法[10]。

RA方法通过模拟网络中的资源分配过程来测量两个节点的贴近性。对于任何一个网络，都不能看作是一些重要节点和一些边组成的图。定义图G=（V，E），其中V是顶点集，E是边集。顶点数n=|V|，边数k=|E|。假设图G（V，E）中节点对（i，j）通过它们共同的邻居进行通信，两个节点的亲密程度取决于它们共同邻居的程度。将节点i和节点j之间的贴近度定义为贴近度，公式如下：

其中，k（z）表示节点i和j的公共邻居z的度，？祝（i）表示节点i的所以邻居节点的集合。

然而，这种仅仅需要考虑网络进行局部信息来度量贴近度的指标会导致网络的过于局部最优，忽略了网络的整体构架，从而导致与实际研究结果有很大的偏差。基于此，甘立强[11]提出将两个节点间公共邻居的网络局部信息和两个节点间最短路径的网络全局信息进行整合，并定义了节点贴近度Sim（i，j）：

其中d（i，j）表示节点i和节点j之间最短路径的长度，n表示网络的节点总数。节点i，j可达是指节点i，j之间有边直接相连。当d（i，j）越大时，则贴近度矩阵Sim（i，j）中元素值就越小，也就意味着两个节点越不贴近。同时，两个节点之间如果没有直接联系，则意味着两个节点之间的信息交换主要依赖于相邻节点，因此忽略它，将贴近度设置为0。同时，乘以节点总数n从而可以适当进行放大结果，避免结果过小，超出计算机的计算能力范围。

然而，该算法忽略了节点可达但没有公共邻居的情况，这也可能造成与实际网络的较大偏差。该算法定义，如果两个节点之间有边，但没有公共邻居，则两个节点之间的贴近性为零。事实上，如果两个重要节点之间有一条边，但是由于没有一个共同的邻居，那么两个不同节点的度越大，它们发展之间的贴近度就越小，成反比关系，但并不意味着它们之间的贴近度就可以忽略不计。基于共同邻居的局部信息和节点间最短路径的全局信息，重新定义了节点贴近度，Sim（i，j）公式如下：

其中，i～j表示节点i和j互相连通。

2 基于节点贴近度的社区划分算法

2.1 衡量网络划分质量的指标

标准化互信息（NMI），为了量化被检测群落与被分割群落之间的贴近性，可以利用標准化交互信息（NMI）来评价群落划分的质量，NMI值的范围在[0，1]之间，越接近1，算法的效果越好，可以挖掘出更多的真实群落结构[12]。计算NMI值公式如下：

其中，N是节点数，A和B代表真实的社区，以及由算法划分的社区的结果。C表示模糊矩阵，矩阵中元素Cij表示属于A划分中的社区i的节点也属于B划分中的社区j的节点。

衡量簇结果性能另外一个最普遍的标准是模块度（Modularity），这是由Mark Newman等人[3]提出，最常用的衡量网络中社区分割质量标准的基本思想是将划分为社区的网络与相应的零模型进行比较，以衡量网络中社区的结构强度。一般模块度定义如下：

其中，ki是点i的度，函数？啄（ci，cj）的取值定义为：如果点i和j在一个社区，即ci=cj，则函数？啄（ci，cj）值为1，否则为0。m为网络中边的总数。Aij为网络的邻接矩阵的一个元素。

2.2 理论模型

每个节点在初始时刻都可以被视为一个社区，并且算法选择任意节点作为初始节点，所以本文算法不需要知道网络的先验信息，另外由于孤立节点在划分社区过程中意义不大，所以假设网络中没有孤立的节点。社区划分的目的是将具有贴近属性的节点划分到同一个社区中，因此本文先采用式（3）来计算节点之间的贴近度，构建一个贴近度矩阵MSN={Sij}，其中Sij表示节点i和j的贴近性程度。然后，再进行后续操作：将包含该节点的社区与包含与该节点最贴近的节点的社区合并，生成一个新的社区。确定下一个待处理节点。选择与当前节点最贴近的节点作为下一个节点。如果此新节点未包含在当前社区中，请转到前一步执行进一步合并。否则，将随机选择一个新的未访问节点作为初始节点，并在第一步执行一个新的社区合并。重复合并，直到网络中的所有节点都被访问，形成小的社区。

初步合并完节点之后，再进行小簇合并，所遵循的原则是如果簇之间合并完成后能提高所计算的NMI值，则进行合并，反之则不进行合并。重复此步骤，直到NMI最大时，结束过程。

根据节点贴近性度量的簇分割方法具体操作步骤总结如下：

（1）每个节点在初始时刻被视为一个社区，任何一个节点都被随机选为初始节点。

（2）然后计算节点贴近度矩阵S={Sij}，其中i=1，2，…，n，j=1，2，3…，n，从剩余的节点中选择最贴近的节点，并将它们合并成一个新的社区。

（3）最后，以新节点作为初始节点，寻找最贴近度的节点。如果发现的节点不在当前进行合并的社区中，则将该节点合并到该社区中，如果是，则随机进行选择其余未处理的节点中的一个可以作为研究初始节点返回（2）。

（4）重复迭代步骤（3），直至簇交互化信息NMI达到最大值，算法结束。最后计算了群落划分的结果以及对应的交互化信息NMI值和模块化Q值。

3 实验结果和分析

本文通过将其应用于划分四个真实网络和计算机生成的基准网络的社区结构，来评估所提出的贴近性度量的性能。四个实际网络的方法的实验数据，如表1所示。

3.1 Zachary空手道俱乐部网络

这个网络是一个经典的耗时两年收集整理的网络数据集，20世纪70年代的社会学家扎卡里观察了美国一所大学空手道俱乐部的34名成员的社会关系，基于这些成员在俱乐部内外的互动，一个社会网络被构建，由三十多个节点和七十多条边组成，两个节点之间的边表示相应的两个节点是亲密的朋友。在图1中，通过我们算法划分的两个簇用不同的数字表示，而该网络的真实组则用不同的颜色标记。如图1所示，本文算法MSN能够准确划分簇，NMI=1，没有节点被错误分类，因此，本文提出的贴近度量矩阵划分方法适用于空手道俱乐部网络划分。

3.2 海豚网络

该网络数据集是一个海豚社会关系网络，来自新西兰海峡六十二只海豚种群的交流。网络中含有62个节点以及159条边。节点代表单独的海豚，每条边代表两只海豚之间的频繁接触。

如图2所示，划分成两个簇，NMI=1，没有节点被错误分类，所以说本文算法MSN能够划分簇且效果非常好。

3.3 美国足球队网络

这个网络代表了115支大学橄榄球队，一个赛季的一百多个节点和六百多条边的时间表。网络中的每个节点代表某国橄榄球赛季的大学代表队，两个节点之间的边表明各自的球队之间至少进行了一场比赛。根据本文算法，该网络分为十二个簇。用代码将这些算法划分得到的社区用不同的数字表示，而该网络的真实组则以不同的颜色标记。如图3所示，有九个节点被错误分类，但NMI=0.9252274，NMI值接近1，整体划分较为明显。

此外，如表2所示，该算法计算的模块度高于其他三种算法，说明该算法的质量优于其他三种算法。

3.4 美国政治书籍网络

该网络是通过研究2004年总统竞选期间购买的一些美国政治书籍而建立起来的，其中有一百多个节点和四百多条边。节点代表美国在线书店出售的与美国政治教育相关的书籍，而边则代表一定数量且同时购买这两本书的读者，也就是说这两本书是同一个目标客户经常购买的。这些网络中的政治书籍主要分为三类：自由派、中间派和保守派。这些类别是由Newman根据书中观点进行人工分析综合销售平台上的评价而划分的。

根据本文算法，该网络分为三个簇。同样，我们用代码将这些算法划分得到的社区用不同的数字表示，而该网络的真实组则以不同的颜色标记。如图4所示，有十一个节点被错误分类，但错误率在合理范围内，NMI值较高，相比较而言，整体划分较为正确。

3.5 计算机生成网络

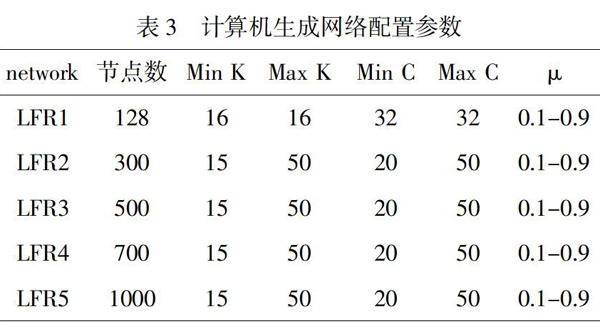
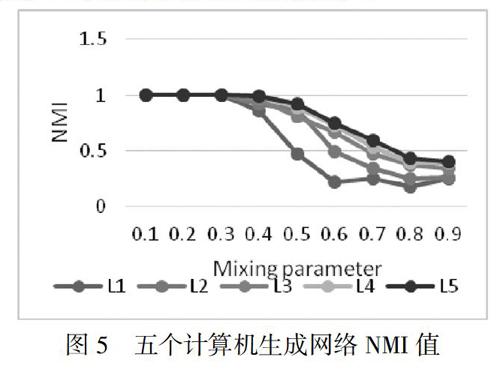
除了实际网络，还将此算法应用到著名的人工合成LFR（Lancichinetti-Fortunato-Radicchi）基准网络[15]中。在这个网络中，用一个混合因子？滋∈[0，1]测量群落结构的模糊化程度，值越低，表明群落结构的模糊化程度越低，清晰度越低，即簇組织结构越清楚[16]。基于不同大小的人工数据集计算NMI值。在实验过程中，创建了五个不同节点数的计算机生成网络，具体参数设定如表3所示，？滋值从0.1到0.9不等，NMI值结果如图5所示。

从图5中可以看出，当0.1≤？滋≤0.3时，所有网络都有较高NMI值，且NMI值都基本相等，说明此时划分算法在人工数据集上能够较为清晰地划分簇结构，而当？滋≥0.3时，这五个网络开始呈现差异，节点数越多的网络NMI值越高，随着混合参数值的增大，NMI值呈下降趋势，其中在0.4≤？滋≤0.8时，基本所有网络NMI值下降较为迅速。在图5中，网络的节点总数为1000，节点的平均度k=15，节点的最大度Max K=50，节点的最小度Min K=15，簇的最小尺寸Min C=20，簇的最大尺寸Max C=50，度指标td=2，簇指数tc=1。与文献中的标记传播算法相比，该算法具有更高的归一化互信息值，即其社区h的分割结果更加精确[4]。

4 结论

本文提出了作为一种可以基于节点贴近性的社区检测技术方法。首先定义节点间的贴近度，对小社区中最贴近的节点进行聚类。然后将这些社区合并，以找到一个稳定的社区结构。通过测试和与以前的社区检测方法的比较来验证。基于节点贴近性，提出了一种快速高效的检测网络中社区结构的算法，保证了一对贴近度较高的节点更有可能被分组为一个社区。它不需要事先知道整个网络的结构，并且比其他方法具有更低的计算复杂度。该算法已应用于各种信息网络，包括实际收集的网络和计算机生成网络，表明发现复杂网络的社区结构是相当有效地在实际和计算机生成的网络上取得的实验结果表明，本文的方法在发现通过网络中的社区组织结构设计方面具有非常有效。该方法是在无向无权网络的基础上发展起来的，可以推广到有向网络和加权网络，并包含某些参数，如权重、计算模块化的方向等。

参考文献：

〔1〕GIRVANM， NEWMANMEJ.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences，2002，99（12）：7821-7826.

〔2〕F.Chung， Spectra Graph Theory. American Mathematical Society， Providence， 1997.

〔3〕Clauset Aaron， Newman M E J， Moore Cristopher. Finding community structure in very large networks.. 2004， 70（6 Pt 2）：066111.

〔4〕Asgarali Bouyer，Hamid Roghani. LSMD：A fast and robust local community detection starting from low degree nodes in social networks[J]. Future Generation Computer Systems，2020，113.

〔5〕W. Li， C. Huang， M. Wang， X. Chen， Stepping community detection algorithm based on label propagation and similarity， Physica A： Statistical 365 Mechanics and its Applications 2017，472 ：145–155.

〔6〕Zheng-Hong Deng，Hong-Hai Qiao，Ming-Yu Gao，Qun Song，Li Gao. Complex network community detection method by improved density peaks model[J]. Physica A： Statistical Mechanics and its Applications，2019，526.

〔7〕孫宇.一种基于Jaccard贴近度的簇发现方法[J].电子技术与软件工程，2016（03）：20.

〔8〕Farshad Aghabozorgi， Mohammad Reza Khayyambashi. A new similarity measure for link prediction based on local structures in social networks. 2018， 501：12-23.

〔9〕T. Zhou， L. L， Y.C. Zhang， Predicting missing links via local information， Eur. Phys. J. B， 2009，71（04）：623–630.

〔10〕Peng Zhang， Dan Qiu， An Zeng， et al. A comprehensive comparison of network similarities for link prediction and spurious link elimination. 2018， 500：97-105.

〔11〕Ajay Kumar，Shashank Sheshar Singh，Kuldeep Singh，Bhaskar Biswas. Link prediction techniques， applications， and performance： A survey[J]. Physica A： Statistical Mechanics and its Applications， 2020：553.

〔12〕甘立强，王旭阳，燕楠，等.基于节点贴近度的簇划分方法研究[J].计算机与数字工程，2018，46（02）：213-217+240.

〔13〕NEWMAN M E J.Modularity and community structure in networks[J]. Proceedings of the National Academy of Sciences， 2006，103（23）： 8577 - 8582.

〔14〕梁宗文，杨帆，李建平.基于节点贴近性度量的簇结构划分方法[J].计算机应用，2015，35（05）：1213-1217+1223.

〔15〕LANCICHINETTI A，FORTUNATO S，RADICCHI F. Benchmark graphs for testing community detection algorithms[J]. Physical Review E，2008，78（04）：046110.

〔16〕DANON L， DIAZ-GUILERA A， DUCH J，et al. Comparing community structure identification[J]. Journal of Statistical Mechanics： Theory and Experiment， 2005（09）： P09008.