立足数学本质凸显数学价值

2021-08-12李静

教育实践与研究·小学课程版 2021年6期

李静

摘要：坐标系的建立在数学发展史上有着开创性意义，用代数方式研究图形的运动和变化，将数与形完美地结合在一起。小学数学“位置”教学是平面直角、极坐标系内容的初步渗透，这部分内容是培养学生数学抽象、直观想象、模型思想等数学素养的很好素材。教师应立足数学本质，设计数学活动，引导学生经历坐标系模型的抽象过程，感受其价值，进而发展学生数学素养。

关键词：小学数学;坐标系;数学抽象;直观想象;模型思想

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2021）16-0056-05

平面直角（极）坐标系的初步认识是21世纪小学数学课程改革的新增内容，是“图形与位置”课程内容的组成部分。各版本小学数学教材这部分内容的编排都创设了诸如教室座位、海上船只的位置等现实情境。教学时，教师们也多基于各种生活情境，引导学生建立规则（参照系）后，用数表示位置。在生活化的情境中进行学习虽然贴近学生的认知，但是如果囿于现实情境，就“位置”讲“位置”也会淡化坐标系的“数学味”。那么，如何立足坐标系的本质，感悟“位置”教学内容的数学价值，引发学生的数学思考呢？下面就从数学史的发展，课程内的安排和教学实施几个方面进行剖析。

一、图形的量化研究——从数学发展史看坐标系产生的意义

在相当长的数学发展史中，算数一直是几何的附庸。开创图形代数研究历史的是十七世纪法国数学家笛卡尔和费马，他们提出的坐标系模型将数与图形完美的结合在一起，开启了解析几何的现代数学研究。笛卡尔更多的精力放在了哲学方面，他在《方法论》中阐述了这样的观点：至于古代人的几何和近代人的代数，都是只研究非常抽象、看起来毫无用处的题材，前者始终局限于考察图形，直到把想象力累得疲惫不堪后才运用理解力;后者则一味地用规则和数字来约束，使人感觉晦涩枯燥、头昏脑胀，却得不到心灵的学问。正因为如此，我们才要寻找另一种方法，包含这些学问的长处，而没有他们的短处。

笛卡尔在《方法论》的附录《几何学》中实践的想法就是解析几何的方法。解析几何的基本方法是引进“坐标”，即对一个几何对象附上或标上数，从而完全刻画了这个对象。我们知道，研究物体的运动是需要参照系的，从这个意义上说，刻画图形的运动轨迹也必须借助参照系。解析几何的核心思想是建立一个参照系，借助参照系通过数量分析的方法研究几何图形及其运动变化。平面直角坐标刻画平面上任意一点的方法：在平面上做一对互相垂直的线，作为每一个点所参照的x轴和y轴，把这两条直线看成是有方向的数轴并且用同样的单位来度量;另外，用一条射线和一个角度也可以作为参照系，这就是极坐标系，牛顿和伯努利最早使用了极坐标系。同样是描述平面上点的位置，直角坐标系建立的是横纵坐标的方形网格，极坐标系建立的是旋转角的边与距离为半径的同心圆的网格。平面坐标系包括;平面直角坐标系、平面斜角坐标系、仿射坐标系、极坐标系等。利用坐标系不仅能推导出几何图形的代数表达式，还能够帮助我们利用几何直观来研究代数问题。

二、感悟坐标系思想——小学数学“位置”课程内容安排

小学数学课程分两部分来教学坐标系的初步认识，分别是平面直角坐标系和极坐标系的初步认识。基于小学生的年龄特点和认识水平，两部分内容在各版本教材中均创设了学生熟悉的生活情境。平面直角坐标系的初步认识一般都基于教室的座位、操场上的队列或电影院的座位等场景，在统一的规则下，用横、纵两个坐标参数，确定人（或物）的位置。极坐标系在生活中一般应用于导航，各版本教材也多采用公园场馆位置或海上船只位置等情境，用相对于参照点的距离（极径）和相对于某方向的旋转角度（极角）来确定位置。

虽然在现实情境中教学坐标系的内容，但是教学“确定位置”的目标并不止于会用数对等表示某个具体位置，更重要的是让学生体会这种“表示”的价值。《义务教育数学课程标准（2011版）》（以下简称《课标》）中给出了数对确定位置的实施建议：小青坐在教室的第3行第4列，请用数对表示，并在方格纸上描出来。在同样的规则下，小明坐在教室的第1行第3列应当怎样表示？需要先在方格纸上标明正整数刻度，希望学生能够把握数对与方格纸上点的对应关系，并且知道不同数对之间可以进行比较。这个过程有利于学生将来直观理解直角坐标系。教学用数对在方格纸上表示点的位置要引导学生经历空间结构化、抽象化的过程，有效地沟通初中阶段的直角坐标系内容，感知坐标系的表示方法及思想。那么，在教学中如何就这些内容更好的体现“坐标系”蕴含的数学本质和价值，发展学生的数学素养呢？下面结合“用数对确定位置”一课的教学实践谈一谈。

三、凸显数学本质——小学數学“用数对确定位置”教学实践

（一）摆脱生活情境的干扰，感悟数学规定的“合理性”

在生活中，人们用行列描述位置时并没有统一规律，往往因为现实情境不同而呈现多种结果。笔者曾多次在不同场合执教“用数对确定位置”一课。在情境引入环节笔者让学生描述自己在教室的位置。多数情况学生都会用“第几列，第几位”等语言描述，也就是先确定纵列，再确定横行来描述位置。但是有一次，几个学生无一例外的都表述为“第几排（或行），第几个”，也就是先确定在第几横行再确定在第几纵列。同样是描述位置，这个班的同学为什么会与其他班级情况不同？上完课笔者静下心来观察教室座位摆放才恍然大悟：这节课是在一个会议室上的，座位摆放类似于电影院的座椅排列方式，学生在确定位置时先找到在第几排（行），再确定在第几个（列）。而学生平时上课的教室桌椅都是按列摆放的。

在方格纸上用数对确定位置时，学生常出现的问题是习惯于先确定行再确定列（先确定纵坐标，再确定横坐标），这是学生阅读习惯“干扰”数学学习的结果。其实，我们并不用过分纠结数对的顺序在生活中的合理性，数对表示位置应关注的本质不在两个数谁先谁后的问题，而是一定要用两个数的信息，才能确定一个人的位置，即二维平面上点的位置要用两个参数来唯一的确定。因此在教学时笔者引导学生思考（图1）：

同学们对自己在教室的位置的描述有什么共同点？

曹培英老师说“当我们觉得数学的规定与学生的认知有冲突时，十有八九是我们没有真正理解数学。”数对表示的顺序有其数学的结构性和发展性。利用数轴（数轴是一维空间的参照系）可以确定一维空间中一个点的位置，在二维空间中需要再取一个维度的参数才能确定点的位置。故而，由数轴发展为平面直角坐标系，便有了先确定横坐标（列），再确定纵坐标（行）的规定。教学时教师可以设置这样的教学环节，引导学生感悟这种数学规定的“合理性”：

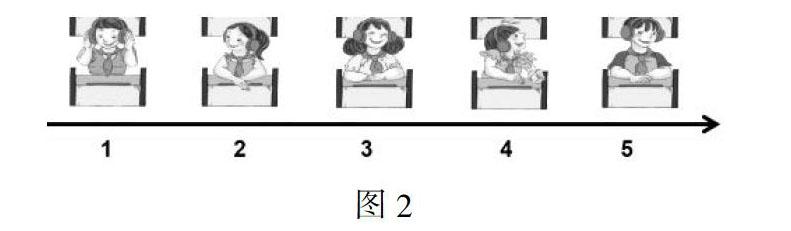
师：一年级的时候我们就曾经学习过用数表示位置。当同学排成一行时，我们可以用1，2，3，4……这样的一个数表示一个同学的位置（图2）。

师：当同学们排成几行时，我们就不能用一个数确定一个人的位置了，因为一个数对应了这样的一列同学。这时，我们要用同学所在列的信息，和行的信息共同确定一个人的位置（图3）。

在此基础上，三维空间需要再增加z轴上的坐标才能确定点的位置。教师可以引导学生观察生活进行思考：“同学们，你们去过菜鸟驿站取快件吗？你有没有注意过，我们的取件码是三个数。为什么菜鸟驿站的取件码需要三个数呢？”

（二）经历描述位置不确定的过程，体会参照系的价值

生活中位置的描述因观察视角的不同而具有相对性，因而要实现位置表示的唯一确定，一定要建立确定的参照系。用数对表示位置即建立数对与点之间一一对应的关系，前提也是建立唯一确定的参照系。教学中，教师要引导学生经历由在不同参照系描述位置到确定的参照系描述位置的过程，感受参照系的价值，掌握参照系的规则。

师：刚刚我们对自己在教室中位置的描述都用到了两个数，在数学上我们能不能用这样的两个数来表示位置呢？为了研究的方便我们请来了明明和他的同学。（图4）明明在这个班的位置可以用这样的一对数表示（4，2）。猜一猜哪个是明明？

学生在白板上勾画出明明的位置，并说明自己是怎样判断的（可以画出4个）。

师：这个班有4个明明！（生笑）你们找错了吧。是你们找错了还是我没说清楚啊？

师：我要说清楚什么条件你们就能准确的找到明明？（哪个数表示行，哪个数表示列，行和列按怎样的方向数）

以上的教学活动让学生经历了从不同的规则下描述位置不确定的“尴尬”，进而体会到要描述大家可交流的位置信息，就要建立唯一确定的坐标系。即确定原点和正方向及单位长度（由于小学阶段只涉及正整数，所以坐标系只限于第一象限，并且也不用考虑单位）。笔者在教学时设计了一个数学活动，让学生通过推理掌握规则，发展推理能力。

师：这个同学的位置可以用数对（2，2）表示（图5），通过这个数对你能找到明明（4，2）的位置并说出写数对的规则吗？

（三）经历由座位图到坐标系的抽象过程，体会模型思想

数学是对客观现象抽象概括后形成的科学语言和工具，因此数学教学不能只停留在生活场景中，而是要将这些生活现象进一步抽象概括生成数学结构，并解释生活。教学中，在用数对描述教室中的位置后，教师还要借助信息技术手段，引导学生经历坐标系抽象、建构的过程：将列和行对应横纵坐标，将学生座位抽象成点。形成坐标系模型后，再引导学生继续思考，还有哪些生活场景可以用此模型解释。

师：如果把图3中的同学变成一个个的点，你还能用数对表示这些点的位置吗（图6）？用数对表示点A、B、C的位置，D点和A、B、C组成一个长方形，D点的位置用哪个数对表示？

师：这一个个点可能是坐在教室的同学，还可能是中药铺中的一个个药箱（图7），还可能是公园中一个个的场馆（图8），还可能是几何图形中的点（图9）。你想想，这一个个点还可能是什么……

建立模型思想是学生体会和理解数学与外部世界的联系，而且也是实现上述目的的基本途径。教师要设计数学活动，引导学生经历“问题情境——建立模型——求解驗证”的建构数学模型的过程。

（四）用数对描述图形的运动变化，体会数形结合的思想

坐标系不仅限于表示点的位置，更本质的在于描述几何对象的性质和运动，尤其是描述函数图像。囿于小学生的知识储备和思维水平，教学中不宜过多渗透函数知识。但是，就位置讲位置未免又将富含“数学味”的内容教成了“白开水”，错失了感受解析几何数形结合思想精髓的良机。因此，教师可以设计一些适于学生年龄特点的有趣的数学活动，引导学生感悟坐标系在表示图形运动和性质上的优势和特点，感悟解析几何数与形完美结合的妙处。

师：请位置为（3，1）（3，2）……（3，6）的同学站起来。我叫起的同学组成了什么图形？

师：谁能像我这样用数对叫起几个同学组成一个几何图形？

在此基础上，教师还可以引入含有字母的数对，让学生想象图形。如：想象（3，x）（x，x）等组成的图形。还可以在抽象的坐标系设计一些几何图形的位置及变化的练习题目。

如图（图10），三角形ABC为直角三角形，则C点的位置用数对表示为（）。

以上数学活动可以让固定的点的位置“动起来”，学生在头脑中将图形与数之间进行互相转换，发展直观想象能力，感悟解析几何的本质。

总之，教师要深入挖掘蕴含于“坐标系”内容的数学本质，并基于学生的认知水平进行教学，引导学生在数学活动过程中发展数学素养，体会数学学习的价值。

参考文献：

[1]笛卡尔.方法论[M].王太庆，译.北京：商务印书馆，2000：第二部分.

[2]R·柯朗.什么是数学——对思想方法的基本研究[M].左平，译.上海：复旦大学出版社，2018.

[3]史宁中.数学思想概论[M].长春：东北师范大学出版社，2015：第2辑.

[4]刘加霞.数与点之间的一一对应是数对确定位置的根本[J].小学教学，2014，（04）.

[5]教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.