基于改进MOEA/D的多目标置换流水车间调度问题
2021-08-12李林林刘东梅王显鹏
李林林,刘东梅,王显鹏,3+
(1.东北大学 智能工业数据解析与优化教育部重点实验室,辽宁 沈阳 110819;2.沈阳中医药学校 计算机系,辽宁 沈阳 110300;3.东北大学 辽宁省智能工业数据解析与优化工程实验室,辽宁 沈阳 110819)
0 引言
流水车间调度问题(Flowshop Scheduling Problem, FSP)是一类经典的调度问题,被广泛应用于自动化、工业生产等领域。近年来由于多目标生产调度问题的广泛应用,多目标流水车间调度问题的研究受到了越来越多学者的关注。
学者们对多目标流水车间调度问题的优化求解研究很多,YENISEEY等[1]对多目标的流水车间调度问题进行了系统性的综述,指出基于群体的演化算法是求解中大规模的多目标流水车间调度问题的有效方法。基于群体的演化算法具有较好的并行性、全局性和扩展性,成为越来越多学者求解多目标问题的研究热点。吴秀丽等[2]研究了一种考虑可再生能源的多目标柔性流水车间调度问题,提出了集成低碳调度策略的快速非支配排序遗传算法对问题进行高效求解;LI等[3]提出了基于分解的多目标离散人工蚁群算法对考虑工序启动时间的置换流水车间调度问题进行求解,算法使用扰动算子对种群进行进化,并设计了局部搜索方法改进解集的质量;LU等[4]提出一种混合多目标回溯搜索算法求解考虑完成时间和能效的多目标置换流水车间调度问题;WANG等[5]设计了一种用于多模式优化问题的物种机制,提出了基于物种的具有多种群策略的多目标进化算法,对流水车间调度问题进行求解;TIWARI等[6]提出一种基于Pareto组块的分布估计算法求解多目标置换流水车间调度问题,算法采用二元概率模型生成组块,改进非支配解集的多样性;付亚平等[7]提出一种基于分解的多种群遗传算法,根据种群分布为当前子问题构造多个子种群,实现多目标置换流水车间调度问题的求解。
基于分解的多目标进化算法(Multi-objective Evolutionary Algorithm based on Decomposition, MOEA/D)可以将多目标问题分解为多个子问题进行求解,具有较强的搜索能力、高效的适应度评价和良好的收敛速度,近年来成为多目标进化算法研究中的热点。JIANG等[8]提出一种基于分解的多目标遗传算法,对以工期和能源消耗最小化为目标的考虑工序启动时间的置换流水车间调度问题进行了求解,算法提出一种动态策略对个体进行交配,并使用局部强化策略来提高算法的局部开采能力;ZANGARI等[9]提出一种基于分解的MEDA/D-MK算法对多目标置换流水车间调度问题进行求解,对每个子问题建立马洛尔核模型,并利用扰动操作保证非支配解集具有更好的分布性;CHANG等[10]基于MOEA/D算法框架研究了不同种群替换策略的作用,并结合邻域搜索对以工期和总加工时间为目标的流水车间调度问题进行求解;ALHINDI等[11]将MOEA/D算法与禁忌搜索算法相结合对置换流水车间调度问题进行了求解。
以改进非支配解集的分布性和收敛性为目的对经典算法进行改进,成为多目标进化算法研究的重要分支之一。局部搜索方法能够加强对解空间的集中开采,提高解的质量,将局部搜索策略应用于进化算法能够很好地改进算法的收敛性;LI等[12]提出一种基于分解的局部搜索算法求解多目标置换流水车间调度问题,使用基于插入的邻域搜索、多邻域搜索策略和双扰动机制对解进行邻域开采;XU等[13]提出迭代邻域搜索方法求解考虑工序启动时间的置换流水车间调度问题,算法利用外部存档中的非支配解作为局部搜索的开始点,利用基于Pareto的可变深度搜索策略平衡算法的全局探索能力和局部开采能力;模因算法[14-15]直接将局部搜索策略作为算法的标准组件,提高算法的性能。将局部搜索方法引入多目标进化算法,提高非支配解集的收敛性和分布均匀性是多目标进化算法改进研究的研究方向之一。但是由于局部搜索策略需要较多的计算时间,提高邻域搜索的效率也是非常重要的。基于邻域的局部搜索策略对改进算法求解流水车间调度问题解的质量起到了关键性作用,一些研究虽然通过邻域搜索策略提高了解的质量,但是却需要花费较高的计算时间进行大量的甚至盲目的邻域开采。尤其是将算法推广到实际生产调度问题时,因为需要加入其他实际要求和特征,将使问题的求解更加复杂进而影响算法应用效果,所以研究高效的邻域搜索策略对研究多目标流水车间调度问题的求解和应用非常重要。
外部存档[2,8-10,13-15]通常用于保存搜索过程中生成的非支配解,一方面作为输出结果集,另一方面可以为种群进化提供丰富的过程信息。对外部存档设计优良的局部搜索策略,能够有针对性地改进非支配解集的收敛性和分布均匀性。受该思想的启发,为高效求解多目标置换流水车间调度问题,本文提出一种改进的MOEA/D算法,即在MOEA/D算法框架中嵌入基于分组和统计学习机制的两阶段邻域搜索策略改进外部存档的质量。算法一方面利用外部存档为种群进化提供全局信息,提高算法的全局能力;另一方面,利用两阶段的邻域搜索策略改进外部存档,提高非支配解集的收敛性和分布的均匀性。
本文的主要工作包括:
(1)利用外部存档为种群进化提供父代个体,提高算法全局探索能力。
(2)基于分组和统计学习机制提出两阶段邻域搜索策略改进外部存档:利用分组机制对目标空间进行划分选择代表个体,提高多目标搜索的效率,改进非支配解集的均匀性;利用统计学习策略获取邻域搜索的位置信息,改进非支配解集的逼近性,提高邻域搜索的效率。
(3)利用基于距离的替换策略更新种群,保证子问题与权重向量分布趋于一致,提高种群的多样性,同时保证分组机制的有效性。
(4)将所提算法与MOEA/D[16]、NSGA-Ⅱ(fast elitist non-dominated sorting genetic algorithm)[17]和MEDA/D-MK(multi-objective decomposition-based mallows models estimation of distribution algorithm)[9]进行对比分析,证明所提算法的优越性。
1 多目标置换流水车间调度问题
流水车间调度问题是许多实际流水线生产调度问题的简化模型,是典型的NP-hard问题。流水车间调度问题可以描述为n个工件在m台机器上加工,每个工件加工任务由m道工序完成,每道工序由不同的机器负责。假定所有工件具有相同的工艺线路,确定每台机器上工件的加工顺序,使工期、总加工时间等目标最小化。置换流水车间调度问题(Permutation Flow shop Scheduling Problem, PFSP)是对流水车间调度问题的进一步约束,约定所有机器上所有工件的加工顺序均相同。
置换流水车间调度问题可以使用π={π1,π2,…,πn}表示n个工件的调度顺序,Π表示所有可能调度的集合,π∈Π。πi表示第i个被调度的工件(i=1,…,n),j表示第j个用于加工的机器(j=1,…,m),Tπi,j表示工件πi在机器j上的加工时间,C(πi,j)表示工件πi在机器j上的加工完成时间,Cmax(π)表示按π顺序加工所有工件的完工时间,即工期;TFT表示所有工件的总加工完成时间。本文研究工期和总加工完成时间两目标最小化的PFSP问题,问题模型可以描述为式(1)~式(7)。
f1(π)=Cmax(π)=argminC(πn,m);
(1)

(2)
F(π)={minf1(π),minf2(π)},π∈∏。
(3)
s.t.
C(π1,1)=Tπ1,1;
(4)
C(πi,1)=C(πi-1,1)+Tπi,1,i=2,…,n;
(5)
C(π1,j)=C(π1,j-1)+Tπ1,j,j=2,…,m;
(6)
C(πi,j)=max(C(πi-1,j),C(πi,j-1))+
Tπi,j,i=2,…,n,j=2,…,m。
(7)
其中约束(4)~(7)描述了各工件加工完成时间的计算过程。约束(4)描述了第一个工件π1在第一台机器上的加工完成时间为其加工时间Tπ1,1;约束(5)描述了工件πi(i=2,…,n)在第一台机器上的加工完成时间,为前一工件πi-1的加工完成时间与πi在机器在机器1上的加工时间之和;约束(6)表示工件π1在机器j上的加工完成时间,为其在前一台机器上的加工完成时间,加上其在机器j上的加工时间;约束(7)描述的是工件πi在机器j(j=2,…,m)上加工完成时间与前一工件πi-1、前一台机器j-1之间的关系,保证工件πi-1在机器j上已经完成加工,且πi在前一台机器上也已经完成加工。约束(5)和(7)保证同一时刻一台机器上只能加工一个工件,约束(6)和(7)保证在同一时刻每一工件只能由一台机器加工。
2 经典MOEA/D算法
MOEA/D是基于分解的多目标进化算法中的典型范例,其改进研究已成为近年来的研究热点[10-11,18]。MOEA/D将多目标优化问题利用权重向量转化为多个单目标子问题,权重向量负责对目标空间进行划分,种群的选择、进化和更新操作则在由多个权重向量构成的邻域中进行。
2.1 适应值评价
在MOEA/D框架中,通常使用切比雪夫聚合函数评价子问题,如式(8)所示:
(8)
式中:λ=(λ1,λ2,…,λk)为当前子问题的权重向量;k表示多目标优化问题目标的维数;z*=min{fi(x)|x∈X}为参考点。
2.2 权重向量
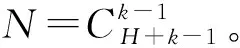
λ1+λ2+…+λk=1;
(9)
(10)
2.3 邻域
在MOEA/D算法中,邻域是种群选择、进化和更新操作的范围,邻域的初始化是根据各权重向量之间的欧式距离进行设定的。对权重向量λi确定其邻域的方法为:计算λi与各权重向量之间的欧氏距离,选择欧式距离最小的T个权重向量作为邻域;通过邻域内的子问题的相互协同和信息交换完成种群进化。
2.4 MOEA/D算法流程
步骤1初始化。
(1)初始化均匀权重向量λ=(λ1,λ2,…,λk)并划分邻域,即第i个权重向量的邻域B(i)={i1,i2,…,iT},i=1,2,…,N;
(2)初始化种群X=(x1,x2,…,xN),计算个体xi的函数值FVi=F(xi),i=1,…,N;

步骤2对种群中个体xi进行进化,i=1,2,…,N。
(1)从个体xi的邻域B(i)中选择两个随机个体,利用交叉、变异操作生成后代个体y;
(2)应用问题的修正或改进策略生成y′;
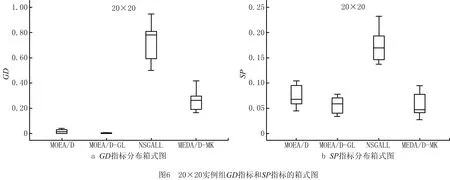
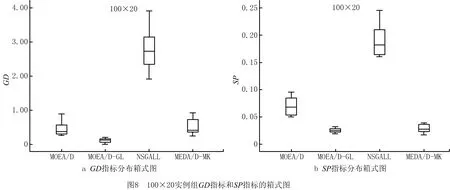
(3)如果fj(y′) (4)更新邻域解,即对t∈B(i),如果g(y′|λt,z)≤g(xt|λt,z),则xt=y′,FVt=F(y′)。 步骤3若满足终止条件,则算法停止并输出最优解;否则转步骤2继续执行。 为提高最优解集的收敛性和分布性改进算法的性能,本文在MOEA/D算法框架下提出一种基于分组和统计学习外部存档策略的改进MOEA/D算法(MOEA/D with a Grouping and statistical Learning mechanism, MOEA/D-GL),算法流程如图1所示。首先初始化参数和权重向量,根据权重向量之间的欧式距离确定邻域,并对权重向量进行分组;然后初始化种群(种群规模为NP),并计算切比雪夫聚合函数值,再利用非支配解初始化外部存档;在种群进化中,分别从邻域和外部存档中选择父代个体生成后代个体,利用基于垂直距离的替换策略更新种群,并更新外部存档;最后利用分组和统计学习的两阶段邻域搜索改进外部存档,当终止条件满足时,输出外部存档中的非支配解。 利用权重向量分组机制对外部存档中非支配解进行分组,可以从均匀划分的目标空间中选择代表个体,再对代表个体进行多目标邻域搜索。由于多目标邻域搜索需要消耗较多的计算时间,从不同的分组中选择代表个体对每个均匀划分的目标空间进行搜索,能够保证解集的分布性同时提高算法效率。为了描述外部存档中个体与权重向量之间的关系,在将个体加入外部存档时,保存对应子问题的编号。 本文以工件的加工顺序作为个体表达,即x={π1,π2,…,πn},其中πi为第i个调度的工件。例如对于有4个工件的问题,个体{4,2,1,3}表示工件4第1个在各台机器上加工,其次是工件2和工件1,工件3最后依次在各台机器进行加工。 (11) 3.5.1 选择操作 种群进化中父代个体的选择会直接影响后代个体的质量。在传统MOEA/D算法中,父代个体全部从当前子问题的邻域中选取,这种方式对邻域参数T非常敏感,T越大,算法的全局性越好,但是局部性变差;反之,T越小,算法的局部性越好,但是全局性越差。而外部存档能够提供进化过程的历史全局信息,以更好地平衡种群进化的全局能力和局部能力。本文从邻域中选择一个父代个体,另一个父代个体从外部存档中随机选择,从而更好地利用局部信息和全局信息,产生更有希望的后代个体。 3.5.2 交叉操作 交叉操作能够将父代个体中的基因信息传递给后代个体。使用邻域和外部存档中的随机个体作为父代个体,利用两点交叉(Two-Point Crossover, TPX)算子[21]进行交叉操作产生后代个体,交叉操作如图2所示,其中P1为邻域中随机选择的个体,P2为外部存档中的随机个体。通过TPX交叉操作得到个体y。 3.5.3 变异操作 变异操作可以提高种群的多样性,本文通过对生成的个体y随机交换两个位置上的工件实现变异操作,生成后代个体y′,变异操作如图3所示。 3.5.4 替换操作 进化生成的后代个体用于更新种群,MOEA/D算法的替换操作主要有局部替换策略[18]、全局替换策略[22]和基于距离的替换策略[23]等。文献[23]分析了子问题与权重向量之间的关系,指出仅依赖聚合函数更新种群容易导致个体的选择被误导。采用基于距离的替换策略更新种群能够同时考虑个体的质量和与权重向量之间的距离,使多样性和收敛性得到平衡。同时,基于距离的替换策略能迫使子问题与权重向量的分布趋于一致,同时保证基于权重向量分组后,可以从不同目标区域均匀的选择代表个体。 外部存档的作用是保存进化过程中的非支配解,利用Pareto关系更新外部存档能够保证解的最优性。当外部存档中非支配解总数超过容量限制时,则根据个体之间拥挤距离[17],依次删除拥挤距离最小的个体,直到外部存档中个体的数量满足最大容量,这种更新方式能够保证非支配解集分布的均匀性。 为了保证非支配解集逼近性和均匀性两方面的要求,本文提出一种基于分组和统计学习机制的两阶段邻域搜索策略改进外部存档质量。 3.7.1 外部存档分组机制 IREDI等[24]第一次提出了分组策略,分组能够体现一组个体之间的相似特征,利用3.2节中权重向量分组机制实现对外部存档中非支配解集的分组,进而实现不同目标空间的探索与开采。基于距离的替换策略能够更好地保证非支配解与权重向量分布趋于一致,从而保证了分组策略的有效性。 3.7.2 统计学习策略 3.7.3 两阶段邻域搜索策略 在分组和统计学习策略基础上,提出了两阶段邻域搜索策略改进外部存档质量,以提高非支配解集的收敛性和分布均匀性。在均匀性方面,利用分组机制从不同的目标区域选择代表个体进行多目标搜索,提高外部存档中非支配解的数量和均匀性;在收敛性方面,利用权重向量加权方法对个体进行单目标优化,改进非支配解的收敛性。 阶段Ⅰ基于分组和统计学习的多目标搜索策略。 基于分组机制从外部存档中选择代表个体,利用统计学习策略得到各位置的标准偏差信息,然后对代表个体xk(k=1,…,K)进行多目标贪婪搜索,dmax表示邻域搜索的最大长度。具体过程如下: 步骤2基于标准偏差信息利用轮盘赌方法确定搜索的开始位置p。 步骤3以代表个体xk从位置p开始的d个工件构成集合B=(b1,b2,…,bd),去掉集合B中工件后得到的部分解记作pk,设集合P0={pk}。 步骤4for(i=1;i≤d;i++) (1)将工件bi依次插入集合Pi-1中解的所有可能位置,得到集合Pi; (2)去掉集合Pi中被支配的解。 步骤5利用集合Pd更新外部存档。 步骤6对新加入外部存档中的解y,计算解y与所有权重向量之间的垂直距离,保存具有最小垂直距离的权重向量的编号。 对于非支配解数量为0的分组,则从种群中属于该分组的子问题中随机选择一个作为代表个体进行多目标搜索策略。由于多目标搜索策略需要大量进行非支配关系比较,利用分组策略可以从均匀划分的目标空间选择代表个体,能够高效地在不同目标空间区域进行开采,增加外部存档中非支配解的数量及提高均匀性。基于统计学习的方法能够更好地获取邻域搜索的位置信息,进一步提高搜索的效率。 阶段Ⅱ基于权重向量加权的单目标搜索策略。 在阶段Ⅰ之后,对外部存档中所有个体进行单目标邻域搜索,改进非支配解的收敛性。对非支配解xk(k=1,2..|EP|)进行单目标局部搜索过程如下: 步骤2基于标准偏差信息利用轮盘赌方法确定搜索的开始位置p。 步骤3对解xk中从位置p开始的d个工件构成集合B=(b1,b2,…,bd),去掉集合B中工件后得到的部分解记作pk,设集合P0={pk}。 步骤4for(i=1;i (1)将工件bi依次插入集合Pi-1中解的所有可能位置,得到集合Pi; (2)利用解xk的权重向量计算集合Pi中解的加权目标函数值,仅保留具有最小目标函数值的解。 步骤5将工件bd依次插入集合Pd-1的所有可能位置,得到集合Pd。 步骤6去掉集合Pd中被支配解。 步骤7利用集合Pd更新外部存档; 步骤8对新加入外部存档中的解y,计算解y与所有权重向量之间的垂直距离,保存具有最小垂直距离的权重向量的编号。 阶段Ⅱ的邻域搜索策略利用权重向量将两目标问题转换为单目标问题,利用单目标贪婪搜索改进非支配解集的收敛性。 本文采用TAILLARD[25]中的110个PFSP的标准测试算例进行测试。依据规模将110个测试实例分为11个分组,每个分组包括10个实例,本文利用n×m描述问题的规模。其中,工件数量n从{20,50,100}中选取时,机器数量m从{5,10,20}中选取。当工件数n=200时,机器数m从{10,20}中选取。 表1 ANOVA分析结果 为了验证所提算法的有效性,将MOEA/D-GL算法与MOEA/D、NSGA-Ⅱ、MEDA/D-MK算法进行比较。所有算法在同一台机器上进行测试,算法参数设置均与原始文献相同,停止准则为最大评价次数Tmax设置为60 000,每个实例单独运行10次得到平均GD指标和SP指标,并利用ANOVA方法进行方差分析,置信水平设置为95%。 如表2和表3所示为4个算法得到11个分组的GD指标和SP指标的均值。其中,最好的性能指标用斜体加粗表示,在MOEA/D、NSGA-Ⅱ、MEDA/D-MK列上,“+”表示MOEA/D-GL算法显著优于对应的MOEA/D、NSGA-Ⅱ、MEDA/D-MK算法;“-”表示MOEA/D-GL算法显著劣于对应的MOEA/D、NSGA-Ⅱ、MEDA/D-MK算法;“=”表示MOEA/D-GL算法与MOEA/D、NSGA-Ⅱ、MEDA/D-MK算法没有显著性差异。 由表2结果可知,MOEA/D-GL算法几乎得到了所有分组的最好平均GD指标。与MOEA/D算法相比,MOEA/D-GL算法得到GD指标有6组显著优5组没有显著性差异的结果;与NSGA-Ⅱ算法相比,MOEA/D-GL算法得到了全部11组的显著优的结果;相比于MEDA/D-MK,MOEA/D-GL算法得到了9组显著优2组没有显著性差异的结果。只有在200×10规模的实例分组中,MEDA/D-MK算法得到了更好的平均GD指标,但二者的GD指标没有显著性差异。这说明MOEA/D-GL算法在收敛性方面相较于其余3个算法有明显优势。MEDA/D-MK算法在求解大规模问题时,收敛性也很好,尤其是对于200×10规模分组得到最好的GD指标。在小规模和中等规模问题(20×20、50×5、50×10、50×20、100×5)求解时,MOEA/D算法得到的GD指标与MOEA/D-GL算法没有显著性差异,但是在对大规模问题求解方面,收敛性显著劣于MOEA/D-GL算法。而NSGA-Ⅱ算法相比于其他3个算法收敛性表现较差。MOEA/D-GL算法在收敛性方面表现优越的原因可能是由于: (1)算法利用外部存档为种群进化提供全局较好地父代个体,防止种群进化陷入局部最优,较好地平衡了全局探索能力和局部开采能力; (2)利用统计学习策略得到邻域搜索位置,利用权重向量对多目标问题进行单目标评价和单目标贪婪搜索提高了非支配解集与Pareto前沿的逼近性; (3)另外,利用分组机制和统计学习策略能够提高算法的效率,对提高解集的收敛性也具有积极的作用。 表2 各算法得到的平均GD指标 表3 各算法得到平均的SP指标 由表3结果可知,MOEA/D-GL算法在平均SP指标方面,在11种规模分组中得到了5组最好SP指标,MOEA/D算法得到1组最好的SP指标,MEDA/D-MK得到了5组最好的性能指标。从显著性上看,与MOEA/D相比,MOEA/D-GL算法得到7组显著优4组没有显著性差异的SP指标;与NSGA-Ⅱ相比,MOEA/D-GL算法得到了10组显著优,仅有一组的SP指标与NSGA-Ⅱ没有显著性差异;而MOEA/D-GL算法与MEDA/D-MK算法的SP指标没有显著性差异。说明所提算法在改进非支配解集的分散性方面是有竞争力的。分析MOEA/D-GL算法在分散性方面表现较好的原因可能是由于:①种群进化中使用了基于个体与权重向量垂直距离来更新种群,使种群具有更好的多样性;②利用分组机制从目标空间均匀地选择代表个体,并进行多目标邻域搜索,改进了非支配解集分布的均匀性。由于MEDA/D-MK算法利用强扰动操作改进非支配解集的多样性,分散性也很好。而MOEA/D算法和NSGA-Ⅱ算法缺少必要的策略对多样性进行管理,因此SP指标相对较差。 如图6~图9所示为20×20、50×20、100×20和200×20实例组GD指标和SP指标分布的箱式图,进一步说明了MOEA/D-GL算法在收敛性和分布均匀性方面是有竞争力的。如图10所示为4种算法得到的关于实例Ta030、Ta060和Ta090和Ta110的非支配前沿的分布图,用来描述小规模、中等规模、较大规模和大规模实例求解中非支配前沿的分布情况。对于小规模实例Ta030,MOEA/D-GL算法、MOEA/D算法得到解集的分散性和分布均匀性都较好,MEDA/D-MK算法非支配解集的均匀性和宽广性很好,收敛性相对欠佳,NSGA-Ⅱ算法收敛性和均匀性方面均表现较差;对于中等规模实例Ta060和较大规模实例Ta090的求解,MOEA/D-GL算法的收敛性较好,MEDA/D-MK的分散性和宽广性更好,但收敛性相对差,MOEA/D算法的收敛性较好,但是均匀性相对较差;对于大规模实例Ta110,MOEA/D-GL算法在收敛性方面优于其他算法,均匀性方面也是有竞争力的。因此,从得到非支配解集的收敛性和均匀性两方面综合评价,说明MOEA/D-GL算法性能是优越的。 基于MOEA/D框架,本文提出一种改进的分解多目标进化算法(MOEA/D-GL),对双目标的PFSP问题进行求解。算法利用外部存档为进化提供全局信息生成后代个体,防止进化陷入局部最优,平衡算法的全局探索和局部开采能力;利用基于距离的替换策略更新种群,提高了种群的多样性。为了从收敛性和分布均匀性两方面改进算法,提出了基于分组和统计学习机制的两阶段邻域搜索策略改进外部存档。通过对MOEA/D-GL算法与MOEA/D、NSGA-Ⅱ和MEDA/D-MK算法的显著性分析和比较实验,说明MOEA/D-GL算法在收敛性方面性能优越,分布均匀性方面也是有竞争力的。下一步,将对算法中的参数进行自适应控制研究,并将其应用于实际生产调度问题中。3 改进的MOEA/D算法
3.1 算法框架

3.2 基于权重向量的分组机制
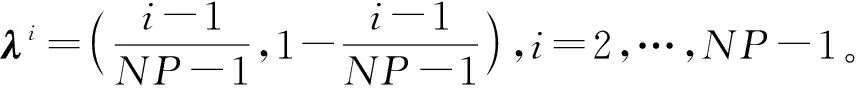
3.3 个体表达
3.4 种群初始化与评价

3.5 种群进化策略


3.6 外部存档更新机制
3.7 外部存档改进策略


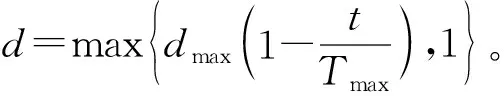
4 实验分析
4.1 测试问题
4.2 环境及参数设置
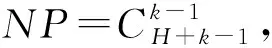
4.3 参数敏感性分析
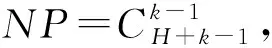

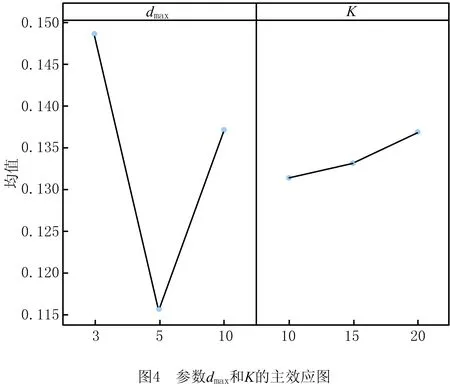

4.4 算法比较与分析





5 结束语
