等截面波纹腹板钢箱组合连续梁自振特性
2021-08-12张紫辰王根会金学军
张紫辰,王根会,樊 江,金学军
(1.兰州交通大学土木工程学院,甘肃兰州 730070;2.甘肃省交通规划勘察设计院股份有限公司,甘肃兰州 730070)
自1986年法国建成世界上第1座波纹钢腹板组合箱梁桥—Cognac 桥以来,波纹钢腹板组合梁桥在各国公路、铁路以及城市轨道交通建设领域得到了长足的发展[1-3],如日本黑部川铁路桥即为该类结构[4]。然而,传统波纹钢腹板组合箱梁在正弯矩作用下,易出现混凝土底板受拉开裂的病害。为此,国内学者提出了波纹腹板钢箱组合梁桥,这种新型组合结构采用平钢板取代了传统波纹钢腹板组合箱梁的混凝土底板,充分利用了混凝土顶板抗压、钢底板抗拉以及波纹钢腹板抗剪屈服强度高等优点,有效解决了温度应力和收缩、徐变等因素带来的结构病害,进一步减轻了结构自重,增大了桥梁的跨越能力[5]。由于我国地形复杂、幅员辽阔,因而该类桥型在我国公路和铁路建设中具有广阔的应用前景。但是由于受剪力滞后、剪切变形和褶皱效应的影响,波纹钢腹板组合桥梁的受力非常复杂。近年来,通过众多学者的不懈努力,传统波纹钢腹板组合桥梁静、动力学性能的研究日趋完善,许多成果已应用于该类桥梁的设计中[6-10]。但是针对这种新型的波纹腹板钢箱组合连续梁桥自振特性的研究还不多见[11-12],由于该类新型组合结构质量主要集中在箱梁的顶板,因而其中性轴上移,与传统波纹钢腹板组合箱梁相比,新型组合结构的自振特性与之存在较大差异[13],因此,波纹腹板钢箱组合连续梁桥自振特性的研究就显得更为重要。
本文基于能量变分原理,综合考虑剪力滞、褶皱效应、剪切变形和转动惯量的影响,推导波纹腹板钢箱组合连续梁桥的动力学弹性控制微分方程和自然边界条件,结合模型试验和有限元数值模拟对波纹腹板钢箱组合连续梁桥的自振特性进行分析。
1 振动方程的建立与求解
图1 为波纹钢腹板的波折形状图。其中:tw为波纹腹板厚度;hw为波纹腹板高度;L1为平板长度;L2为斜板长度;δ 为波折角。波形钢腹板有效剪切模量Gw计算式[14]为
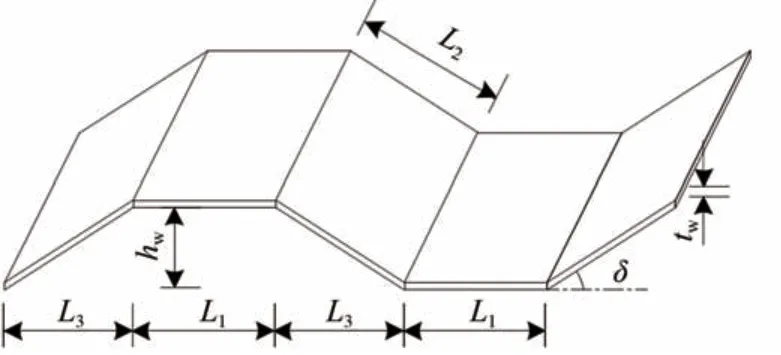
图1 波纹钢腹板形状示意图
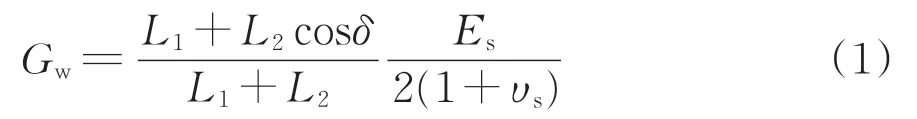
式中:Es为钢材弹性模量;υs钢材泊松比。
新型波纹腹板钢箱组合梁由混凝土顶板、钢底板以及波纹钢腹板组成,如图2 所示。图中:b2为悬臂板宽度;t1为上翼板混凝土厚度;2b1为混凝土顶板宽度;t2为钢底板厚度;h1和h2分别为顶板和底板的中心到形心轴的距离;z 轴为组合箱梁的高度方向;y轴为组合箱梁的宽度方向。
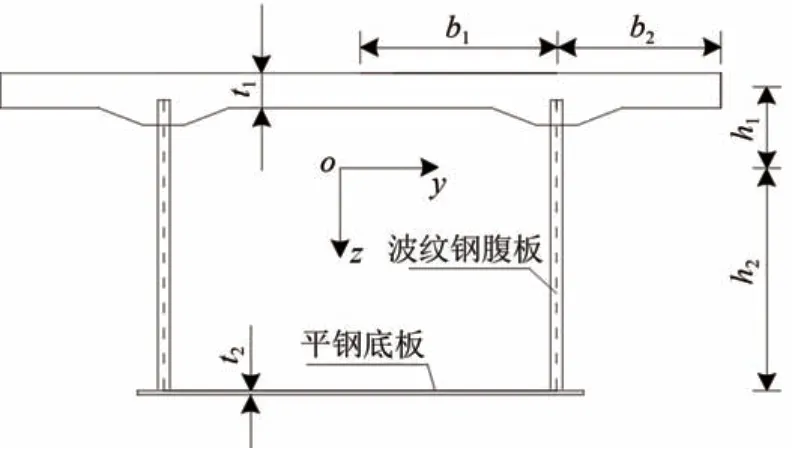
图2 波纹钢腹板组合箱梁
理论计算时,采用换算截面法将组合箱梁混凝土顶板换算为等效钢板,换算后的等效顶板厚度td和换算后等效顶板材料质量密度ρd分别为

式中:Ec为混凝土弹性模量;ρc为混凝土质量密度。
在对称弯曲状态下设结构的跨度为l,截面竖向动挠度为w(x,t),为准确描述其位移,引入截面轴向动位移函数Z(x,y,z,t);考虑剪切变形的影响,则箱梁顶板轴向位移Z1(x,y,z,t)、箱梁悬臂板轴向位移Z2(x,y,z,t) 和底板轴向位移Z3(x,y,z,t)可分别表示为
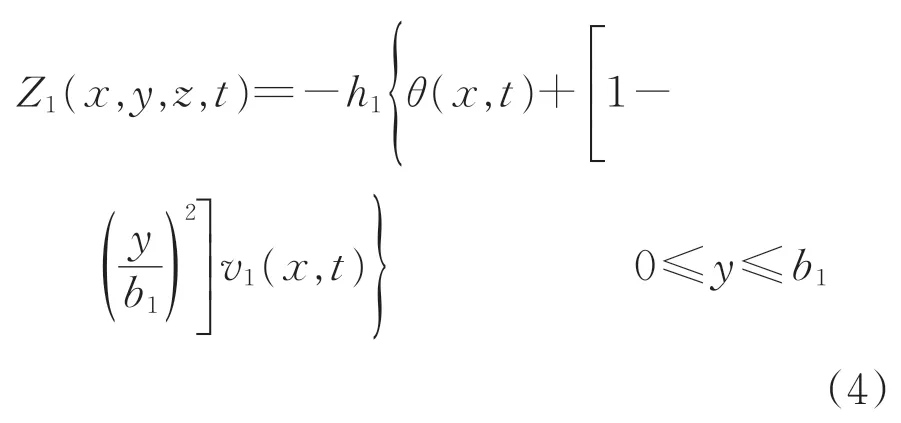
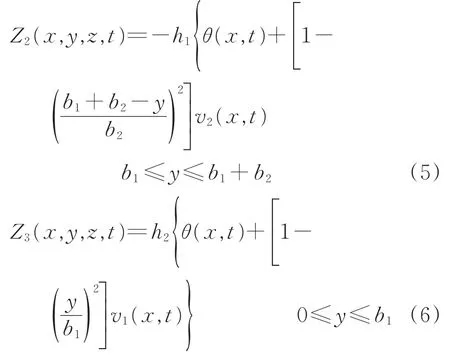
式中:v1(x,t)为自由振动时顶、底板的纵向动位移差函数;v2(x,t)为自由振动时悬臂板的纵向动位移差函数;θ(x,t)为箱形截面相对于y轴的竖向动转角。
顶板、悬臂板以及底板的应变能Uk为
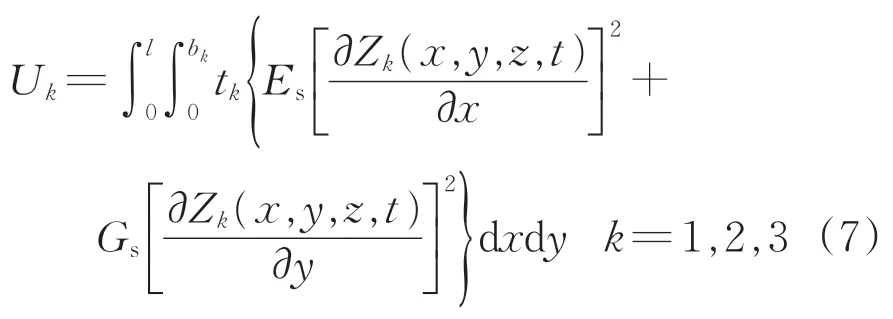
式中:Gs为钢材剪切模量。
组合箱梁振动时的外力势能Up为
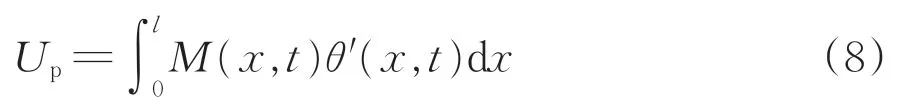
式中:M(x,t)为x截面的动弯矩。
波纹钢腹板剪切应变能Uf为
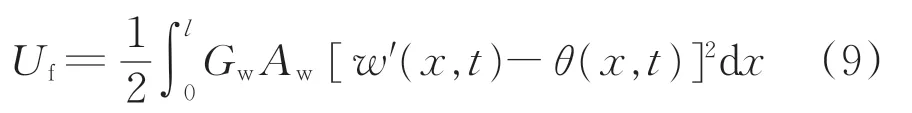
式中:Aw为波形钢腹板的横截面积。
组合箱梁总势能U为

结构总动能T为
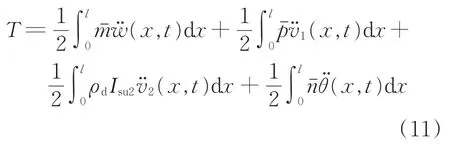
其中,
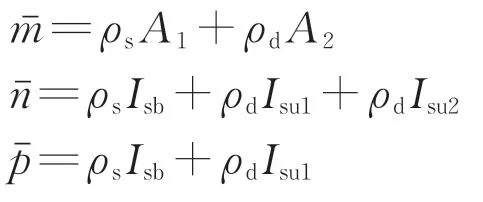
式中:A1和A2分别为U 形钢槽和等效钢顶板的横截面积;Isu1,Isu2和Isb分别为组合箱梁顶板、悬臂板和底板对中性轴的惯性矩;ρs为钢材的质量密度。
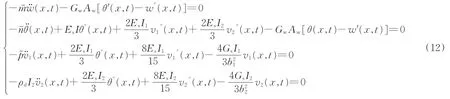
式中:I 为组合箱梁上下翼板对中性轴的惯性矩;I1为组合箱梁顶板和底板对中性轴的惯性矩;I2为组合箱梁悬臂板对中性轴的惯性矩;字母上的“·”表示对时间求偏导;字母上的“'”“″”表示对x求偏导。
同理,可得组合箱梁自然边界条件方程为
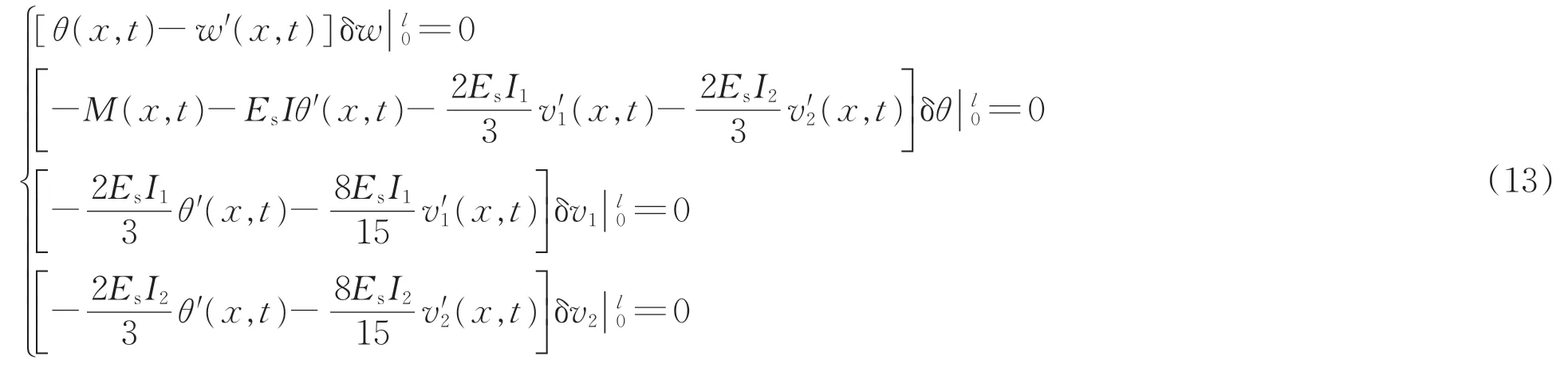
根据组合箱梁的自由振动特点,令
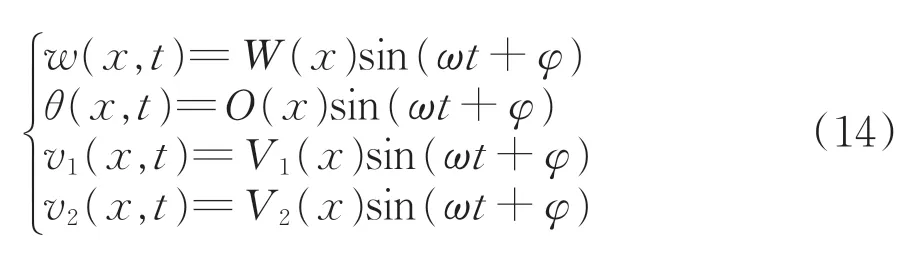
式中:W(x)为竖向挠度的广义位移函数;Ο(x)为竖向动转角的广义位移函数;V1(x)为顶、底板纵向位移差函数的广义位移函数;V2(x)为悬臂板纵向位移差函数的广义位移函数;ω 和φ 分别为组合箱梁自由振动的圆频率和初始相位角。
将式(14)代入式(12)后整理可得
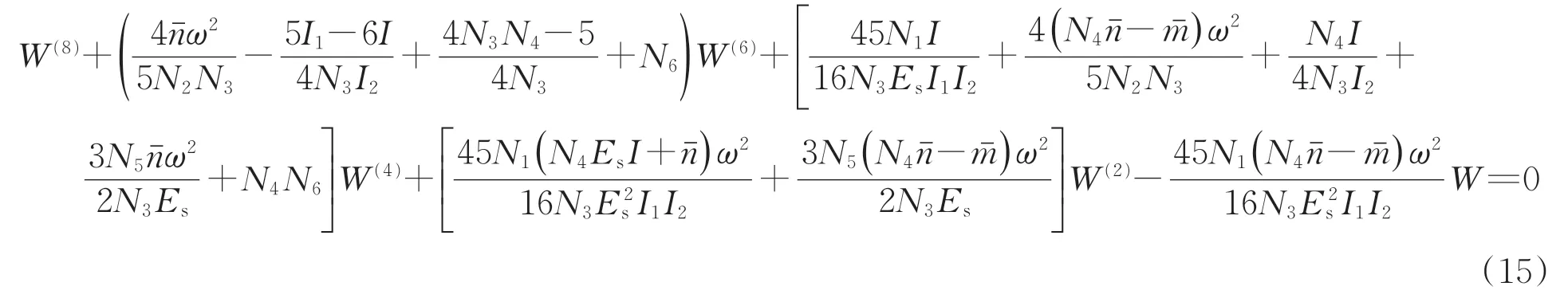
其中,
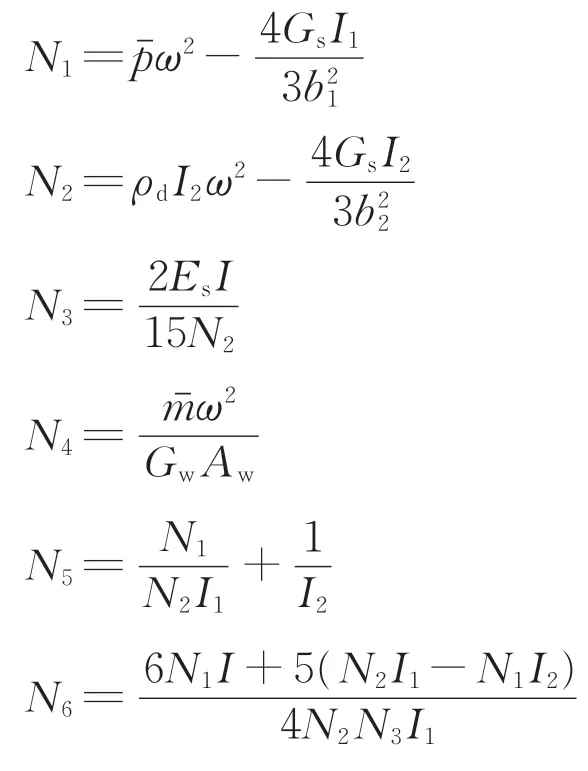
对式(15)求解可知,其特征方程的解为
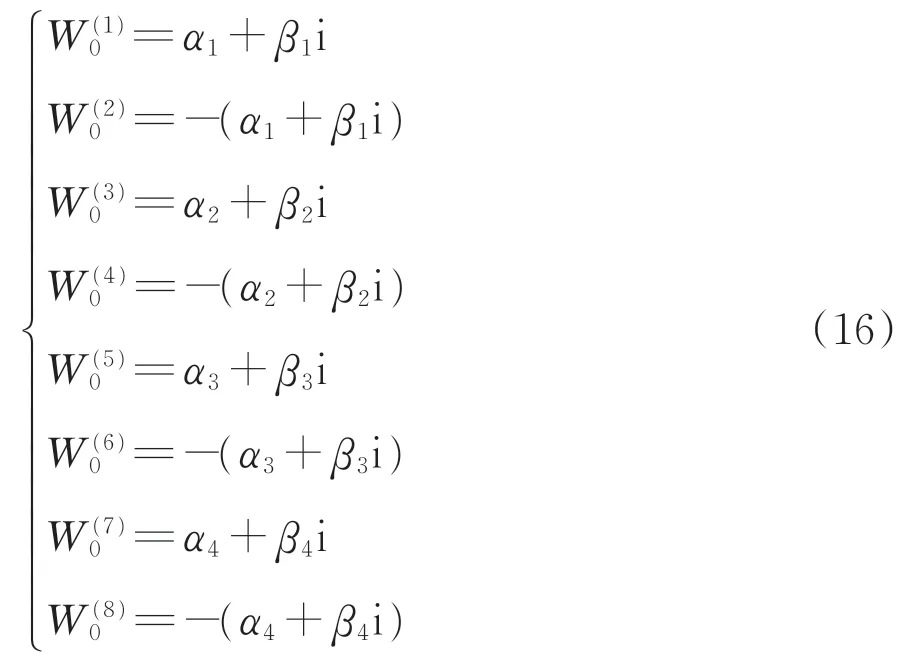
式中:α1,α2,α3和α4为解的实部;β1,β2,β3和β4为解的虚部。
根据微分方程的性质,可得式(15)的解为
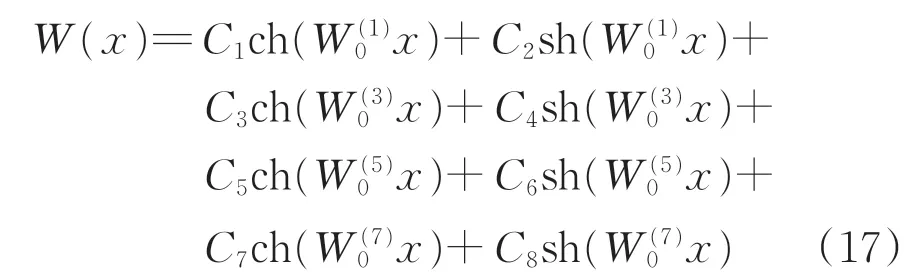
式中:C1—C8为积分待定常数,由相应边界条件确定。
由常微分方程组性质和恒等式原理,最终得到Ο(x)和Vj(x)(j=1,2)的解为
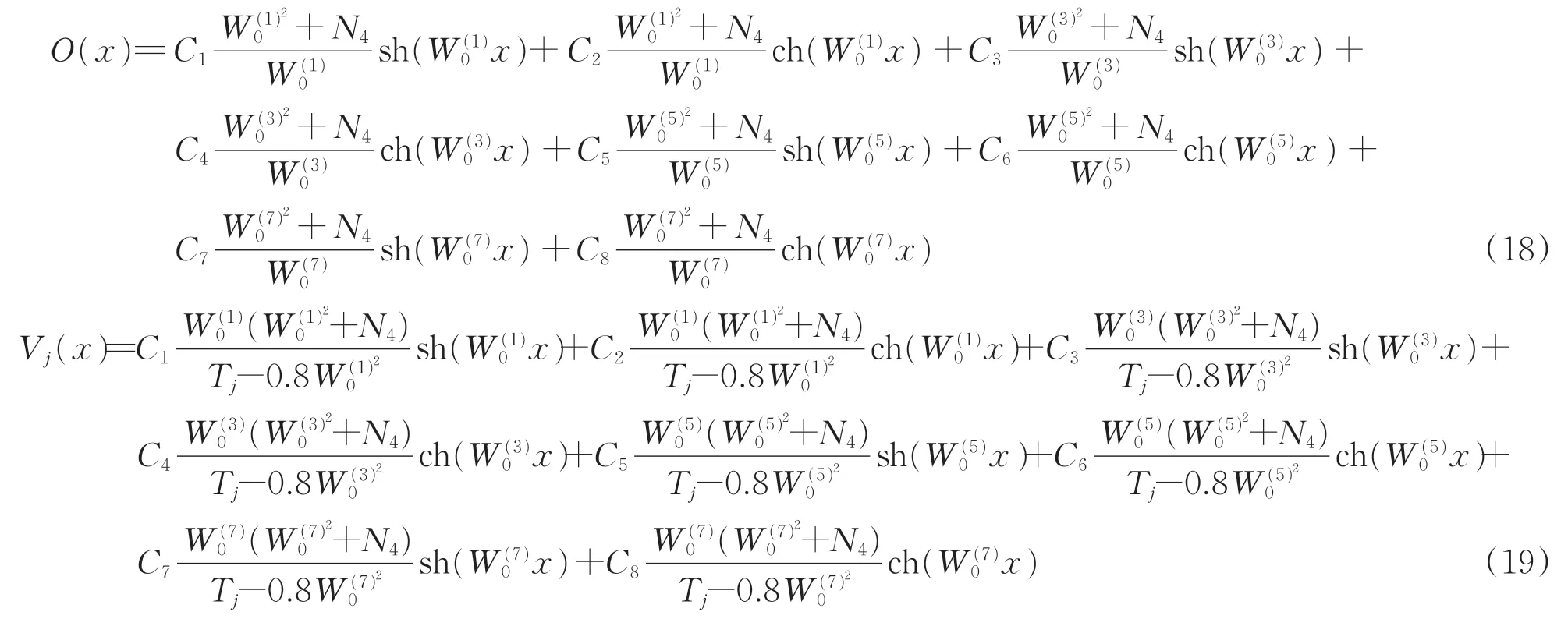
其中,
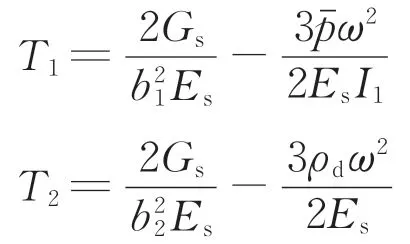
如图3 所示的等截面连续组合箱梁,若n 跨连续组合箱梁的跨距分别为l1,···,li,···,ln,且每跨的刚度和质量分布均匀,则有
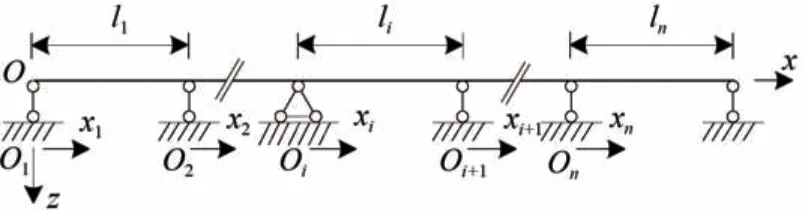
图3 等截面连续组合箱梁
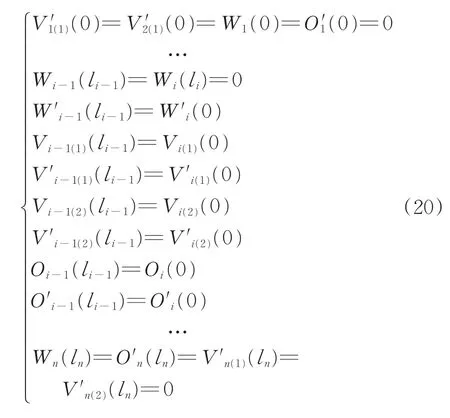
式中:Vi-1(1)(x)为第i-1 跨的组合箱梁顶、底板纵向位移差函数的广义位移函数;Vi-1(2)(x)为第i-1 跨的组合箱梁悬臂板纵向位移差函数的广义位移函数。
将W(x),Ο(x),V1(x)和V2(x)及其求导式代入连续梁边界条件得到关于积分待定常数的特征矩阵方程

式中:δn为对应边界条件下积分待定常数矩阵;Bn为与积分待定常数相对应的关于ω的函数矩阵。
式(21)要有非零解,由于δn不恒为零,则要|Bn|=0,利用MATLAB软件对其行列式求解,即可得到连续组合箱梁对应各阶竖向振动的圆频率。
波纹腹板钢箱组合连续梁竖向振动的圆频率ω转化成竖向振动频率f的计算式为

2 验 证
2.1 模型梁试验
为验证本文波纹腹板钢箱组合连续梁振动方程及其闭合解的有效性,设计制作了2 跨等截面波纹腹板钢箱组合连续梁模型,其横截面形状如图1所示。梁高0.45 m,跨径为(3+3) m,b1=0.3 m,b2=0.25 m,t1=0.05 m,t2=4 mm。组合箱梁顶板混凝土材料按照C50混凝土设计,波形钢腹板和底板均采用Q345 钢,共设置了2 道端横隔板和5道中横隔板,模型试验梁如图4所示。波纹钢腹板厚度为3 mm,波纹钢腹板构造示意图如图5所示。

图4 模型试验梁立面布置图(单位:cm)
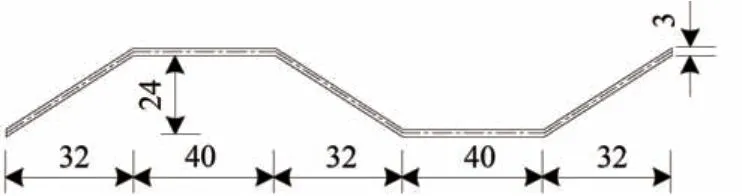
图5 模型试验梁(单位:mm)
采用瞬态激振法对连续组合梁自振特性进行测试,在冲击锤端部配置不同硬度的锤头进行锤击,冲击力锤与锤击点的接触时间不同,其范围为0.001~0.005 s。采样频率为512 Hz。为避免所关心频率的丢失,冲击荷载的位置根据结构的振型确定,应避免敲击点设置在结构前几阶模态振型的结点上。根据本试验模型振型的计算分析结果,竖向拾振器及激振点布置如图6所示。
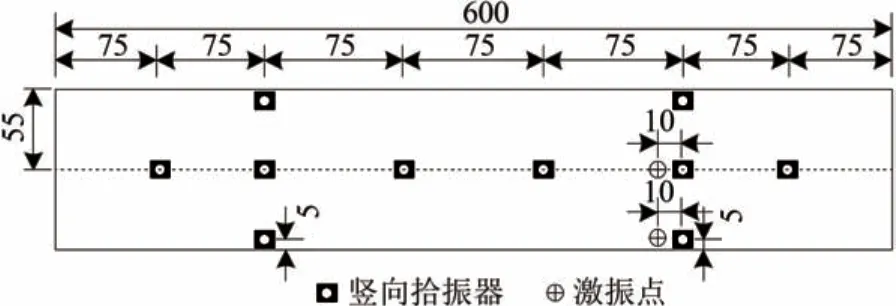
图6 模型试验梁竖向拾振器及激振点布置图(单位:cm)
试验中保持激励位置不变,调节量程范围,使用适当的敲击力在激励位置进行多次敲击,利用DH5922 动态信号采集仪采集测点位置的加速度响应信号,通过东华DHDAS信号测试分析系统进行FFT 谱分析后得到试验梁的自振特性,模型试验梁动力测试图如图7所示。

图7 模型试验梁动力测试图
2.2 模型梁的有限元模型建立
采用有限元分析软件ANSYS 建立波纹腹板钢箱组合连续梁有限元模型[16],如图8 所示,其中混凝土顶板及横隔板采用SOLID65 单元模拟,波纹钢腹板和钢底板选用SHELL63 单元模拟,波形钢腹板和混凝土板的连接利用MPC(Multipoint Constraints)技术进行处理,波纹钢腹板和钢底板的连接利用布尔操作的GLUE 命令粘接;波纹腹板钢箱组合连续梁有限元模型的边界条件为:模型2 端采用活动铰支座,即对2 端钢箱最底下的1 排节点的Y和Z方向位移进行约束;中间采用固定铰支座,即对中间钢箱最底下的一排节点的X,Y 和Z方向位移进行约束。

图8 组合箱梁有限元模型
2.3 结果对比
波纹腹板钢箱组合连续梁的频率测试结果如图9 所示。运用本文闭合解计算该连续组合箱梁前4 阶竖向弯曲振动频率f1,所得结果与铁摩辛柯梁理论解f2、有限元解f3和模型试验值f4进行对比,由于ANSYS 模型中钢板选用SHELL63单元模拟,在计算竖向弯曲频率中高阶振型夹杂了钢板局部振动的因素,根据有限元分析结果,选取局部振动影响较小的前3 阶组合箱梁竖向频率,对比结果见表1。
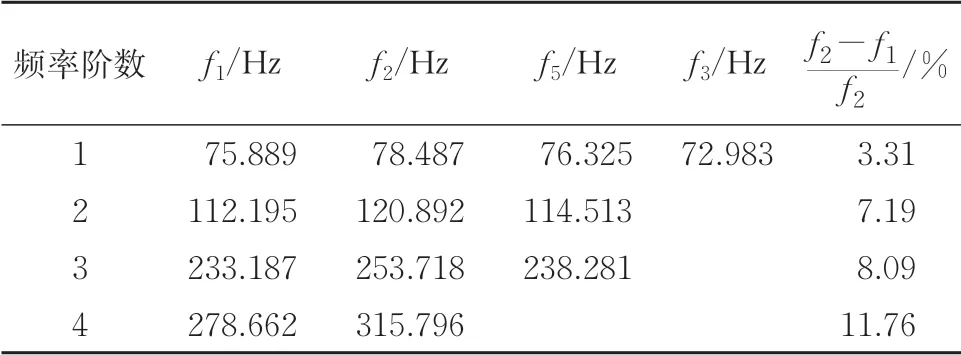
表1 连续组合箱梁振动频率对比
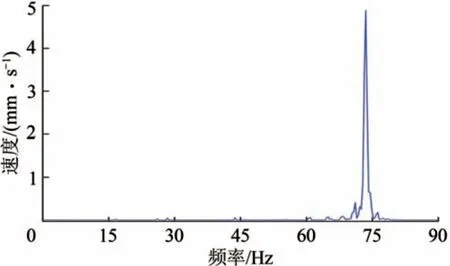
图9 频率测试结果
从表1 可以看出:本文闭合解计算所得2 跨连续组合箱梁弯曲振动频率与有限元计算结果与实测值吻合较好,说明本文振动方程及其闭合解的建立是正确性,考虑剪力滞效应影响后组合箱梁竖向各阶固有频率值皆呈减小趋势,且对高阶频率影响较大,连续组合箱梁第4 阶频率的剪力滞贡献达11.76%,因而在计算此类结构高阶频率时剪力滞效应不可忽略。
为进一步验证采用换算截面法分析波纹腹板钢箱组合连续梁桥自振特性的可行性,将文中模型试验组合梁的钢底板按照等刚度法换算为混凝土板,利用本文闭合解结合其他方法计算波纹腹板钢箱组合连续梁与传统波纹钢腹板组合连续梁(底板为混凝土板)的自振频率和模态,计算结果见表2。
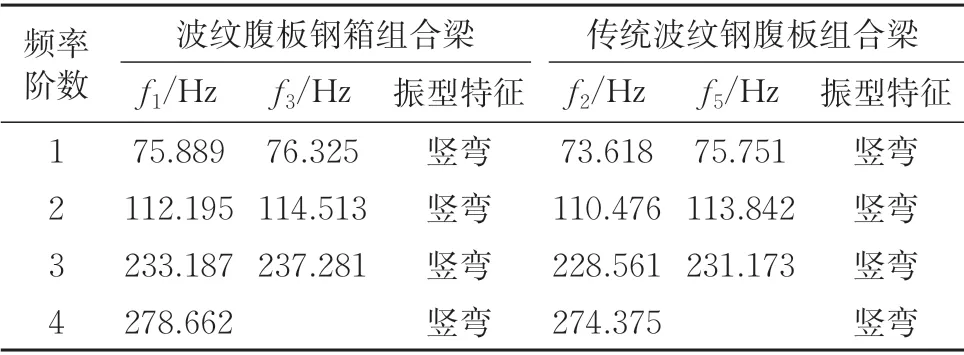
表2 2种波纹腹板组合连续梁竖向自振特性对比
从表2 可以看出:按照等刚度法得到的传统波纹钢腹板组合连续梁与波纹腹板钢箱组合连续梁竖向振型特征完全一致,但其各阶频率值均小于波纹腹板钢箱组合连续梁,这主要是由于刚度相同时,采用混凝土底板的组合箱梁质量大于钢底板组合箱梁,因而相应自振频率也会减小,说明采用换算截面法分析波纹腹板钢箱组合连续梁桥的自振特性在理论上是可行的。
3 等截面波纹腹板钢箱组合连续梁的自振特性影响
3.1 宽跨比
为研究宽跨比(2b1/l)对波纹腹板钢箱组合连续梁桥自振特性的影响,选取上述2 跨连续组合箱梁模型,控制其他结构参数不变,当跨径l 分别取2,3(模型尺寸),4 和5 m 时,对应的宽跨比(2b1/l)分别为0.30,0.20,0.15,0.12。按照本文理论及铁摩辛柯梁理论计算模型梁前4阶竖向弯曲振动频率f1和f2随宽跨比的变化情况,结果如图10所示。
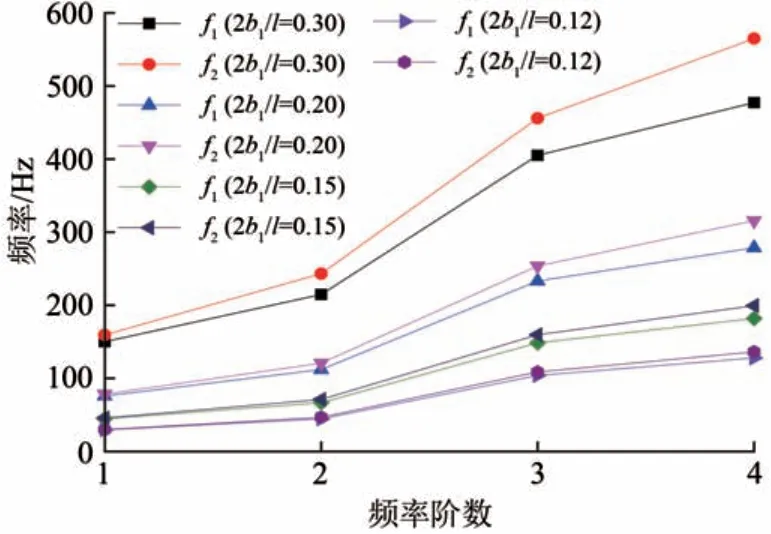
图10 2跨连续组合箱梁在不同宽跨比下的频率对比
从图10 可以看出:剪力滞效应对连续组合箱梁各阶频率的影响随宽跨比(2b1/l)的增大而变大,当宽跨比2b1/l=0.30 时,组合箱梁1~4 阶竖向自振频率的差值比由5.48%增至15.54%,说明剪力滞效应对其自振频率的影响随阶数的升高而趋强;当2b1/l 在0.12~0.30 时,仅考虑剪切变形的铁摩幸柯理论与本文理论方法所得组合箱梁基频结果基本一致,最大误差为5.84%,说明此时在实际工程中计算其竖向基频时直接采用铁摩幸柯理论即可。
3.2 褶皱效应
考虑褶皱效应对组合箱梁自振特性的影响,将如图1 所示组合箱梁的波纹腹板变为等厚度的平钢腹板,其他结构尺寸不变,运用本文理论计算不同腹板类型组合箱梁的自振频率,结果见表3。表中:fp为平钢腹板组合箱梁频率值;fb为波纹腹板组合箱梁频率值;η为褶皱效应。
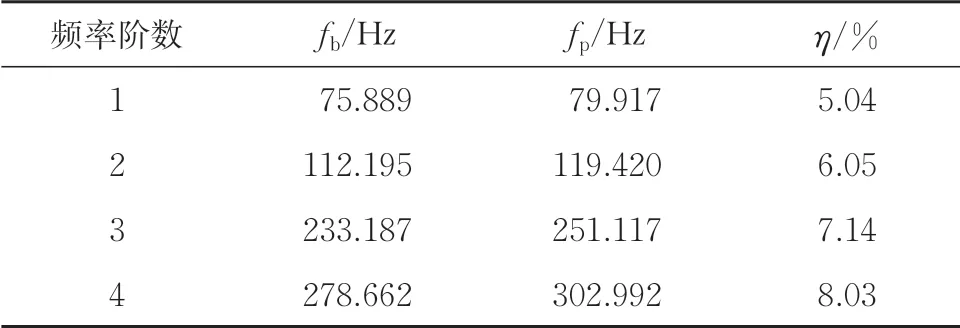
表3 褶皱效应对连续组合箱梁振动频率的影响
褶皱效应的计算式为

从表3 可以看出:波纹腹板组合箱梁前4 阶竖向振动频率均小于平钢腹板组合箱梁,1 阶—4 阶竖向自振频率的褶皱效应由5.04%增至8.03%,说明受褶皱效应的影响,波纹腹板组合箱梁的竖向刚度减小,且频率阶数越高,褶皱效应的影响越大。
3.3 钢底板厚度
以本文制作的2 跨连续组合箱梁为例,控制其他结构参数及跨度不变,分别将其钢底板的厚度取为2,3,4 模型尺寸),5,6,7 和8 mm,按照本文理论计算前4阶竖向自振频率值随钢底板厚度的变化情况,结果如图11所示。
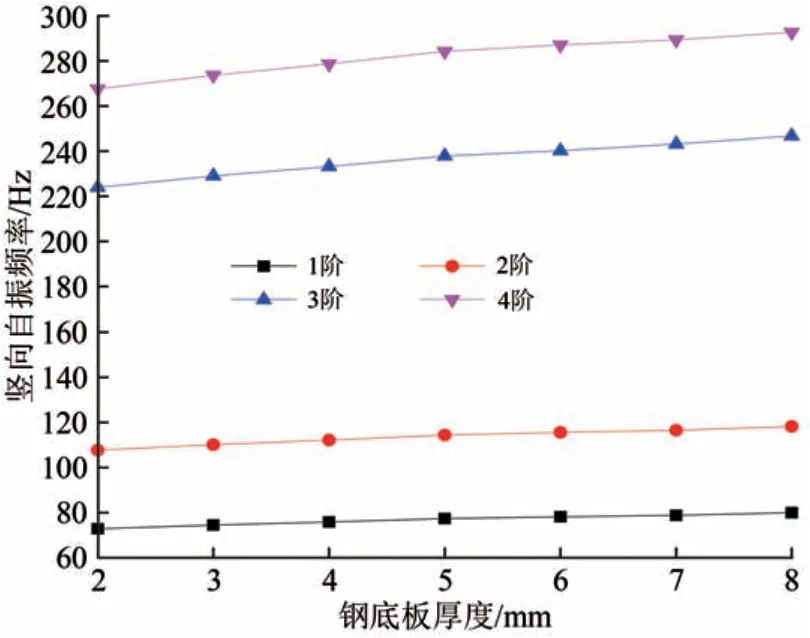
图11 连续组合箱梁振动频率随钢底板厚度变化
从图11可以看出:增加钢底板厚度,2跨连续组合箱梁各阶频率值逐渐增大,说明增加钢底板厚度有利于提升结构整体刚度,底板厚度从2 mm 增至8 mm 时,结构前4 阶频率依次增大了11.34%,10.27%,10.02%,9.83%,9.66%,9.32% 和8.78%。由此可见底板厚度的变化对2 跨连续组合箱梁1阶频率的影响较大,对其高阶频率的影响趋势减弱,所以工程实际中应结合经济性合理选择钢底板厚度,以改善组合桥梁自振特性。
4 本文解析法与现行规范比较
根据规范[18]中关于连续梁桥竖向基频的规定,当计算连续梁的冲击力引起的正弯矩效应时,基频f11估算公式为
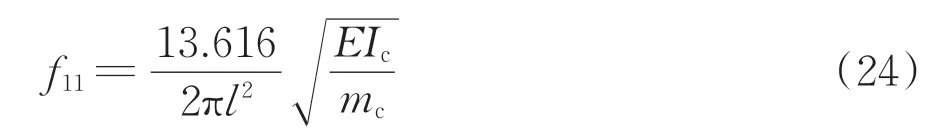
当计算连续梁的冲击力引起的负弯矩效应时,基频f22估算公式为

式中:E 为结构材料的弹性模量;Ic为结构跨中截面的截面惯性距;mc为结构跨中处的单位长度质量。
以本文制作的2 跨连续组合箱梁为例,采用式(24)和式(25)分别计算其基频f11和f22,并将计算结果与本文解析法所得频率f1进行对比,结果见表4。

表4 连续组合箱梁竖向基频对比Hz
从表4 可以看出:采用规范公式计算2 跨连续组合箱梁基频与本文理论计算的基频相差较大,差值分别为57.69%和173.91%,显然,用规范公式计算波纹腹板钢箱组合连续梁的自振频率偏大,但这样计算所得的冲击效应也会偏大,对于桥梁设计将偏于安全。
5 结 论
(1)以能量变分法和Hamilton 原理为基础,提出一种能够准确分析波纹腹板钢箱组合连续梁自振特性的解析法,计算结果与模型试验值和有限元数值解吻合良好,进而验证了本文方法的准确性。
(2)按照等刚度法得到的传统波纹钢腹板PC组合连续梁与波纹腹板钢箱组合连续梁竖向振型特征完全一致,但其各阶频率值均小于波纹腹板钢箱组合连续梁,表明采用换算截面法计算波纹腹板钢箱组合连续梁的自振特性在理论上是可行的。
(3)忽略剪力滞效应时,波纹腹板钢箱组合连续梁各阶频率值普遍较大,说明剪力滞效应降低了组合箱梁的竖向刚度,随着频率阶数升高,剪力滞效应的影响增大;剪力滞效应对连续组合箱梁自振频率的影响随宽跨比的增大而变大,实际工程中当组合箱梁宽跨比在0.12~0.30 时,可直接采用铁摩幸柯理论计算其竖向基频。
(4)受褶皱效应的影响,波纹腹板钢箱组合连续梁的自振频率减小,且阶数越高,褶皱效应的影响越大;底板厚度的增加对2 跨连续组合箱梁1 阶频率的影响较大,对其高阶频率的影响趋势减弱;采用规范公式计算波纹腹板钢箱组合连续梁的自振频率将偏于安全。
