基于主导模态的高速铁路矮塔斜拉桥易损性地震动强度参数研究

2021-08-12谢明志杨永清黄胜前李晓斌

中国铁道科学 2021年4期

谢明志，杨永清，黄胜前，洪彧，李晓斌，庄重

（1.西南交通大学土木工程学院，四川成都 610031；2.成都建工集团有限公司，四川成都 610000）

合理地震动强度参数的选取是进行桥梁易损性分析的基础，不同地震动参数在量化与评估不同体系桥梁结构损伤时存在差异［1］。当前对于评估结构地震损伤尚不存在唯一最优地震动强度参数，因此从区域抗震、防灾减灾而言，研究地震动强度参数与结构损伤相关性，并针对不同桥型选择合适的地震动强度参数进行损伤评估具有理论及实践意义。

国内外学者对进行桥梁易损性分析的地震动参数选取做了相关研究。吕大刚等［2］基于多元统计学，以单自由度体系为研究对象，将地震动加速度、地震动速度及地震动位移等相关的地震动参数拟合成1 个综合指标，分析结构损伤与参数相关性时，得出考虑多参数相关性的强度参数优于单一地震动参数。LI L F 等［3］以1 座主跨380 m 的4 塔斜拉桥为例，对“地震波峰值型”“反应谱峰值型”及“特定周期谱值型”等9种常见地震动强度参数进行分析，指出常规地震动强度参数在进行此类型桥梁易损性评估时不适用，宜采用特定周期谱加速度。钟剑等［4］以1 座（156+430+156）m 公路混合梁斜拉桥为背景，对比地震动峰值加速度（PGA），峰值速度（PGV），1 阶周期对应的加速度反应谱（Sa，T1），0.2 s周期对应的加速度反应谱（Sa，0.2），1.0 s 周期对应的加速度反应谱（Sa，1.0）几个参数在概率地震需求分析时的特点，认为峰值加速度（PGA）是最为合理的指标。Padgett 等［5］指出，对于公路桥梁抗震计算，PGA 较为合理。武芳文等［6］采用谱加速度对1座主跨565 m 的混合梁斜拉桥索塔进行易损性分析，Xuewei Wang等［7］采用峰值加速度（PGA）对1座公铁两用的大跨斜拉桥进行损伤及倒塌分析，得到构件损伤超越概率，进行风险性评估。庞于涛等［8］研究峰值速度（PGV）、持续最大速度（SMV）、反应谱速度峰值、Housner 强度、1 s 周期对应谱参数及Arias 强度与桥梁损伤的相关性，得出对于大跨刚构桥不同参数分析的差异性。申彦利等［9］指出考虑高阶模态的地震动参数对高墩抗震性能分析和评价具有很好的可行性。对于地震动强度参数的研究，当前较侧重于公路斜拉桥。高速铁路斜拉桥一方面静力特性与常规大跨斜拉桥存在差异［10-12］，另一方面，地震作用下桥梁动力响应及行车安全性异于公路桥［13-15］，采用不同的地震动强度参数，进行量化与评估桥梁损伤时存在差异。桥梁结构易损性分析较依赖于地震动强度参数，合理选择地震动强度参数需充分考虑地震动频谱及结构自振特性。

本文以怀邵衡铁路沅江大桥（90+180+90）m的矮塔斜拉桥为研究对象，进行适用于高速铁路矮塔斜拉桥易损性评估的基于主导模态的地震动强度参数研究。

1 基于桥梁主导模态的地震动强度参数

1.1 桥梁主导模态

矮塔斜拉桥在顺桥向地震动作用下桥梁的动力平衡方程为

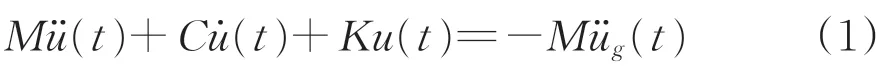
式中：M 为桥梁结构质量矩阵；C为桥梁结构阻尼矩阵；K 为桥梁结构刚度矩阵；(t)，和u(t)分别为桥梁结构相对加速度、速度和位移矢量；t)为地震动在顺桥向加速度。

根据模态叠加法，式（1）可分解为

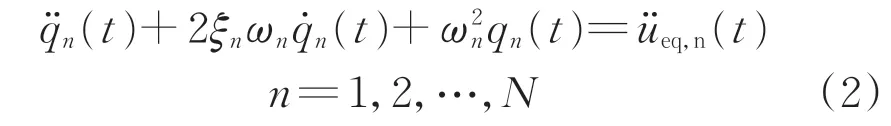
式中：qn(t)为结构第n阶模态广义坐标；ξn为阻尼比；ωn为第n阶振型的圆频率；(t)为第n阶模态对应的广义加速度时程；N为计算模态的总数。

由式（2）求解第n 阶振型的结构位移u(t)向量为

式中：Φ为结构模态矩阵。

桥梁在某一瞬时总应变能为

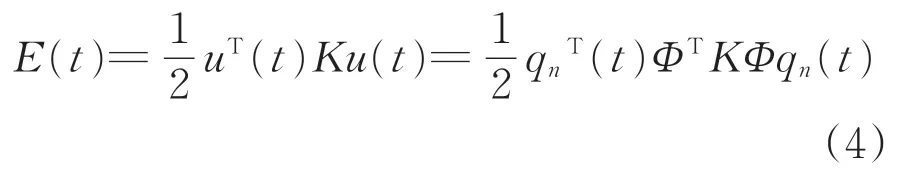
结构第n阶模态的广义刚度矩阵Kn与广义质量矩阵Mn满足

因此，桥梁总的平均振型应变能可定义为

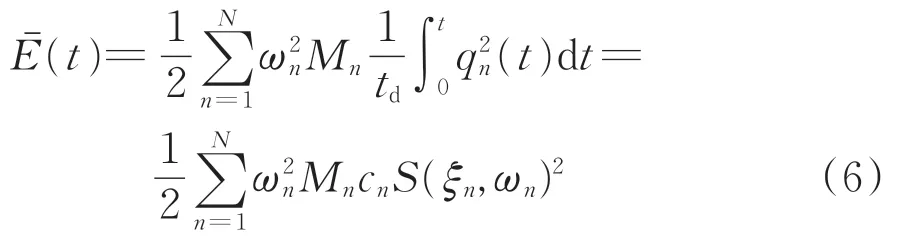
式中：cn是与桥梁第n 阶振型圆频率与地震动持时t相关的系数，根据经验及相关资料这里取3［16-17］；S(ξn，ωn)为加速度时程对应的位移谱。由此可得第n阶平均振型应变能为

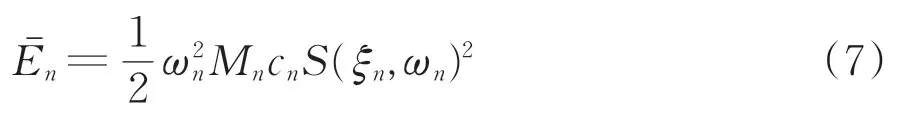
可见，平均振型能量系数不仅能反映桥梁自振特性，也包含了地震动频谱信息，同时也反映了第n 阶模态对结构总模态的贡献，参数值越大，对应模态的贡献越大。因此，对该参数数值的选取和定义是判断桥梁各振型贡献的重要阈值。

对于处于一定设防烈度、抗震等级、区域场地的桥梁结构，定义在地震作用下贡献较大的模态为“主导模态”。

1.2 基于主导模态的地震动强度参数

采用平均振型能量系数进行矮塔斜拉桥主导模态识别，能同时考虑地震动与结构特性，针对在一定的场地、地形地貌的桥梁结构，对于定量分析结构地震响应具有重要的理论及现实意义。在此基础上，针对桥梁体系特点，构造式（8）所示的基于桥梁主导模态的地震动强度参数Sa，gui为

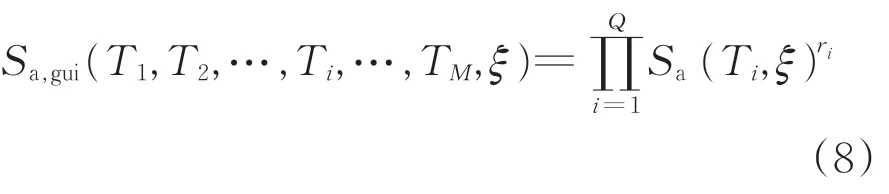
式中：Ti为桥梁结构第i 阶主导模态对应的周期；Q 为主导模态个数；ξ 为桥梁结构阻尼比；Sa(Ti，ξ)为第i 阶主导模态对应的地震动加速度反应谱值；ri为第i 阶主导模态对应的平均振型能量系数。

对式（8）两端取自然对数得

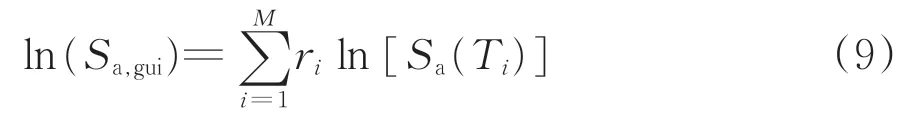
该地震动强度参数求解时，首先采用平均振型能量系数计算结构主导模态；然后计算各主导模态的自振周期Ti，找到该主导模态周期下的Sa(Ti)，计算对应的平均振型能量系数ri；最后由式（9）计算。

2 计算模型及地震波选取

2.1 工程概况

以湖南怀邵衡铁路沅江矮塔斜拉桥为背景，其为跨径（90+180+90）m 的双线铁路单箱单室预应力混凝土矮塔斜拉加劲连续梁桥。本桥桥面宽13.6 m，梁底宽9.4 m，中支点梁高9.6 m，跨中梁高5 m，梁底变高处按二次抛物线变化。索塔为C55钢筋混凝土双柱矩形塔，塔高28 m。斜拉索为空间双索面，采用抗拉强度为1 860 MPa 钢绞线，共56 根拉索。主梁为C55 混凝土，二期恒载115 KN·m-1。桥墩采用C35钢筋混凝土，墩号为10#—13#，其高度分别为22.9，20.35，21.85 和11.35 m，均为圆端形截面。桩基础采用C35 钢筋混凝土钻孔灌注桩。活动及固定支座采用球形钢支座，该桥总体布置及截面信息如图1所示。

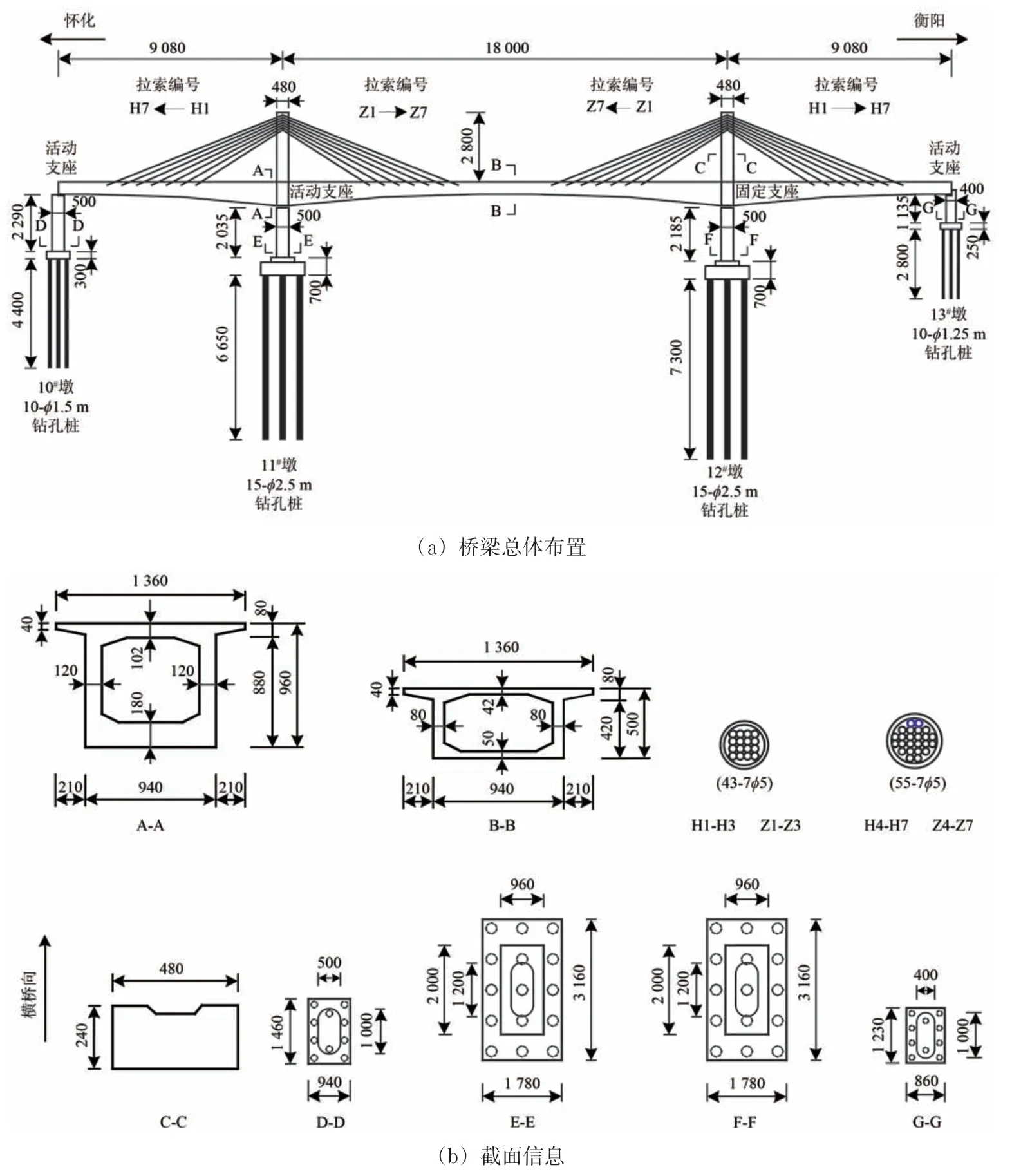
图1 矮塔斜拉桥总体布置及截面信息（单位：cm）

索塔配筋如图2 所示。索塔配筋均采用HRB400钢筋，除点筋采用直径25 mm 钢筋，其余均采用16 mm 钢筋。桥墩配筋布置如图3 和表1 所示。桥墩配筋除点筋采用直径16 mm HRB400钢筋外，其余均采用直径10 mm HPB300钢筋。

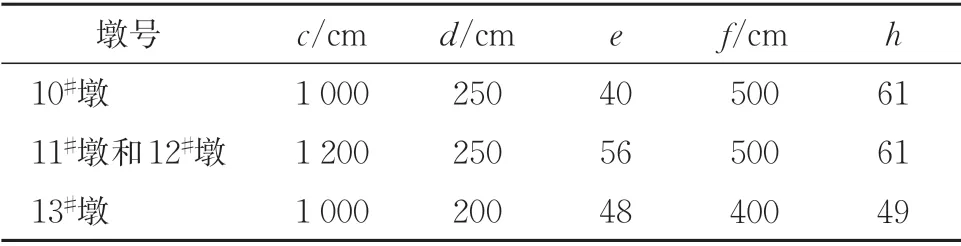
表1 10#—13#墩截面尺寸及配筋信息

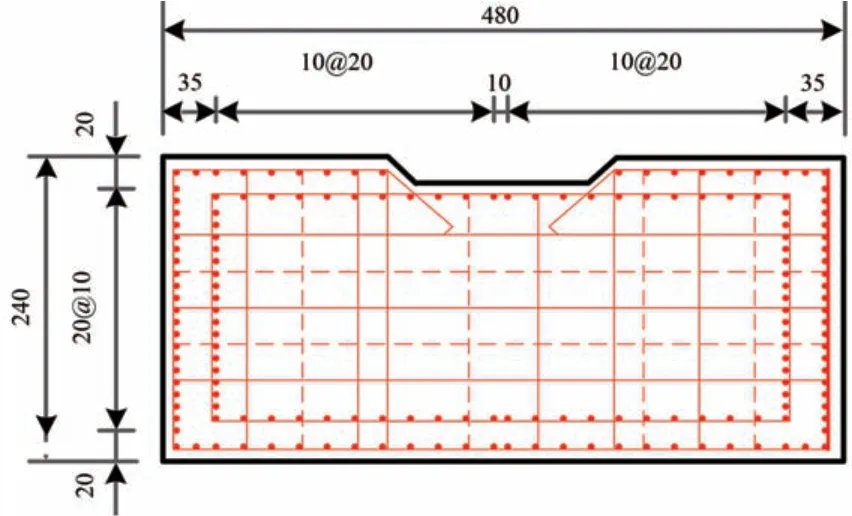
图2 索塔配筋布置图（单位：cm）

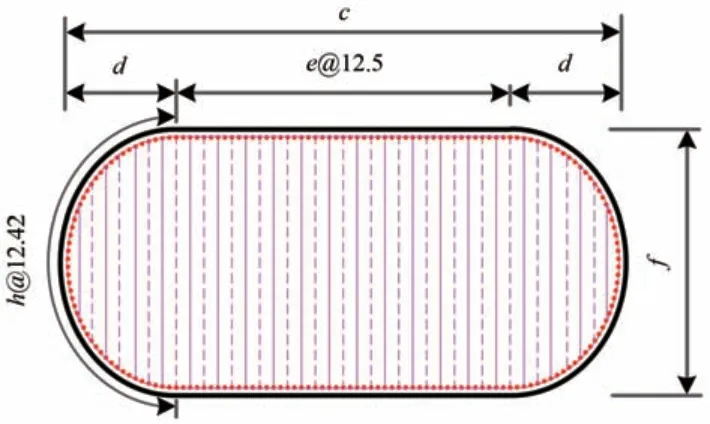
图3 桥墩配筋布置图（单位：cm）

2.2 非线性有限元模型

本桥采用OpenSees 开源程序建立非线性有限元模型。斜拉索采用桁架单元模拟，主梁采用弹性梁柱单元模拟，索塔、桥墩和桩基础均采用非线性梁柱单元模拟，支座采用零长度单元模拟；桩土效应采用土弹簧模拟，采用零长度单元；本桥构件间的连接刚臂采用弹性梁柱单元模拟。对于结构材料选取，斜拉索采用Steel02，主梁采用弹性材料，索塔、桥墩和桩基材料采用Concrete02 和Steel02，支座采用弹塑性材料，土弹簧和刚臂均采用弹性材料。

支座滞回模型如图4所示。图中：Fcr为滑动临界力；kp为支座滑移后的刚度；k0为支座滑移前的刚度。混凝土及钢材本构关系分别如图5 和图6 所示。图中：f'cc为约束混凝土峰值抗压强度；εcc为f'cc对应的应变；fcc为约束混凝土极限抗压强度；εcu为fcc对应的应变；f'c0为非约束混凝土峰值抗压强度；εc0为f'c0对应的压应变；fc0为非约束混凝土极限抗压强度；ε'cu为fc0对应的压应变；εsp为非约束混凝土剥落应变；Esec为约束混凝土割线模量；Ec为非约束混凝土弹性模量；fy为钢筋应力，E 为钢筋弹性模量。

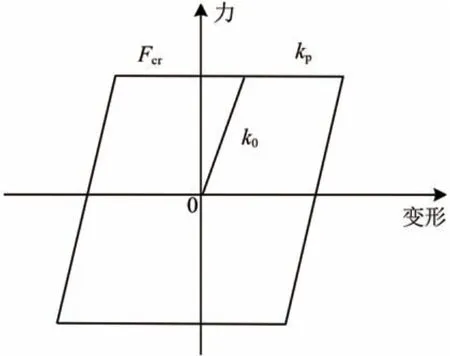
图4 球形支座滞回模型

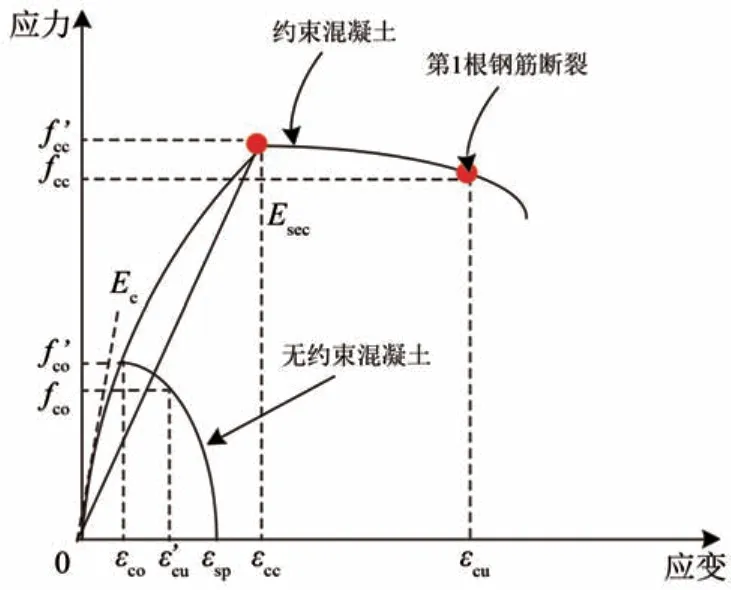
图5 混凝土本构关系

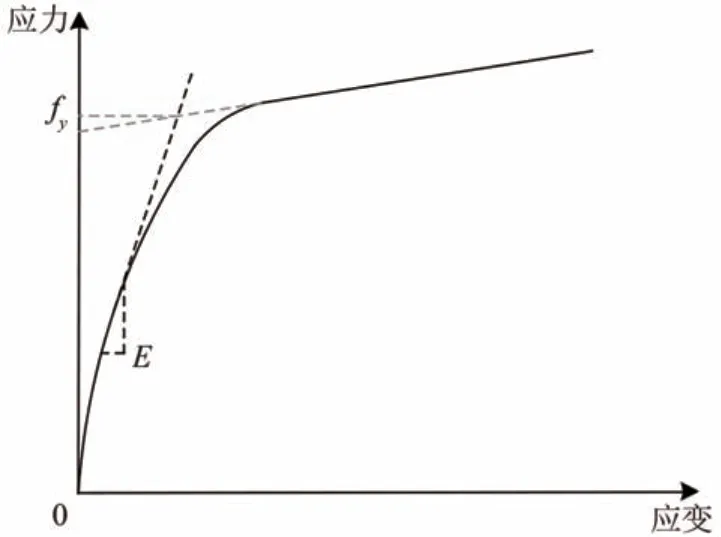
图6 钢筋本构关系

土弹簧刚度采用“m”法计算，沿桩长方向划分等代土层厚度，施加在每根桩节点处。每一土层土弹簧刚度k按下式计算。

式中：a 为计算土弹簧刚度的等代土层厚度；b 为桩基计算宽度；m 为地基系数的比例系数；z 为土层计算深度。

以10#墩为例，沿桩长方向，每层土按2 m 考虑，即a=2，共划分23层；顺桥向宽度为1.85 m，横桥向宽度为1.54 m，顺、横桥向的m 值均取为20 221.0 kN·m-4。计算得到的横桥向及顺桥向土弹簧刚度见表2。

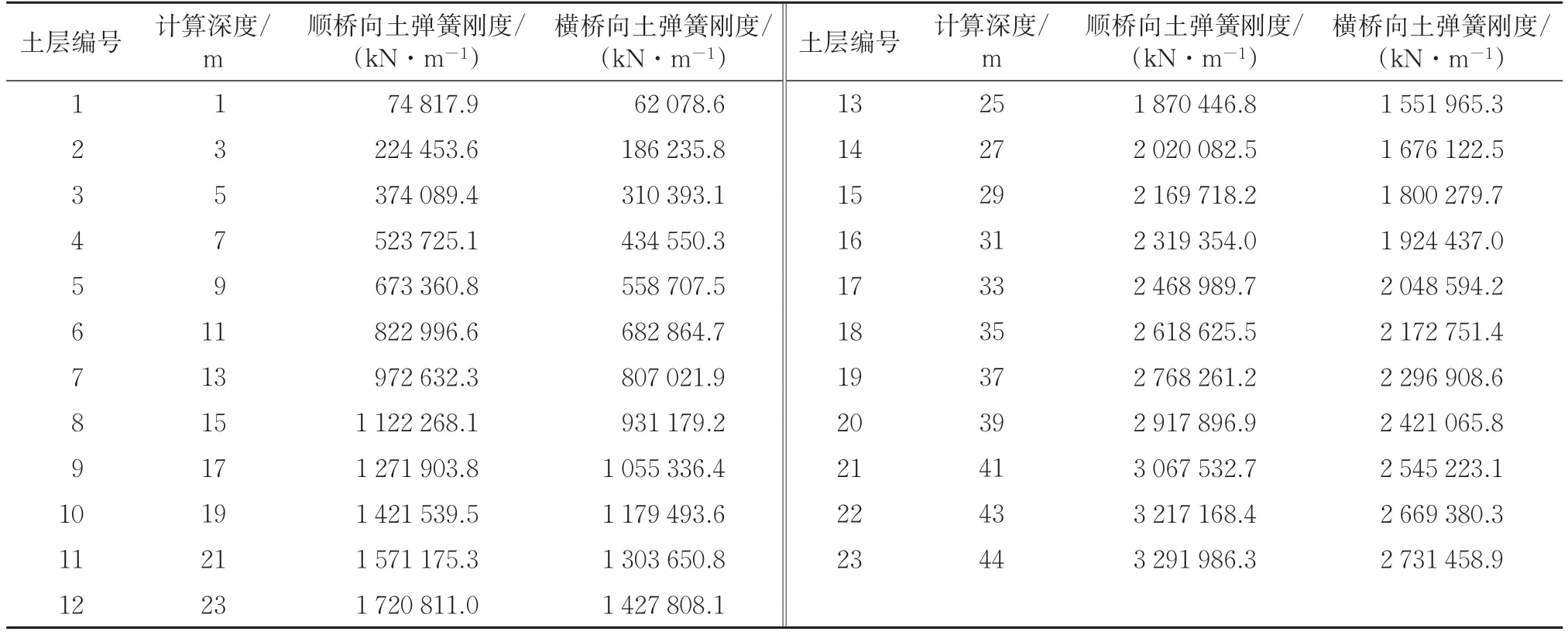
表2 10#墩土弹簧刚度

全桥三维有限元模型如图7所示。

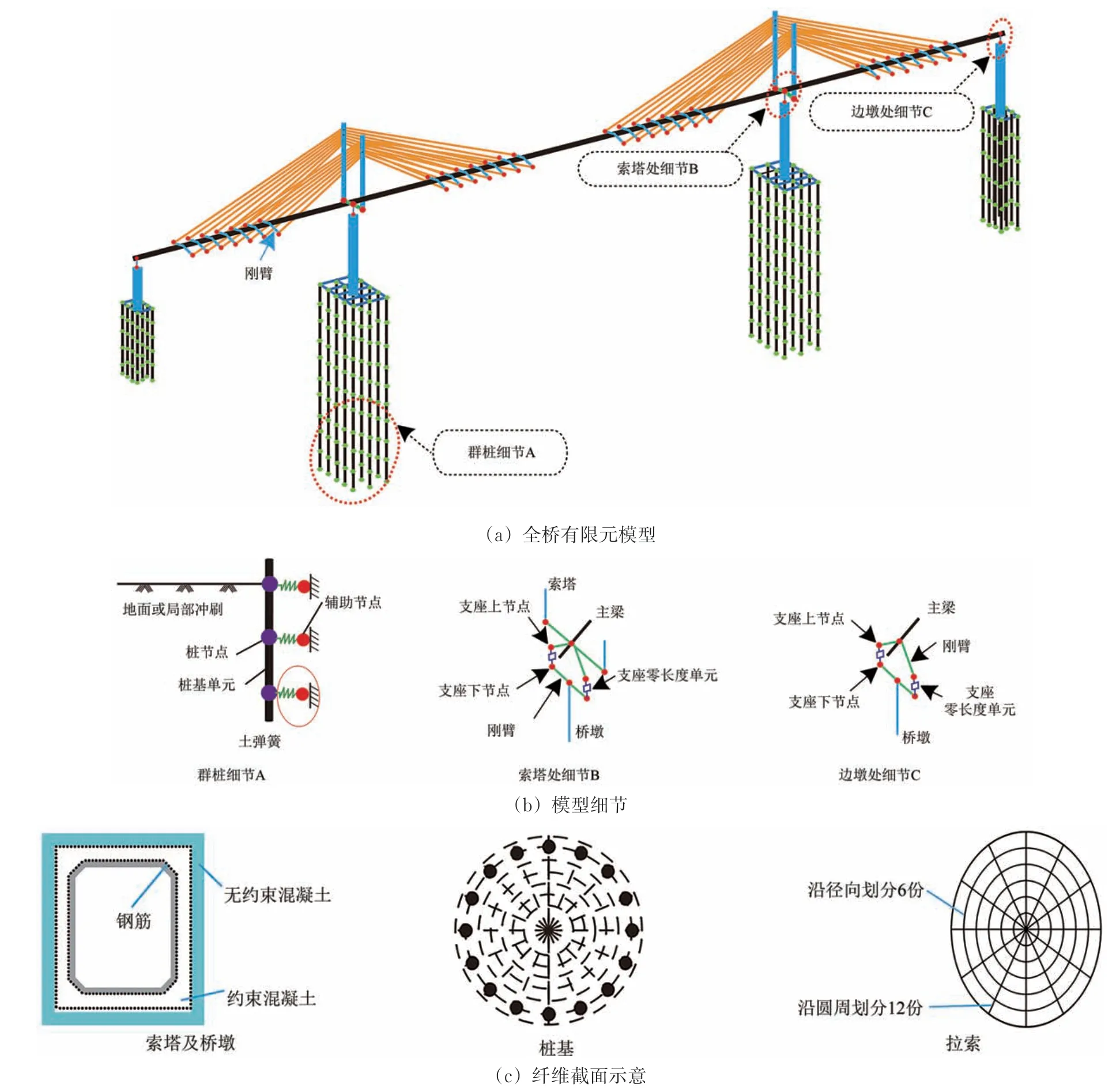
图7 非线性有限元模型

本桥混凝土容重取26.5 kN·m-3，主梁混凝土弹性模量取36 GPa，斜拉索弹性模量取195 GPa，屈服强度取1 860 MPa，支座摩擦系数取0.02，阻尼比取0.05，钢筋屈服强度为400 MPa，钢筋弹性模量为200 GPa。

索塔、桥墩及桩基混凝土参数见表3。

表3 索塔、桥墩及桩基混凝土参数

2.3 地震波选取

根据本桥所处位置及地质条件，按II类场地考虑。考虑到地震动不确定性，选取的地震波需有一定的数量。综上所述，本文从美国太平洋地震工程研究中心（PEER），以均方差最小原则［18］选取30条地震波，顺桥向加速度反应谱如图8所示。

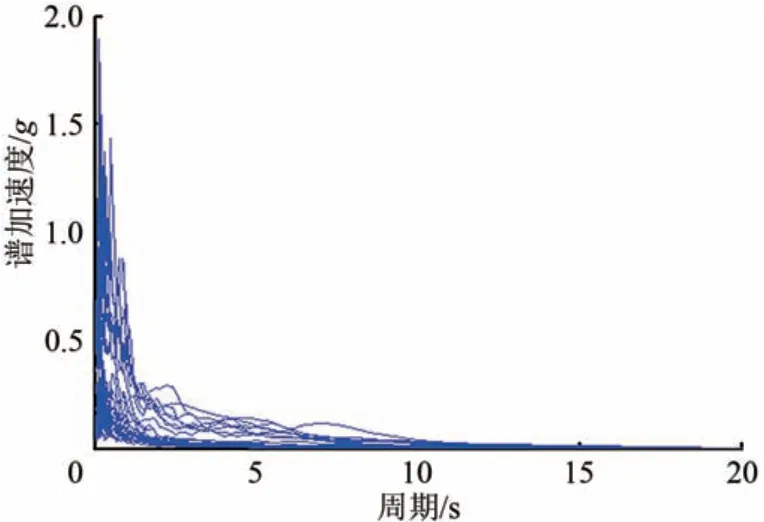
图8 顺桥向加速度反应谱

3 矮塔斜拉桥地震动强度参数评估

3.1 基于矮塔斜拉桥主导模态的地震动参数计算

首先通过平均振型能量系数识别矮塔斜拉桥主导模态，然后根据式（9）计算Sa，gui。本文将rn的阈值设定为0.01，识别主导模态。rn大于或等于0.01 对应的模态为矮塔斜拉桥主导模态，即计算Sa，gui时需要考虑的模态。以编号“RSN1838”地震波为例，顺桥向地震动下，本桥的主导模态和平均振型能量系数计算结果见表4，由此根据式（9）得到的对应地震动强度参数为0.054 8g。同理，计算得到对应30 条地震动的该桥地震动强度参数见表5。

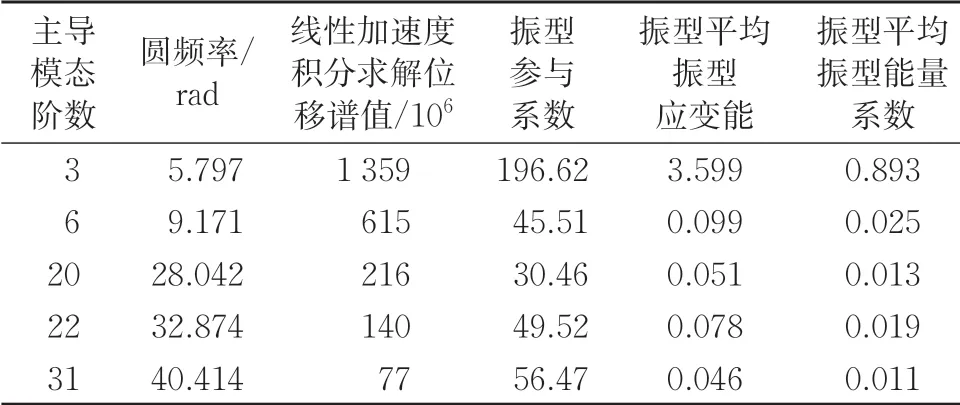
表4 “RSN1838”地震波下该桥主导模态及平均振型能量系数

表5 各地震波下该桥基于主导模态的地震动强度参数

3.2 地震动强度参数评估

结合文献中常采用的地震动强度参数［4，19］，根据高速铁路矮塔斜拉桥力学特点，本文选取PGA，PGV，地震动位移峰值PGD，地震动加速度反应谱峰值Sa，max，地震动速度反应谱峰值Sv，max，地震动位移反应谱峰值Sd，max，地震动1 阶加速度反应谱Sa，T1以及Sa，gui进行时程分析，根据分析结果，从“相关性”“高效性”“充分性”进行综合评估，得出适用于该类型桥梁易损性分析的地震强度参数。

进行地震动参数的评估，首先需选择能反映结构损伤状态的响应参数，这是建立二者映射关系的基础。从结构易损性工程需求参数中，选择的响应参数需综合考虑结构承载性能及功能特性。

本文选择索塔底部弯矩屈服曲率、支座位移、桥墩弯矩屈服曲率、墩顶位移、主梁梁端转角及斜拉索索力共6 个工程需求参数（EDPs）。地震需求参数D和地震动强度参数IM满足如下关系。

式中：A和B均为回归系数；ε为误差。

将式（11）两边取自然对数可得：

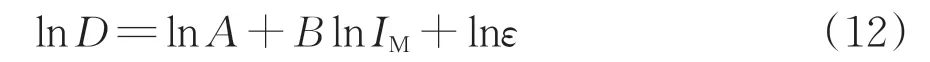
式（12）中lnD 服从正态分布。本文采用增量动力分析（IDA），对PGA 调幅处理，从0.1g 调至1.5g，对矮塔斜拉桥进行动力时程分析，并通过式（12）将式（11）的计算结果取自然对数，然后将这些数据回归分析，对上述地震动强度参数进行综合评价。

3.2.1 相关性

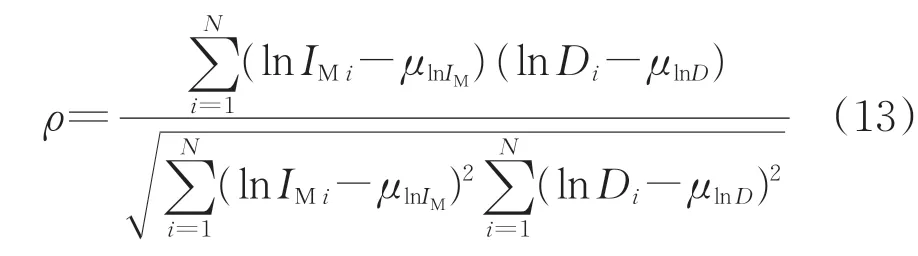
“相关性”可采用皮尔森相关系数ρ（Pearson Correlation Coefficient）评估，其表达式为式中：μlnIM和μlnD分别为地震动强度和需求参数的均值；N 为动力时程分析得到的（Di，IMi）数据对个数。

皮尔森系数ρ 越小，说明lnIM和lnD 的相关性弱，反之相关性强。

以过渡墩10#墩墩顶位移u为例，分别对8个地震动强度参数和响应进行回归分析，结果如图9和表6 所示。图9 中：aPGA，vPGV和uPGD分别为PGA，PGV和PGD的值。

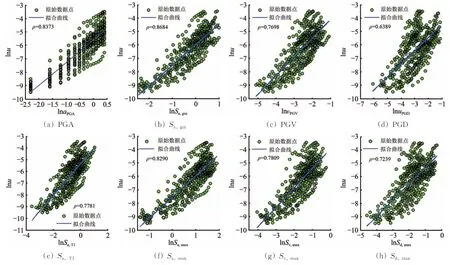
图9 10#墩墩顶位移与8个地震动强度参数对数回归曲线

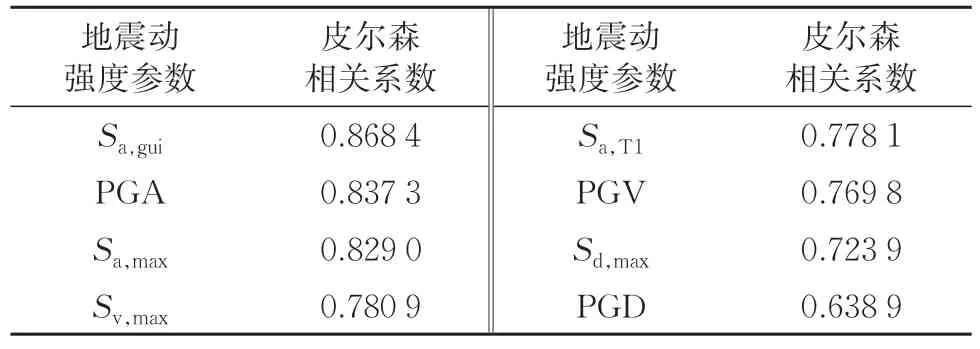
表6 10#墩墩顶位移地震动强度参数相关性系数

结果表明，对于10#墩墩顶位移，Sa，gui相关系数最大为0.868 4，其次为PGA，其ρ值为0.837 3，Sa，max的ρ 值为0.829，PGD 的相关系数最小为0.638 9。

地震动强度参数与各工程需求参数相关性分析如图10所示。

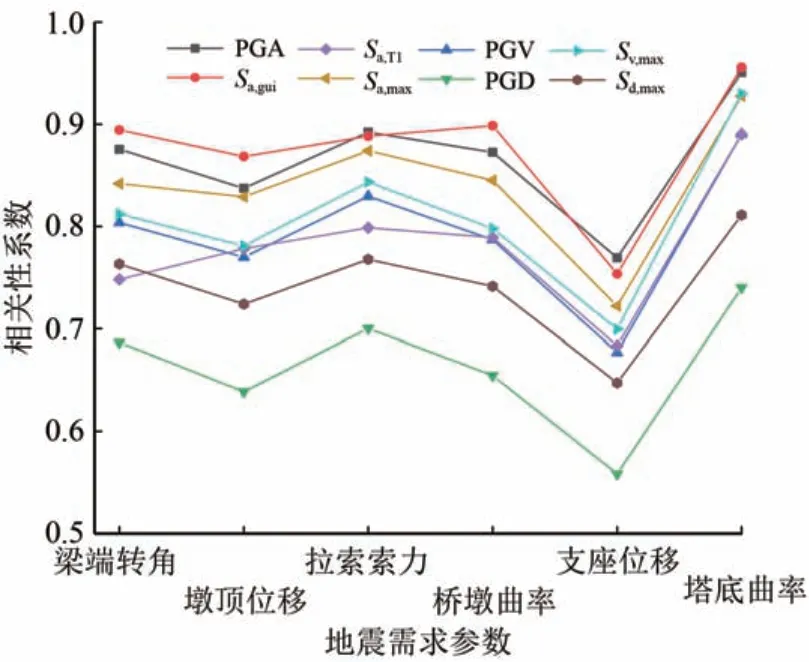
图10 相关性分析对比

从图10 可看出：对于拉索索力和支座位移，PGA 的相关性系数虽最大，但与Sa，gui相关性系数的差异较小。对于其余工程需求参数，相关性系数最大的是Sa，gui，其次是PGA，Sa，max和Sa，gui，说明考虑地震动频谱和结构自振特性的地震动强度参数与结构变形响应的相关性最大；梁端转角、墩顶位移、拉索索力及受压构件（索塔和桥墩）曲率这几个工程需求参数总体与8个地震动强度参数的相关性系数均较大，均在0.8 以上，相关性非常好；拉索索力虽然与地震动强度参数的相关性系数较大，但拉索索力的变化量相对较小，对于刚度较大的高速铁路矮塔斜拉桥，地震作用下索力变化率相对其他需求参数敏感性较小。

3.2.2 高效性

“高效性”指概率地震需求模型（PSDM）中，变异系数较小，反映了IM 和D 之间的离散性。该参数可用结构在第i 个地震作用下的峰值响应Di和A（IM）B的对数关系表达式为

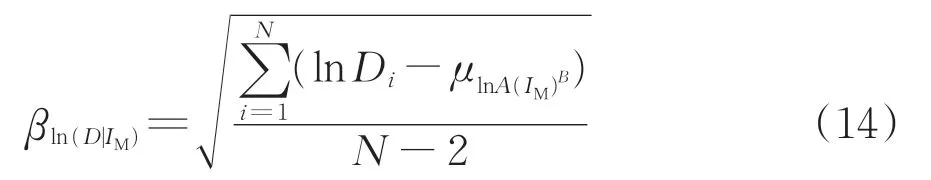
βln(D|IM)越大表明地震动强度参数高效性越弱，反之则越好。高效性分析结果如图11所示。

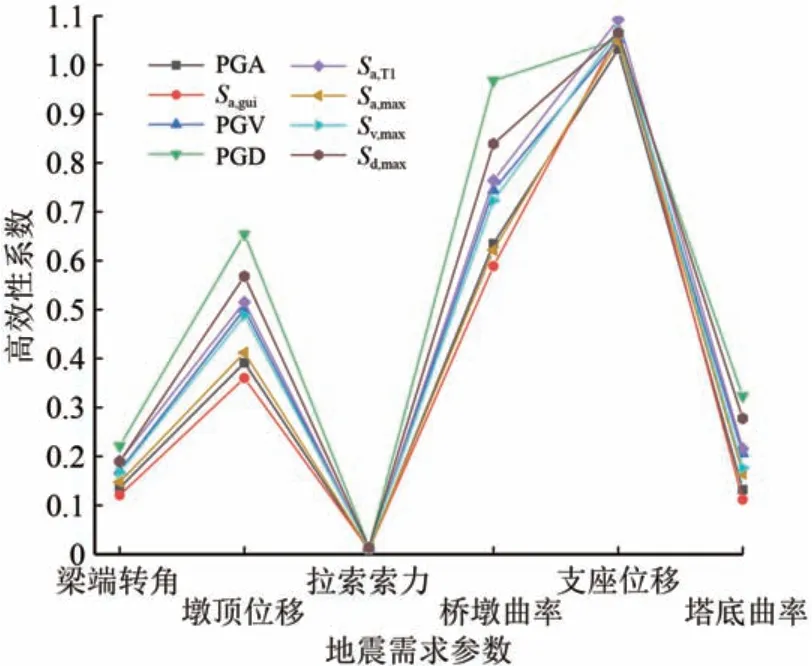
图11 高效性分析对比

对于拉索索力和支座位移，其PGA 对应的βln(D|IM)最小，分别为0.01 和1.03，对于其余工程需求参数，Sa，gui对应的βln(D|IM)值最小。

从图10 和图11 可得出，地震动参数与工程需求参数相关性越强，其离散性越弱，即变异性越小。对于拉索索力，各地震动强度参数与其离散性最低，也进一步说明对于该体系桥梁，地震动作用下对拉索的总体影响较弱。

3.2.3 充分性

“充分性”反映了地震动强度参数IM与地震动特性如矩震级、断层距等的关联性，是评估参数合理与否的重要指标，也是概率地震需求分析的基础。具备充分性的IM，在计算桥梁损伤概率时，应不受其他参数对地震需求模型的影响。地震动强度参数“充分性”的判断，可对式（12）的误差项lnε或断层距进行回归分析，如式（15）所示。

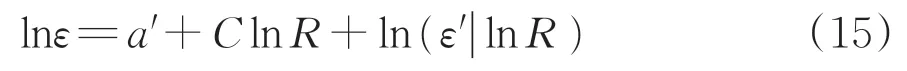
反映地震动参数的充分性用参数P表示，本文P 的临界值取0.05［16-17］，大于该值，充分性越强，反之充分性越弱。地震动强度参数与各工程需求参数充分性分析结果如图12所示。

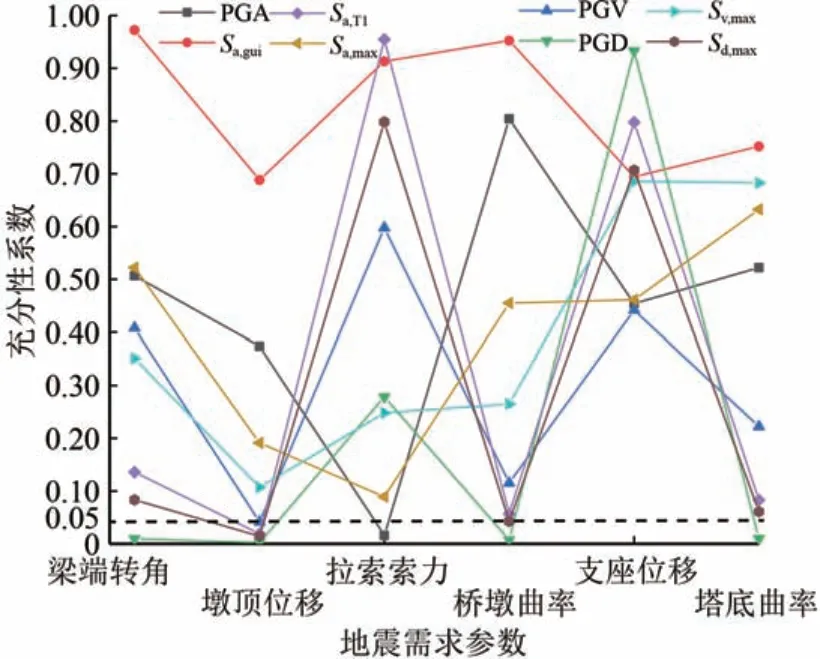
图12 充分性分析对比

从图12 可见：对于拉索索力，Sa，T1的P 值最大为0.80，对于支座位移，PGD 的P 值最大为0.93，对于其余需求参数，Sa，gui对应的P 值均最大，反映该参数对其他事件的依赖性越低，具有较强的合理性。对于梁端转角的PGD，墩顶位移的PGV，PGD，Sa，T1和Sd，max，拉索索力的PGA，桥墩曲率的PGD 和Sd，max，索塔底曲率的PGD，P值均小于0.05，充分性较弱。

综上分析，针对高速铁路矮塔斜拉桥地震损伤，采用基于主导模态的地震动参数Sa，gui具有较强的相关性、高效性和充分性。