多年冻土区路基填筑短期内冻土温度场数值分析
2021-08-12王蕴嘉郭惠芹叶阳升王仲锦王鹏程张千里
王蕴嘉,郭惠芹,叶阳升,王仲锦,王鹏程,张千里
(1.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081;2.中国铁道科学研究院研究生部,北京 100081;3.中国铁道科学研究院集团有限公司,北京 100081)
我国青藏高原的平均海拔超过4 500 m,其中近70%的面积被多年冻土覆盖[1-2]。多年冻土是一种对温度变化非常敏感的特殊土体,其物理力学性质与土体温度密切相关。在多年冻土上进行路基修建等活动,势必会打破冻土与环境间原有的能量动态平衡,改变冻土场的热状态,进而影响路基等构筑物的稳定性[3-6]。青藏铁路穿越多年冻土区路段长达632 km,在建的川藏铁路同样面临多年冻土问题。基于此,开展多年冻土区路基填筑对冻土温度场影响的相关研究对保证两路的顺利修建和安全运营具有重要意义。
现场监测和试验是研究路基填筑对冻土温度场影响的重要方法。王小军等[7]分析了11 个青藏铁路路基断面7 年监测数据,发现路基中心人为上限均随时间发展有所上升,有利于路基稳定;牛富俊等[8]调研了青藏铁路沿线55 个断面的监测结果,发现部分高温冻土区普通路基存在冻土上限下降、路基热稳定性差的情况,且工程施工对地表的热扰动、水热侵蚀易引发热融性灾害,产生路基沉陷等病害;穆彦虎等[9]分析了2005 年—2010 年间青藏铁路普通路基断面的地温监测数据,发现多年冻土区路基下冻土热稳定性与多年冻土平均地温密切相关,高温冻土区路基下部冻土热稳定性较差;张明礼等[10]研究发现,路基运营初期阳坡冻土上限下降,水的渗流不仅加速了路基的升温和变形过程,还加剧了路基温度场和水分场的非均匀性。此外,赵相卿等学者[11-12]也进行了相关研究。然而,现有研究大多关注的是路基填筑对多年冻土长期热稳定性的影响,而对路基填筑后短期内的温度场变化规律研究较少。且对短期内的冻结锋面下凹扭曲的监测存在一定难度。实际工程中,路基填筑热效应在短期内使得路基覆盖范围冻结锋面下凹扭曲,且在水分汇入充足的情况下还将引起持续性的下凹扭曲,产生路基热融沉降、路基开裂等病害,有必要对其进行深入研究。
近年来,大量学者采用数值模拟研究冻土工程相关问题,合理有效的冻土水热耦合模型则是数值研究的关键。Harlan[13]基于水分迁移理论提出了水热耦合的概念,首次建立了渗透系数与含冰量相关的水热耦合模型;徐学祖等[14]基于大量试验研究,给出了未冻水含量的经验公式;Liu 和Tian 等学者[15-16]以土体的状态焓为变量模拟分析相变潜热的影响;宋二祥等[17]基于Philip 等提出的非等温水热气耦合运移模型,提出综合考虑水力梯度和温度梯度影响的水气运移控制方程。此外,白清波等[18-19]也对冻土水热耦合模型进行修正和改进,并将其应用于数值模拟研究中。
基于冻土水热耦合计算控制方程,采用有限元软件COMSOL 提供的系数型偏微分方程模块(PDE)建立冻土水热耦合分析模型,进行路基填筑短期内冻土温度场的变化规律研究。
1 冻土水热耦合计算控制方程
1)水分场控制方程
冻结和融化土体中均含有一定量的未冻水。根据Philip 等[20]提出的非等温水热气耦合运移模型,水分迁移主要由水力梯度和温度梯度导致。参考文献[17]提出的水气运移控制方程,不考虑气态水的迁移,非饱和土中液态水迁移的控制方程可表示为
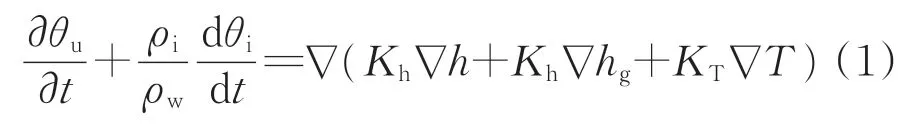
式中:θu和θi分别为未冻水和冰的体积分数;t 为时间,s;ρi为冰的密度,取900 kg·m-3;ρw为水的密度,取1 000 kg·m-3;Kh为等温条件下水力梯度导致的水力传导系数,m·s-1;KT为非等温条件下温度梯度导致的水力传递系数,m2·K-1·s-1;h 为基质吸力对应水头,m;hg为重力作用引起的水头,即位置水头,m;T 为绝对温度,K;∇为微分算子。
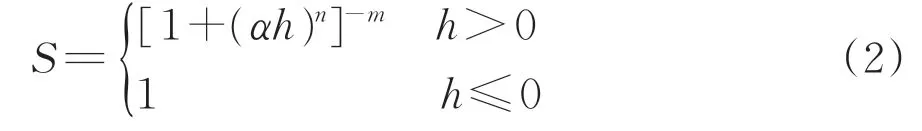
其中,
m=1-1/n
式中:α,n 和m 均为模型参数,需通过试验确定,α 单位为m-1;θs和θr分别为饱和体积含水率和残余体积含水率。
考虑冰水混合区冰对液态水迁移的阻碍作用,Kh可表示为
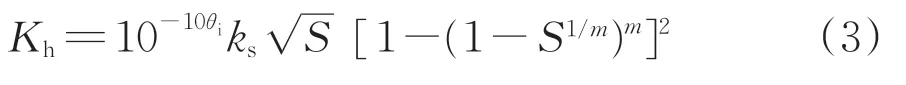
式中:ks为土的渗透系数。
非等温条件下温度梯度导致的水力传递系数KT的计算公式[21]为
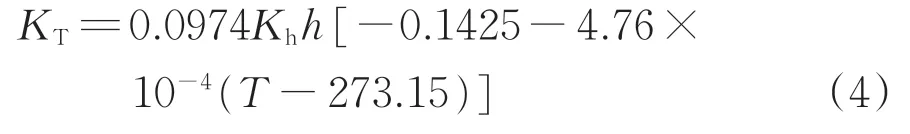
2)温度场控制方程
忽略土体冻结和融化过程中水分蒸发耗热等的影响,将冰水相变潜热视为热源,根据傅里叶定律,非饱和土瞬态温度场的控制方程可表示为
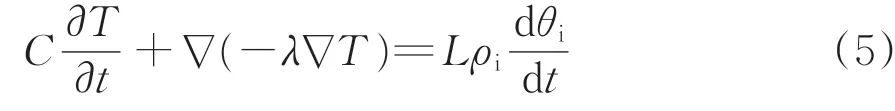
式中:C 为土的体积热容,J·(m3·K)-1;λ 为土的导热系数,W·m-1·K-1;L为冰水相变潜热,取334.5 kJ·kg-1。
冻土的体积热容和导热系数均由土骨架、未冻水、冰和孔隙气体共同决定。综合考虑计算效率和收敛性,本文仅针对土的冻融状态给定不同的热力学参数,即
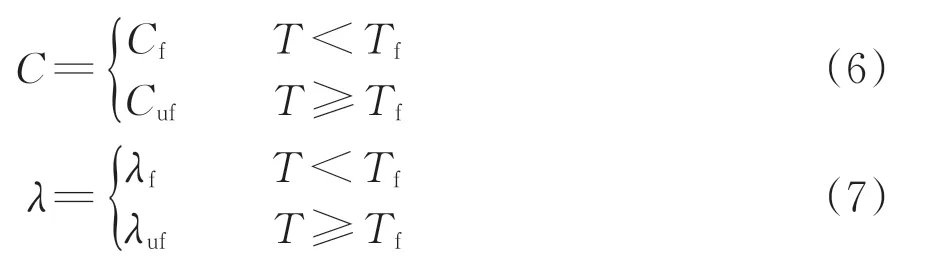
式中:Cf和Cuf分别为冻土和融土的体积热容,J·m-3·K-1;λf和λuf分别为冻土和融土的导热系数,W·m-1·K-1;Tf为土的冻结温度,K。
3)未冻水含量
水分场控制方程和温度场控制方程中共包含3 个未知量,分别为未冻水体积分数、冰体积分数和温度。若想求解水热耦合问题,仍需引入1个关于3个未知量的联系方程。
参考文献[19]未冻水含量可由下式计算。
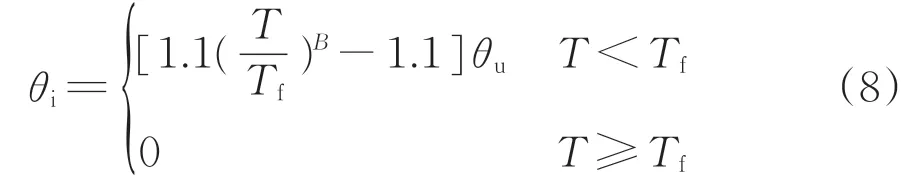
式中:B为经验参数。
2 冻土水热耦合计算控制方程验证
本文采用有限元软件COMSOL,模拟文献[14]中封闭条件下的土柱融化试验,进行验证冻土水热耦合计算控制方程的有效性。
文献[14]的融化试验采用兰州粉土制成的土柱直径10 cm、高度10 cm,初始体积含水率ω 为22.3%,初始温度为-1 ℃,试验过程始终保持土柱底部温度为-1 ℃,顶部温度为1 ℃。
采用有限元软件COMSOL 建立高度为10 cm的一维土柱模型,土体采用二次拉格朗日单元模拟,水分场、温度场的初始值和边界条件与文献[14]的试验相同。参考文献[17-18],模拟中粉土参数取值见表1。文献[14]的试验和数值模拟得到的试样含水率分布、试样温度分布如图1和图2所示。迁移,所以在冻结温度附近水分大量聚集,形成含水率峰值;土柱温度基本成线性分布,符合实际。

表1 融化试验模型参数取值
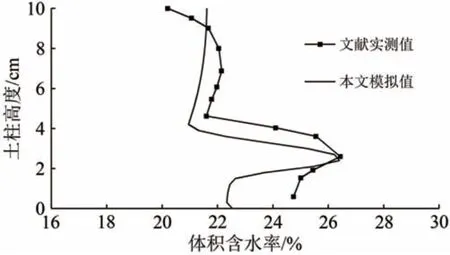
图1 融化试验中的体积含水率分布
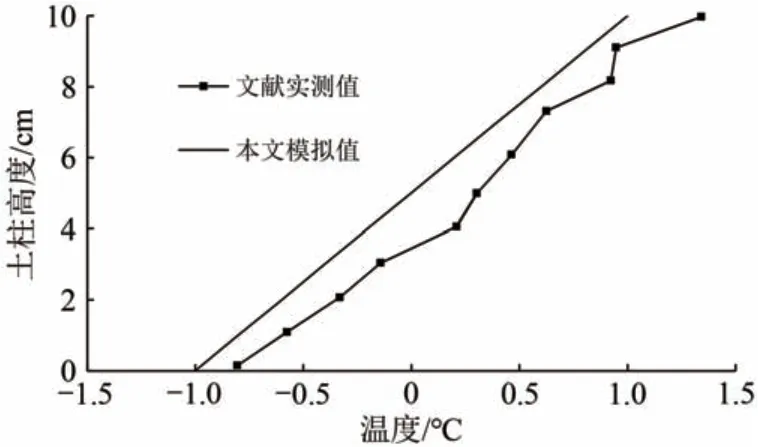
图2 融化试验中试样的温度分布
可见,采用本文冻土水热耦合计算控制方程可较准确地模拟冻土中水分迁移和温度场变化,可采用该方法对多年冻土区路基填筑问题进行模拟研究。
3 模型建立
参考青藏铁路北麓河试验段路基断面[19-20],采用有限元软件COMSOL 建立路基模型。地基宽50 m,深20 m;路基宽8 m,高4 m,坡比固定为1∶1.5。为提高计算效率,取对称模型的一半进行计算,如图3 所示。路基和地基均采用三角形单元模拟,主要计算参数见表2。
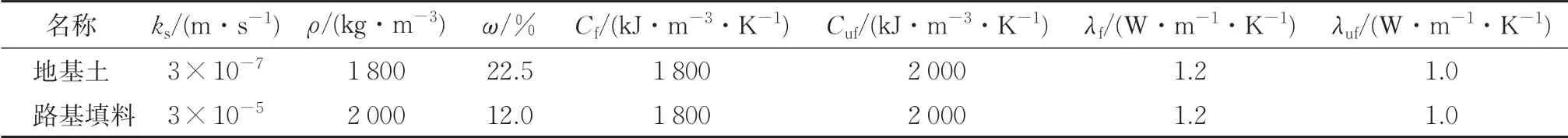
表2 路基模型主要参数
图3 模型示意图
由图1 和图2 可知:模拟结果和试验实测值基本吻合;含水率在土柱上半部分基本恒定且小于初始值,这是上部冻土融化后液态水在水力梯度和温度梯度共同作用下向下迁移导致;含水率在土柱下半部分随温度降低先增大后减小,出现含水率峰值,这是因为冻结温度附近水力梯度大、水分迁移速度快,而冰的阻滞作用使得液态水难以继续向下
参考文献[8,22-23]中青藏铁路北麓河试验段相关监测数据确定模型的温度边界。模型温度场左、右边界为绝热边界,底部采用狄利克雷边界,取-0.8 ℃,顶部温度Ttop随时间周期变化,即
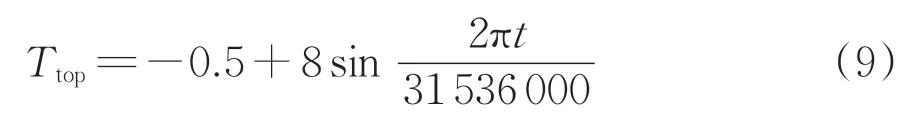
由于高原高寒地区一般在暖季施工,即每年的4 月至10 月,因此式(9)中的t=0 s 时对应时间为每年的4月15日。模型水分场左、右边界为零通量边界,底部、顶部均为狄利克雷边界,底部未冻水体积分数为0.12,顶部考虑蒸发作用较为干燥,未冻水体积分数为0.05。
地基土的水分场和温度场初始值通过计算求得。在没有路基条件下,给定地基土初始温度和未冻水体积分数分别为-0.8 ℃和0.12,然后采用前文所述边界条件进行计算,求解得到50 a后地基土的温度场和水分场初始值。
经过运输、压实等过程的填料温度往往高于地表平均温度,偏安全考虑,路基填筑完填料温度比地表温度高10 ℃。填料未冻水体积分数为0.12。本文重点关注短期内路基填筑热效应,计算时长取为90 d。
4 路基填筑短期内冻土温度场
路基的填筑会在短期内对冻土温度场产生较大影响,影响因素主要来源于初始条件、路基尺度和填料热力学性质3方面。初始条件包括路基填筑时间和填料与地表温差。对于地基而言,4 月至7 月地表温度持续升高,地基土从地表吸入热量;7 月至10 月地表温度逐渐减低,地基土向地表输出热量。因此,分别选取4 月、7 月和10 月3 个关键时间节点进行计算,研究填筑时间的影响。路基尺度包括路基高度和宽度。填料热力学性质包括体积热容和导热系数。
4.1 填筑时间的影响
图4 和图5 分别为4 月、7 月和10 月进行路基填筑后30 和60 d 的温度场,图中红色粗实线代表冻结锋面,即0 ℃刻度线位置。
由图4 和图5 可知:填筑后30 d 时,最高温度出现在路基中心位置,说明此时路基填料的热量仍在持续向大气和地基传递;填筑后60 d 时,4 月填筑路基温度场分布从地表到地基逐渐降低,与天然地基的温度分布规律一致,说明路基填料的热量已经基本耗散完毕,而7月和10月填筑路基高温区域均出现在路基中心位置且显著高于天然地基,说明填料的热量仍在持续向大气和地基传递。
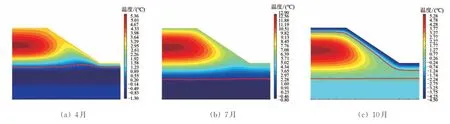
图4 填筑后30 d的温度场
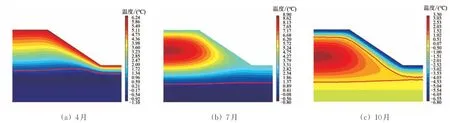
图5 填筑后60 d的温度场
冰的阻滞作用使得冻结土体渗透系数显著低于融化土体,冻土融化产生的水分以及从地表渗入地基的水分往往聚集在冻结锋面附近难以下渗,并在重力的作用下沿冻结锋面向下凹处流动、汇集。从地表渗入的水分温度较高,带有一定热量,在下凹处汇集会使得该处冻土受到热侵蚀继续融化、冻结锋面下降、下凹程度增大,而这促使周围水分继续向冻土锋面下凹处汇集,使得该处冻结锋面下凹扭曲程度持续增大。
实际工程中,路基填筑的热效应使得路基覆盖范围冻结锋面下凹扭曲,即便扭曲程度较小、与天然冻结锋面差值仅几个厘米,在水分汇入充足的情况下也可能引起持续性的下凹扭曲,产生路基热融沉降、路基开裂等病害。因此,相较于冻结锋面的绝对高程,更关心路基填筑后的冻结锋面下凹扭曲程度,即路基覆盖范围冻结锋面与天然地基冻结锋面的高程差值。
图6 为路基覆盖范围冻结锋面高程差随时间发展曲线,正值表示该处冻结锋面位置高于天然场地,负值表示低于天然场地,即该处冻结锋面发生下凹扭曲。
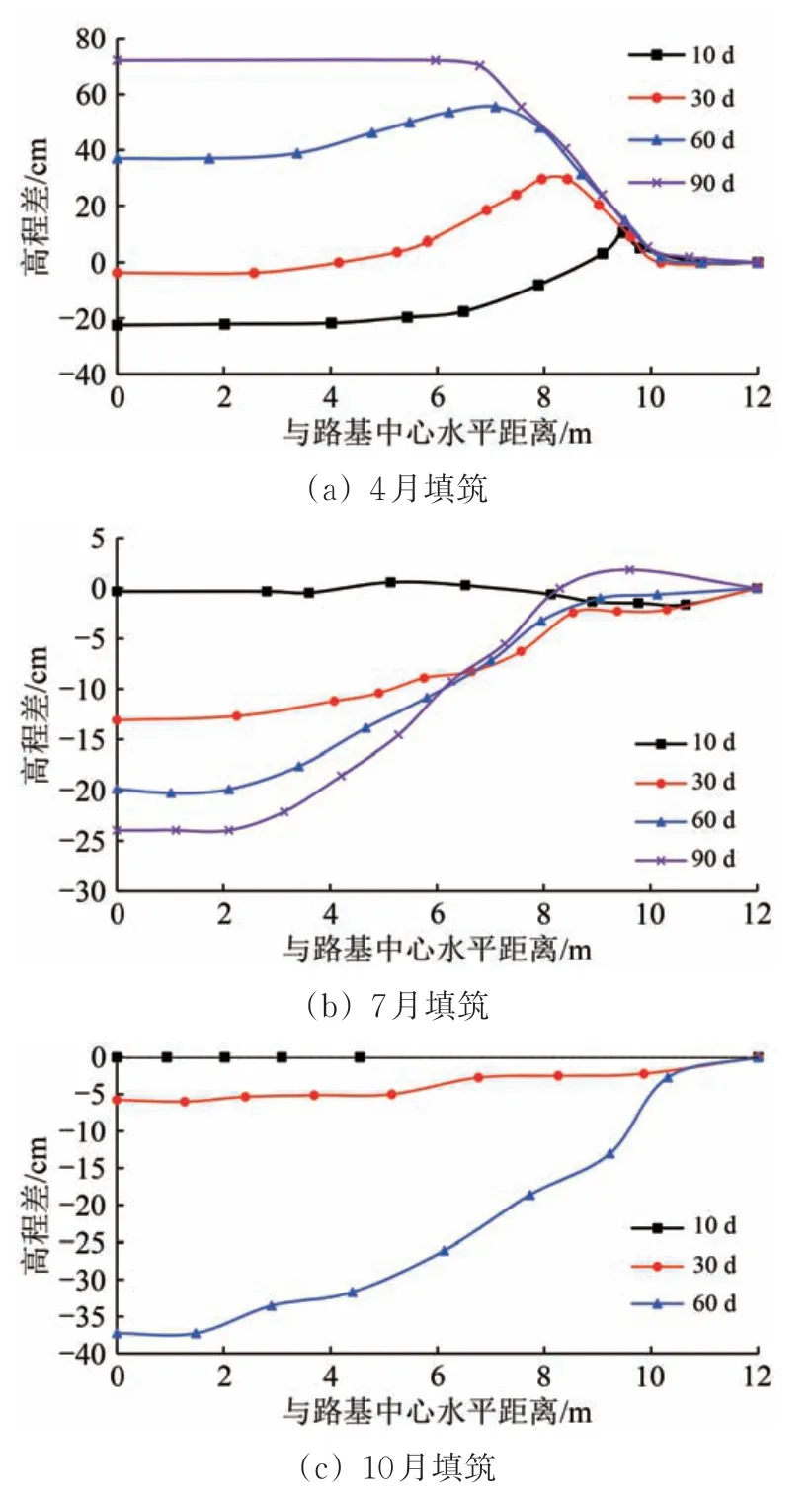
图6 路基覆盖范围冻结锋面高程差随时间发展曲线
由图6(a)可知:4 月填筑时,路基中心冻结锋面先下凹扭曲,最大下凹深度20 cm,然后随时间增大下凹程度逐渐减小,最后变成上凸扭曲;坡脚位置填筑后持续上凸。从工程角度出发,坡脚冻结锋面上凸扭曲可以阻碍路基外侧水的汇入,对工程而言是有利的。但同时坡脚上凸可能会使得路基外侧水分以及沿坡面流下的水分在坡脚外侧聚集,引发坡脚处的水热侵蚀。
由图6(b)可知:7 月填筑时,路基覆盖范围冻土场下凹扭曲程度持续增大,路基中心冻结锋面高程差从0 增至25 cm;路基坡脚仅在填筑后90 d才观察到轻微上凸扭曲。夏季降雨较多,地表水丰富且温度高、热量大,此时冻土场发生下凹扭曲最容易引发水热侵蚀,于工程而言是最危险的。
由图6(c)可知:10 月填筑时,路基覆盖范围冻土场下凹扭曲程度持续增大,路基中心冻结锋面高程差从0 增至38 cm;坡脚并未观察到上凸扭曲。虽然10 月填筑后相同时间内的冻土场下凹扭曲程度最大,但考虑到填筑后地表温度很快降到0 ℃以下,地表水较少且温度低,不易引起水热侵蚀。
图7 为4 月、7 月和10 月填筑后路基中心与天然场地冻结锋面高程差随时间发展曲线。由图7可知:4 月填筑时路基中心冻结锋面高程差发展规律与7 月、10 月填筑不同,4 月填筑后路基中心冻结锋面先下降后上升,而7月、10月填筑后路基中心冻结锋面持续下降,即路基覆盖范围下凹扭曲程度持续增大;7 月填筑后冻结锋面高程差绝对值与时间近似成对数关系,而10 月填筑后冻结锋面高程差随时间增加而急剧增大,直至路基覆盖范围形成封闭的融化核。后续研究将以7 月填筑为基础展开。
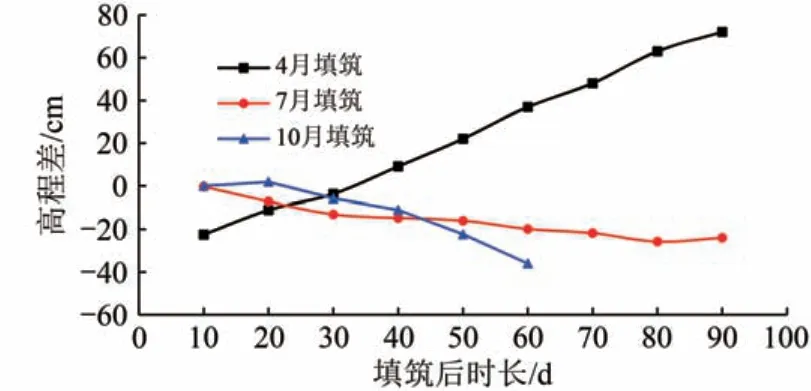
图7 路基中心冻结锋面高程差随时间发展曲线
4.2 路基填料与地表温差的影响
图8 和图9 分别为填料温度与地表温度差不同时,填筑后90 d路基覆盖范围冻结锋面下凹扭曲曲线和路基中心与天然场地冻结锋面高程差。
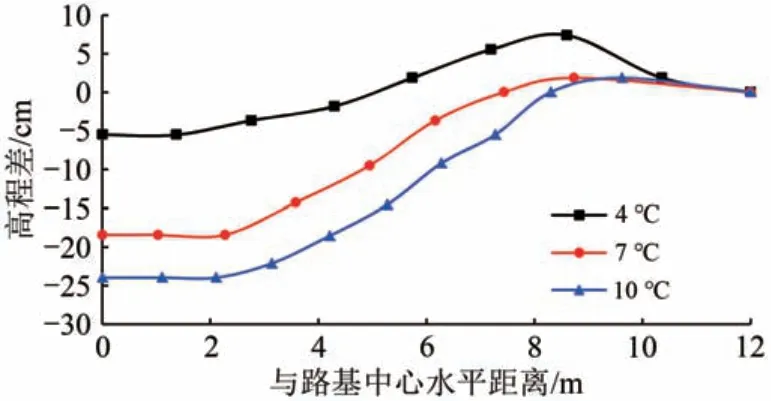
图8 路基覆盖范围冻结锋面高程差曲线
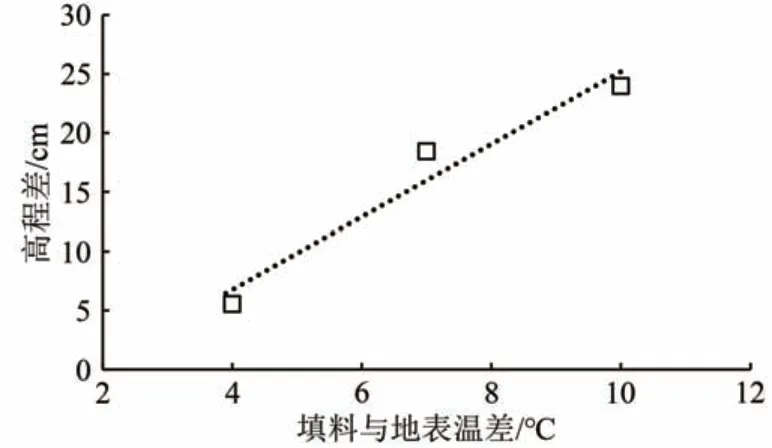
图9 路基中心冻结锋面高程差随路基填料与地表温度变化曲线
由图8 可知:路基覆盖范围冻结锋面下凹扭曲程度随填料与地表温差增大而增大;当温差为4 ℃时,在坡脚位置还可观察到明显的冻结锋面上凸扭曲,可在一定程度上阻碍周围水分向路基中心底部汇聚。
任一超过材料或结构疲劳极限的应力的循环作用均会对材料或结构造成不同程度的损伤,而造成的损伤是累积的,当损伤累积达到材料或结构疲劳失效的临界值时材料或结构就会出现疲劳损坏。
由图9 可见:路基中心与天然场地冻结锋面高程差随温差增大而增大。
4.3 路基尺度的影响
图10 和图11 分别为路基高度不同时,填筑后90 d路基覆盖范围冻结锋面下凹扭曲曲线和路基中心与天然场地冻结锋面高程差。
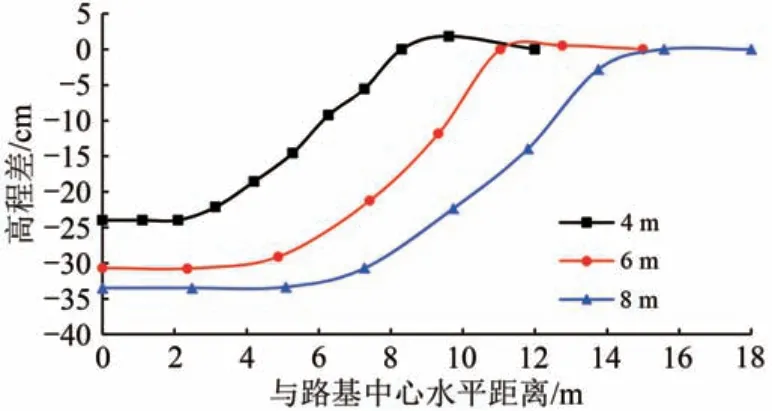
图10 路基覆盖范围冻结锋面高程差曲线
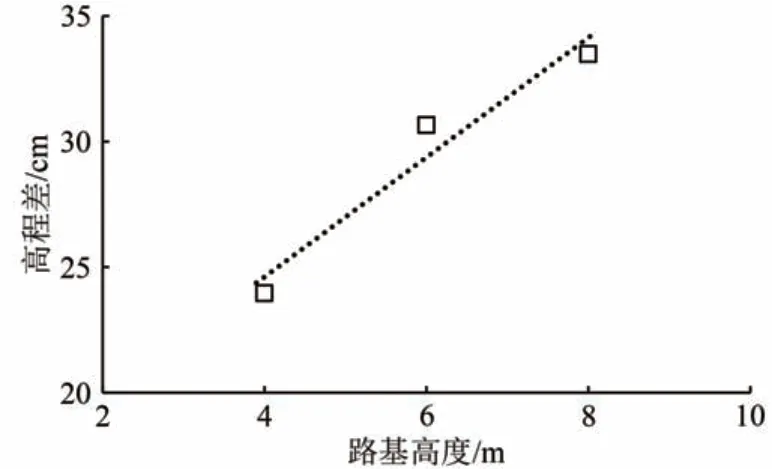
图11 路基中心冻结锋面高程差随路基高度变化曲线
由图10 可知:路基覆盖范围冻结锋面下凹扭曲程度随路基高度增大而增大。
由图11 可见:路基中心与天然场地冻结锋面高程差随路基高度增大而增大。
图12 和图13 为路基宽度不同时,填筑后90 d路基覆盖范围冻结锋面下凹扭曲曲线和路基中心与天然场地冻结锋面高程差。
由图12 可知:路基覆盖范围冻结锋面下凹扭曲程度随路基宽度增大而增大。
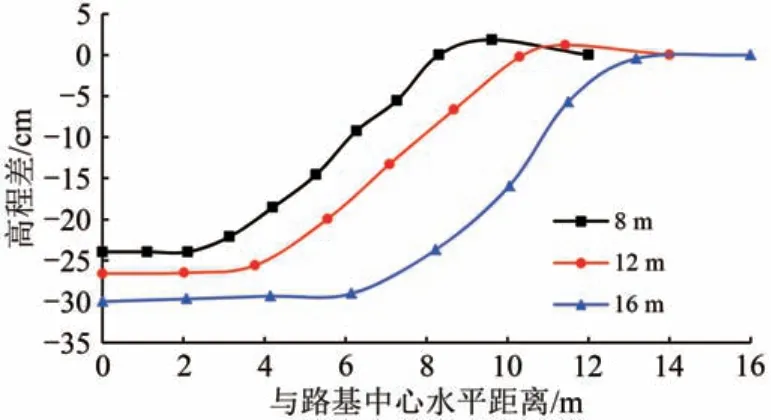
图12 路基覆盖范围冻结锋面高程差曲线
由图13 可见:路基中心与天然场地冻结锋面高程差随路基宽度增大而增大。
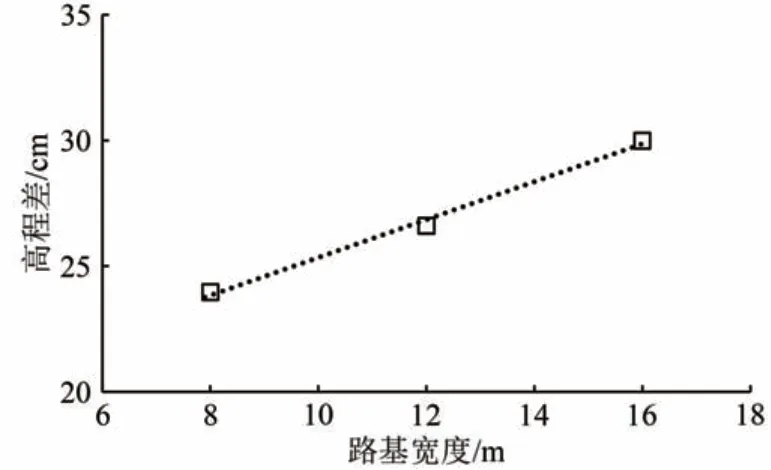
图13 路基中心冻结锋面高程差随路基宽度变化曲线
4.4 填料热力学性质的影响
图14 和图15 分别为填料导热系数(冻结状态)不同时,填筑后90 d路基覆盖范围冻结锋面下凹扭曲曲线和路基中心与天然场地冻结锋面高程差。
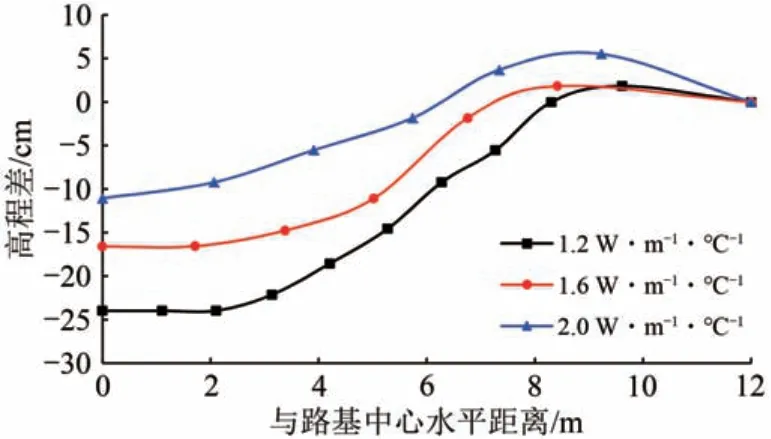
图14 路基覆盖范围冻结锋面高程差曲线
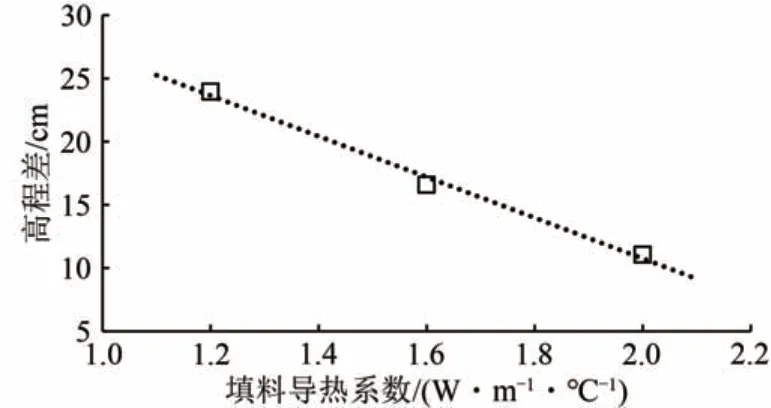
图15 路基中心冻结锋面高程差随填料导热系数变化曲线
由图14 可知:路基覆盖范围冻结锋面下凹扭曲程度随填料导热系数增大而减小;当填料导热系数为2.0 W·m-1·℃-1时,在坡脚位置还可观察到明显的冻结锋面上凸扭曲,可在一定程度上阻碍周围水分向路基中心底部汇聚。
由图15 可见:路基中心与天然场地冻结锋面高程差随填料导热系数增大而减小。
图16和图17分别为填料体积热容(冻结状态)不同时,填筑后90 d路基覆盖范围冻结锋面下凹扭曲曲线和路基中心与天然场地冻结锋面高程差。
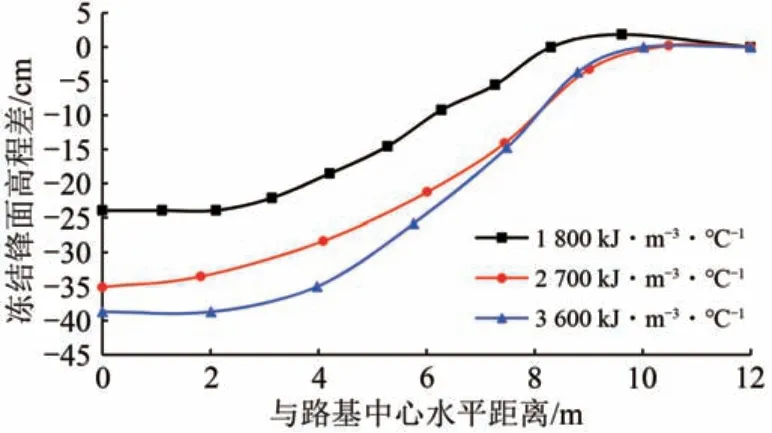
图16 路基覆盖范围冻结锋面高程差曲线
由图16 可知:路基覆盖范围冻结锋面下凹扭曲程度随填料体积热容增大而增大。
由图17 可见:路基中心与天然场地冻结锋面高程差随填料体积热容增大而增大。
5 路基填筑短期内冻结锋面计算方法
冻结锋面下凹扭曲曲线可用倒梯形近似描述,如图18所示。
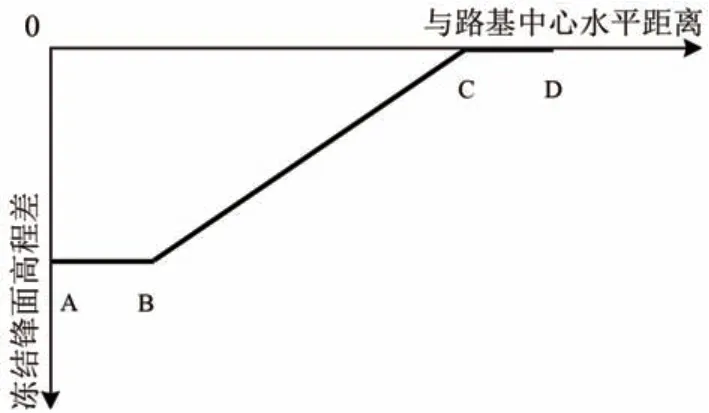
图18 冻结锋面下凹扭曲示意图
该曲线可分为AB,BC和CD 3段:AB段为路基中心部分,该区域与天然场地冻结锋面高程差最大,且差值基本恒定,不随水平位置的变化而改变;BC段为路基肩部到路基坡脚的部分,该区域与天然场地冻结锋面高程差迅速降低,近似线性变化;CD段对应路基坡脚及相邻区域,该区域与天然场地冻结锋面高程差基本为0。因此冻结锋面高程差Δh 可表示为
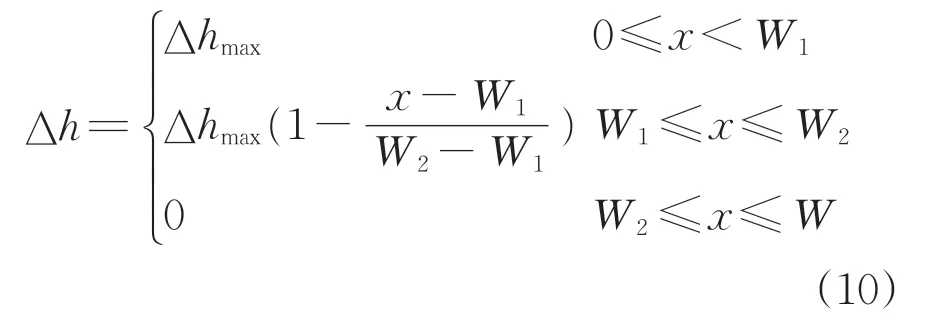
式中:Δhmax为路基中心的冻结锋面高程差,即图18 中的OA;W1为路基中心的冻结锋面高程差稳定段宽度,即图18 中的AB;W2为冻结锋面变化宽度,即图18 中的OC;W 为路基中心与坡脚距离,即图18中的OD。
以上参数的具体计算如下。
(1)Δhmax与时间近似成对数关系,随填料与地表温差、路基高度、路基宽度和填料体积热容的增大而增大,随填料导热系数增大而减小。根据图7、图8、图9、图10、图11、图13 和图15 中的计算结果,拟合得到Δhmax为

式中:tf为填筑后时长,d;ΔT 为填筑时填料与地表温差,℃;h 为路基高度,m;W路基为路基宽度,m;Cf为填料冻结时的体积热容,J·m-3·K-1;λf为填料冻结时的导热系数,W·m-1·K-1。
(2)W 由路基高度和宽度2个参数确定,计算公式如下。

(3)W1由路基高度和宽度2 个参数确定,计算公式如下。
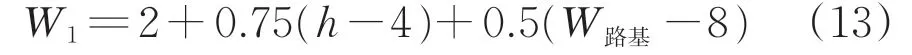
(4)W2随路基高度和宽度的增大而增大,随填料导热系数的增大而减小,根据图14 中的计算结果,拟合得到计算式如下,即
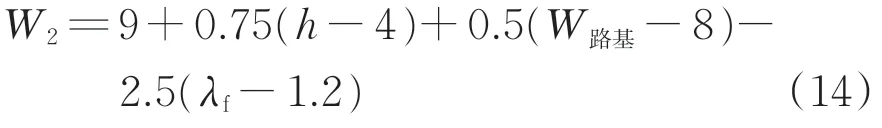
6 结 论
(1)路基填筑后短期内路基中心下方冻结锋面发生下凹扭曲,在水分汇入充足情况下将引发水热侵蚀,导致冻结锋面持续性的下凹扭曲,进而可能产生路基热融沉降、路基开裂等病害,工程中需做好防水工作。
(2)与4 月填筑和10 月填筑相比,7 月填筑时最大程度阻碍了土体热量向大气中输出,路基覆盖范围冻结锋面下凹扭曲程度最大、冻土温度场恢复最慢,属于最不利工况。
(3)路基覆盖范围冻结锋面下凹扭曲程度随填料与地表温差、路基高度、路基宽度、填料体积热容的增大而增大,随填料导热系数增大而减小,因此实际工程中应尽量选用体积热容小、初始温度低,且导热系数大的填料。
(4)提出路基覆盖范围冻结锋面下凹扭曲计算方法,并给出关键参数确定方法。采用该方法可得到填筑完成后不同时刻、不同工况下的冻结锋面下凹扭曲曲线。
