高新技术企业知识员工离散动态系统建模及其弹性控制

戴 丹,蔡智辉,张宝琳

(1.中国计量大学 理学院，浙江 杭州 310018；2.青岛科技大学 自动化与电子工程学院，山东 青岛 266061)

21世纪的经济形态是知识经济形态，而高新技术企业是知识经济发展的微观基础和重要载体。随着科学技术的进步，自然资源对社会发展的支撑力逐步下降，而人才资源的作用正在不断上升。人才资源的占有决定了高新技术企业的发展，是否拥有一支高素质高水平的人才队伍是提升高新技术企业核心竞争力的关键。但是，近年来，大量研究表明，世界各地大部分企业都存在人才短缺和人才流失的问题[1-6]。吸引和稳定优秀的人才已经成为高新技术企业目前急需解决的问题。

企业人力资源管理问题是业界的热点研究领域之一，特别地，企业人力资源需求预测方法和规划问题的研究一直是学者们普遍关注的课题。例如，文献[7]通过对人力资源需求进行分析，研究了改进的马尔科夫模型在人力资源管理问题中的应用,文献[8]研究了企业人力资源需求预测的BP神经网络方法,文献[9]通过分析企业对人力资源的需求，给出了有利于企业发展的人力资源规划方案。注意到，这些方法大部分是基于静态的、确定性的角度进行研究。事实上，企业人力资源发展往往是动态的、不确定的。因此，从动态系统的观点，采用现代控制理论和方法研究企业人力资源管理问题逐渐成为一个热点课题。近年来，很多学者开始关注人力资源的动力学行为，并从系统控制的角度研究人力资源的演进规律以及招聘策略。特别地，在知识经济时代，知识型人才在企业中的作用越来越重要，对知识型人才队伍的建设和管理尤为关键。例如，文献[10-11]研究了如何在多个不确定性因素的干扰下保持知识型员工队伍系统动态稳定的问题，建立了知识型员工系统的动力学模型，设计了人力资源系统的鲁棒最优保性能控制律，给出了不同情形下知识型员工的管理策略。文献[12]讨论了企业人力资源规划问题，采用鲁棒优化的方法对人员流动模型进行改进，解决了由于不确定因素的干扰导致的由人力资源规划模型得出的结果与实际存在偏差的问题。文献[13]分析了现代控制理论在知识型员工队伍系统稳定性分析中的应用，讨论了不同情形下知识员工系统的鲁棒稳定性。上述文献虽然对知识型员工系统建立了动态模型并研究了使系统达到渐近稳定的充分条件，但大多数是基于连续模型进行研究。实际中，企业的招聘或辞退都是在一个固定的阶段或周期内进行的，企业的人力资源管理系统呈现出显著的离散系统特性。因此，建立知识型企业人力资源系统的离散动力学模型，进而研究企业人力资源的招聘策略和动态管理具有重要现实意义。

在设计动力系统的反馈控制器时，控制器参数的时变摄动可能导致闭环系统的性能下降，甚至稳定性也会遭到破坏，为此提出了弹性控制的概念。弹性控制是指控制行为能够适应组织内部条件与外部环境的变化，具有一定的灵活性和抗干扰性。弹性控制通常与控制的标准有关，有时也与控制系统的设计有关[14]。近年来，对不确定系统的弹性控制器的研究受到了许多学者的广泛关注[15-16]。注意到，人力资源系统在招聘或辞退的过程中，由人力资源规划模型得出的理论招聘结果与实际招聘行为之间可能存在偏差。换言之，企业每个招聘周期实际的招聘(或辞退)数据并不是精确匹配其理论结果，实际招聘(或辞退)数据往往与在理论结果有一定的摄动。该招聘(或辞退)数的时变摄动往往会给人力资源系统的性能带来影响。幸运的是，弹性控制的思想为解决这一问题提供了可行性。目前，基于弹性控制的思想研究人力资源系统招聘问题的文献目前还不多见，本文尝试结合弹性控制方法，研究高新企业人力资源管理系统的招聘策略。

本文从系统控制的角度出发，结合高新技术企业知识人才的实际情况，研究了高新技术企业知识型人才队伍动态系统的建模和弹性招聘策略问题。文章通过分析影响高新技术企业知识型人才队伍系统稳定性的因素(招聘或离职行为、转岗行为等)，建立了企业知识型人才队伍系统的非线性时变离散系统模型。基于此模型，提出了人才队伍系统的弹性招聘策略，并分析了闭环系统渐近稳定的充分条件。所设计的招聘策略能够保证实际人才队伍系统各状态跟踪期望状态，仿真结果验证了本文提出的招聘策略的有效性。

1 模型描述

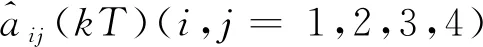
令

(1)

其中，aij和δij(kT)分别表示第j类员工转化成第i类员工转岗率的标称值和时变摄动值，|δij(kT)|<1,Δii=a1i+a2i+a3i+a4i,i,j=1,2,3,4。

在下面的讨论中，以第i类人员为例，理想情况下，假设模型不考虑招聘或辞退行为的情形,此时该类人员的动态方程可表示为

(2)

在本文中，为使知识员工管理系统达到动态稳定，需考虑招聘或辞退行为，并设计合适的招聘策略来调节员工系统的稳定性。从而，考虑员工招聘和辞退行为，该类人员的动态方程可进一步表示为

(3)

令

(4)

由式(2)、(3)和(4)，可得系统的增量方程

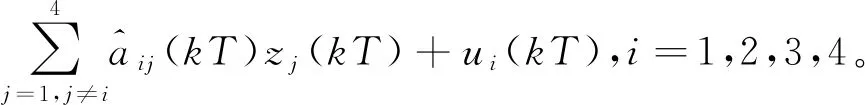
(5)

为表示简单起见，省略各式中的T，并令

(6)

其中，时变不确定项gi(z(k))可表示为：

(7)

于是，方程(5)可以改写为

z(k+1)=Az(k)+u(k)+g(z(k))，z(0)=z0。

(8)

其中，z0为初始状态，

(9)

设时变不确定项g(z(k))满足下面约束条件：

(10)

其中，μ>0为给定的常数。

假设企业员工系统中各类人才的期望数量由下面动态方程描述：

r(k+1)=Gr(k)，r(0)=r0。

(11)

其中，G为给定的4×4已知矩阵，r0为期望系统的初始状态。

本文的目的在于设计企业招聘策略，使得企业各类人才数量能够按照期望模型(11)变化。为此，引入误差向量：

e(k)=z(k)-r(k)，e(0)=e0。

(12)

于是，由式(8)、(11)和(12),可得

e(k+1)=Az(k)-Gr(k)+u(k)+g(z(k))，
e(0)=e0。

(13)

令

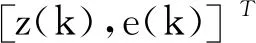
由式(8),(11)至(13)可得增广系统为

h(k+1)=Hh(k)+Mu(k)+Mg(z(k))，
h(0)=h0。

(14)

其中，

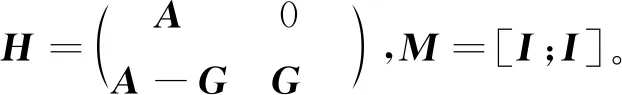
(15)

在招聘过程中，企业政策、招聘成本等不确定性因素对招聘会产生一定的影响，为此，基于弹性控制策略设计知识型员工的企业招聘策略，令系统的弹性控制律(招聘或辞退律)为

u(k)=(K+ΔK(k))h(k)。

(16)

其中，K为待设计的4×8增益矩阵，ΔK(k)为如下形式的时变摄动矩阵：

ΔK(k)=EΓ(k)F。

(17)

式(17)中E和F均为已知的适当维数矩阵，Γ(k)是时变扰动矩阵，且Γ(k)满足ΓT(k)Γ(k)≤I，I为适当维数的单位矩阵。

将(16),(17)代入(14)式，可得闭环系统为

h(k+1)=(H+MK+MEΓ(k)F)h(k)+
Mf(h(k))。

(18)

其中，f(h(k))：=g(z(k))。

为了得到本文的主要结果，先引入以下引理。

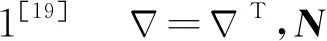
(19)

(20)

其中ε>0。

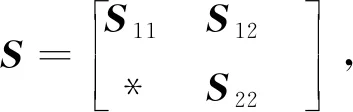
1)S<0；

2 员工队伍系统的稳定性分析

选取如下Lyapunov函数：

V(k)=hT(k)Ph(k)。

(21)

其中，P是8×8对称正定矩阵。

式(21)沿着闭环系统(18)关于k的向前差分为

ΔV(h(k))=hT(k)(H+MK+MEΓ(k)F)TP

(H+MK+MEΓ(k)F)h(k)+2hT(k)

(H+MK+MEΓ(k)F)TPf(h(k))-

hT(k)Ph(k)+fT(h(k))Pf(h(k))。

(22)

由(10)式可得

亦即

μ2hT(k)h(k)-fT(h(k))f(h(k))≥0。

(23)

于是，由式(22)和(23)可得

ΔV(h(k))≤ηT(k)Σ(k)η(k)。

(24)

其中，

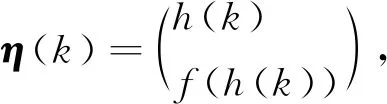
(25)

式(25)中，φ(k)=H+MK+MEΓ(k)F。

由离散系统稳定性理论，系统(18)渐近稳定,只需Σ(k)<0。事实上，Σ(k)<0当且仅当

Γ+Ω(k)<0。

(26)

其中

(27)

注意到式(26)等价于

(28)

由Schur补引理，式(28)等价于

(29)

亦即

(30)

事实上，式(30)等价于

(31)

由引理1知上述不等式等价于

(32)

再次运用Schur补引理，上式等价于

(33)

为了得到知识员工系统的招聘增益矩阵K，式(33)左边矩阵分别左乘和右乘矩阵diag{P-1,I,I,I,εI,I}及其转置矩阵，并令

(34)

我们有

(35)

基于上述分析，我们有下面结论。

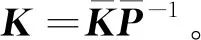
特别地，如果不考虑招聘增益矩阵摄动的情形，即ΔK(k)=0，则对应的闭环系统为

h(k+1)=(H+MK)h(k)+Mf(h(k))。

(36)

在这种情况下，基于定理1，容易得到系统(18)渐近稳定的一个充分条件。

推论1对于给定标量μ>0，适当维数矩阵M如果存在8×8对称正定矩阵P和4×8矩阵K，使得下面矩阵不等式成立：

(37)

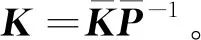
注1通过u(k)的求解，可以得到知识员工保持动态稳定的招聘、辞退人数；同时，企业管理人员可以将u(k)与企业实际数据比较，进一步调整和优化人才队伍。若ui≥0，表示企业第i类人才短缺，应该及时进行招聘。若ui<0，表示企业人员冗余度高，应辞退第i类人才。

3 数值仿真

为了验证本文提出的高新技术企业知识员工弹性招聘策略的有效性，以某公司专业技术人员、管理人员、销售人员和工勤人员近二十个招聘周期的相关数据为例进行说明。

3.1 系统参数

设四类知识人员转岗率以及离职率标称值对应的参数为：

a11=0.01,a21=0.03,a31=0.01,a41=0,
a12=0.01,a22=0.01,a32=0.02,a42=0.01,
a13=0.02,a23=0.04,a33=0.03,a43=0.01,
a14=0.01,a24=0.02,a34=0.02,a44=0.03。

于是，由(9)式计算可得系统矩阵为

设期望系统(11)的系统矩阵G=diag{0.9,0,35,-0.75,-0.45}，设员工系统(8)和期望系统(11)的初值分别为z(0)=[-10,20,15,-15]T。令μ=0.6，时变不确定项g(z(k))用如下正弦函数向量近似：g(z(k))=μ[sin(z1(k))

sin(z2(k)) sin(z3(k)) sin(z4(k))]T。

3.2 情形1 ΔK(k)=0

通过求解线性矩阵不等式(37)，可得招聘增益矩阵K为

于是，对应的员工系统招聘方案即可确定。在此招聘方案下，在给定的招聘周期内，四类员工在不同招聘周期对应的应该招聘(或辞退)数曲线由图1给出；对应地，四类人员数的增量曲线和跟踪误差曲线分别由图2和图3给出。

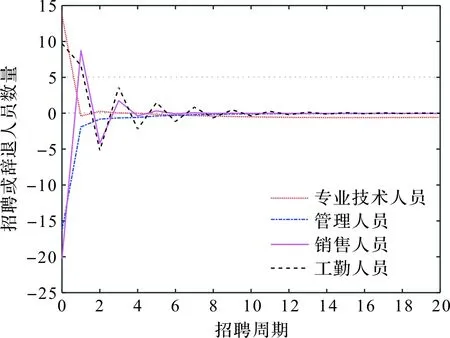
图1 ΔK(k)=0时员工招聘或辞退数曲线Figure 1 Curve of recruitment or dismissal numbers of staff as ΔK(k)=0

图2 ΔK(k)=0时员工人数增量曲线Figure 2 Incremental curve of staff numbers as ΔK(k)=0

图3 ΔK(k)=0时员工数跟踪误差曲线Figure 3 Tracking error curve of staff numbers as ΔK(k)=0

图1给出了在不同的招聘周期，知识员工系统4类人员应该招聘或辞退的员工数。由图2和图3可以看到，在对应的招聘策略下，知识员工系统(8)能够保持鲁棒渐近稳定，且4类员工可以实现对期望值的渐近跟踪。

情形2ΔK(k)≠0

下面，我们讨论控制增益存在摄动的情形。为此，式(17)中，时变不确定项Γ(k)为取值在-0.98到0.98之间的随机函数，令

其中，F1=diag{0.2,-0.4,-0.3,0.2},F2=diag{0.1,0.1,0.1,0.1}。其它参数的取值同情形1。

通过求解线性矩阵不等式(35),可得招聘增益矩阵K的值为

于是，员工系统的弹性招聘策略可以确定。在此招聘方案下，四类员工在不同招聘周期对应的应该招聘(或辞退)数曲线由图4给出，四类人员数的增量曲线和跟踪误差曲线分别由图5和图6给出。可以看到，即使招聘增益矩阵存在摄动，亦即招聘过程中可能存在不确定性因素，知识员工系统(8)在所设计的弹性招聘策略下仍然能够保持鲁棒渐近稳定，且企业中4类员工可以实现对期望系统值的渐近跟踪。

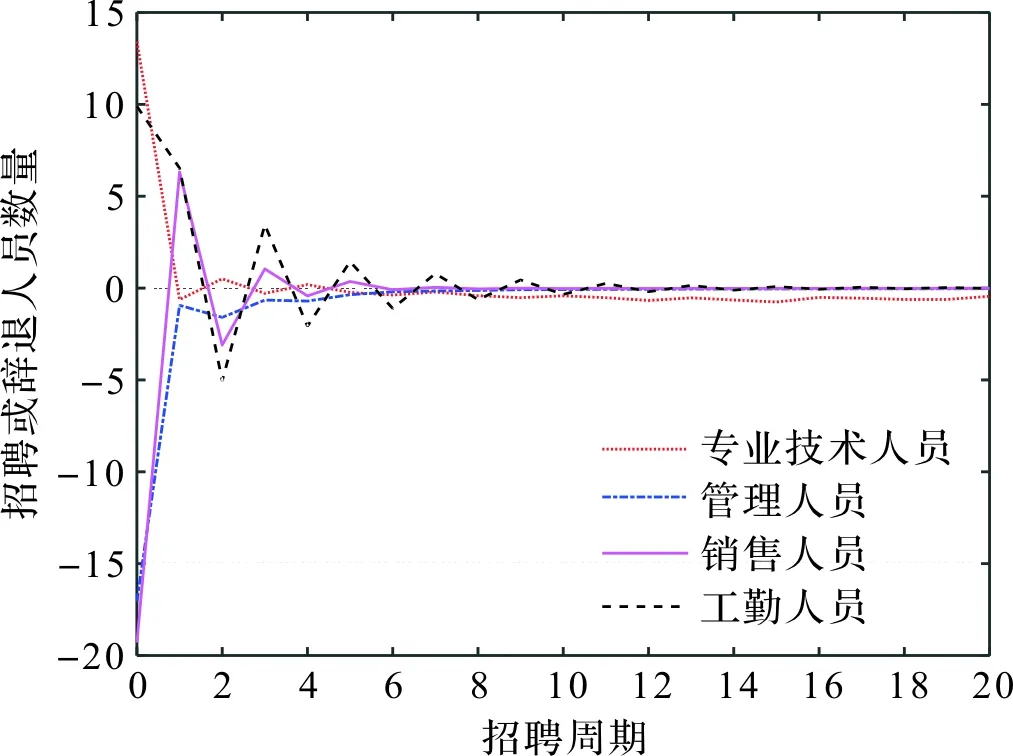
图4 ΔK(k)≠0时员工招聘或辞退数曲线Figure 4 Curve of recruitment or dismissal numbers of staff as ΔK(k)≠0

图5 ΔK(k)≠0时员工人数增量曲线Figure 5 Incremental curve of staff numbers as ΔK(k)≠0

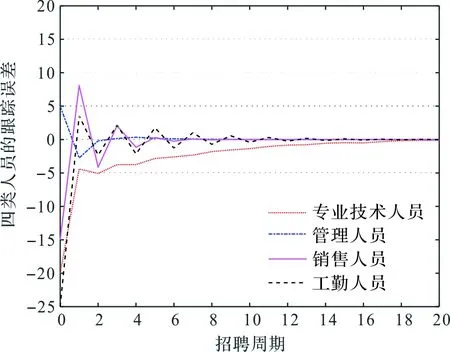
图6 ΔK(k)≠0时员工数跟踪误差曲线Figure 6 Tracking error curve of staff numbers as ΔK(k)≠0

4 结 语

本文研究了高新技术企业知识员工的离散系统动力学建模及其弹性控制器的设计问题，将动态知识员工管理系统表示为一类非线性时变离散系统，通过考虑招聘增益矩阵存在摄动的情形，基于李雅普诺夫稳定性理论，提出了高新技术企业知识员工人才队伍系统弹性招聘策略的设计方法。仿真结果表明本文设计的弹性控制策略能使高新技术企业知识员工系统渐近稳定，有利于高新企业人才队伍建设和稳定。