固定式海洋平台系统的网络化模糊减振控制方法

冯华女，张宝琳，郭奕瑄，袁 梦，马阳顺

(1.中国计量大学 理学院，浙江 杭州 310018；2.中国计量大学 经济与管理学院，浙江 杭州 310018)

海洋平台作为海洋油气资源开发的基础设施之一，长期处于恶劣的海洋环境中，平台结构不可避免地受到了波浪、风、冰和地震等外部载荷的影响[1-4]。通常，这些外部载荷导致了平台的过度振动,研究表明，如果能够有效降低海洋平台的振动幅值，则可以大幅延长海洋平台的使用寿命，大量减少平台的检查和维护成本，有效保障平台上工作人员的安全[5]。因此，研究海洋平台的减振控制问题十分重要。

海洋平台的减振控制方法包括被动控制、半主动控制、主动控制和混合控制等。与被动控制方法相比，主动控制方法通常具有更好的控制效果，更广的适用范围，更灵活的控制目标。因此，结构主动控制方法的理论和应用研究一直是重要的热点课题之一。近年来，海洋平台结构振动主动控制方法研究越来越引起人们的关注[6-7]。例如，针对一类安装主动质量阻尼器机构的钢结构海洋平台简化模型，文献[8]通过引入波浪力外系统模型，进而提出了海洋平台系统的前馈反馈最优控制，该方法能有效减小波浪力引起的海洋平台振动。进而,基于该模型，文献[9]和[10]进一步分别研究了基于滞后反馈的控制方法和采样控制方法。针对一类具有调谐质量阻尼器的海洋平台模型，通过考虑结构参数不确定性因素建立了海洋平台的不确定性非线性模型，提出了基于时滞反馈的滑模变结构控制方法，并分析了引入时滞对海洋平台性能的正面作用[11]。随着数字化技术的发展，网络化控制系统成为控制理论与控制工程领域的重要研究课题[12-13]。特别地，由于海洋平台长期处在复杂的海洋环境中，传统的点对点控制使得海洋平台振动系统的控制和维护成本增大。这种情况下，基于网络化的海洋平台振动控制问题研究非常必要，目前已有很多学者研究此类问题。例如，文献[14]和[15]研究了在网络环境下海洋平台的网络化控制系统建模及其综合问题；文献[16]基于模型变换给出了在多外力作用下的海洋平台网络控制器设计方法，文献[17]研究了考虑网络诱导时滞、网络丢包等因素的海洋平台网络化预测控制方法。

注意到海洋平台系统体积庞大，结构复杂，要建立精确的动力学模型非常困难。从现有文献也可以看到，目前有关海洋平台振动系统的研究绝大多数是基于仅考虑海洋平台一阶或二阶振动模态的简化模型。事实上，海洋平台的简化模型本质上仍然呈现非线性特性。作为解决非线性问题的有效工具之一，模糊控制系统的建模、分析和综合一直是重要的研究课题[18,19]。考虑到海洋平台上长期进行海洋油气资源的勘探、提取、储存、装载或卸载等工作，导致平台质量具有时变特性。针对具有主动质量阻尼器的海洋平台模型，文献[20]通过模糊化结构质量参数，给出了海洋平台系统的Takagi-Sugeno(T-S)模糊动力学模型，进一步研究了基于事件触发的网络化海洋平台控制器设计方法；文献[21]则讨论了海洋平台的输出反馈模糊控制方法，并基于数值仿真验证了方法的有效性。我们知道，海洋平台动力学模型中，作为重要的结构参数之一，海洋平台的固有频率通常被近似化为一个常数进行分析。事实上，海洋平台的固有频率本质上具有时变特性。为此，直接基于结构系统的固有频率进行模糊建模，进而研究海洋平台系统的主动控制问题，就具有重要意义。

本文针对具有调谐质量阻尼装置的海洋平台简化模型[1]，通过模糊化海洋平台系统的时变固有频率，研究海洋平台系统的T-S模糊动力学建模问题；进而研究该系统在网络环境下的主动减振控制，给出海洋平台系统网络化模糊控制设计方法，采用Lyapunov-Krasovskii泛函分析方法和积分不等式方法，得到了网络化模糊海洋平台闭环系统渐近稳定的充分条件；最后，通过仿真实验，验证了本文方法的有效性和优越性。

1 问题描述

考虑安装有调谐质量阻尼机制的海洋平台简化模型(图1),其动力学方程可表示为[1]：

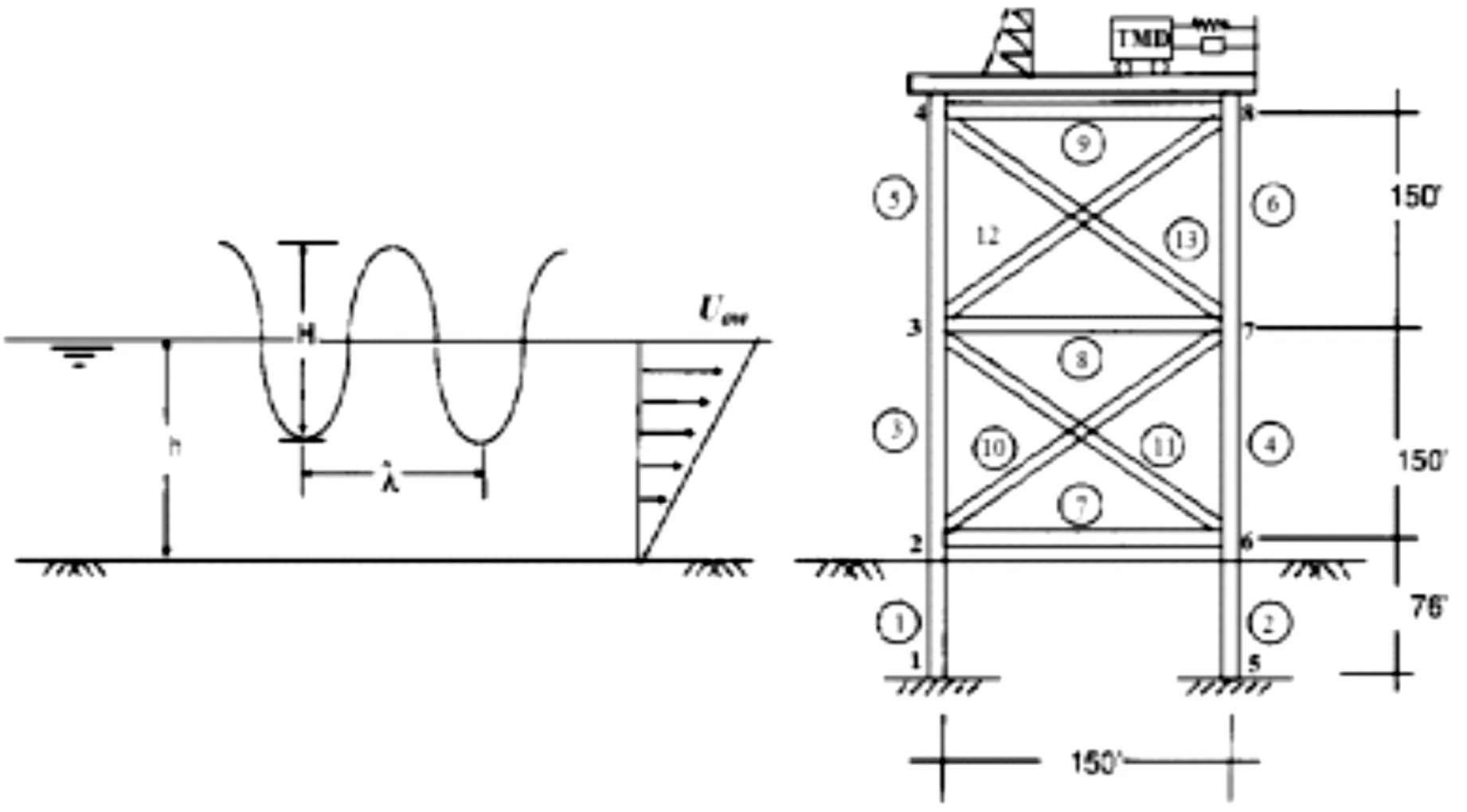
图1 海洋平台简化模型Figure 1 An idealized offshore platform

(1)

其中：z1(t)、ω1、ξ1和φ1分别代表海洋平台的第一振动模态的广义坐标、固有频率、阻尼比和形参数；z2(t)、ω2、ξ2和φ2分别代表平台的第二振动模态的广义坐标、固有频率、阻尼比和形参数；zT(t)、ωT、ξT、CT、mT和KT分别代表调谐质量阻尼器的水平位移、固有频率、阻尼比、阻尼、质量和刚度。fi(x,t)(i=1,2,3,4)是作用在平台上的非线性自激波浪力，u(t)是所需的主动控制力。

令

(2)

其中,

于是，海洋平台系统的状态空间模型可以表示为

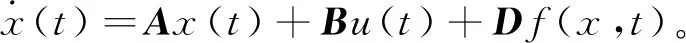
(3)

其中,

非线性自激波浪力f(x,t)一致有界且满足如下约束[1]：

(4)

其中μ是一个正实数。

注意到，系统方程(1)中，视海洋平台的固有频率为常数。事实上，平台固有频率具有时变特性，为了得到更一般化的海洋平台模型，下面我们基于固有频率的时变特性，给出海洋平台的模糊动力学模型。

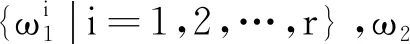
模糊规则i:如果模糊变量ω为情形i，则系统的模糊模型为

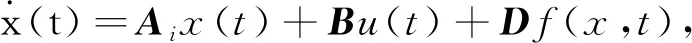
(5)

通过中心平均去模糊化方法[22]，可以得到海洋平台系统的全局动态模糊模型为

(6)

假定海洋平台处于网络环境下，图2描述了处于网络化控制的海洋平台的框架，其中采样器以采样周期h周期性的采样状态信号x(t)，采样

图2 网络环境下的T-S模糊系统框图Figure 2 A diagram of T-S fuzzy system in network environment

数据x(kh)被封装成数据包通过通信网络进行传输。假设通信信号都是以单包方式传输，且无丢包和乱序现象；同时，系统所有的状态向量都是可测的。

下面给出基于网络化的模糊控制规则。

控制规则j：如果模糊变量ω为情形i，则

u(t)=Kjx(kh)，k∈。

(7)

其中Kj(j=1,2,…,r)是相应控制规则下的增益矩阵，通过中心平均去模糊化方法得全局模糊控制律为

(8)

注意到

x(kh)=x(t-(t-kh))。

因此时滞τ(t)可表示为

τ(t)=t-kh,
t∈[kh+τm,(k+1)h+τM),k∈。

其中τm和τM分别是网络诱导时滞τ(t)的下界和上界，且τM≥τm≥0。

注意到，τ(t)满足下面条件：

(9)

其中τ1=τm,τ2=τM+h。

因此基于网络化的模糊控制器为

(10)

将模糊控制器(10)代入到海洋平台模糊系统(6)，得

(11)

为简化起见，令

υ(t)=col{x(t),x(t-τm),x(t-τ(t)),
x(t-τM),f(x,t)}。

则闭环系统(11)可表示为

(12)

其中Θij=[Ai,0,BKj,0,D]。

为了得到本文的主要结果，首先给出如下引理。

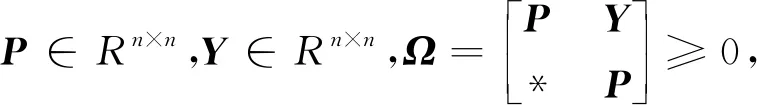
其中

引理2[19]对于任意的实矩阵Xi，Yi，i={1,2,…,δ}和适当维度的正定矩阵P>0，则下列不等式成立：

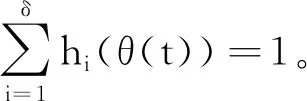
2 网络化模糊控制器设计

下面给出海洋平台网络化模糊控制器存在的充分条件。

定理1：给定标量0≤τm≤τM，h>0和0<μ<1，如果存在6×6矩阵P>0，Q0>0，Q1>0，R0>0，R1>0，U1，1×6矩阵Kj(j=1,2,…,r)以及标量ε>0使得下列不等式成立：

(13)

Πij+Πji<0,i=1,2,…r,j≤i。

(14)

其中

(15)

式(14)中

则闭环系统(11)渐近稳定。

证明构造Lyapunov-Krasovskii泛函如下：

(16)

其中，P>0,Q0>0,Q1>0,R0>0,R1>0。

对V(t)沿着闭环系统(11)关于时间t求导，得

xT(t)Q0x(t)+xT(t-τm)(Q1-Q0)

x(t-τm)-xT(t-τM)Q1x(t-τM)+

fT(x,t)f(x,t)。

(17)

由Jensen’s不等式，得

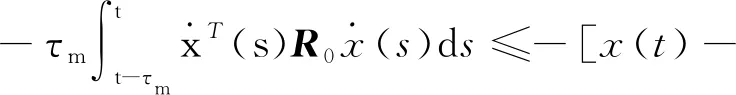
(18)

根据引理1，得

(19)

其中

根据引理2，得

(20)

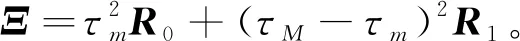
于是，由式(17)～(20)，得

(21)

其中

利用Schur补，得

(22)

其中

因此，如果下列不等式成立

Πij+Πji≤0,i=1,2,…r,j≤i。

(23)

则下面式子成立：

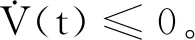
即闭环系统(11)是渐近稳定的，即定理1证毕。

注意到，定理1中，由于非线性项PBKj的存在，矩阵不等式(14)中的增益矩阵Kj无法通过MATLAB中LMI工具箱直接求解。因此，我们给出以下定理。

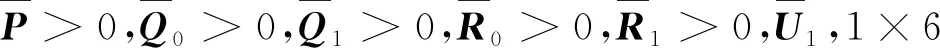
(24)

(25)

其中

(26)

式(26)中：

证明：令

对式(13)左边矩阵分别左乘J1和右乘其转置矩阵可得(24)，对式(14)左边矩阵分别左乘J2和右乘其转置矩阵得

(27)

其中

(28)

注意到，-PΞ-1PT≤-2εP+ε2Ξ，以及对式(28)左边矩阵分别左乘J3及右乘其转置矩阵，可得式(26)，即定理2证毕。

3 数值仿真

为了验证本文提出的网络化模糊控制策略的有效性，我们针对受非线性自激波浪力影响的海洋平台，设计了六种网络化模糊控制器(NFCs)，分析所设计的控制器对平台第一层、第二层和第三层位移响应的减振效果，并和文献中已有的控制器如积分滑模控制器、动态输出反馈控制器进行了比较；最后还分析了网络诱导时滞对海洋平台系统性能的影响。

3.1 系统参数

根据文献[11]，图1中平台的相关参数取值如下：海洋平台第一和第二振动模态的阻尼比为ξ1=ξ2=0.005，结构参数分别为φ1=-0.003 445和φ2=0.003 446 28，平台两个模态固有频率的摄动方程分别为：

ω1=(1.818+0.1sin(t))r/s，ω2=(10.868 3+0.1sin(t))r/s。

选取4条模糊规则，并给定平台两个模态固有频率的模糊集分别为ω1={1.718，1.918}和ω2={10.768 3，10.968 3}。调谐质量阻尼器的质量mT=469.483 6 kg，阻尼比ξT=0.15，固有频率ωT=1.818 r/s，阻尼CT=256 Ns/m和刚度KT=1 551.5 N/m。根据上述参数的取值，海洋平台的系统矩阵Ai,B,和D分别为：

3.2 网络化模糊控制器效果分析

假设网络诱导时滞在τm=0.03 s与τM=0.04 s之间变化，令采样周期为h=0.1 s，μ=0.26和ε=10，根据定理2，利用MATLAB中LMI工具箱进行求解可得控制增益矩阵Kj(j=1,2,3,4)为：

于是，我们得到了网络化模糊控制器(NFC)。将该控制器作用于海洋平台上，图3至图5分别是平台的第一层、第二层和第三层的位移响应曲线图，图6是平台所需的控制力曲线图。事实上，容易计算得到，在NFC作用下，海洋平台的第一层、第二层和第三层位移幅值分别从无控制情形下的1.373 8 m，1.488 9 m和1.563 4 m降低到了0.196 3 m，0.216 5 m和0.233 0 m，海洋平台三层位移的平均幅值降低了85.4%，所需的最大控制力为1.088 0×105N。从上述图形和计算结果可以看出，我们设计的网络化模糊控制器NFC能够有效降低海洋平台位移的振动幅值，从而提高平台的安全性。

图3 海洋平台的第一层位移响应曲线Figure 3 Response of the first floor of the offshore platform

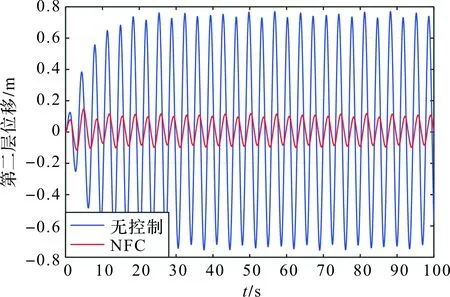
图4 海洋平台的第二层位移响应曲线Figure 4 Response of the second floor of the offshore platform

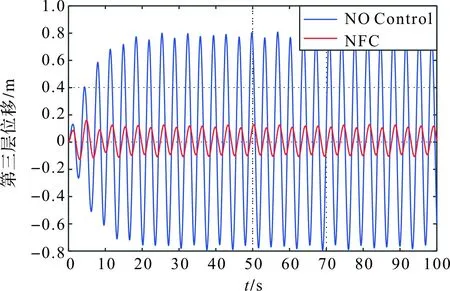
图5 海洋平台的第三层位移响应曲线Figure 5 Response of the third floor of the offshore platfor

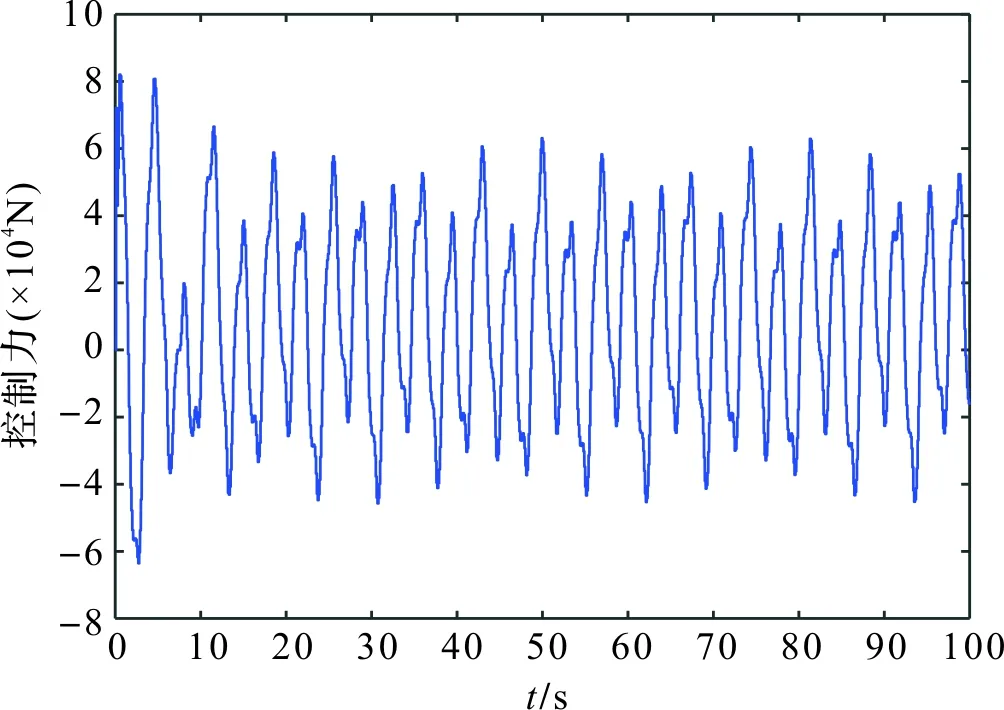
图6 NFC作用下控制力曲线Figure 6 Curve of the control force under NFC

3.3 不同控制方法比较

为了说明本文提出网络化控制方法的优越性，我们将本文设计的网络化模糊控制器(NFC)与动态输出反馈控制器(DOFC1)[23]和积分滑模控制器(ISMC)[24]分别从海洋平台的位移减振幅值和平台所需的控制力大小两个方面进行了比较。

表1给出了在无控制、NFC、ISMC和DOFC的作用下，海洋平台的第一层、第二层和第三层位移的振动幅值以及所需的控制力大小的值。从表1中我们可以看出，与ISMC和DOFC相比，本文提出的网络化模糊控制器(NFC)对平台具有更好的减振效果，且所需的控制力更小。

表1 海洋平台系统三层位移振动幅值和控制力值

3.4 网络诱导时滞对系统性能的影响分析

假设网络诱导时滞τ(t)在区间[τm,τM]之间变化，为网络诱导时滞对系统性能的影响，我们给定了不同的时滞下界τm和时滞上界τM，并设计了若干个相应的网络化模糊控制器(NFC)。在这些不同的模糊控制器作用下，我们分别研究了系统的减振效果。

下面给出了6个网络化模糊控制器以及对应的时滞下界和上界值τm和τM：

其他参数的取值同3.2节。将相应的控制器分别作用于海洋平台上，我们计算得到了平台的第一层、第二层和第三层的振动幅值以及平台所需的最大控制力值，其值由表2给出。不难发现，所设计的NFCs可以分为3类，分别为NFC1；NFC2和NFC4；NFC3，NFC5和NFC6。这三类控制器分别将平台三层位移的平均幅值降低至24.0%，16.1%和14.7%。由此可见，不同的网络诱导时滞下界和时滞上界对系统的性能产生了不同的影响。

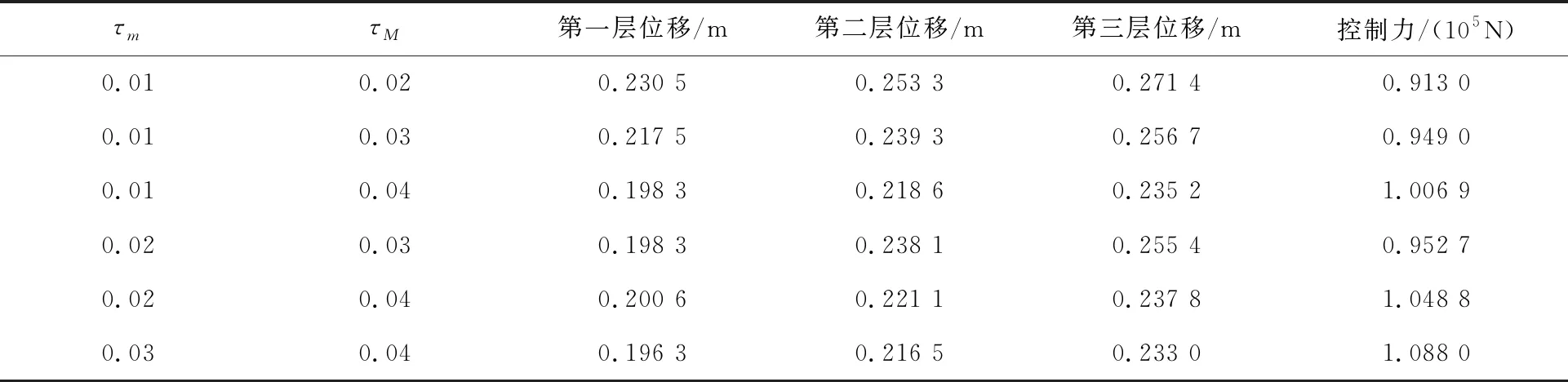
表2 在不同控制器NFCs作用下系统三层位移振动幅值和控制力值

下面我们研究在NFC1作用下，时滞下界固定以及时滞上界逐渐增大时控制器对平台的性能影响，其相应的系统性能指标值由表3给出。从表3中，我们可以发现在NFC1作用下，当网络诱导时滞的下界给定为s，时滞的上界从0.02 s增加至0.05 s时，NFC1的减振效果更加明显，但同时需要的控制力有所增加，从这一方面可以看出小时滞对系统性能的正面作用；但当时滞的上界为0.06 s时，海洋平台的三层位移有相对较大的振动幅值并大于无控制时的位移，也意味着该控制器不再适应本平台，平台处于不安全的环境中。

表3 在NFC1作用下，时滞上界变化时系统三层位移振动幅值和控制力值

基于上面结果可以看到，本文所设计的网络化模糊控制器(NFC)有效地降低了海洋平台的振动幅值，并将平台三层的平均位移降低至14.6%；与积分滑模控制器(ISMC)和动态输出反馈控制器(DOFC1)相比，网络化模糊控制器对平台具有更好的减振效果，且所需的控制力更小；同时，网络诱导时滞对系统的性能产生了不同的影响，说明选择合适的网络诱导时滞对网络化模糊控制器的设计至关重要。

4 结 语

本文针对受到非线性自激波浪力作用的钢结构海洋平台，建立了海洋平台系统的网络化T-S模糊模型，给出了网络化模糊控制器的设计方法，运用Lyapunov-Krasovskii泛函方法得到了闭环系统渐近稳定的充分条件。仿真结果验证了本文所设计的网络化模糊控制器能够有效地降低海洋平台的振动幅值，提高海洋平台的安全性。