外形及工况参数对轴承柔性保持架动力学性能的影响*

张 航，雷学林，何 云

(华东理工大学 机械与动力工程学院·上海·200237)

0 引 言

发展长寿命、高精度、敏捷机动的卫星技术一直是我国的重大战略需求。动量飞轮是保障卫星平台高可靠性服役性能的核心零件。动量飞轮利用动力矩定理决定卫星姿态和控制效果。凭借控制精度高和耗电低的优势，其已被广泛应用于卫星姿态控制领域[1]。然而，在快速机动、连续过零工况的运行下，动量飞轮的失效情况时有发生，严重威胁到了卫星平台的服役性能。仅2016年，我国的2颗在轨卫星的3台反作用飞轮就出现了工作电流增大的异常现象。除此之外，在轨服役超过5年的动量飞轮产品也陆续暴露出了转速响应异常和卡滞等问题[2]，原因为保持架失稳、润滑油碳化、油泥增加等导致轴承组件的摩擦性能下降、阻力矩增大。

由此可见，高精度滚动轴承是动量轮的核心组件，而保持架作为轴承组件的关键结构件，在保证空间执行机构轴承组件长寿命、高可靠的工作中起着重要作用。随着工业技术的迅速发展，卫星产品对轴承转速、旋转精度等性能的要求越来越高。在过零动量轮高速工作期间，保持架失稳会使轴承产生不稳定的振动，发出啸叫，同时导致保持架与滚动体、挡圈的碰撞频率增高，摩擦磨损加剧，甚至引发断裂失效[3-7]。因此，开展针对高速滚动轴承的瞬态特性及动态性能的研究，理清轴承的最优使用工况条件，进而优化高速轴承的设计，对提升轴承组件的使用性能和保障动量飞轮的长时间、高可靠性运行而言十分重要。

自20世纪70年代以来，滚动轴承的动态性能已长期成为研究的热点与难点。Walters首次建立了球4自由度、保持架6自由度的球轴承动力学仿真模型，确立了滚动轴承保持架动力学的分析基础[8]。Jones在简化了轴承滚动体与滚道润滑机制及假定保持架为刚性体的前提下，通过分析获知保持架与套圈之间的摩擦力会驱动保持架的涡动，且外圈旋转时涡动方向与保持架的自转方向相同，内圈旋转时涡动方向与保持架的自转方向相反。Gupta[9]通过分析滚动体与滚道，保持架与滚动体、套圈挡边之间的相互作用，建立了全6自由度的滚动轴承完全动力学模型。该模型可以模拟时变工况下轴承零件的瞬态运动特性，并且通过研究得到了工况、加工参数、摩擦为保持架稳定工作的三个主要影响因素。三因素间相互耦合，是轴承性能优化的有效途径。Weinzapfel和Ashtekar[10-11]将保持架设为有限元组成的柔性体，建立了柔性保持架的轴承动力学分析模型。分析发现，柔性保持架可显著降低轴承进入平稳运转的时间，减小滚动体与保持架之间的碰撞力。Nogi[12]在不考虑热效应和径向载荷的前提下，借助Gupta模型，经分析得出由滚动体与保持架的摩擦引起的高频涡动是导致保持架失衡的主要原因，同时提出判定保持架稳定性的依据为保持架的临界摩擦系数。在建立了轴承动力学分析模型之后的几十年里，国外不断发展出BRAIN、CYBEAN、BEAST等轴承动力学仿真软件[13-15]，实现了接近实际工况下的对保持架工作的仿真。国内学者对滚动轴承动力学的研究始于上世纪90年代，对保持架动态特性的研究主要基于两种方式，研究较早的方式基于Gupta开发的滚动轴承动力学分析模型。叶振环[16]考虑到润滑油对滚动体的阻滞力矩，分析了不同外载荷下保持架的打滑率和不稳定性，为轴承—转子系统的可靠性和稳定性增长研究奠定了基础。DONG[17]基于弹性流体动力润滑理论研究了滚动体和保持架之间的法向接触力，经分析得到了弹性流体动力的润滑作用随负载增加而逐渐降低的结论，另一种是基于有限元软件为平台进行仿真分析。崔立等[18]通过ANSYS显示动力学方法分析了保持架的应力分布和动态响应，得到了保持架应力最大处及兜孔游隙对保持架动态性能的影响。

可见，在现阶段的国内外研究中，大多数研究者建立的滚动轴承动力学分析模型均将保持架视为刚性体，仅考虑了其在工作时的弹性变形。然而，航天系统轴承的过梁与侧梁均较薄，且轴承多采用多孔高分子材料，上述因素使得保持架的柔性较高。同时在相关研究中，针对轴承刚柔耦合模型中柔性保持架动态性能的最佳工作参数和外形尺寸的分析还鲜有报道。因此，本文以在太空条件中工作的深沟球轴承为研究对象，利用ADAMS/View平台建立了滚动轴承动力学模型，采用正交分析法探讨了工况因素(轴承转速)及轴承系统因素(保持架兜孔形状和保持架厚度)共同作用下的滚动体自转转速、保持架转速及动态接触力的变化情况，并结合保持架质心轨迹及打滑率对保持架的外形尺寸和使用工况进行了优化。

1 滚动轴承动力学分析模型

目前，大多数空间执行机构的活动区域为地球附近。以这部分太空区域为参考，由于没有空气对流传热，执行机构向阳面吸收的太阳热辐射可达100℃，背阳面吸收的太阳热辐射则为零下150℃，形成了极端温度差，故可取-20℃的平均工作温度进行仿真计算。以深沟球轴承16003为研究对象，轴承的外形尺寸及性能参数如表1所示，-20℃条件下轴承的材料参数如表2所示。轴承内外圈均无挡边，轴承引导方式为外引导。

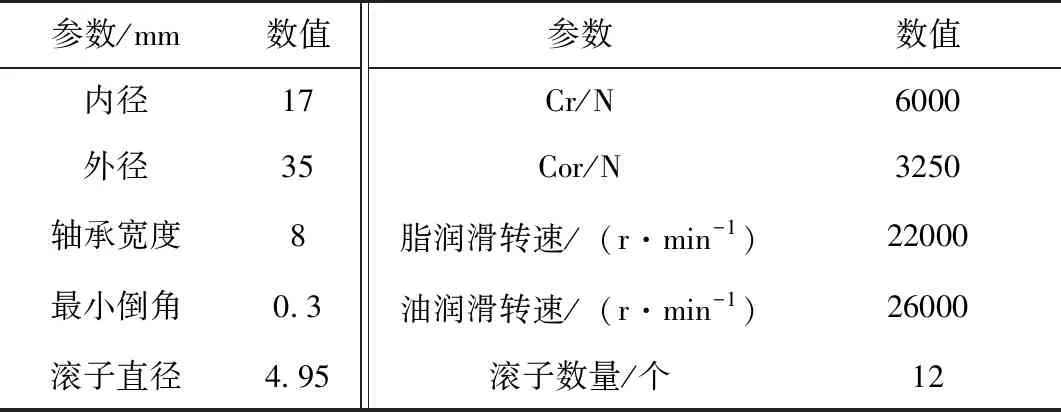
表1 外形尺寸及性能参数Tab.1 Structural and performance parameters

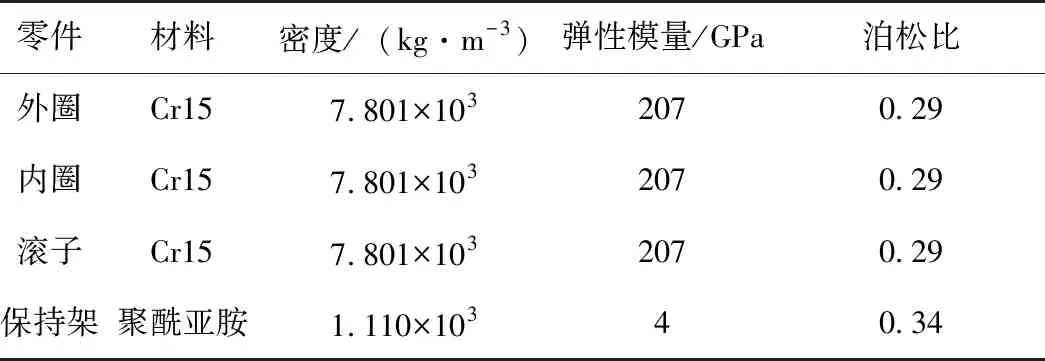
表2 材料参数Tab.2 Material parameters

为减少仿真计算时长，在不影响轴承工作和内部应力的条件下，在建模时可忽略轴承倒角，建立的滚动轴承动力学模型如图1所示。

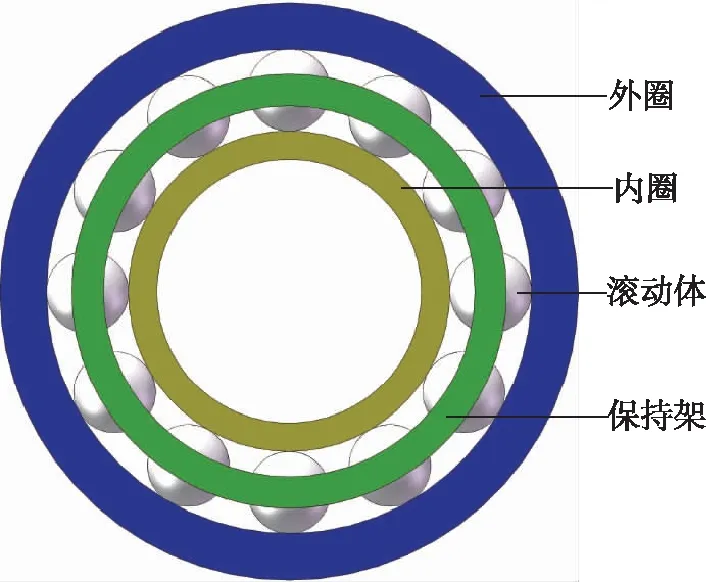
图1 动力学仿真模型Fig.1 Dynamics simulation model

1.1 试验方案设计

为分析工况参数及轴承外形尺寸对保持架动态性能的影响，本次仿真采用三因素三水平L9(34)正交方法，三因素分别是轴承转速、保持架兜孔形状和保持架厚度。每种因素取三个水平，正交试验表如表3所示，部分保持架模型如图2所示。方形兜孔的尺寸为5.02mm×5.02mm，4个倒角r为1.5mm，圆形与球形兜孔的尺寸R为2.51mm，兜孔游隙均为0.07mm。轴承工作方式为内圈旋转、外圈固定。

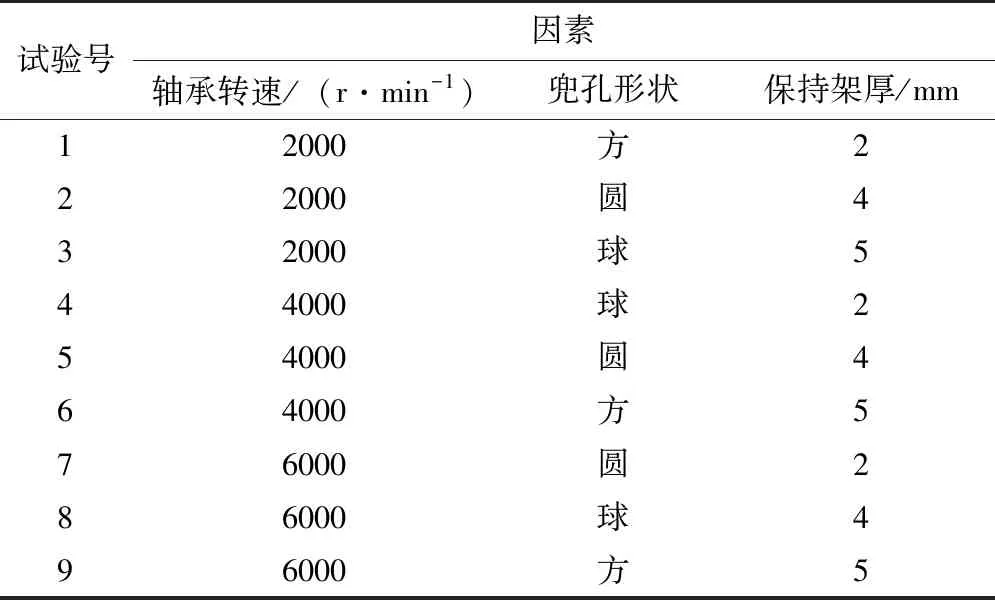
表3 正交试验参数表Tab.3 Orthogonal test parameter table

(a)方形

1.2 动力学模型参数设定

本次模型使用到了两种运动约束，即平移副和旋转副。设定方式为：(1)轴承外圈与大地(ground)建立平移副，此时轴承外圈仅在径向平面有平动自由度；(2)轴承内圈和保持架分别与大地(ground)建立旋转副，作用点为轴承中心。驱动设给内圈与大地(ground)联结的旋转副，转速为不同工况下的内圈转速。

滚动体与内外圈以及保持架之间通过“体—体”接触进行约束。构件接触力采用冲击函数模型(Impact)进行定义，冲击函数法可以建立连续速度场和位移量，进而可定义间隙构件之间的接触力。冲击函数法较另一种恢复系数法通用性更强，且计算更为准确。冲击函数法的参数设定为，Hertz刚度系数K为(1×105)11/5(N/mm)，碰撞指数e为11/5，阻尼系数C为10，阻尼系数达到最大时的穿透深度d为0.1mm。动态摩擦力由Coulomb摩擦模型计算，摩擦力等于正压力乘以摩擦系数(f=F·μ)。通过查阅轴承手册，可确定静摩擦系数μs为0.1，动摩擦系数μd为0.1，静平移速度vs为10(mm·s-1)，动平移速度vd为50(mm·s-1)。

Adams/Slover提供了多种积分器，本次使用了仿真速度快、位移精度高的GSTIFF积分器。该积分器有两种积分格式：I3和SI2。I3求解器的求解速度快但误差高，因此本文采用了SI2求解器。

2 轴承动力学仿真结果

2.1 工况参数对轴承组件转速波动的影响

工作载荷和转速是轴承工况中最为重要的两个变量，本文主要研究了在工作载荷一定时，转速对轴承动力性能的影响。图3为在轴向预载荷为50N的条件下，保持架和滚动体在九种试验条件下的转速波动标准差。k1-k3、RA-RC分别为保持架公转转速及轴承内某一滚子的自转转速在三水平情况下的标准差均值和转速标准差均值的极差值。标准差均值越小，转速波动越平稳。

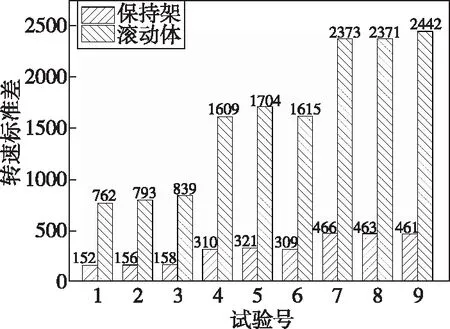
图3 保持架和滚动体转速波动结果分析Fig.3 Analysis of cage and roller speed fluctuation

当轴承转速由2000r/min增大到6000r/min时，保持架转速标准差由k1(155.1)增大到k3(463.0)，增长率为299%，保持架转速的稳定性显著降低。保持架的转速波动性在其厚度为2mm和5mm时相差不大，均小于厚度为4mm时的转速波动性，这说明随着保持架厚度的增加，其转速稳定性先降低而后升高。当兜孔形状分别为圆形、球形、方形时，保持架的转速稳定性逐渐降低。极差值RA为307，RB为4.4，RC为1.1，且有RA>RB>RC。这说明该因素对保持架转速影响的由主到次的顺序依次为A、B、C，即内圈转速的影响最大，其次为厚度，而兜孔形状的影响最小。为提高保持架在工作时转速的平稳性，需按照标准差均值大小选取优组合，即选取保持架厚度为2mm，兜孔形状选用圆形兜孔，选取轴承转速为2000r/min。

当轴承内圈的转速为2000r/min时，滚子的转速稳定性最好。随着轴承内圈转速的增加，滚子的转速波动性显著，保持架转速标准差由k1(798.0)增大到k3(2395.5)，稳定性降低了近200%。滚子的转速稳定性与保持架厚度呈反比关系。当兜孔形状分别为圆形、球形、方形时，滚子转速稳定性逐渐降低。极差值RA为1597.5，RB为50.8，RC为42.7，且有RA>RB>RC，说明轴承转速对滚子转速的影响最大，位列第二的影响因素为保持架厚度，最后的影响因素为兜孔形状。为减小滚动体自转的转速波动，提高轴承的工作平稳性，需按照标准差均值大小选取优组合，即选取保持架厚度为2mm，兜孔形状选用圆形兜孔，选取轴承转速为2000r/min。

2.2 工况参数对保持架接触力的影响

滚动轴承各零件之间的动态接触力是影响轴承运行质量和寿命的重要因素，也是轴承设计需考虑的关键因素之一。图4为在轴向预载荷为50N的条件下，保持架和滚动体在九种试验条件下的平均接触力。k1、k2、k3分别为三水平情况下保持架平均接触力的均值，R为三个水平下平均接触力均值的极差值。

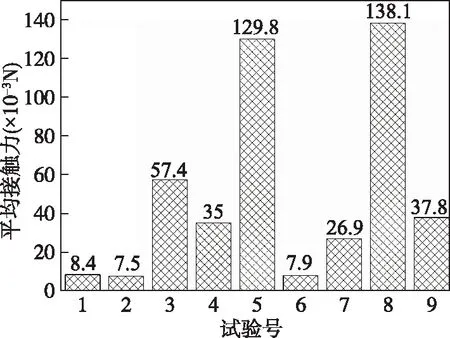
图4 保持架平均接触动态力Fig.4 Average dynamic contact force of cage

当轴承转速由2000r/min增大到6000r/min时，保持架接触力均值由k1(2.4×10-3)增大到k3(6.76×10-3)，这说明保持架平均接触力逐渐增加。厚度为4mm的保持架平均接触力远大于其厚度为2mm和5mm时的平均接触力。这说明随着转速增加，保持架接触力先增高后降低。当兜孔形状分别为圆形、方形、球形时，保持架平均接触力逐渐升高。极差值RA为3.3×10-3，RB为6.8×10-3，RC为6.3×10-3，RB>RC>RA，说明保持架厚度对保持架接触力的影响最大，其次的影响因素为兜孔形状，轴承转速的影响最低。保持架接触力越高，载荷越会呈现出明显的冲击特性，加速保持架横梁疲劳断裂的进程。因此，为降低保持架与滚动体之间的接触力，需对保持架接触力选取优组合，即选取保持架厚度为2mm，兜孔形状选用圆形兜孔，选取轴承转速为2000r/min。

2.3 保持架的质心轨迹

图5为九种试验条件下保持架的质心轨迹。由图5可以看到，当兜孔形状为方形时，保持架的质心轨迹接近于“筒状”，可以保持稳定的工作轨迹；球形兜孔保持架的轴向窜动最小，说明侧梁与滚子的碰撞频率最低，有助于轴承稳定运转；圆形兜孔保持架的质心轨迹最为紊乱，稳定性差。

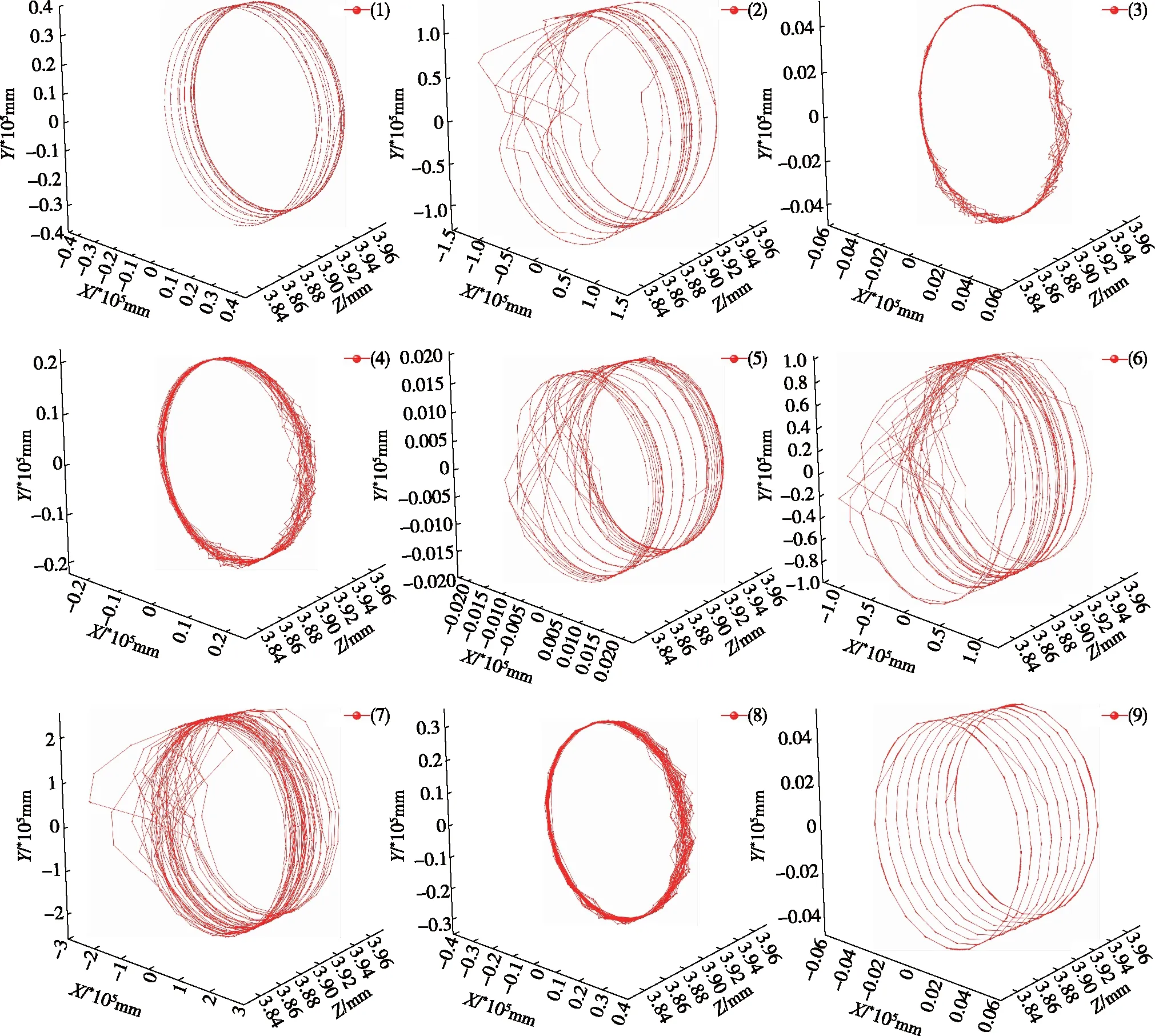
图5 保持架的质心轨迹Fig.5 Cage mass center orbit

将保持架轨迹半径进行拟合处理，可得三因素极差，且有RC>RB>RA。这说明兜孔形状对保持架涡动半径的影响最大，随后的影响因素是保持架厚度，影响最小的因素是轴承转速。保持架工作区域的缩小可以避免保持架过梁与滚子的偏心碰撞，因此可针对保持架接触力选取优组合，即选取保持架厚度为5mm，兜孔形状选用方形兜孔，选取轴承转速为4000r/min。

2.4 打滑率

保持架的打滑率反映了其理论转速与实际转速的差值。打滑率越小，说明保持架的理论转速与实际转速越接近，滚动体在滚道内发生的滑动摩擦越少，保持架的工作越稳定。保持架的理论转速为

式中，na为外圈转速；nb为内圈转速；DZ为滚子直径；DpZ为滚子节圆直径；α为滚动体的接触角。对于本文轴承外圈固定的工作条件，保持架的打滑率S为

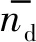
通过对比9次试验可知，保持架打滑率随转速升高而升高。这是由于随着内圈转速升高，滚子公转速度升高，从而带动保持架的公转速度升高，保持架的偏心运动加剧。与此同时，滚子的离心力增大，两者的共同影响使得保持架打滑率增加，不利于轴承性能的维持。三因素的极差比较结果为RA>RB>RC，这说明转速对保持架打滑率的影响最大，其次的影响因素为保持架厚度，影响最小的因素为兜孔形状。为降低保持架打滑率，需选取优组合，即选取保持架厚度为2mm，兜孔形状选用方形兜孔，选取轴承转速为2000r/min。

本文得到的保持架公转转速和滚子自转转速与文献[19]所得的转速曲线的变化趋势基本一致；保持架质心轨迹与文献[19]所测得的空间轨迹相吻合；柔性保持架与滚动体的动态碰撞力与文献[7]所得结果的数量级一致，数值也较为接近。以上对比验证了本文模型与结果的正确性及可靠性。

3 结 论

利用动力学仿真模型实现了对深沟球轴承柔性保持架的动态性能分析，选取正交试验法分析了不同转速下轴承保持架的模态分析、转速波动、接触力、保持架质心轨迹和打滑率，并得出了如下结论：

(1)当轴承转速由2000r/min增大到6000r/min时，保持架与滚子转速的稳定性均降低了约200%。当兜形分别为圆形、球形、方形时，保持架与滚子转速的稳定性均逐渐降低；随着轴承内圈转速的提高，保持架与滚子之间的平均动态接触力增大，碰撞频率升高，冲击载荷升高，打滑率随之上升；在轴承工作时，保持架质心轨迹接近“筒状”；

(2)保持架厚度对保持架和滚子运转平稳性、接触力等方面的影响大于兜孔形状。厚度越大，保持架工作越平稳。当横梁与滚子之间的接触力增加时，会发生高频轻微碰撞，加剧疲劳磨损。保持架质心轨迹受兜孔形状的影响最为明显，选用方形兜孔和增大保持架厚度可以有效减少保持架质心的活动范围，确保轴承平稳工作；

(3)为更好地满足动量轮轴承组件对长寿命、高可靠性的需求，综合考虑了动态性能及各自占比：转速波动(15%)、接触力(35%)、质心轨迹(25%)、打滑率(25%)，得到最优工况及设计方案为：轴承转速为2000r/min，保持架为方形兜孔，厚度为2mm。