基于数据驱动的非合作航天器姿态估计与预测方法*

陈 航，陈敏花，蒋催催，郇文秀，潘 菲，胡庆雷

(1.北京航空航天大学 自动化科学与电气工程学院·北京·100191；2.上海航天控制技术研究所·上海·201109)

0 引 言

近年来，临近操作已成为航天领域中的重要研究方向，也是各个国家的重点工程项目之一，其主要包括在轨相对观测与监视、在轨燃料补给，以及在轨组装[1]等。在典型非合作场景中，相对姿态确定是重要且困难的任务之一，也是完成其他任务的重要基础。一方面，由于目标非合作特性和微小卫星对容纳载荷体积的限制，无法实现可靠的相对角速度测量。在这种情况下，如何在缺少角速度测量的情况下完成对相对姿态的确定，是一个关键问题；另一方面，由于太空环境光照[2]等不确定因素和末端执行机构对视觉传感器的遮挡[3]，目标航天器的观测校正信息无法及时被获取，需对目标姿态进行预测，以保障后续任务执行的安全可靠。因此，在姿态确定中考虑一种新型、有效的航天器姿态估计与预测方法，处理上述两个问题，具有重要的工程实际意义。

卡尔曼滤波算法(Kalman Filter,KF，以下简称KF算法)被广泛应用于各类航天器的姿态确定任务中。KF算法通常可分为扩展卡尔曼滤波器[4](Extended Kalman Filter,EKF)、乘性扩展卡尔曼滤波器[5](Multiplicative Extended Kalman Filter,MEKF)和其他方法[6]。在Lefferts等[7]提出的MEKF算法中，算法采用陀螺仪测量模型确定角速度。Filipe等[8]继承并提出了对偶角速度测量模型。但是，在非合作背景下，信息无法交互，也无法传递角速度信息，上述方法无法满足任务要求。此外，为精确估计目标航天器的角速度，转动惯量也是需要获取的关键参数之一。Psiaki[9]提出了一种基于最小二乘的方法，以估算航天器姿态动力学的相关参数。在Yoon等[10]提出的姿态参数校准卡尔曼滤波算法中，除航天器的姿态和角速度外，算法还考虑了航天器和飞轮转动惯量的估计。Xu等[11]提出了一种采用序列图像进行惯性参数估计的方案。Setterfield[12]提出了使用本体极迹分析来估计转动惯量的算法，但只考虑了主轴转动惯量。上述文献均未考虑视觉导航中存在的惯量积估计问题。因此，在缺少角速度测量信息的情况下估计完整转动惯量矩阵，是一个亟待解决的问题。

视觉导航算法在非合作任务中广受青睐，而另一个挑战则来自于由视觉特征遮挡而导致的目标航天器跟踪姿态信息的丢失。Yu等[13]为空间机器人开发了一种融合触觉反馈和视觉观测的框架，以解决目标跟踪和定位问题。Cheung等[14]考虑到视线遮挡，设计了一种视觉目标运动估计算法，但该算法仅能处理地面运动物体，对空间翻滚航天器不适用。闫谦时[15]利用最小描述长度准则和贝叶斯估计方法确定了时间序列预测模型的阶数和参数，对航天器遥测数据的趋势变化进行了预测。但是，该方法的长期预测精度较低。由于没有可用的校正信息，姿态预测问题的实质是求取姿态运动的解析解。航天器姿态运动学为强非线性函数，其微分方程不具有解析解。采用传统数值积分方法能够实现短时间内的较高精度预测，但是由于随时间累积的误差，此类方法同样不适用于较长时间内的姿态预测。

针对上述问题，本文设计了一种乘性扩展卡尔曼滤波方法，通过将转动惯量的相对比值增加到滤波状态量中，实现了对完整转动惯量矩阵比值的估计，提高了姿态和角速度估计的精度，并且无需获取角速度测量信息；然后，分别基于函数拟合和神经网络，设计了两种预测方法，实现了较长时间内对目标航天器姿态的预测。本文结构安排如下：在第1节介绍了非合作航天器的姿态动力学和视觉导航问题；在第2节给出了基于MEKF的姿态和参数估计算法；在第3节设计了函数拟合和神经网络两种姿态预测方法；在第4节，通过数值仿真验证了滤波估计算法和姿态预测算法的实时性和准确性；在第5节得出了结论。

1 非合作航天器的视觉导航问题

如图1所示，将依据视觉观测建立的目标航天器坐标系定义为FL={XL,YL,ZL}，将追踪航天器本体系定义为FB={XB,YB,ZB}。

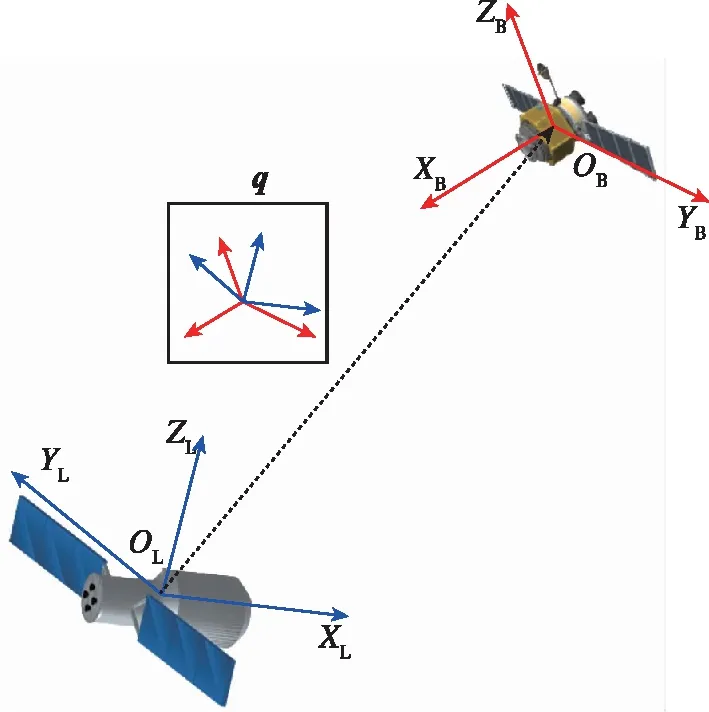
图1 相对位姿确定问题的示意图Fig.1 Schematic diagram of relative attitude

假定FB为惯性系，并定义从坐标系FB到FL的姿态四元数为q，则本文采用四元数描述目标航天器姿态运动学和动力学，具体如下

(1)

(2)

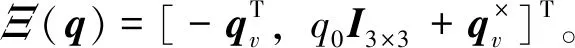
qTq=1

(3)

本文所使用的四元数运算定义如下：

四元数乘法

(4)

共轭

(5)

ω=[ω1,ω2,ω3]T，为目标航天器本体系相对惯性系的角速度，并被表示在追踪航天器本体系下。但是，目标航天器本体系在视觉导航中不是先验已知，转动惯量主轴不一定与通过视觉观测建立的目标航天器坐标轴重合。此时，其转动惯量矩阵J不是对角矩阵，即惯量积不为零。

(6)

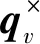
(7)

外部扰动力矩τ由重力梯度力矩、磁力矩、太阳光压力矩等组成，可建模为高斯白噪声。

文献[10]指出，在视觉导航的任务场景中，目标航天器转动惯量的真实值并不能从相对姿态测量中获得。因此，本文设计了滤波算法，以估计转动惯量的相对比值。从原理来看，转动惯量矩阵中的六个独立元素均可作为基准。本文选取其中的Jxx，并将式(2)改写为如下形式

(8)

其中，J′定义为转动惯量的相对比值矩阵

(9)

目标航天器姿态确定的过程仅用转动惯量的相对比值便可实现。只需采用合适的估计算法，转动惯量矩阵的剩余元素J5=[Jyy,Jzz,Jxy,Jxz,Jyz]便可收敛到各项相对于Jxx的比值。

2 基于乘性扩展卡尔曼滤波算法的姿态与参数估计算法

本节不涉及视觉姿态解算，同时假定可获得相对于追踪航天器的目标航天器的相对姿态测量量。

定义目标航天器的误差状态量如下

(10)

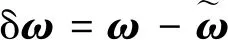
(11)

(12)

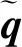
将刚体航天器动力学(2)代入误差角速度的定义式(11)，得到

(13)

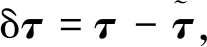
(14)

依次考虑上式相对各状态量的雅可比矩阵

(15)

(16)

(17)

其中，对任意三维向量a，矩阵χ5(a)定义如下

文献[7]给出了误差四元数矢量部分的状态方程

(18)

卡尔曼滤波的状态方程为

(19)

式中，x(t)为状态变量，F(t)为系统状态矩阵，w(t)为系统过程噪声，G(t)为系统噪声矩阵。

结合公式(15)、公式(16)、公式(17)和公式(18)，可推导乘性扩展卡尔曼滤波的状态方程

(20)

其中

(21)

(22)

(23)

(24)

ητ、ηJ5分别对应δω、δJ5的过程噪声向量。

然后，计算状态转移矩阵Φ

(25)

其中，Δt为离散化时间间隔。

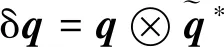
Z(t)=Hx(t)+v3(t)

(26)

其中，H=[I3×3,03×3,03×5]为测量矩阵，v3(t)为测量噪声。

乘性扩展卡尔曼滤波器的建立分为状态一步预测、滤波观测量计算、滤波更新和姿态校正四个部分，具体步骤如下：

(1)状态一步预测

(27)

(28)

(2)滤波观测量计算

根据目标航天器姿态四元数的观测值和预测值，计算姿态误差四元数

(29)

(3)滤波更新

Pk|k-1=ΦPk-1ΦT+Qk-1

(30)

Kk=Pk|k-1HT(HPk|k-1HT+Rk)-1

(31)

(32)

xk=xk-1+Kk(δqv,k-Hxk-1)

(33)

其中，Pk|k-1为k时刻最优预测估值误差协方差阵；Pk-1为k-1时刻最优滤波值误差协方差阵；Kk为k时刻增益矩阵；Qk-1为k-1时刻系统噪声方差矩阵；Rk为测量方差矩阵。

(4)姿态校正

利用范数约束计算误差四元数，并校正姿态

(34)

3 无控翻滚航天器的姿态预测算法

完成滤波后，根据对目标姿态的实时估计结果，本节设计了函数拟合和神经网络两种方法，在没有校正信息的情况下，实现了在未来一段时间内对非合作目标姿态的精确预测。

3.1 基于函数拟合的方法

拟合曲线基函数，直接影响拟合效果。观察图2中姿态四元数的各分量波形，其周期性特征和规律特征比较明显。

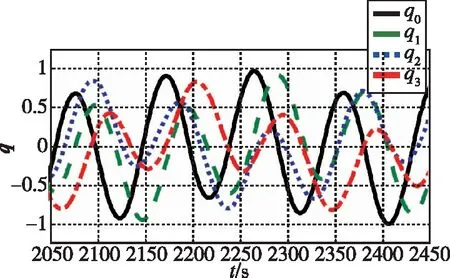
图2 姿态四元数函数波形Fig.2 Estimated attitude quaternion

曲线函数应建立在空间无控翻滚航天器的物理模型基础上，其基本特征应满足如下两个要求：

(1)姿态四元数各个分量均具备类似周期性的特征，其时间曲线围绕0上下振荡，且最大值不大于1，最小值不小于-1。拟合函数和拟合函数的一阶导函数均应为周期震荡；

(2)拟合函数的一阶导函数在数学形式上应与拟合函数保持一致。

考虑将姿态四元数的各个分量拟合为正弦函数和的形式，函数的具体形式如下

(35)

式中，yk为姿态四元数的各个分量；t为时刻；ai、bi、ci均为待确定参数；n为正弦函数项数，拟合效果随项数增加而提升。一般而言，项数为3或4较为合适。采用最小二乘法确定各项参数。

为保证快速收敛，选取滤波最后阶段的姿态数据作为拟合目标。此时，已较好地滤除了过程和观测噪声。姿态四元数标量的拟合效果如图3所示。

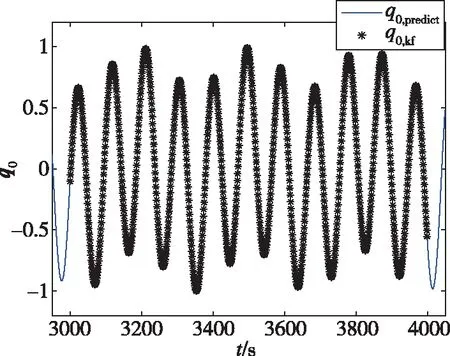
图3 姿态四元数标量的拟合效果Fig.3 Function fitting effect of attitude quaternion scalar term

图3中，黑色曲线为q0,kf，即经滤波处理后的姿态四元数标量曲线，以该曲线为示例进行函数拟合；蓝色实线为q0,predict，即为拟合预测结果，与滤波曲线q0,kf在3000s～4000s内基本吻合。本方法获得了姿态四元数标量的近似函数解析式，可在给定时域以外计算函数值，具备一定的预测能力。

3.2 基于BP神经网络的方法

传统的数值积分方法的预测精度受初始误差影响较大，存在误差随时间累积而带来的稳定性问题，无法满足航天器姿态预测对精度的要求。考虑到临近操作任务对实时性的要求、航天器姿态运动的非线性及其迅速的变化，BP神经网络具备以任意精度逼近任意非线性映射关系的能力，可以用于处理强非线性的刚体姿态运动，训练完成的网络也具备较好的泛化能力。此外，建立BP神经网络，需要足够多、具备代表性的数据，而前期姿态滤波不仅提供了充足的训练样本，也完成了对训练样本的预处理。因此，航天器姿态预测任务适合采用基于BP神经网络的方法。

BP神经网络的训练过程可划分为信号正向传播和误差反向传播两个步骤。在正向传播时，信号的传播沿着输入层—隐含层—输出层的路径，单个神经元只影响与之相连的下一层神经元。通过计算当前输出与期望输出的平方误差函数，判断是否符合期望，若不符合期望，则转入误差反向传播的步骤。随后，依据梯度下降算法，将误差沿反向分摊给各层神经元，并调整网络权值和阈值。上述两个步骤交替进行，直至网络输出误差减小至预设范围。

首先，确定网络选取的层次。分析时刻与预测四元数之间的映射关系，考虑到航天器姿态四元数曲线呈现出的明显的规律性和周期性，选取当前时刻姿态四元数作为输入层神经元，将需要获取的预测四元数作为输出层神经元。由于隐含层神经元数目需要根据多次实验进行最终确定，通过对隐含层不同神经元数目的网络进行对比，可以在兼顾误差和训练时间的要求下确定最佳数目。

使用当前时刻tk的姿态四元数作为神经网络的输入，输出为tk+1000时刻的姿态四元数，并假定完整滤波过程的时长为5000s。训练集不使用未完全收敛的滤波前期1000s的数据，而是选取了1000s～3000s内姿态四元数的滤波估计值。目标输出选取为2000s～4000s姿态四元数的滤波估计值，并搭建了一个结构层数为4-15-4的BP神经网络，即输入层为tk时刻的四元数各分量，输出层为tk+1000时刻的四元数各分量，隐含层节点数为15。其结构示意图如图4所示。

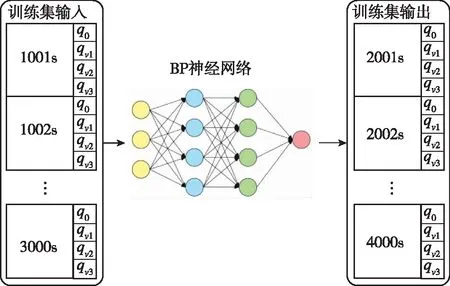
图4 BP神经网络示意图Fig.4 Schematic diagram of BP neural network

此外，由于航天器实际的姿态变化为连续变化，其在任意时刻的观测值均会受到过去观测值的影响。考虑将之前若干时刻的姿态四元数作为输入，分别搭建结构参数为40-70-4和20-40-4的神经网络。前者的输入节点为40个，对应tk至tk-9时刻的姿态四元数，共包含40个参数；输出节点为4个，对应tk+1000时刻的姿态四元数；隐含层节点数目为70个。后者的输入节点为20个，对应当前时刻tk至tk-4时刻姿态四元数的各分量，总计20个参数；输出节点为4个，对应tk+1000时刻的姿态四元数；隐含层节点数目为40个。

4 仿真试验及结果分析

4.1 目标姿态估计

为姿态测量输入加入2度的噪声，采样频率为2Hz。滤波器的参数设置如表1所示。

表1 滤波器的初始参数设置Tab.1 Initialization of the Kalman filter

其中，qnoise=π/90对应姿态输入测量噪声。

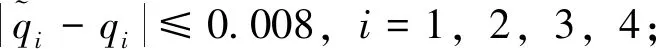
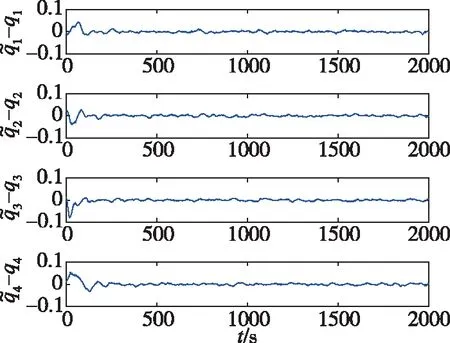
图5 姿态四元数误差曲线图Fig.5 Estimation errors of attitude quaternion

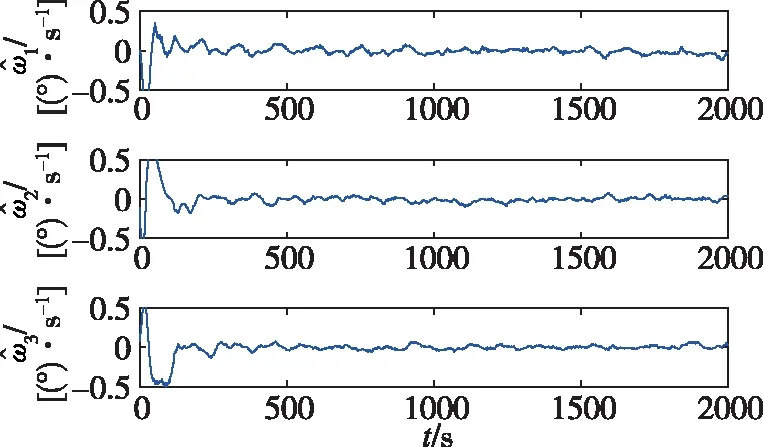
图6 角速度误差曲线图Fig.6 Estimation errors of angular velocity

图7 主轴转动惯量比值估计曲线图Fig.7 Estimation of principal moments of inertia

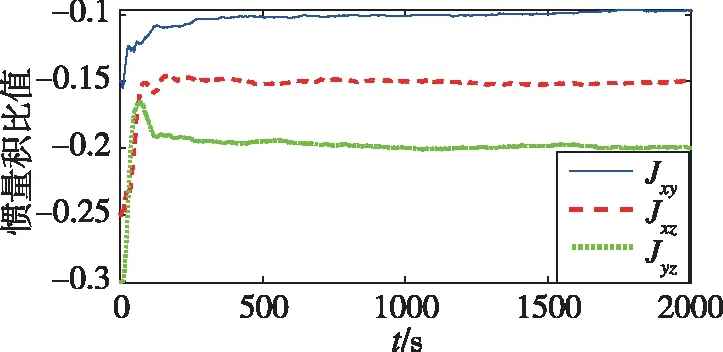
图8 惯量积比值估计曲线图Fig.8 Estimation of products of inertia

4.2 基于函数拟合的姿态预测

滤波估计过程为5000s，选择3000s～4000s内的姿态四元数各个分量曲线，拟合形式为正弦函数之和。由于拟合精度受函数项数影响，为确定最佳项数，绘制项数、拟合结果与原曲线间均方根误差(Root Mean Squared Error,RMSE)的关系曲线如图9所示。

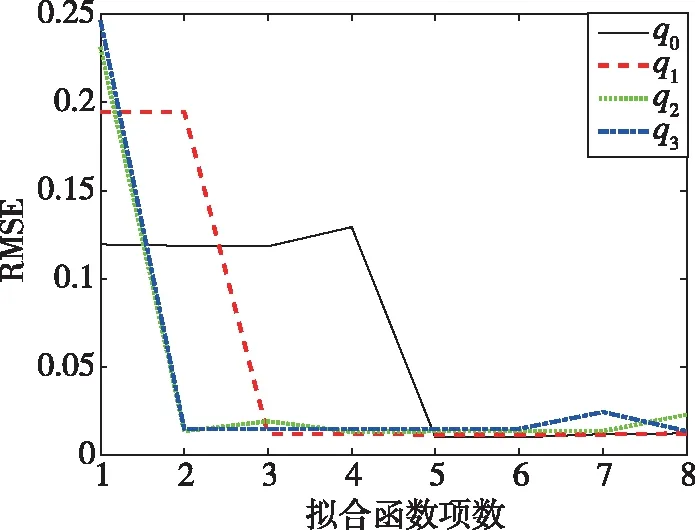
图9 函数拟合项数与均方根误差关系曲线图Fig.9 Relationship between the numbers of terms and RMSE

图9表明，初始时，RMSE会随拟合项数增加而迅速减小，但随后基本未出现变化，部分曲线甚至出现了过拟合现象。为了避免项数过多而导致计算成本增加，选择使均方根误差最小的项数，据此分别确定四元数各分量曲线的拟合项数为8、6、4、2，然后经计算得到各拟合函数在4000s～5000s的函数值。将滤波估计值视为姿态真实值，将误差四元数转为欧拉角，则翻滚、俯仰、偏航角的误差如图10所示。各欧拉角的预测误差分别为2.5670°、3.2009°和2.6242°，且误差与时间无关。

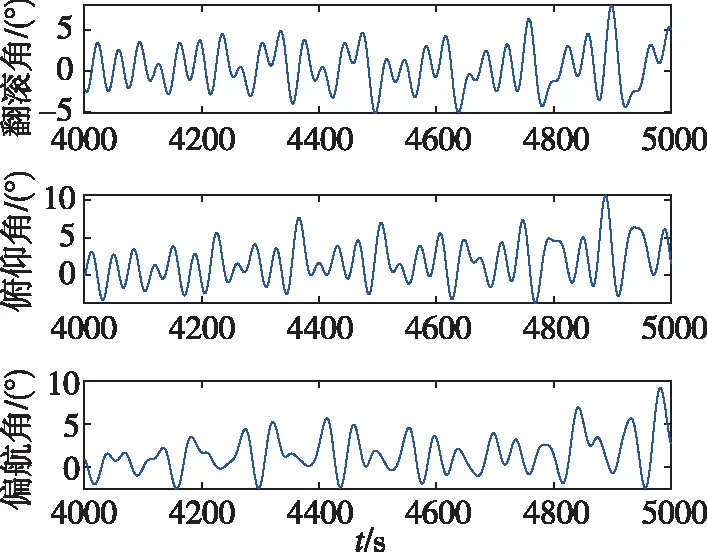
图10 基于函数拟合的姿态预测误差曲线图Fig.10 Prediction errors of attitude Euler angles based on function fitting

4.3 基于神经网络的姿态预测

滤波过程的姿态估计值分为两部分：第一部分(1000s～4000s)为训练数据集；第二部分(4000s～5000s)为验证数据集。在姿态预测过程中，可将滤波估计值视为真实值。将3000s～4000s内姿态四元数的滤波估计值输入训练完成的神经网络，得到4000s～5000s姿态四元数的预测值；随后，将预测四元数与滤波估计四元数间的误差四元数转为欧拉角误差。3.2节所提出的三种结构神经网络的翻滚、俯仰、偏航角误差如表2所示。

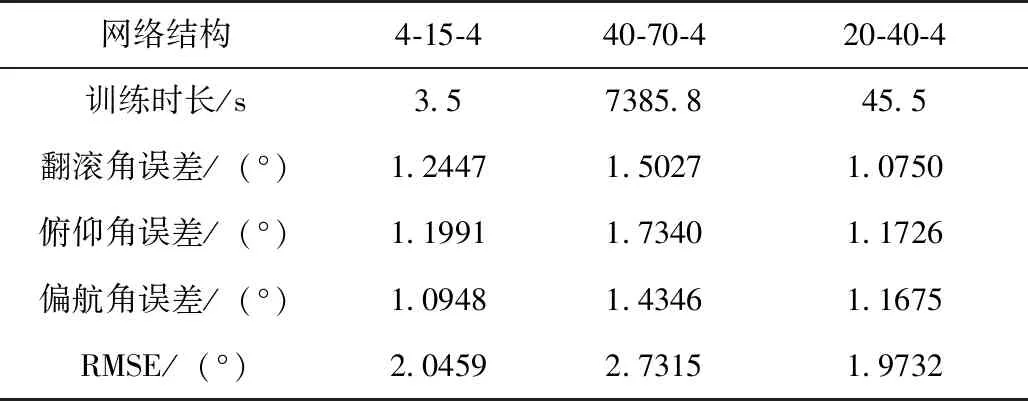
表2 三种不同结构参数的神经网络仿真结果Tab.2 Simulation results of three neural networks

由表2可见，由于节点大幅增加，40-70-4结构的神经网络出现了过拟合现象。相比其他两种结构，其预测误差明显上升。此外，随着网络结构的复杂化，训练计算量和时间也显著增加。该结构与在轨任务对实时性的要求也产生了冲突。20-40-4结构的网络牺牲了一定的时间成本，获得了较高的预测精度，而4-15-4结构的神经网络兼具了高精度和低时间成本的优点。这两种结构的神经网络预测欧拉角误差曲线分别如图11、图12所示。

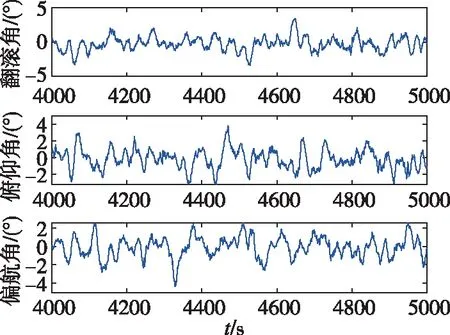
图11 20-40-4结构神经网络的姿态预测误差曲线图Fig.11 Prediction errors of attitude Euler angles of neural network (20-40-4)

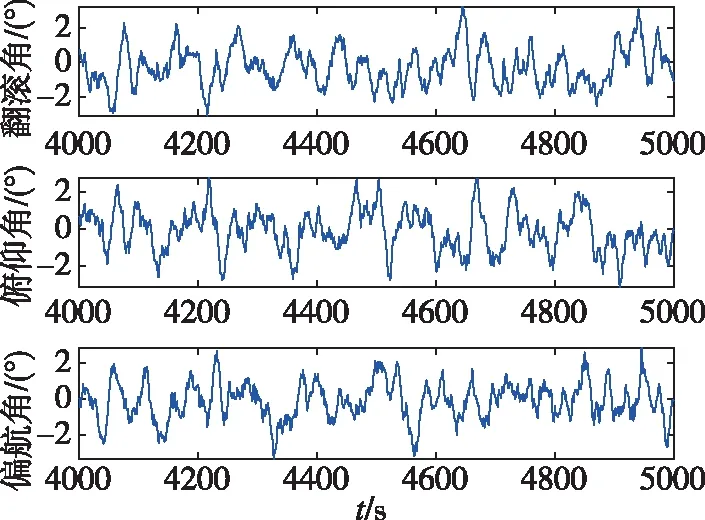
图12 4-15-4结构神经网络的姿态预测误差曲线图Fig.12 Prediction errors of attitude Euler angles of neural network (4-15-4)

图11、图12均显示出了误差与时间无关的良好特性，即预测误差不随时间累积而逐渐增大，一直保持着较高的预测精度，能够满足较长时间内对目标航天器进行姿态预测的要求。此外，以上曲线始终振荡，没有收敛于固定的常值。这是由于预测过程缺少了观测信息、无法校正当前预测值所导致。对比图11与图12可以发现，20-40-20结构神经网络的振荡幅值明显小于4-15-4结构，这与表2的统计结果相符。上述结果表明，在前期，只要能稳定获取空间无控翻滚航天器在一段时间内的姿态信息，即使在丢失跟踪后，仍然能通过本文提出的算法实现较高精度的姿态预测。

5 结 论

本文研究了无角速度测量信息的非合作航天器姿态确定问题，以及缺少校正信息的航天器长时姿态预测问题。将姿态、角速度和转动惯量比值列为状态向量，并基于刚体旋转动力学的差分形式推导了线性化状态方程，提出了一种乘性扩展卡尔曼滤波算法。通过姿态测量校正更新了角速度和惯性参数，避免了需要利用陀螺仪测量信息而带来的限制。针对由末端执行机构遮挡视觉传感器而导致的目标跟踪丢失问题，利用滤波后的姿态数据作为训练样本，分别设计了函数拟合和神经网络两种方法，改善了传统预测方法误差随时间累积的弊端，并提升了姿态预测精度。数值仿真结果表明，滤波算法能够仅使用姿态测量输入而精确估计目标航天器的相对姿态、角速度和转动惯量比值；姿态预测算法能够在长时段内兼顾预测精度和计算速度；本文提出的框架能够实时利用目标航天器姿态信息在线实现较高精度的估计与预测。