基于路径跟随的改进领航-跟随无人机协同编队方法*

胡阳修，贺 亮，赵长春，陈 扬，钱洲元

(1.上海航天控制技术研究所·上海·201109；2.上海市空间智能控制技术重点实验室·上海·201109)

0 引 言

采用集群的方式可以拓展单体无人机的能力，以高效、合作、协同地完成任务。在无人机之间实现相互的功能备份，可以避免由单一无人机失效而造成的任务失败[1-2]。目前，集群无人机协同编队控制方法主要通过位置与速度控制保持相对队形[3]。常用的方法有：基于领航-跟随、基于行为、基于虚拟结构等。基于领航-跟随的方法有着结构简单、对通信容量需求少的优点，在工程实践中的应用较多，国内外学者在此基础上进行了大量的改进研究[4]。

领航无人机通常需要完成全局路径规划，A*算法主要采用了路径搜索算法[5]。文献[6]通过改进A*算法开闭表中的元素存储方式，提升了路径规划效率，但并没有提升路径规划的效果。文献[7]将A*算法与Dubins曲线进行了结合，在起止段采用Dubins曲线，中间采用A*算法，满足了长度最短与安全性的要求。但是，安全性改进只在起点和终点有效，没有考虑全过程的障碍威胁。

跟随无人机通常根据领航无人机的距离与方位信息完成编队跟随。通过将路径信息进行参数化，利用数据链在集群中同步，可以大大提升路径跟踪效果[8]。文献[9]建立了一种基于路径参数协同的多移动机器人编队控制模型，通过建立统一的路径参数，实现了对编队路径的协同，但其所选择的路径参数对于不规则曲线而言不具备较好的普适性。

集群无人机之间的队形协同控制通常采用一致性原理。通过选取无人机的状态信息，设计控制率保持一致[10]。避障是集群系统必须考虑的问题，文献[11]针对无人机编队的机间防碰撞需求，基于人工势场改进防碰撞控制方法，构建了受两者相对运动速度影响的辅助斥力势，并给出了机间防碰撞、障碍物规避的总速度场，但没有考虑动态障碍下的避障优化问题。

综上所述，针对上述研究中存在的问题，本文在领航-跟随法的基础上通过对各障碍物引入威胁系数而改进A*算法，在A*最短路径的基础上考虑不同障碍的安全威胁，提高集群的生存率。在利用改进A*算法完成领航无人机全局路径规划后，采用Hermite多项式完成了全局路径的参数化表示。Hermite多项式在路径点多阶连续的特性，可以降低对无人机动力系统的冲击。最后，通过带有动态避障功能的编队协同控制器，实现无人机编队队形的协同控制。

1 问题描述

1.1 无人机运动模型

无人机主要包括多旋翼与固定翼两类，两者的运动学模型并不完全一致。为了使异构无人机也能进行组合并完成协同编队任务，需将无人机统一视作二阶积分系统[12]

(1)

式中，xi,vi∈Rm为无人机的状态量，ui为控制输入量，i=1,2,…,k为积分系统数量。考虑水平面的运动，假设无人机作匀速运动，其运动学模型与运动约束为

(2)

式中，(x,y)为无人机在NED北东地地理坐标系下的位置，BODY为机体坐标系，v、a和λ分别为无人机速度、加速度和速度角，vmax、amax分别为最大速度和最大加速度。各物理量的示意图如图1所示。

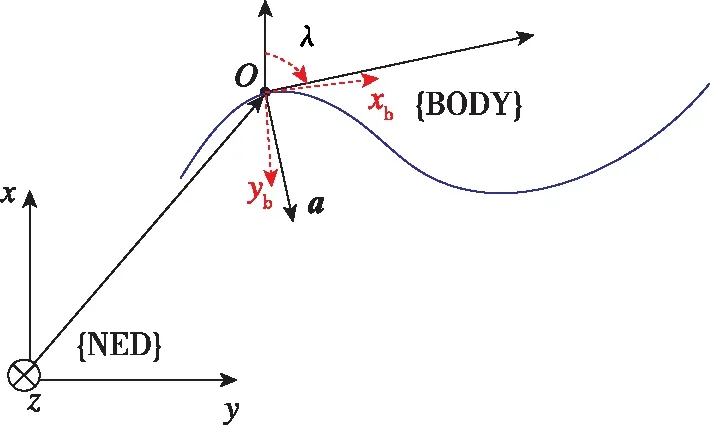
图1 无人机运动模型示意图Fig.1 UAV motion model diagram

1.2 通信拓扑结构

使用图论中的有向图来描述各无人机之间的通信拓扑结构。领航无人机负责全局路径的规划，将各跟随无人机的路径参数进行全局统一分配。其与跟随无人机之间为双向通信，各跟随无人机之间通过互联进行状态信息的同步。无人机的通信拓扑结构如图2所示。

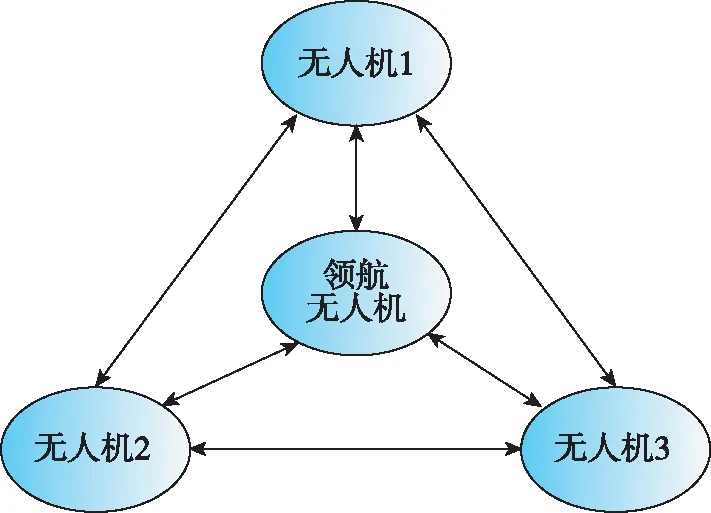
图2 无人机通信拓扑结构Fig.2 Communication topology between UAV

根据图论知识[13]，上述通信拓扑结构可用有向图G=(V,E,A)表示。其由顶点集合V={v1,v2,…,vn}、边集合E和邻接矩阵A=[aij]∈Rn×n组成。若任意∀i,j=1,2,…,n,i≠j，顶点i可直接到达顶点j，则该边存在于边集合E中，可记为(vi,vj)∈E。此时，邻接矩阵A中的元素aij=1。否则aij=0，且记作aii=0，即有

(3)

2 全局航迹路径规划

2.1 改进A*算法

为了最小化任务时间与能量消耗，对无人机进行预先的全局航迹路径规划是必要的。航迹路径规划算法的目标是基于预先给定的地图生成一条最小代价的路径。考虑计算的时间与空间代价，利用启发式搜索的A*算法可以获得理论上的时间最优。其代价函数如下

f(n)=g(n)+h(n)

(4)

式中，n代表当前搜索过程中的节点，g(n)为沿着规划路径从起点到节点n的耗费值，h(n)为从节点n到目标点的耗费估算。g(n)由已产生的路径确定，h(n)的选取会直接影响路径的规划。通常使用曼哈顿距离作为h(n)的估计，如公式(6)所示

(5)

式中，x、y和xd、yd分别是当前节点坐标与目标节点坐标。由于曼哈顿距离只考虑了当前节点与目标节点的预测距离，搜索目标为最短路径，考虑各障碍对集群任务的威胁不同，需引入障碍威胁系数。这里选用了新的预测函数

h′(n)=

(6)

式中，ma为权重系数，wi(x,y)为第i个障碍在(x,y)处的威胁系数，ri_max是在路径搜索过程中无人机与第i个障碍中心距离的预设最大值，ri是无人机与第i个障碍的中心距离，k为障碍个数。

路径点搜索的流程如下：

(1)路径初始化

将搜索区域网格化，将起点A周围可通过的节点加入到open列表，将A加入到close列表。其中，open列表存储了待搜索的节点，close列表存储了最小代价点以及不再需要搜索的节点。

(2)搜索节点

从A点开始，向周围8个方向对存在于open列表中的节点进行搜索。依据上述代价函数计算各节点的代价值，选取其中的最小代价值节点，将其从open列表中移除，并将其加入到close列表。设置当前节点为最小代价点的父节点，然后从该子节点开始进行搜索。重新添加子节点的周围节点并将其添加到open列表，如果新的待加入节点已经在子节点的open列表中，则计算新的代价值。若代价更小则更新该值，并更新父节点为当前节点，否则保持。

(3)终止判断

循环上述步骤(2)直至目标节点被加入到close列表时关闭循环。在close列表中，从目标节点开始，将各节点的父节点根据顺序连接起来直至起点，即为规划的路径。若开启列表为空后还未找到目标节点，则路径搜索失败，如图3所示。

图3 A*算法搜索流程图Fig.3 A* algorithm search flow chart

引入威胁系数后，搜索的方向将变为路径代价与威胁代价和最小的方向，两者的优先级可以根据实际任务通过权重系数进行调整。改进前后的A*路径搜索对比如图4所示。3个蓝色网格为障碍，绿色和红色网格分别为起点和终点。设每个网格的长度为10，对角线长度为14，则在ma=0.5、wi(x,y)=1、ri_max=70时，改进前和改进后的搜索网格数分别为34和52。两条路径的长度均为68，与障碍中心的累计距离分别为120和128。改进之后，A*搜索路径的次数虽然增大了，但路径长度均为68，且降低了路径平均威胁。

2.2 离散航迹路径优化与编队队形表示

由上述步骤生成的路径为全局曲线路径。考虑降低数据链的通信需求，本文采用离散路径结合曲线拟合的方式对该路径进行参数化表示。领航无人机的规划路径Ω是网格化后的离散路径点的集合，从当前位置沿路径Ω在到达目标点之前截取一段长度为L的路径，采用Hermite多项式对路径Ω进行参数化表示[14]。

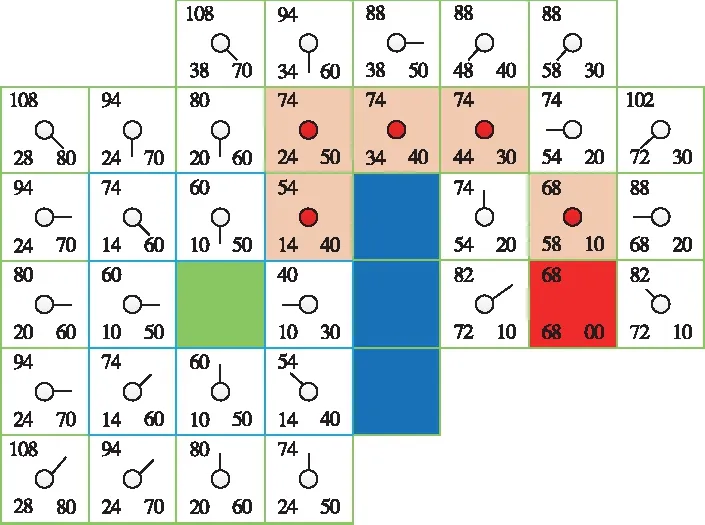
(a)传统A*算法

路径Ω的参数化信息包含m+1个路径点Pi=(xi,yi)，以及路径点上对应的导数qi，i=0,2,…,m。选取拟合曲线在离散路径点处的切线与离散路径点前后折线的角平分线垂直，则起始点与路径折线的斜率相同，可由此计算各路径点的导数qi

(7)

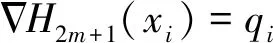
(8)

选取Hermite多项式插值基函数αi(xk)、βi(xk)，并满足

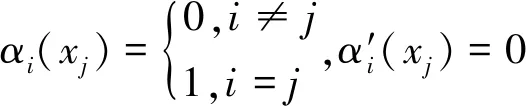
(9)

利用插值基函数表示Hermite多项式H2m+1(x)=H(x)

(10)

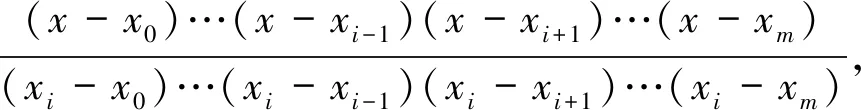
(11)

式中，k1,k2，k3,k4为引入的临时中间变量。根据式(8)～式(11)，可得到该路径的分段3次Hermite多项式

(12)

式中，x∈[xi,xi+1]，(i=0,1,…,m-1)。由式(12)可得到利用Hermite多项式进行参数化后的领航无人机路径，但该路径有可能重新进入障碍物影响范围，因此需要重新优化路径。可采用如下的局部重新规划方案：在发生碰撞的路径的下一路径点B、新增点B的前后两条原始路径点的连线中点D和E重新生成新的曲线。重复该步骤，直至曲线满足运动学约束与避碰要求。优化后的示意图如图5所示。

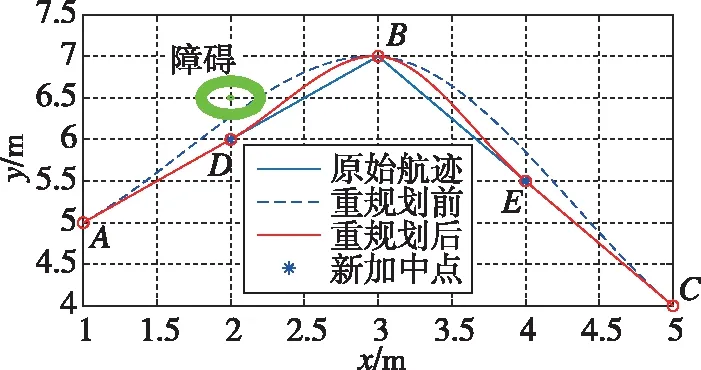
图5 重新规划路径优化示意图Fig.5 Re-planning path optimization diagram

考虑跟随无人机的编队路径Ωi，由领航无人机为编队中的所有跟随无人机分配队形位置。为了直观描述编队队形，首先以领航无人机的位置为原点，建立Serret-Frenet(SF)坐标系[15]。其中，速度切线方向为xsf轴，法线方向为ysf轴。在SF坐标系下，无人机i到无人机j的期望编队坐标向量为dij=(xoff_ij,yoff_ij,zoff_ij)，i,j=0,1,2,…,n，n为跟随无人机数量，领航无人机的编号为0。第i架跟随无人机的路径Ωi生成参考领航无人机，在将相对于领航无人机的编队坐标向量d0i旋转到NED北东地地理坐标系下后，将其添加到领航无人机的离散路径点上，再用Hermite多项式进行表示

Ωi=Ω+R(-λ)d0i(i=1,2,…,n)

(13)

式中，λ为1.1节所述的速度角，R(-λ)为绕NED北东地地理坐标系z轴转动-λ角度的方向余弦矩阵。无人机在SF坐标系下的队形示意图如图6所示。

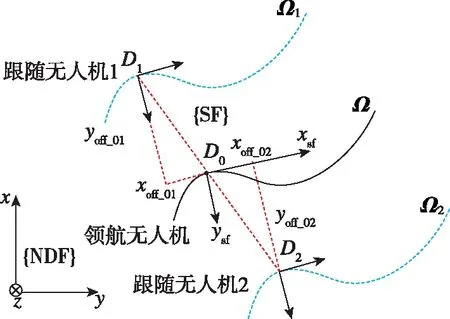
图6 Serret-Frenet 坐标系下的编队队形示意图Fig.6 Swarm formation diagram under Serret-Frenet coordinate

3 编队协同控制器设计

3.1 路径协同控制器设计

无人机编队任务多种多样，常需要在编队飞行过程中进行队形变换以躲避障碍物、切换任务等，或者在到达目标点上空后进行盘旋、环绕，以对目标进行侦察等。随着队形的切换以及时间的推移，如果不加修正，则无法保证无人机按照预期的队形飞行。因此，需根据一致性原理设计路径协同控制器，使编队队形满足

(14)

式中，Di为第i架无人机在SF坐标系下的实际位置。定义无人机i编队队形误差ζei为

(15)

根据上述1.2节的图论知识，可将上式改写为矩阵形式

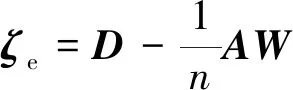
(16)

无人机的运动模型采用了上述1.1节的二阶积分模型。这里，将二阶积分模型具体细化为加速度与速度。为使编队误差趋近于零，可将路径协同控制器分为两部分：单机基于路径跟随完成对上述2.2节规划的路径的跟踪，以及多机路径协调。其中，在路径跟踪中采用上述1.1节的二阶加速度作为控制量，利用L1算法实现路径的稳定跟踪[16]，而路径协调则采用了速度控制量。

由L1算法实现路径跟踪而生成的横向加速度控制量acmd为

(17)

式中，L1为从无人机当前位置到期望路径上参考点的向量，其长度大小为一个预设的定值。η是L1向量到无人机预设期望飞行速度向量v的夹角。考虑到无人机的速度限制，设计在采用L1算法跟踪路径时限制路径跟踪的分速度Vd为

(18)

式中，vmin、vmax和Δv分别是无人机最小、最大飞行速度和路径协调控制器的可调速度，可设计如下的路径协调控制器

Vr=Vd-Δvf(ζe)f(x)=2/(1+e-x)-1
f(x)∈(-1,1)，x∈R

(19)

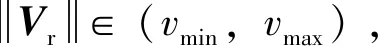
3.2 动态障碍避障控制器设计

考虑跟随无人机与无人机以及无人机与外部之间的动态障碍避障，可采用结合路径预测的人工势场法进行避障。

人工势场法的目的是构造包含斥力与引力的合势能函数，使得无人机在势力引导下改变飞行路径[17]。其中，引力可引导无人机前往目标点，而斥力可使无人机避开障碍物。3.1节已经完成了对目标编队的引导，这里只需考虑斥力的避障。

在构造斥力场函数时，为保证无人机与无人机或无人机与其他障碍之间在距离较近时能够快速分离，以无人机之间的避障为例，无人机i对无人机j的斥力可采用如下的斥力场函数

(20)

式中，b、c是斥力调节常数，Rmin和Rmax分别表示无人机间最小的安全距离和斥力最大作用距离。距离小于安全距离时，无人机将发生碰撞；距离超过Rmax后，斥力将不起作用。由式(20)可得无人机i对无人机j的斥力为

(21)

无人机i所受的合斥力为

(22)

由式(22)可得斥力矩阵为F=[F0,F1,…,Fn]T。考虑在动态障碍情况下的避障轨迹优化。无人机在进入碰撞半径后，动态的障碍运动轨迹与无人机避障后的合成运动轨迹可能仍然存在碰撞的可能，或产生的避障控制量大于无人机运动学限制，因此动态障碍下的轨迹优化过程如下。

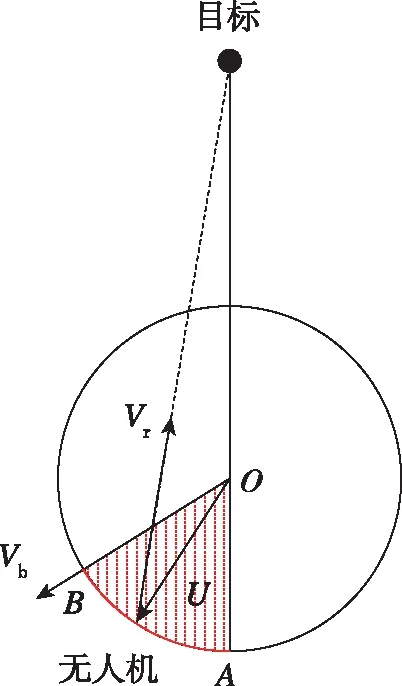
(a)情形1

(23)

式中,U为障碍对无人机的斥力，Vb为障碍运动速度，c1、c2分别为表征两者速度方向的中间矢量。当满足上述条件时，新的斥力Un为

(24)

式中，Vt为障碍圆心O指向目标的单位速度向量。R(90)和R(-90)分别表示绕上述NED地理坐标系z轴转动正负90度方向的方向余弦矩阵。将式(21)的各分斥力按照式(23)和式(24)处理后，再由式(22)可得加入动态避障的新合斥力矩阵Fn。

综上，将上述3.1节所述的路径协同控制器结合动态避障控制器后，可得到最终避开障碍情况下编队协同控制器的速度量输出Vout

(25)

式中，fm为无人机的质量系数。

4 仿真验证

通过三架无人机的典型的协同编队队形保持与避障，对上述方法进行了验证，并给出了仿真结果。

首先，期望的编队路径由第2节所述的路径规划方法生成。将200m×200m的区域划分为80m×80m的网格，并随机设置5个固定障碍，生成各障碍的威胁代价色度图。传统A*最短路径与改进A*路径规划方法的对比如图8所示。由图8可知，传统A*方法在没有障碍阻挡的前提下，选择了前往终点的最短直线路径，而本文的改进A*方法在生成的威胁代价地图基础上，考虑了威胁的代价，进而降低了规划路径上的平均威胁。仿真结果对比如表1所示。

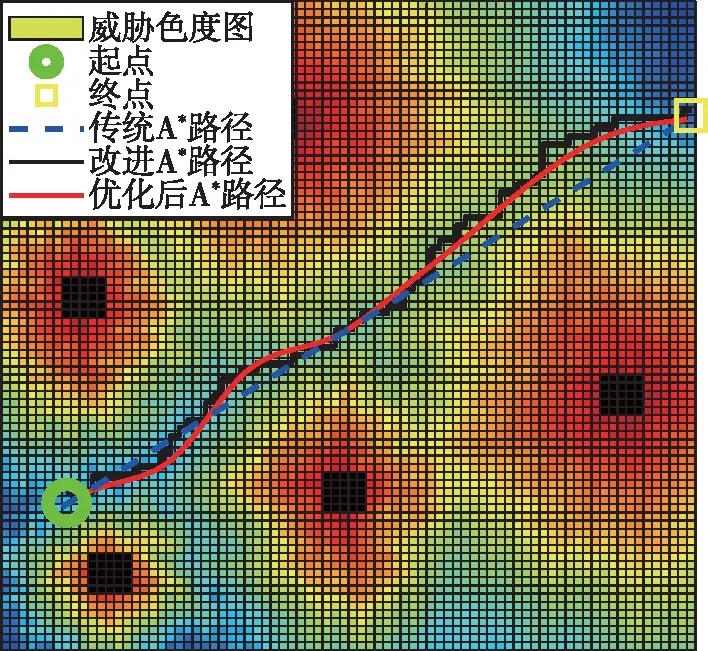
图8 障碍威胁环境下的编队路径规划方法对比Fig.8 Comparison of formation path planning methods under obstacle threat environment

表1 路径规划方法仿真对比Tab.1 Comparison of path planning methods simulation

其次，为无人机设定初始仿真条件。无人机1、2、3的初始位置分别为(10，0)、(20，20)、(0，60)，单位为m，对应的初始速度分别为(5，1)、(2，3)、(4，2)，单位为m/s。其中，2号为领航无人机，1、3号为跟随无人机。静态障碍的起始坐标为(113m，53m)，移动速度为4m/s，移动航向角为45°，障碍影响半径为40m，最小安全半径为25m。无人机的期望速度为5m/s，最大速度为10m/s，最大加速度为5m/s2。跟随无人机按照编队间隔y向各20m的队形，参照领航无人机路径飞行。速度量标准差为0.1m/s，位置量标准差为0.2m。设置采样周期1ms，仿真时间50s。

在考虑动态障碍的前提下，采用本文的改进领航-跟随方法的编队飞行轨迹与编队误差如图9所示。由图9可以看出，各无人机均能在避开动态障碍的情况下按照规划的全局路径飞行。在飞行过程中，无人机从初始位置起逼近队形，编队误差减小并趋近于零；在遇到障碍时，通过改变速度调整队形避障，编队误差增大；穿过障碍后，编队误差再次减小，各无人机开始稳定跟踪期望路径并保持了队形。

图10是传统领航-跟随法与采用路径跟随的改进领航-跟随法的编队误差对比图。图10(a)、图10(b)是两架跟随无人机的编队误差，图10(c)是领航无人机的编队误差。由图10可以看出，领航无人机的编队误差区别不大，但跟随无人机在采用了基于路径跟随的改进领航-跟随协同编队方法后，通过路径参数的预先同步与路径跟随协同，编队误差低于传统的领航-跟随方法。因此，采用本文的基于路径跟随的改进领航-跟随方法，可以实现更高的集群无人机编队精度。

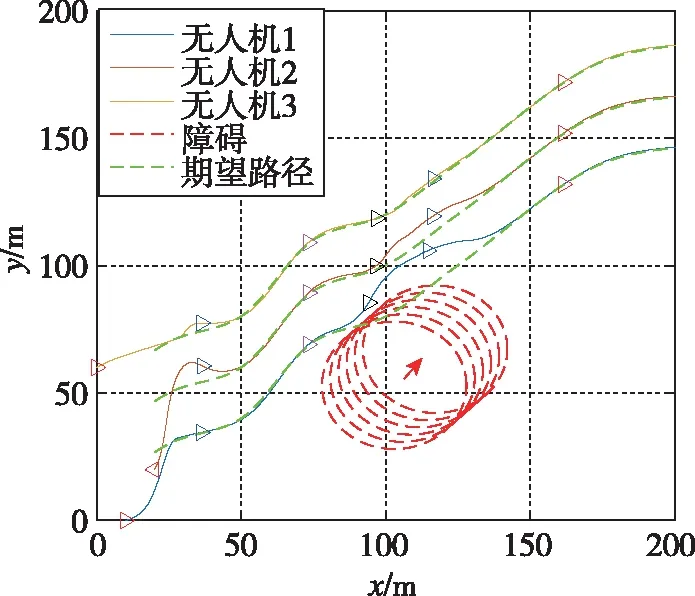
(a)编队飞行队形

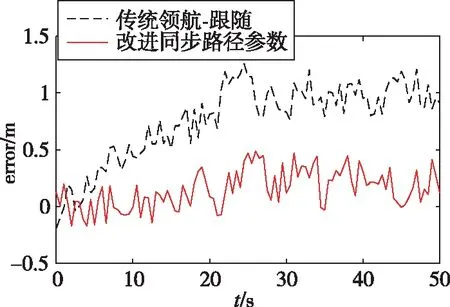
(a)无人机1的编队队形误差

5 结 论

本文研究了领航-跟随法无人机的编队路径最优规划，以及动态障碍环境下路径跟随与协同编队队形保持问题。通过改进A*算法与Hermite多项式，分别完成了全局安全路径最优规划与编队路径参数化表示，并利用一致性原理与改进的人工势场法实现了动态障碍环境下的编队协同控制。仿真结果表明，与传统的领航-跟随方法相比，本方法可以获得更优的全局路径，以及更高的协同编队精度。此外，本方法采用了路径参数协调同步，可以降低对通信系统的要求，选取的Hermite多项式路径参数可以获得光滑的二阶动力学控制量，使编队的飞行过程更为平稳，因此具有一定的工程应用价值。