基于矩阵分解的个性化轨迹推荐方法

潘 晓 马 昂 闫晓倩 吴 雷

(石家庄铁道大学 河北 石家庄 050043)

0 引 言

随着无人驾驶、智能汽车和车联网等技术的发展，大量的轨迹数据迅速积累[1-5]。同时，伴随社交媒体应用的流行普及，地理位置与文本数据的融合，大量外部信息被嵌入到轨迹中，形成了多属性轨迹，轨迹上的每一个点同时包括位置、时间戳、活动和其他描述性多属性。多属性轨迹数据中包含了反映移动特征、个性化偏好等丰富信息[6]。基于历史多属性轨迹制定出行计划可以为用户提供更加友好和个性化的出行体验[7]。本文从用户历史多属性轨迹中自动学习用户个性化的行为偏好，为用户提供满足行为偏好的路线推荐。

目前已经存在了一些在多属性轨迹上的推荐研究[6-15]。文献[10]通过用户签到数据，提出了一个时间敏感的路径推荐方法，通过构建三维张量进行用户偏好估计得到候选位置点，结合位置点的合适访问时间，以及位置点之间的路程时间，对经典的最短路径算法进行扩展，提出了路线生成算法。文献[8]利用Flickr中的数据，提出一种基于兴趣点(Points of interest,POI)流行度和基于时间的用户兴趣偏好的个性化旅游路线推荐算法PTIR，在给定旅行时间限制、起点和终点的情况下，结合用户兴趣偏好设计最优旅游路线。虽然，文献[8]和文献[10]在推荐时考虑到了时间、空间和地点流行度等因素，但是忽略了多属性轨迹中的文本属性对推荐的影响。

文献[9]结合了用户轨迹数据和社交平台数据，将用户的偏好形式化地表示为关键字集合，设计了一个关键字提取模块对POI相关标签进行分类，以便与查询关键字进行有效匹配。通过路径重建算法构建满足符合用户指定关键字需求的轨迹。借助Skyline概念，向用户推荐在不同POI特征之间均不能被控制(dominate)的轨迹路线。文献[5]提出一种基于短时间体验式路线搜索方法SERS，该方法根据用户给定的查询位置、时间约束以及用户指定的文本类别集合，找到一条地点非重复、包含类别最多、收益最大的访问路线。上述工作虽然考虑到了多属性轨迹中的文本属性，但均没有考虑用户个性化的出行行为习惯。

与上述工作不同，本文无须用户手动设定行为偏好，通过简单地指定起点和终点位置，即可为用户推荐个性化的出行路线。

1 预备知识

1.1 相关定义

用户的兴趣偏好蕴含在用户的活动即多属性轨迹中。多属性轨迹中的每一个位置点的语义都可体现用户在该点进行的活动，如就餐、锻炼和购物等。这些活动以文本标签的形式与位置点关联。定义1给出了多属性轨迹的定义。

定义1多属性轨迹。一条多属性轨迹ti={pi,1,pi,2,…,pi,3},其中活动点pi,j=，代表用户i在timj时刻和vj点进行了活动，活动的文本标记集合用sj表示。

表1列举了6个用户的多属性轨迹，包括位置点、时间以及在位置点上进行的活动(即文本集合)。用户的行为与用户在某一个位置点进行的活动内容有关，更与用户连续进行的活动相关。比如，健身爱好者在工作后喜欢去健身房健身。因此，将用户在多属性轨迹上的两个连续位置定义为用户行为。

表1 多属性轨迹

定义2用户行为。给定用户轨迹集合,一个用户行为bk表示用户在时间(timi,timj)内连续在(vi,vj)两位置点进行了活动si和sj，形式化地表示为：

bk=<(vi,vj),(timi,timj),si∪sj>

(1)

根据定义2，可以从表1中的6条轨迹中抽取10个用户行为，具体信息如表2所示。为防止时间粒度过细造成的数据稀疏问题，将时间进行了分段。例如，以24小时为例，每2个小时为1段，共12段。

表2 用户行为

将用户行为以有向图的形式组织起来，图中的点即带有时间和文本的空间点，边即一个行为。定义3给出了具体定义。

定义3行为图。行为图G是一个有向图，G=，V是由所有用户的轨迹中的所有活动点组成的集合，其中每一个活动点p∈V包含空间位置、时间和文本集合三个部分。E是由轨迹中连续两个点组成的边集合，即ei,j=，其中vi,vj∈V。由定义2可知，图G中的每一条边即用户的一个行为b。图G上的每条边都被赋予一个权重，表示某用户发生此行为的概率。因此，不同的用户在图G的同一条边上具有不同的权值。

定义4是轨迹推荐问题的形式化定义。

定义4轨迹推荐。给定用户的起点v0和终点vd，轨迹推荐方法会为用户u返回一条轨迹t=(v0,v1,…，vd)使得概率p(t|u)的值最大，即：

p(t|u)=p(v0,v1,…,vd|u)=

p(v0,v1,…,vd,u)/p(u)

(2)

假设用户的行为相互独立，轨迹概率p(t|u)的值最大，即为p(u,b1)×p(u,b2)×…×p(u,bn)最大。设L=1/p(u,b1)×p(u,b2)×…×p(u,bn),则求解p(t|u)的值最大问题转化为了求解L最小值问题，对L进行取对数变换，计算式表示为:

(3)

根据式(3)可知，计算轨迹概率最大问题，可以转换成寻找若干个用户行为，使得用户行为概率倒数之和最小问题。结合定义3中的行为图，每一个行为发生的概率即行为边的权重，则求解轨迹概率最大问题可转变成基于图的最短路径问题。

1.2 研究框架

本文的研究框架大体可分为2部分，具体如图1所示。

图1 研究框架

首先，在对用户轨迹数据进行了异常点预处理后，利用多属性轨迹构建用户行为图和用户行为概率矩阵。通过分析真实数据发现，用户行为数据非常稀疏，存在大量未知的用户行为概率值。为了解决稀疏问题，本文提出基于矩阵分解的用户行为概率学习方法，对用户行为概率进行估计。

其次，使用贝叶斯方法对轨迹概率进行计算，如式(2)所示。结合用户给定的起点和终点，基于用户行为概率采用双向Dijkstra算法[12]——一种对传统Dijkstra算法在时间效率进行的改进算法，轨迹推荐将返回使概率最大的轨迹作为参考。

2 基于矩阵分解的用户行为概率学习

矩阵分解是协同过滤中一种有效并且常见的方法，旨在通过构建用户项目矩阵来预测用户的偏好。本节首先构建用户行为频数矩阵UB，然后利用矩阵分解方法对用户的行为频数进行估计，进而得到用户行为概率。

2.1 用户行为频数估计

采用矩阵分解法对用户行为频数进行填充。假设用户和用户的行为是受一定因素影响的，即pui、qbj分别代表影响用户和用户行为的潜在因素向量，如式(4)和式(5)所示，其中k为因素的个数。矩阵分解不探究这些因素具体是什么，而是通过这些因素得到受这些因素影响的用户ui产生行为bj的频数。

pui=(fui1,fui2,…,fuik)

(4)

qbj=(fbj1,fbj2,…,fbjk)

(5)

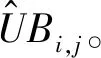
(6)

式中：S是已知频数的用户ui和行为bi的集合；UBi,j是用户ui发生行为bi的频数；因素向量pui和qbj的乘积代表估计值；常数η为正规化参数，防止发生过拟合。

2.2 计算用户行为概率

用户的行为概率描述了用户的选择执行该行为的可能性，可通过下式计算：

(7)

式中：a为平滑参数。

通过式(7)，用户行为频数矩阵转变为用户行为概率矩阵Pro={pi,j}，即已获得行为图中的边权值。给定用户起点v0和终点vd，轨迹查询推荐方法将利用双向Dijkstra算法为用户u返回概率最大的轨迹。

3 实验与结果分析

3.1 实验设计

从Foursquare数据集的LA和NYC中，将用户签到时刻以升序排序得到每一个用户的签到轨迹,轨迹上每一个点均包含签到时间、签到位置、签到POI的类别集合信息。从中随机选取了2 000条轨迹，剔除签到频数低于30、签到用户数低于10的签到冷点，并对其利用Geohash方法进行了网格划分。

本文所有的推荐模型和算法均用Java语言实现，运行于2.7 GHz处理器、16 GB内存的Windows 10计算机上。实验选择了基于马尔可夫的推荐方法[15](简称为Markov)、基于多因素融合的推荐方法[14](简称为UBPMF)进行对比验证。

本文采用F-Measure方法，计算精确度P和召回率R的加权调和平均，具体计算如下：

(8)

(9)

(10)

式中:当α取1时，F-Measure为F1-Measure。

3.2 结果分析

实验评价可以分为两部分：推荐结果准确性评价和查询效率评价。其中，由于查询直接采用的是双向Dijkstra算法，查询效率方面不做特别的评价。本节将具体介绍推荐结果准确性的评价。

(1) 用户平均好友个数对推荐结果的影响。用户平均好友个数不同时各方法推荐结果的变化如图2所示。由于马尔可夫方法并没有考虑用户的好友关系，所以本文仅评价了UBPMD和UBPMF。图中横轴代表用户平均好友个数，纵轴为推荐评价标准F值。可以看出，UBPMF方法得到的平均F值略低于UBPMD方法，但这两种方法下平均F值随好友个数的变化趋势大体相同。当用户好友个数为0时，推荐的准确度仅依靠用户自身的历史轨迹数据，平均F值低于0.40。用户好友数量介于0至22时，随着用户数量的增加，平均F值处于波动状态，总体呈现下降趋势。这是由于当用户数量较少时，可能无法体现出该用户的行为偏好，甚至会对用户偏好产生消极影响。在用户好友个数为23时，平均F值处于顶峰。用户好友数量介于22～65时，随着好友个数的增加，平均F值总体呈现上升趋势。用户好友数量大于65后，平均F值开始下降。通过上述实验表明，过高和过低的好友数量会对推荐结果的准确度产生一定的影响，用户好友数量介于50～60时，推荐准确度较高。

图2 用户好友个数与F值的关系

(2) 不同轨迹长度对推荐结果的影响。用户轨迹长度不同时对各方法推荐结果的影响变化如图3所示。图中横轴代表用户轨迹长度，纵轴为推荐评价标准F值。可以看出，随着轨迹长度的增加，推荐结果的平均F值呈现下降趋势。轨迹长度过长，推荐结果的准确度越低。当轨迹长度介于4～12 km时，推荐结果的准确度较高。结果表明，在进行用户行为偏好学习时，用户轨迹不宜过长，这一点比较符合人们直观认知，轨迹过长说明用户签到次数过多或者经历的时间周期较长。例如，一周内的轨迹与半月内的轨迹相比，一周内的轨迹更具有一定的规律性，轨迹过长无法准确反映出用户的行为习惯。

图3 轨迹长度与F值的关系

(3) 不同数据集下各方法的推荐效果评价。在LA和NYC数据集上，分别评价和比较基于矩阵的用户行为概率学习方法CFPTR、基于多因素的用户行为概率学习方法MFPTR以及基于马尔可夫模型的推荐方法MTR的推荐效果。

参数设定：基于矩阵分解的潜在因子的数量设定为4，正则化参数π设定为0.01，平滑参数a设定为0.01。基于多因素概率密度函数方法中，基于空间因素中的灵敏度参数α设定为0.1。

图4展示了在LA和NYC数据集上根据三种方法得到的F-Measure值。以LA为例，基于矩阵分解的用户行为学习的轨迹推荐方法和基于多因素概率密度函数的用户行为概率学习的轨迹推荐方法在F值方面都优于基于马尔可夫的轨迹推荐算法。在这三种方法中，基于矩阵分解的用户行为概率学习方法的F值最高为0.46，基于多因素概率密度估计的方法F值为0.41，基于马尔可夫的方法为0.40。

图4 轨迹推荐结果评价

结果表明，与基于马尔可夫的轨迹推荐方法相比，用户更喜欢具有最大行为概率的路线。实验表明用户在选择路线或者出行方案时不仅考虑距离因素，而且还综合考虑了许多因素，例如：时间、文本和社交关系等。尽管如此，基于矩阵分解的用户行为学习的轨迹推荐方法取得了比基于多因素概率密度函数的用户行为概率学习的轨迹推荐方法更好的结果，上述因素在轨迹推荐中是作为整体对用户的行为产生影响的，这在路线推荐中起着非常重要的作用。

4 结 语

本文针对现有大多数轨迹推荐工作仅关注时空特征，无法用户个性化行为习惯的问题，在多属性轨迹上同时考虑了用户前后联系活动，通过矩阵分解自学习用户行为习惯，并将用户推荐个性化的轨迹路线转换为在行为图上寻找最短路径的问题。经过一系列实验，基于用户行为学习的矩阵分解的轨迹推荐方法展现了较好的效果。在未来的工作中，将致力于基于多源数据融合的轨迹推荐，可以使用多源数据来进一步提高推荐质量。