计及风电与电动汽车随机性的两阶段机组组合研究

王若谷，陈果，王秀丽，钱涛，高欣

(1.国网陕西省电力公司电力科学研究院，西安市 710100；2.西安交通大学电气工程学院，西安市 710049)

0 引 言

当今时代，风电等新能源和电动汽车在给国家能源产业和环境问题带来巨大机遇的同时，也给电力系统运行和调度带来了巨大的挑战[1-2]。并且随着风电和电动汽车并网规模的增大，这种影响也将与日俱增。风电出力的随机性和间歇性以及电动汽车充电负荷的不确定性让传统的电力系统调度方案不再适用，如何在考虑到风电与电动汽车影响的基础上，保证电力系统的稳定可靠运行，尽量减少系统的运行成本已经成为当下的研究热点。

近年来，国内外的研究学者对风电出力不确定性建模方法进行了广泛的研究[3-6]。其中，场景分析是最为有效且简便的方法之一。文献[7-8]基于场景分析建立了随机调度模型，实现了对风电不确定性的定量分析。在这种描述不确定性的方法中，场景的生成方式至关重要。本文采用生成对抗网络(generative adversarial network, GAN)方法来生成场景，通过生成模型(generator)和判别模型(discriminator)的互相博弈学习使生成场景与真实数据具有相同的分布。相对于基于采样的场景生成方法，GAN方法的优势是其完全是数据驱动的，生成场景的质量由所观测到的历史数据决定[9-10]。

关于电动汽车建模方法的研究也有很多[10-15]，一般都会在电动汽车的模型中考虑电动汽车的充放电功率约束以及能量守恒约束。很多研究都是基于单个电动汽车来建立模型，并添加上述约束条件。针对电动汽车个体建模的方式实现起来较为简便，但是随着电动汽车规模的增加，约束条件的个数也会迅速增加，使问题的规模增大到不能接受的程度。在有些研究中[14]，为了克服这种缺点，会对电动汽车分组并假设同一组中的电动汽车(EV fleet)有相同的参数和特点，这样尽管减小了问题的规模，但却与现实情况不太相符。在文献[11,15]中，电动汽车被考虑为通过一个充电聚集商(EV aggregator)来与电力系统进行功率交换。在这种模式下，电动汽车不再作为个体来与电力系统交互，同属一个充电聚集商的电动汽车也不必被强制设定为具有相同的参数，有效地解决了以上问题，但是这些研究在考虑电动汽车的基础上，并未讨论或者仅仅只是简单地考虑了风电不确定性对结果的影响，并未深入讨论风电不确定性的建模以及其与电动汽车随机性的耦合关系。

在未来，风电和电动汽车的规模都将显著增加，其给电力系统带来的巨大挑战不容小视。然而，充分并且同时考虑到两者不确定性的研究尚不成熟。因此，本文旨在采用合适的方法对风电与电动汽车进行不确定性建模，并将两者结合起来考虑，探究两者对电力系统可能带来的影响。

针对风电和电动汽车的不确定性，本文建立基于多场景分析并考虑EV充电聚集商的两阶段随机机组组合模型。对于风电，主要通过场景分析和分阶段建模来定量分析其不确定性。对于电动汽车来说，则将其分为不可调度和可调度两类来分别建模。对于不可调度的电动汽车，本文旨在得到其典型的负荷曲线，并将其直接视为系统负荷的一部分，而不考虑其不确定性；对于可调度的电动汽车则建立了EV充电聚集商模型，并通过抽样对每个充电聚集商管辖区内的电动汽车行为进行模拟，以此来体现其不确定性。本文采用混合整数线性规划(mixed integer linear programming，MILP)的方法进行求解，并通过IEEE 54机118节点系统的分析计算验证所提方法的有效性。

1 风电场景的生成和电动汽车的典型负荷曲线与随机模拟

本文基于场景分析来描述风电的不确定性，并通过随机模拟来描述电动汽车的不确定性。在建立完整的随机机组组合模型之前，先对场景生成的方式和电动汽车进行随机模拟的方法予以交代。

1.1 风电场景的生成

本文通过GAN来实现场景的生成。生成模型和判别模型都采用4层的神经网络实现。在初始化神经网络参数后，通过迭代训练神经网络，在每次迭代中，先固定生成模型的参数，训练判别模型，使其能最大程度上分辨真实风电数据和由生成模型生成的场景。再固定判别模型的参数，训练生成模型，使其生成的场景在判别模型中的得分尽量接近真实数据。经过多次迭代后，GAN就能根据给定的历史风电数据生成所需的风电场景。本文使用GAN生成风电场景的框架如图1所示。

在迭代训练过程中，针对损失函数使用梯度下降法来进行网络权值的更新。生成模型和判别模型的损失函数为：

(1)

(2)

(3)

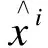
1.2 不可调度电动汽车的典型负荷曲线

针对一般的电动汽车负荷曲线，本文利用k均值聚类的方法来获得电动汽车的几类典型负荷曲线。具体来说，将每一个电动汽车的负荷曲线视为用于聚类分析的一个多维数据点(在进行聚类分析时须对每个数据点进行归一化处理)，k均值聚类算法旨在通过迭代从所有的数据点中挑选出k个聚类中心[16]，这k个聚类中心就可以近似代表不可调度电动汽车的几类典型负荷曲线。

在实际计算过程中，点与点之间的距离采用传统的欧几里得距离，即：

(4)

每次迭代后新聚类的中心通过计算新聚类中各个数据点的均值得到。

为简单计，本文将不可调度电动汽车直接视为确定性电力负荷的一部分，当然，其具体的变化趋势和大小要考虑不可调度电动汽车的典型负荷曲线以及规模等因素。

1.3 可调度电动汽车的随机模拟

本文采用EV充电聚集商的模型来对大规模电动汽车进行描述。在此假设每个电动汽车只受一个EV充电聚集商管辖，并且电动汽车与电力系统之间可以进行双向的电能输送，即电动汽车受到汽车-电网(vehicle-to-grid, V2G)技术的支持[17-18]。并且假设EV充电聚集商的管辖区内有足够多的充电设备，从而每辆电动汽车可以在行程结束后立刻接上充电设备。

根据日常生活经验，假设电动汽车驾驶者的出行需求和行车习惯不会改变。基于这个假设，本文通过电动汽车的相关统计数据得到其相关概率分布信息，然后通过蒙特卡洛模拟方法就可以对辖区内电动汽车的出行规律进行随机模拟。

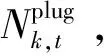
(5)

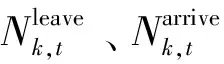
(6)

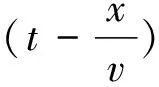
在对充电聚集商管辖区内的电动汽车数量动态变化进行模拟后，可以进一步计算得出充电聚集商的相应属性参数：

(7)

(8)

与电动汽车数量动态变化不同的是，其能量的动态变化不仅与电动汽车的出行规律有关，也与充电聚集商或者说电动汽车的实际充放电过程有关。

(9)

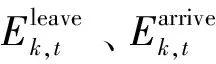
假设当EV离开充电站时，其电池的存储能量需要达到某一特定的水平kh，由此可以得到：

(10)

(11)

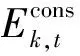
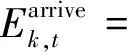
(12)

利用式(5)—(12)就可以实现对可调度电动汽车行为的随机模拟，并得到EV充电聚集商的相应参数。

2 考虑EV充电聚集商的两阶段随机机组组合模型

该模型是一个两阶段的随机调度模型，在第一阶段决策常规机组的启停状态和预留备用量，目的在于求得约束条件下最优的机组组合方式，而第二阶段考虑了应对各场景时运行成本的期望值，并评估在第一阶段中确定的机组组合方式的可行性。本文采用MILP算法并利用CPLEX来对问题进行求解，因此，对两阶段的约束条件都会进行线性化处理[19]。具体模型如下详述。

2.1 目标函数

模型的决策目标是机组启停成本，机组预留备用成本，各个场景下机组燃料成本以及弃风、切负荷的损失费用的期望值之和达到最小。

(13)

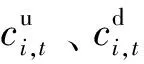
2.2 第一阶段约束条件

1)功率平衡约束。

(14)

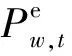
2)机组出力及备用约束。

Pi,t+ri,t≤Pmax,ivi,t

(15)

Pi,t-ri,t≥Pmin,ivi,t

(16)

(17)

式中：vi,t表示机组的启停状态，是一个0-1变量；Pmax,i、Pmin,i分别表示第i台机组的最大、最小输出功率；RUi、RDi分别为机组的上爬坡能力和下爬坡能力。本文假设机组的上备用量与下备用量相同。式(17)对机组的备用量进行了约束[20]。

3)机组启停成本约束。

为了对机组启动成本约束进行线性化处理，需要先对启动成本曲线进行离散化处理，用一个阶梯状的曲线来近似代替原本的启动成本曲线。

(18)

(19)

(20)

(21)

4)最小开停机时间约束。

最小开机时间约束为：

(22)

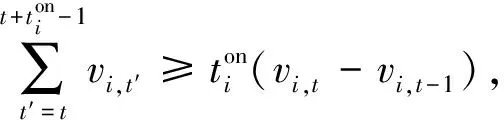
(23)

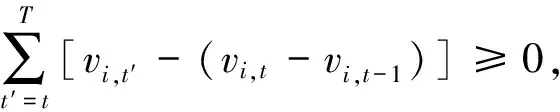
(24)

最小停机时间约束为：

(25)

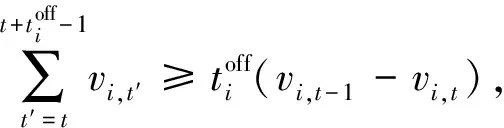
(26)

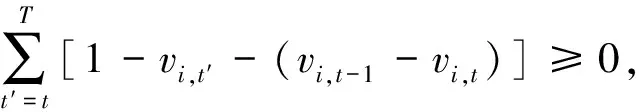
(27)

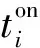
5)电动汽车相关约束。

(28)

(29)

(30)

(31)

式中：kl为由于技术层面原因，电动汽车所能存储电能的最低水平。式(28)、(29)为最大充放电功率约束，对EV充电聚集商的充放电功率大小进行限制。式(30)、(31)分别从充电聚集商的存储容量以及电动汽车的行车需求方面对充电聚集商的能量进行了约束。

6)网络安全约束。

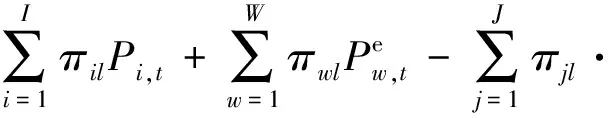
(32)

式中：Fl为线路l的传输功率极限；πil为从机组i到线路l的功率分布因子；πwl为从风电站w到线路l的功率分布因子；πjl、πkl分别为从常规负荷j、EV充电聚集商k到线路l相应的功率分布因子；I、W、J、K分别为常规机组、风电站、电力负荷结点和EV充电聚集商的数量。

2.3 第二阶段约束条件

1)功率平衡约束。

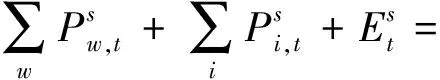
(33)

(34)

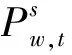
式(33)实际上表示的是各个场景下的功率平衡条件，并计及了极端场景中可能出现的弃风和失负荷现象。

2)机组出力与备用约束。

(35)

(36)

(37)

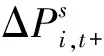
3)机组燃料成本约束。

与机组启动成本约束的处理方法类似，对机组的燃料成本特性曲线进行分段线性化。

(38)

式中：gi,n(·)为燃料成本的分段线性函数；NLi为分段数。

4)机组爬坡约束。

本文不考虑爬坡约束对其他约束的影响。

(39)

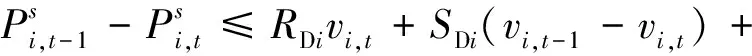
(40)

式中：SUi、SDi分别为机组i的开机爬坡能力和关机滑坡能力。式(39)和式(40)保证了机组出力在相邻时段内的差值在上爬坡能力RUi和下爬坡能力RDi的限制范围内，并且在机组开机爬坡和关机滑坡时爬坡速率受到开机爬坡能力SUi和关机滑坡能力SDi的限制。

5)电动汽车相关约束。

考虑与第一阶段相同的约束条件，但此时的约束对应于每个实际场景。

(41)

(42)

(43)

(44)

(45)

式(5)—(45)构成了两阶段随机优化模型，使用YALMIP在Matlab中进行模型搭建，并利用CPELX进行计算求解。具体求解的流程如图2所示。

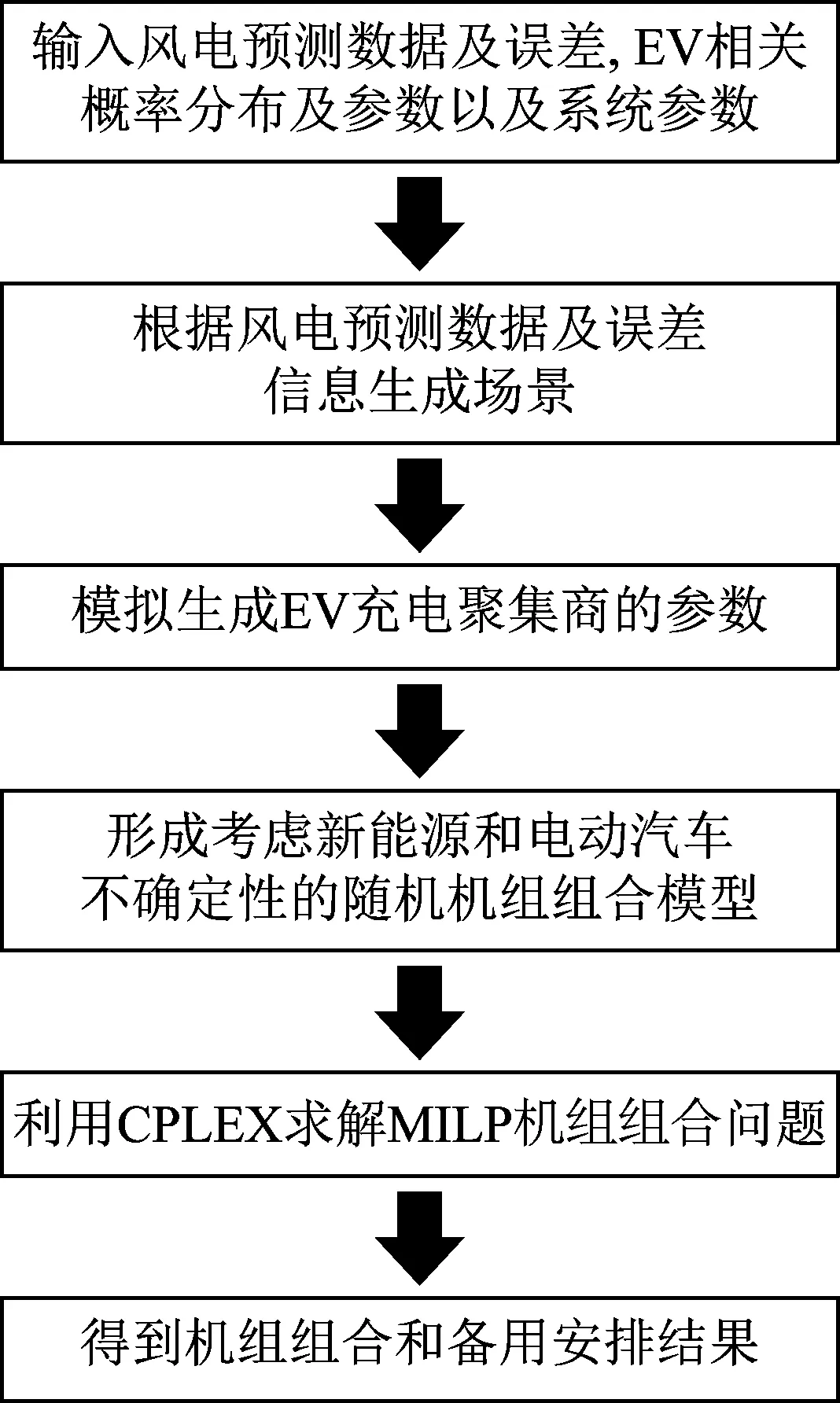
图2 两阶段随机优化模型求解流程Fig.2 Flow chart of modeling and solving

3 算例分析

3.1 算例数据

本文通过标准IEEE 118母线54机系统来验证模型的有效性和可靠性。该标准系统属于地区级网络，考虑系统中存在6个风电站以及6个EV充电聚集商。

电动汽车的总量考虑为120 000个，使其最大的充电功率达到系统最大负荷的10%。对可调度电动

汽车，假设电动汽车的种类相同，每辆电动汽车存储容量为20 kW·h，最大充放电功率为6.4 kW，每km耗电为0.15 kW·h，充放电效率均为0.8，最低存储电量水平为0.2，能够离站的存储电量水平为0.8。电动汽车的行驶距离和行驶速度都近似认为服从正态分布，其中行驶距离的期望值考虑为50 km，行驶速度的期望值考虑为30 km/h。

问题求解在PC机上进行，CPU为酷睿(core)i7-8700，主频为3.2 GHz，内存(RAM)为8 GB。

3.2 算例分析

1)两阶段随机优化在备用安排上的优势。

在实际电力系统调度中，往往会采用确定性的备用安排策略，也就是根据系统中的不确定性因素，给各发电机组安排一定比例的备用容量[7,15]。这样安排备用的方式缺少可靠性保证，在机组出力变化的时候，很可能会造成输电网络阻塞的情况。为了避免这种情况的发生又可能会使备用容量安排过多，造成资源浪费和运行成本的增加。而在两阶段随机优化模型下的备用计算充分考虑了系统中的随机性因素，能够更加合理地安排备用容量。2种备用安排策略下的机组组合结果如图3所示。

从图3的结果可以看出，两阶段随机优化模型下系统所需的总备用容量和总运行费用更小。事实上，相较于确定性备用安排策略来说，两阶段随机优化模型将备用容量作为决策变量，能在充分考虑风电和电动汽车不确定性的情况下，给出更为经济的决策方案，避免资源浪费，而这种安排的可靠性由约束式(35)—(37)来保证。

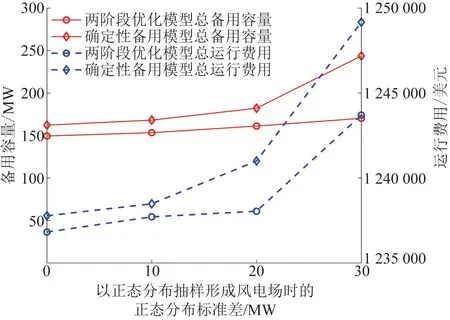
图3 2种备用安排策略的结果比较Fig.3 Comparison of different reserve models

2)电动汽车对风电和电力系统的影响。

为研究不可调度和可调度电动汽车对电力系统的影响，以及电动汽车与风电之间的相互影响，本文设计了3种算例场景：

算例1：系统中不含电动汽车；

算例2：系统中只含有可调度的电动汽车(该电动汽车支持V2G技术)；

算例3：在算例2的基础上额外考虑不可调度的电动汽车。

在计算中，假设可调度电动汽车与不可调度电动汽车的规模相等。3种情况下由两阶段机组组合模型所得到的总备用量、场景平均弃风量、机组运行总成本以及启停机成本如图4所示。

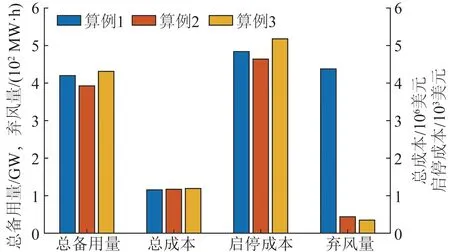
图4 3种算例下的结果比较Fig.4 Comparison of result of 3 cases

(1)可调度电动汽车对电力系统的影响。

从图4中可以看到，算例2相对于算例1，机组的总运行成本有所上升，而机组的启停机成本、备用量有所降低。

机组总运行成本增大主要是因为大规模电动汽车的接入增加了系统的负荷，从而增大了机组的燃料费用。机组启停机成本减少说明可调度电动汽车可以起到一定程度的削峰填谷作用，平滑常规能源的负荷曲线。可调度电动汽车平滑负荷曲线的效果(蓝线是平滑后的结果)如图5所示。

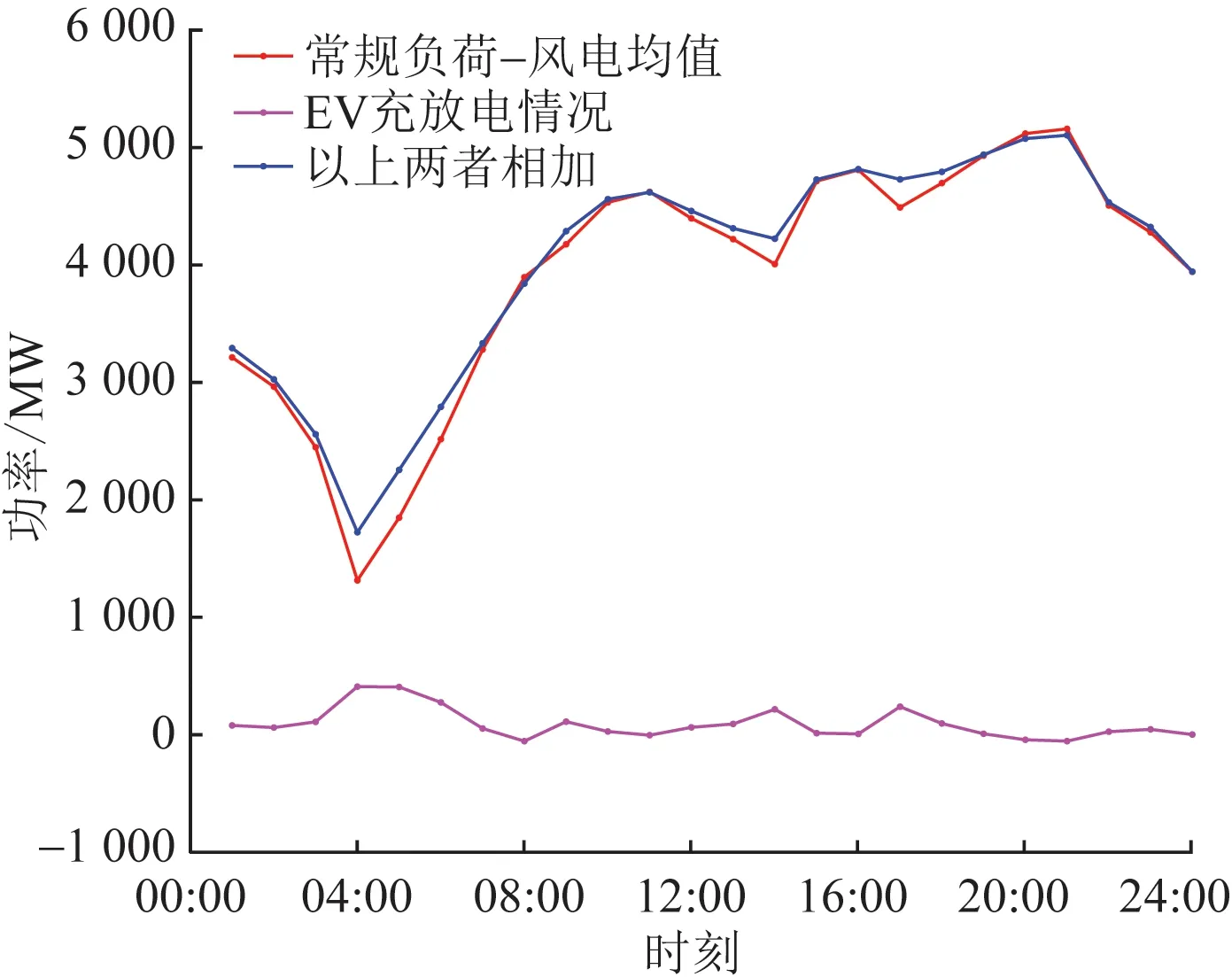
图5 常规负荷与电动汽车充电情况Fig.5 Curve of conventional load and EV charging power

备用量的减少是因为电动汽车的可调度性，或者说是灵活性，可以在风能不确定性较大的情况下，通过充电、暂停充电、甚至放电等方式为电力系统提供临时备用。电动汽车这样的调度灵活性相当于为电力系统提供了一部分的等效备用量。

为了进一步验证可调度电动汽车减少系统备用量的可能性，在算例2的基础上减少或者增加可调度电动汽车的规模，并观察电力系统的预留备用量，结果如图6所示。从图6中可以看到，随着电动汽车规模的增大(每个充电聚集商管辖的电动汽车数量相同)，电力系统需要的预留备用量相应减少。

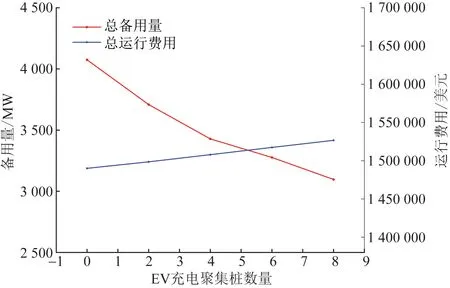
图6 可调度电动汽车规模的影响Fig.6 Influence of the quantity of EVs

(2)可调度电动汽车对风电的影响。

从图4中可以看到，算例2相对于算例1，场景的平均弃风量大大降低。事实上，各个场景出现弃风的情况一般发生在常规负荷低谷期(如图5中的04:00)此时也正好处于风电出力的高峰期，为了维持系统功率平衡便会出现弃风。而可调度电动汽车可以通过在该时段增大充电功率来减少对应的弃风量，具体情况如图5所示。由此可以说明可调度电动汽车有利于系统对于风电的消纳。

(3)不可调度电动汽车对电力系统的影响。

从图4中还可以看到，算例3相对于算例2来说，总运行成本和启停机成本都有所增加，而备用量也有所增加。算例3相对于算例2来说，加入了不可调度的电动汽车，总运行成本的增加同样是由于电动汽车的接入增加了系统的负荷，从而增大了机组的燃料费用。由聚类分析得到的不可调度电动汽车的典型负荷曲线如图7所示。从图7可以看到，不可调度电动汽车的用电高峰和一般常规负荷的高峰重合严重，这增大了常规负荷的峰谷差，从而增加了系统调度的难度并相应增加了机组的启停机成本。

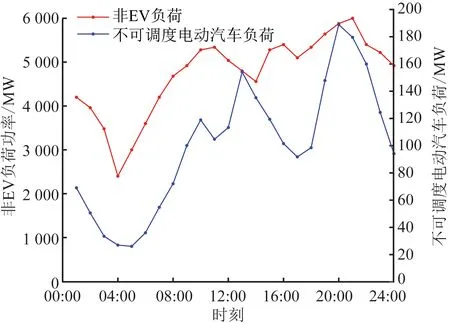
图7 常规负荷与不可调度电动汽车典型负荷曲线对比Fig.7 Curve of conventional load and demand of non-schedulable EVs

4 结 论

本文在充分考虑高比例风电出力和电动汽车充电需求不确定性的基础上建立了电网优化调度和备用计算模型。通过GAN生成风电场景来模拟其不确定性，并通过随机模拟建立充电聚集商模型来应对电动汽车的不确定性。通过在第二阶段引入EV充电聚集商模型来实现任一风电场景下风电与电动汽车的配合。最终建立的基于场景分析并考虑EV充电聚集商的两阶段随机机组组合模型同时考虑了系统中风电和电动汽车的随机性并实现了电动汽车、新能源和传统电源的合理配合。两阶段随机优化模型所确定的备用安排策略相较于传统的确定性备用安排策略更加灵活经济，在保证可靠性的基础上有效减少了所需的备用容量。算例分析结果验证了所提模型的有效性，并且表明可调度电动汽车具有降低系统备用和提高系统风电消纳能力的潜力。