基于混合用户均衡理论和充放电管理的快/慢充电站规划
2021-08-11张林垚郑洁云胡志坚倪识远吴桂联翁菖宏陈志陈锦鹏
张林垚,郑洁云,胡志坚,倪识远,吴桂联,翁菖宏,陈志,陈锦鹏
(1.国网福建省电力有限公司经济技术研究院,福州市 350012;2.武汉大学电气与自动化学院,武汉市 430072)
0 引 言
近年来,随着全球环境压力不断增大,人们对绿色生活的意愿不断增强。电动汽车(electric vehicles, EV)作为绿色出行的主要载体,由于其具有环保、节能、零排放的显著优势受到了各国政府组织及汽车制造企业的青睐。然而,电动汽车保有量的大规模增长对电动汽车充电站规划方法提出了新的要求,若规划不当不仅会威胁配电网的安全稳定运行,并将影响交通用户的出行便利性[1]。
目前,国内外学者已经对充电站规划展开了大量研究。文献[2]考虑车流量、服务质量与投资成本因素对风-光-储与充电站进行协同规划研究。文献[3]以最小化投资与运行费用为目标建立市内快速充电设施规划的数学模型。文献[4]考虑净现值和全周期生命成本对充电站开展选址定容工作。然而现有文献大多仅对单一类型的充电站进行规划方法研究。为了适应不同的应用场景,实际应用中存在沿途快充站与目的地慢充站两类主要的充电设备类型,单独规划不利于全面评估电动汽车与配电网的交互行为,是不完整的。
此外,电动汽车充电功率的时空分布模拟与预测是沿途快充站规划的基础性工作。文献[5]假设所有用户出行均选择空间最短路径并利用重力空间互动模型获取快充功率的空间分布,但忽略了交通道路通行能力对于用户路径选择的影响;文献[6]利用马尔可夫和轮盘赌法计算电动汽车出行链从而预测配网各节点的充电需求,该预测方法仅为基于历史数据对未来的一种概率描述,忽略了智慧交通网背景下的EV用户的空间可转移特性,不能充分适应未来信息互联的发展趋势。
对于目的地慢充站,鉴于其受众的长时间停留特性,对该部分车辆进行充放电管理成为可能。文献[7]制定有序充放电策略分两阶段对充电负荷进行填谷、削峰,其忽略了分时电价对于用户行为的影响。文献[8]建立了基于分时电价的有序充电模型,该模型未充分发挥慢充负荷可向电网放电的灵活性并且未将平抑充电负荷波动性这一重要效用考虑进策略中。文献[9]利用改进粒子群算法以充电费用和负荷方差最小为目标制定充放电策略,该方法受制于群体智能算法的求解能力,无法快速获得全局最优解。上述文献从各方面对充放电策略进行设计,但鲜有文献考虑管理策略对充电站规划的影响。
针对现有文献中存在的不足,文章提出计及电动汽车有序充放电策略的充电站规划模型,充分考虑配电网与交通网的交互,对沿途快充和目的地慢充两种充电装置进行完整规划。首先,基于已在交通运输领域得到充分验证的Wardrop用户均衡理论建立含充电汽车和普通汽车的混合均衡模型以表征信息共享背景下的交通网稳态车流;其次,提出一种基于负荷转移矩阵的电动汽车慢充站充放电策略模型,实现用户充放电套利与平抑充电负荷的联合优化;然后,构建以投资费用与运行等效费用的等年值最优为目标的快/慢充站规划模型,并综合采用分段线性化方法、大M法和二阶锥松弛技术对原约束进行处理;最后,采用IEEE 33节点配电网与12节点交通网的耦合算例进行仿真分析,验证本文方法的规划经济性、负荷平抑优越性和良好的两网互动性。
1 混合交通流稳态均衡下的交通网模型
1.1 交通网模型
交通网络可以由重要的交通枢纽节点集合和交通路段集合组成。每个路段都有各自的最大允许通行容量和自由通行时间。此外,网络中还存有很多O-D点对,每个点对由一个起始节点r和一个终端节点s组成,并能够以点需求的形式表征出交通出行特征。故交通网模型具体可表示为:
1)路段累积车流量。
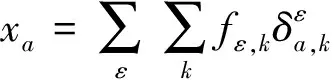
∀ε∈ΛOD,∀k∈Kε,∀a∈Ωroad
(1)
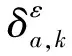
2)交通流量守恒。
(2)
式中:qε为第ε个O-D点对的交通需求量。
3)道路通行时间。

∀a∈Ωroad
(3)
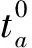
1.2 交通网混合用户均衡模型
沿途快充站主要为路面行驶的EV提供快速充电服务以保证其能够继续正常行驶。基于这一认知,构建交通网的稳态交通流模型关系到快充站的合理配置,是一项基础性工作。
1952年著名学者Wardrop提出用户均衡理论,奠定了交通流分配的基础[10]。在Wardrop用户均衡理论的基础上,本文考虑有充电需求的电动汽车(charging electric vehicles, CV)和普通汽车(normal vehicles, NV)2种出行行为有重大差异的2类车辆,其中需要说明的是本文将无快速充电需求的电动汽车归类为普通汽车进行简化考虑。混合均衡的物理意义定义如下。
定义交通网络的流量分配达到平衡时,在任意O-D 点对间可行路径中,出行者所采用的各条路径上的总出行费用均相等,且不大于未被使用路径上的出行费用。其中,对于CV而言,可行路径为由起点r到终点s且经过沿途快充站的路段组合;对于非电动汽车或者无充电需求的NV而言,其可行路径为由起点r到终点s的任意路径。否则为相应的不可行路径。
混合均衡模型可写为如下数学逻辑表达式:
(4)
(5)
式中:tε,k,ω分别为点对ε间k方案的出行时间;uε,ω为点对ε间的出行平衡时间;∀ω表示任意时刻;上标分别表示变量与CV或NV相关;|·|∨|·|为析取表达,即若干情况的集合。
作为交通混合均衡的纽带,2种类型的交通流量叠加:
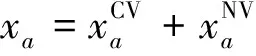
∀a∈Ωroad
(6)
因此,式(3)所示的各道路车辆通行时间应重述为:
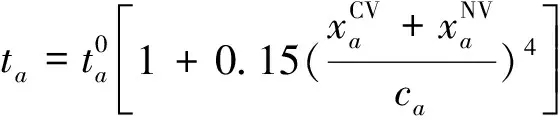
∀a∈Ωroad
(7)
由于CV与NV不同的出行特征,出行等效时间分述如下:
(8)
(9)
2 电动汽车充放电管理模型
目的地慢充的充电适用场景为用户长时间在目的地停留并对电动汽车进行日常性充电。鉴于这种用户特性,通过主动管理手段进行有序充放电调控成为可能。
本文提出一种基于负荷转移矩阵的电动汽车充放电管理模型,具体的慢充管理策略如下。
1)将无意愿参加充放电管理的用户以及停留时间低于调控时间周期t2的用户所对应的电动汽车充电需求视为不可调控的慢充负荷,采用即到即充的恒功率充电模式,且充电时间为t1。
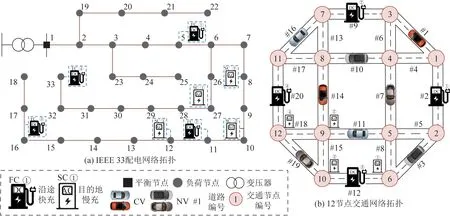
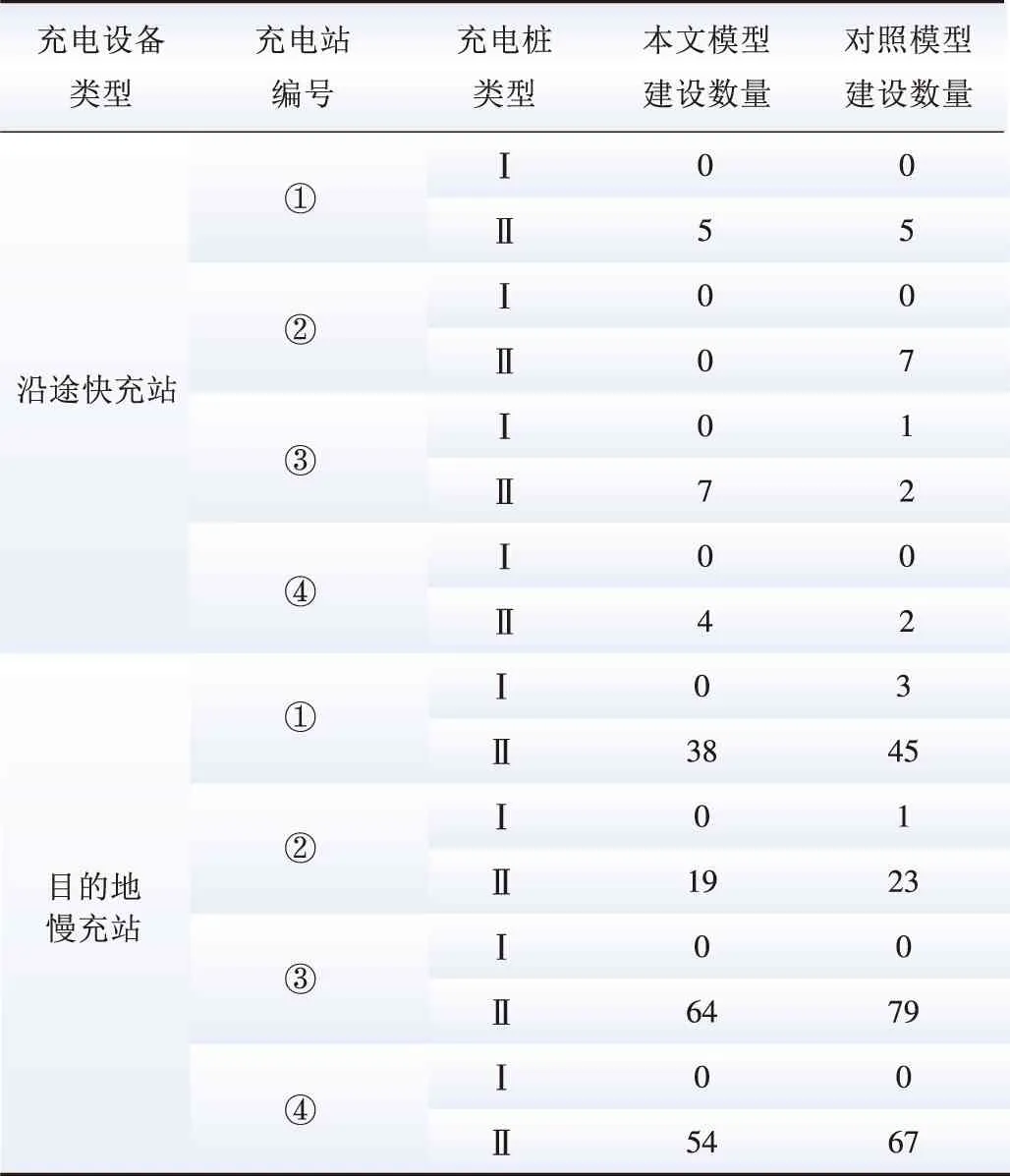
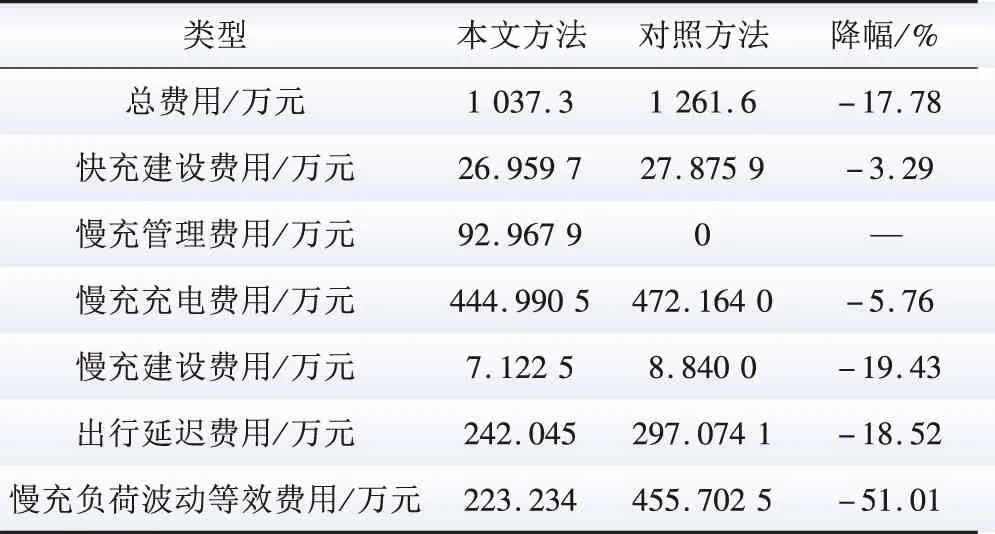
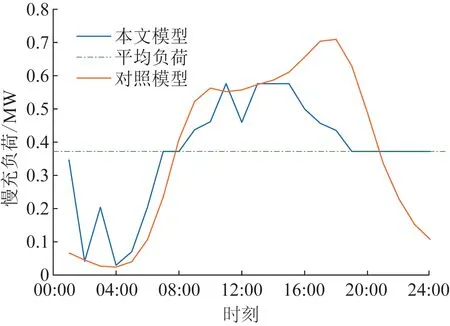
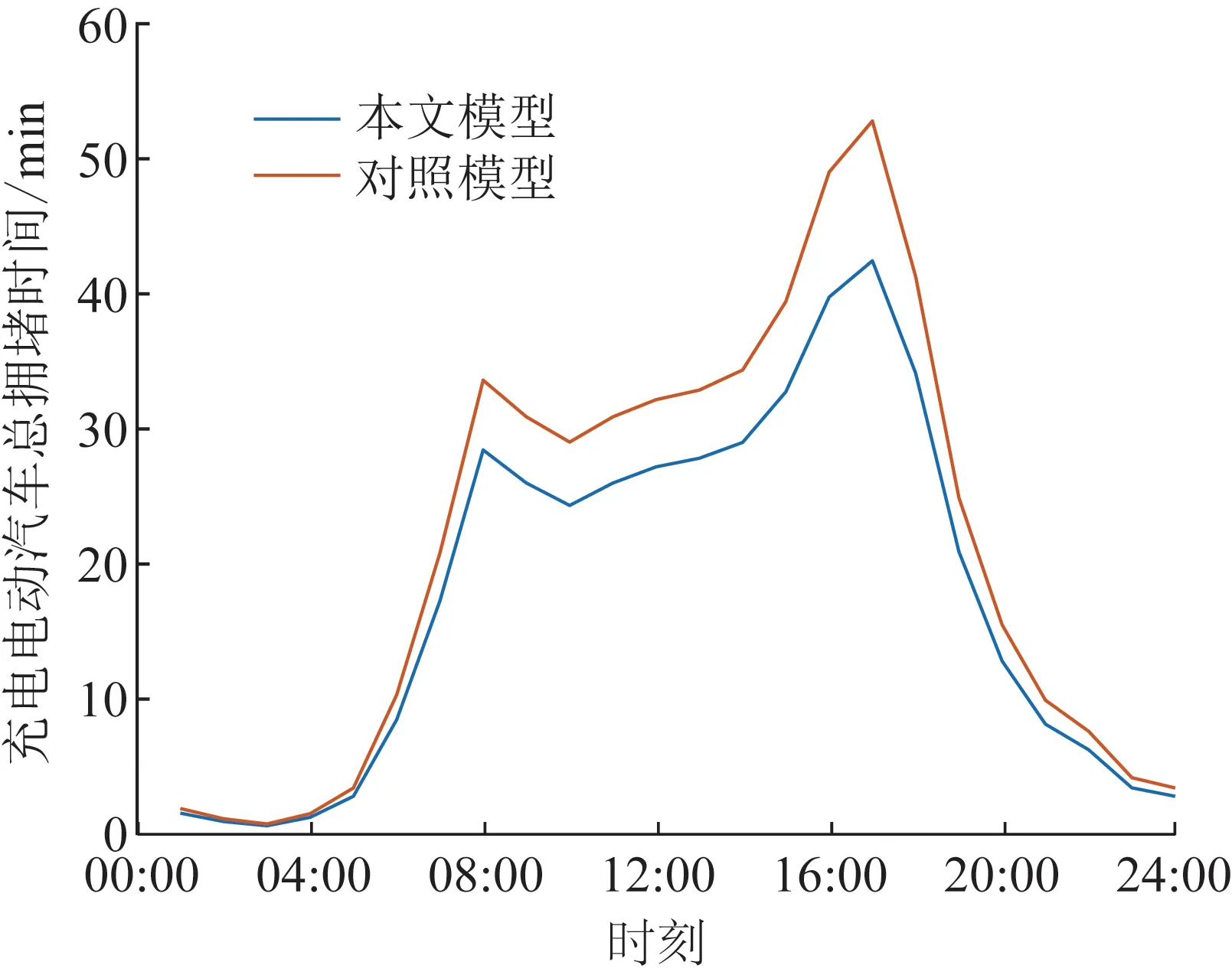
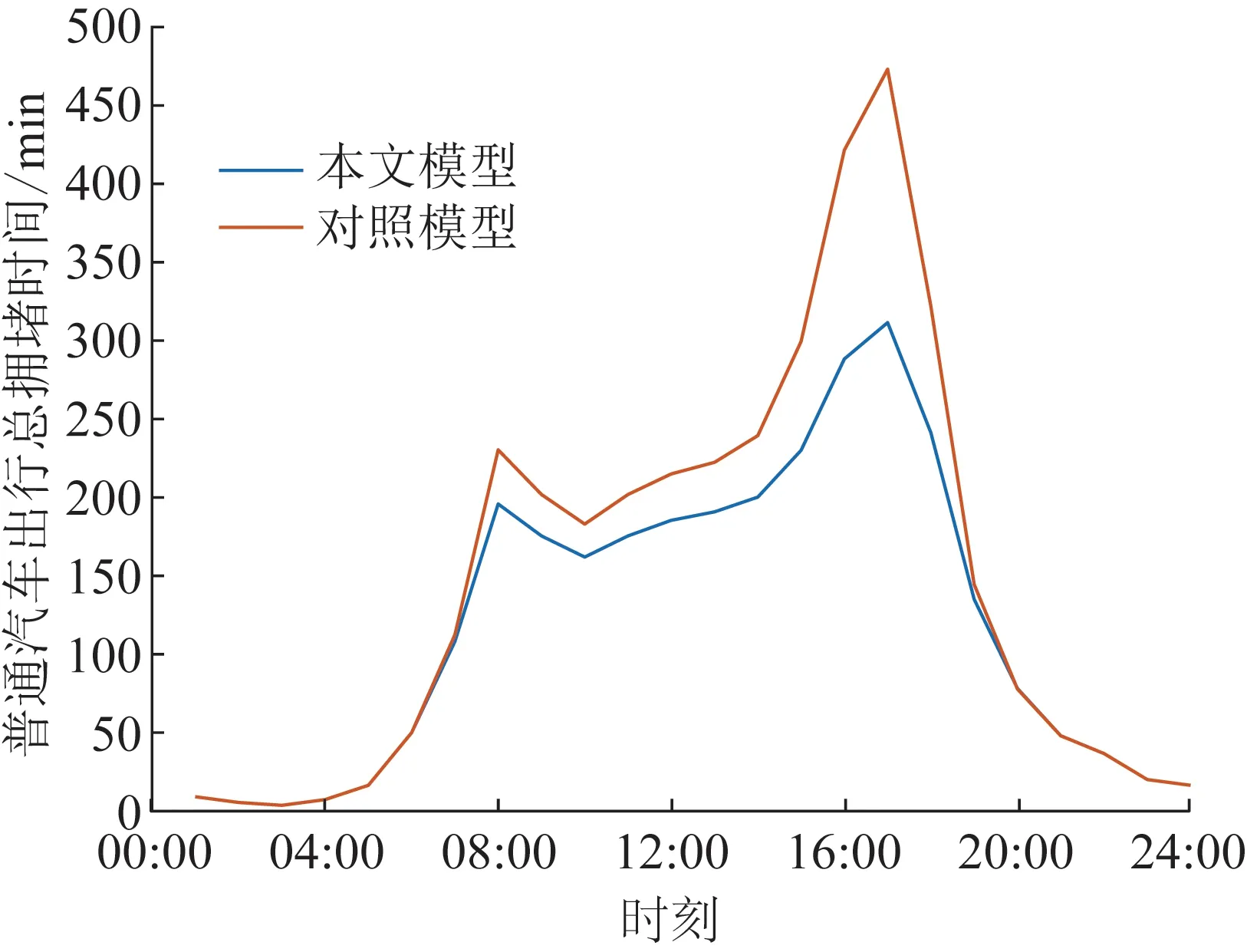
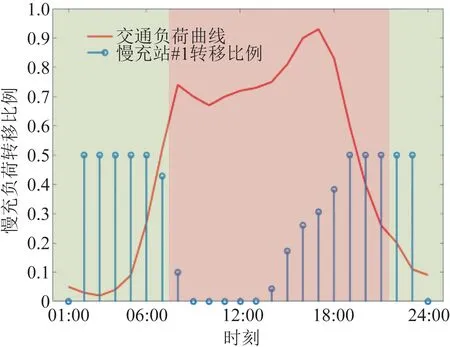
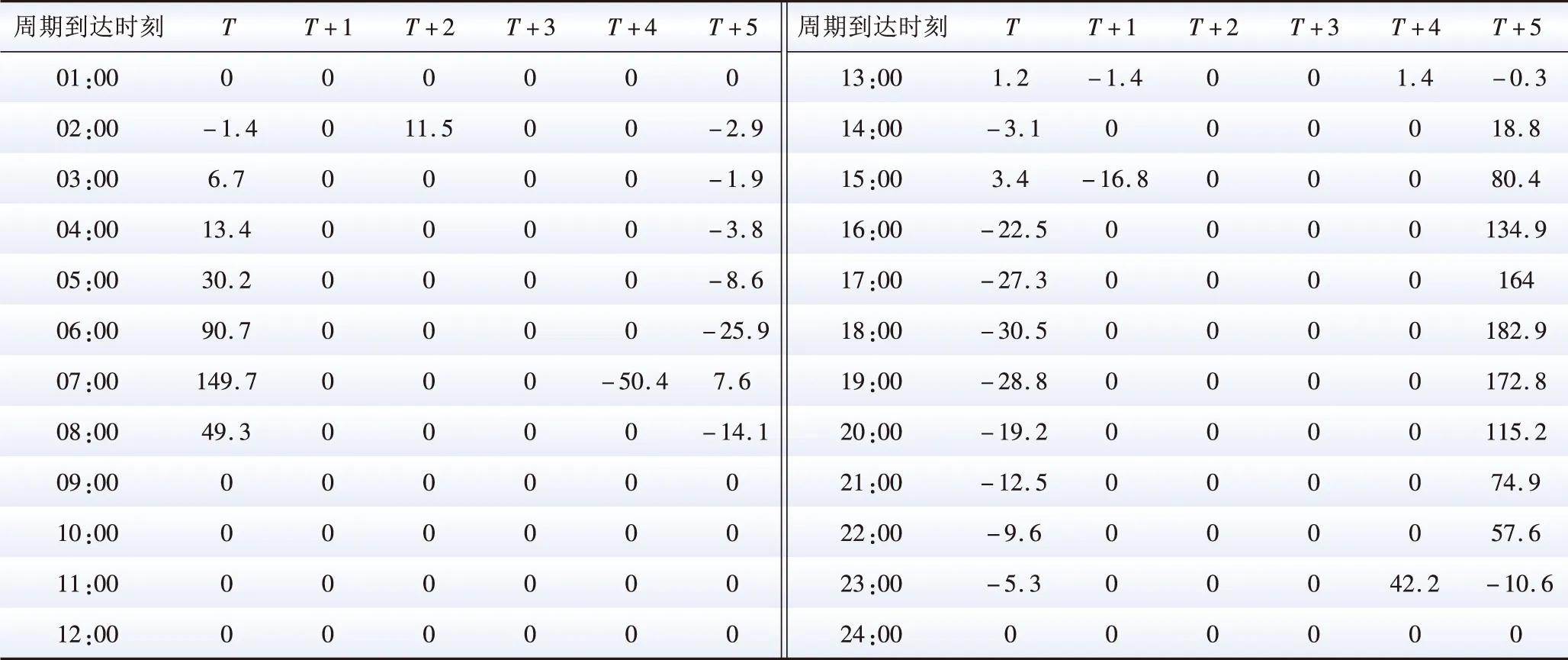
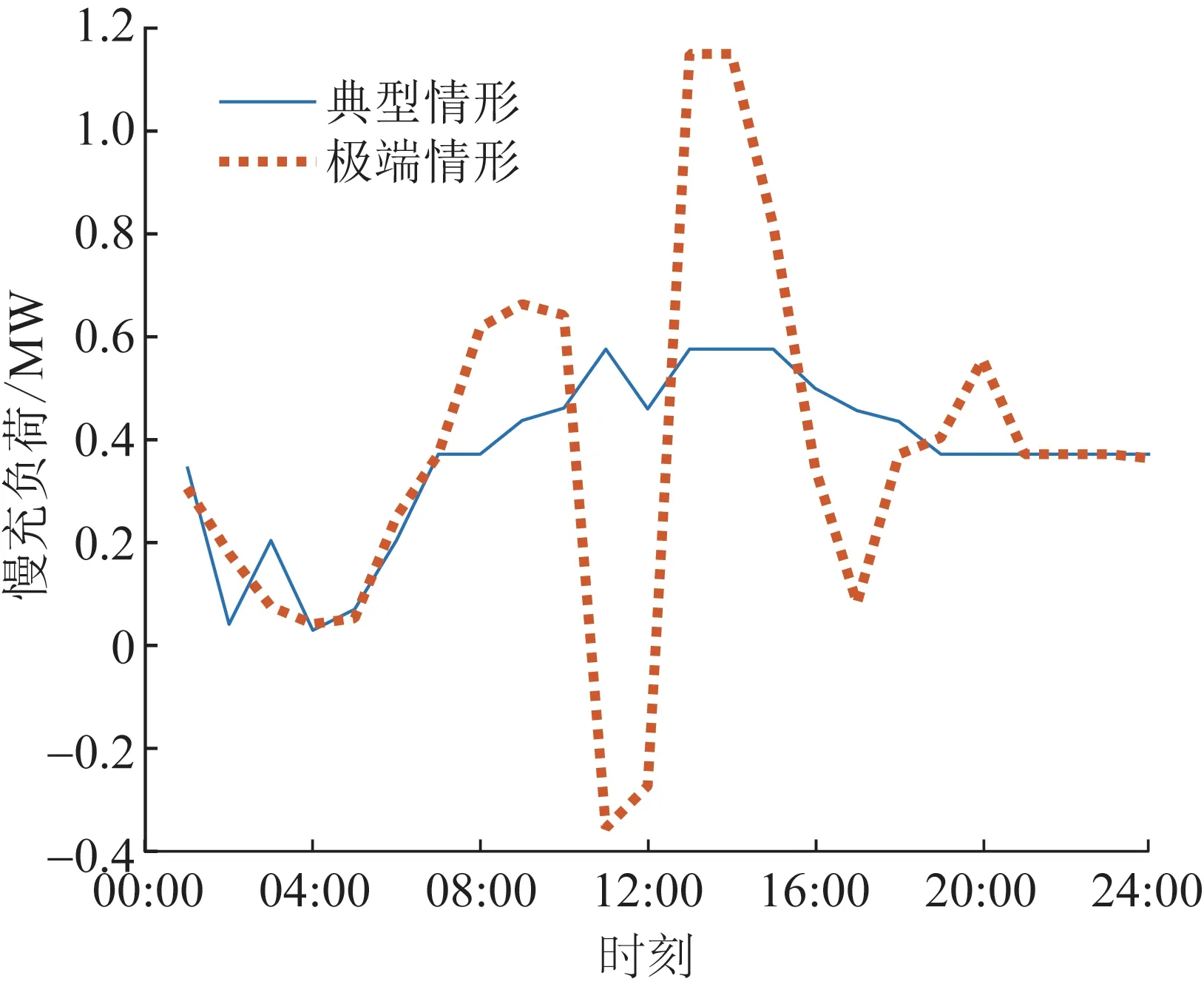
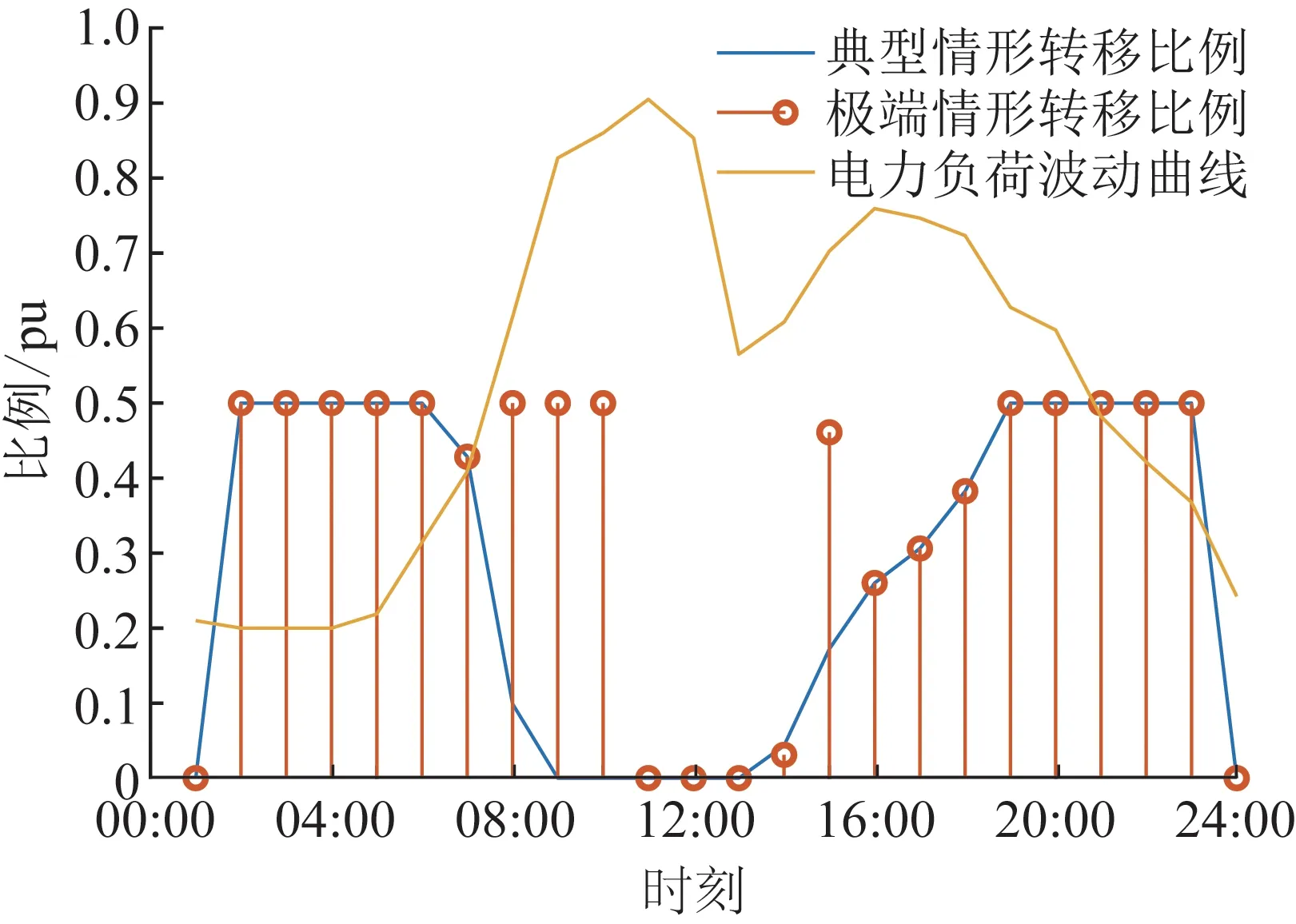
2)将在目的地停留时间超过调控时间周期t2且有意愿参与充放电管理的用户所对应的电动汽车充电需求视为可调慢充负荷,该部分待充车辆将会在调控周期t2后完成充电行为,以保证用户的正常用车需求,通常t1 为方便数学建模,定义负荷转移矩阵R如表1所示,其中行表示各场景负荷转移情况,列对应各相对调控时段的充放电功率。下标i表示各慢充站节点。 表1 电动汽车充放电管理慢充负荷转移矩阵Table 1 Slow charge load transfer matrix of EV charge and discharge management 由此,目的地慢充装置充放电管理措施的数学模型可表示为: 1)慢充负荷转移约束。 (10) 2)慢充站实际功率约束。 (11) 3)调控负荷比例约束。 αmin,ω≤αi,ω≤αmax,ω (12) 式中:αmax,ω、αmin,ω分别代表最大、最小可调控负荷比例,其值介于0~1之间。 4)充放电限度约束。 (13) 0≤Si,ω,h≤Si,ω,max (14) 式中:Si,ω,h为ω时刻到达的慢充车辆剩余荷电状态;Si,ω,max为ω时刻到达的慢充车辆的最大充电容量上限。值得注意的是,本文忽略电动汽车充放电时所产生的功率损耗,即充放电效率均为100%。 在前述第1节和第2节的研究成果基础上,本节提出基于流量均衡理论和电动汽车充放电管理的快/慢充电站规划模型。该模型以充电站建设费用、运行费用、交通网出行等效费用、慢充负荷波动等效费用最小为目标,考虑建设约束和运行约束,对沿途快充设备和目的地慢充设备进行合理配置。 本模型关注交通网部分的经济效益,从最优化系统的等年值经济效益出发,考虑沿途快充站的建设费用、目的地慢充站的建设费用、车辆出行拥堵费用、目的地慢充站充电费用、目的地慢充站电动汽车充放电管理费用、目的地慢充负荷波动等效费用,具体数学表达式如下: minF=ϑCcon+Cope (15) (16) (17) Cope=365×(Ctra+CenT+CTM+Cwave) (18) 式中:F表示系统的全周期经济费用;Ccon为系统建设费用;Cope为系统运行费用;ϑ 为等年值系数;r为折现率,通常取10%;N为机组寿命,本项目取10年,故通过计算ϑ 取0.162 8。 j∈ΩFC,k∈ΞFC (19) j∈ΩSC,k∈ΞSC (20) 3)车辆出行拥堵费用Ctra。 ∀ω,ε∈ΛOD (21) 4)目的地慢充站充放电费用CenT。 ∀ω,i∈ΩSC (22) 5)目的地慢充站电动汽车充放电管理费用CTM。 ∀ω,i∈ΩSC (23) 式中:κ为单位比例的充放电管理费用;αi,ω为当前时刻的慢充负荷实际调控比例。 6)目的地慢充负荷等效波动费用Cwave。 (24) 本模型的约束类型可按照阶段和对象分为设备投建约束、配电网运行约束、交通网运行约束3类,各约束详细的数学表达形式分述如下。 1)设备投建约束。 (1)投建数量约束。 x∈{FC,SC},Υ∈{ΩFC,ΩSC} (25) (2)慢充站投建功率约束。 i∈ΩSC,k∈ΞSC (26) (3)快充站投建功率约束。 (27) a∈Ωroad,i∈ΩFC,k∈ΞFC (28) 2)配电网运行约束。 (1)电力潮流约束。 (29) (30) (31) ∀ω,∀j∈Ωbus,∀ij∈Ωline (32) (2)安全稳定运行约束。 (33) (34) (35) (36) 3)交通网运行约束。 回顾第2节和第3节,交通网运行约束主要包括交通网的网络模型约束和电动汽车充放电管理措施约束,可归纳为: {式(1)—式(2), 式(4)—式(14)} 1)分段线性化方法。 由式(7)可知,BPR函数为高次非线性函数,利用分段线性化方法对其进行处理,可转化为如下等价表达式: (37) 式中:τm为ηm·δ的辅助变量;δ和ηm分别为辅助连续变量和二进制变量;M是一个较大的数。 2)大M法[11]。 (38) (39) 回顾式(24),式中存在的绝对值函数不利于快速求解最优解。本节引入二元变量λ+/λ-、辅助变量Φ+/Φ-对原式进行松弛处理如下: (40) (41) (42) (43) (44) (45) (46) 3)二阶锥松弛技术[12]。 回顾式(5)—(32),潮流约束为非线性约束,参照文献[13],本文采用二阶锥方法对其进行松弛,松弛后表达式为: (47) 式中:‖·‖2为二范数的数学表达形式。 至此,混合整数非线性模型已经转化为混合整数二阶锥问题,整体归纳如下: 本文采用IEEE 33节点配电网[14]与12节点典型交通网[15]耦合系统对所提规划方法进行仿真测试,拓扑结构如图1所示,空间位置的耦合信息如附表A1—A2所示,交通网的路况信息如附表A3所示。测试系统分别对4个沿途快充站和4个目的地慢充站进行规划,附表A4和附表A5分别给出沿途快充充电桩和目的地慢充充电桩的技术参数。此外,为了更好地反应用电量情况,参考文献[16],本文将电力负荷节点划分为工业、商业、居民3类,典型负荷序列如附图A1所示。交通网的出行需求信息如附表A6所示,各目的地慢充最大负荷信息如附表A7所示,用户出行的典型时序曲线如附图A2所示[1]。本文还对快/慢充站的充电费用予以考虑,4个快充站对应充电费用级别为35、35、10、10元;目的地慢充站采用峰谷电价收费,其中峰时段(08:00—21:00)充电费用为0.55元/(kW·h),谷时段(22:00—07:00)充电费用为0.35元/(kW·h)。充放电管理模型中,固定充电时间t1=3 h、调控周期t2=6 h。其他经济技术参数如附表A8所示。 图1 耦合测试系统示意图Fig.1 Diagram of coupling test system 为了验证本项目所提智能配电网充电站规划模型的先进性,本节设置对照模型:规划模型不考虑流量均衡理论,即所有交通用户选择负荷要求的最短路径通行,且模型不含电动汽车充放电管理策略,即所有目的地慢充用户都采用即到即充的被动充电模式。规划结果比较如表2所示,经济结果比较如表3所示。 表2 本项目模型与对照模型规划结果对比Table 2 Comparation of planning resultsbetween the project model and the control model 表3 本项目模型与对照模型经济指标对比Table 3 Comparation of economic results between the project model and the control model 分析表2和表3可得到以下结论: 1)考虑充放电管理措施有助于优化慢充桩投资且平抑慢充负荷的波动性。由表2可知,本文模型配置的慢充桩额定容量为1.575 MW,而若不考虑管理措施则需配置总容量为1.954 MW的慢充装置。对应的,如表3所示,投资费用降幅达19.43%。为了探究优化设备投资的根本原因并验证本文所提充放电管理措施的有效性,图2以①号目的地慢充站为例对比了本文模型和对照模型的充电功率曲线。由此可以得出,经过充放电管理,一天内的慢充负荷峰谷差减小,波动情况得到明显改善,慢充负荷波动等效费用削减比例高达51.01%;无管理下的充电负荷高峰(17:00—18:00)经过负荷转移措施尖峰得以消除,从而降低了负荷需求峰值,减少慢充设备的投资容量。 图2 慢充站充电功率曲线对比图Fig.2 Comparison chart of charging power curve of slow charging station 2)通过交通网通行情况的信息共享使用户达到混合用户均衡状态,有利于提高用户出行效率。图3和图4分别展示了CV和NV各场景下的出行拥堵总时间。通过观察可发现交通流量均衡模型可以降低出行车辆的拥堵时间,特别在出行高峰时段(17:00)缓堵作用尤为明显。表3给出了出行延迟费用这一量化指标,同比下降18.52%。 图3 CV出行总拥堵时间Fig.3 Total congestion time of CV travel 图4 NV出行总拥堵时间Fig.4 Total congestion time of NV travel 为了凸显本文所提基于负荷转移矩阵的充放电管理措施的有效性,下面以①号目的地慢充站为例进行分析,负荷转移比例与交通负荷曲线如图5所示,负荷转移矩阵如表4所示。 图5 ①号慢充站负荷转移比例与负荷曲线图Fig.5 Load transfer ratio and load curve diagram of slow charging station ① 图5中,红色区域为高电价时段,绿色区域为低电价时段。由结果分析可知,电动汽车充电负荷高比例转移主要发生在低负荷时段、高负荷时段、高电价近结束时段。这是由于低负荷与高负荷时段需要通过负荷转移来平抑电动汽车负荷波动性,高电价近结束时段可通过延迟充电降低用户的充电费用。由表4可知,清晨时段(01:00—08:00)电动汽车先充后放以应对白天期间的高目的地充电负荷;上午时段(09:00—13:00)基本不参与电动汽车负荷转移调度,由于到了下午时段用户的出行比例仍处于一个高峰状态,此时若进行负荷转移调度效果不明显;下午时段(14:00—20:00)充电负荷呈现高峰状态,此时通过负荷转移实现削峰效用,电动汽车体现先放后充的充电规律;此外,晚间时段(20:00—23:00)在高峰电价时放电,低谷电价时充电,以此降低充电费用,此外还增加深夜时刻的充电量,平抑慢充负荷的波动性。由此,可证明本文所提充放电管理策略的有效性。 表4 ①号慢充站负荷转移情况Table 4 Load transfer of slow charging station ① kW 此外,本文还讨论了在配电网处于极端高负荷情况下所提出的充放电管理措施运行机理。 图6比较了典型情况与极端情况下的充放电功率。当配网处于负荷峰值时(09:00—11:00),电动汽车在本文充放电管理措施调控下,向电网放电满足极端情况下的源荷供需平衡。虽然会使全周期的慢充负荷有剧烈波动,但维持配网安全运营更为重要。 图6 两种情况下慢充站充电功率曲线对比图Fig.6 Comparison chart of charging power curve of slow charging station in two cases 从图7可以看出,在极端高负荷时(07:00—09:00),本文充放电措施会引导大规模慢充负荷动作转移,这一现象表明本文所提管理措施能与配网进行有效互动。 图7 极端情况节点慢充站的负荷转移比例图Fig.7 The load transfer ratio diagram of the slow charging station under the extreme case 本文提出一种基于混合用户均衡理论和电动汽车充放电管理措施的智能配电网充电站规划模型,在该模型中提出一种基于负荷转移矩阵的充放电管理策略及其建模方法,为智能快/慢充站的合理规划提供技术支撑。经过算例仿真分析,得出以下结论。 1)本文所提规划模型能够实现智能交通网下沿途快充站和目的地慢充站的优化配置,相较于传统模式下的规划模型投资与运行的总费用显著降低,降幅达17.78%。 2)本文所提充放电管理策略有助于优化慢充设备的投资并大幅降低因充电负荷波动对配电网带来的冲击。根据算例分析可知,负荷波动等效费用由455.7万元降低至223.23万元,降幅达51.01%。 然而,本文的研究仅局限于以电能为动力源的新能源汽车。当前,综合能源系统的规划与布局正如火如荼地开展,以天然气等新能源的绿色出行工具也将迎来新的发展高峰。因此在后续的研究中我们将重点考虑多种能源形式驱动的新能源汽车充放能管理策略及其综合能源系统拓展规划方法。
3 基于流量均衡理论和电动汽车充放电管理的快/慢充电站规划模型及其求解
3.1 目标函数
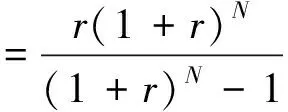
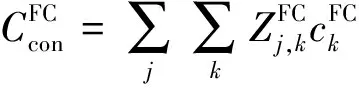
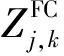

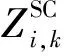
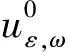
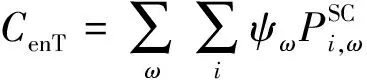
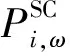
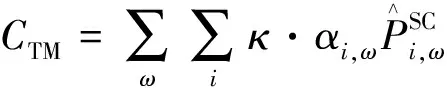
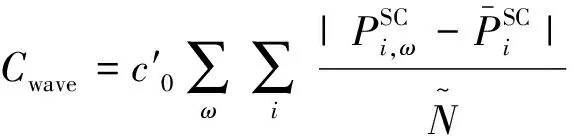
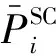
3.2 约束条件
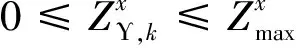
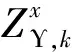
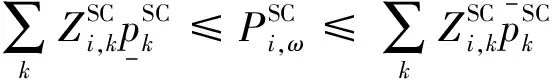
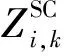
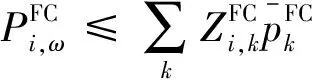
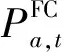
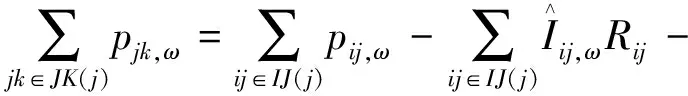
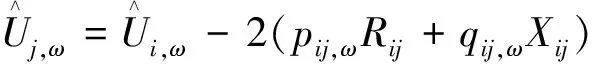
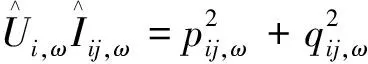
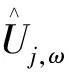

3.3 模型线性化方法
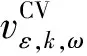
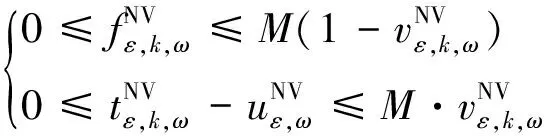

4 算例分析
4.1 系统描述
4.2 规划结果及分析
5 结 论
