数据驱动的配电台区源荷污染源群体谐波排放建模
2021-08-11张孟琛林丽娟孟菁牛益国王珺石磊磊
张孟琛,林丽娟,孟菁,牛益国,王珺,石磊磊
(1.国网冀北电力有限公司秦皇岛供电公司,河北省秦皇岛市 066004;2.电力电子节能与传动控制河北省重点实验室(燕山大学),河北省秦皇岛市 066004;>3.国网河北省电力有限公司邢台供电分公司,河北省邢台市 054001)
0 引 言
近年来,含电力电子接口的分布式发电和低压负荷设备得到越来越多的应用[1-2],使配电台区谐波源呈现高密度、分散化、全网化的特点[3-4]。尽管单个电力电子非线性负荷谐波排放量并不显著,但大量谐波叠加对电网产生的影响不容忽视[5-6]。由于分散谐波源数量多、个体容量小、运行随机性强,建立反映谐波源随机行为的配电台区节点群体谐波排放模型十分必要。风、光等分布式电源的运行主要受天气影响,其行为特性通常具有一致性,群体谐波排放模型较容易建立。而非线性负荷设备启停状态随机,群体模型不易表征。因而,建立包含分散化源、荷的配电台区群体谐波排放模型既有实际意义又具有挑战性。
评估用户对电网的谐波排放水平,需要建立系统谐波阻抗和用户谐波模型。文献[7-10]分别从“注入法”、回归分析、支持向量机等角度进行了系统谐波阻抗计算,相关方法比较成熟。用户谐波源建模方面,恒流源模型是一种典型形式,但不能体现电压的影响[11]。负荷谐波耦合导纳矩阵模型[12]虽然能体现谐波电压的影响,但依赖负荷等值电路结构和参数。基于神经网络模型和频域卷积模型[13-14]的谐波源建模过程复杂。诺顿(Norton)模型从外部特性上进行等效,不需要对谐波源的内部构成机理进行复杂分析[15],仅需要考虑同次谐波电压与电流之间的影响,广泛应用于工程实际[16-17]。
基于历史用电数据的挖掘分析是获得用电行为的有效手段[18]。文献[19]考虑新型场景划分与时序相关性,提出一种光伏出力时间序列模拟方法。文献[20]用蒙特卡洛法模拟居民负荷投切随机性。文献[21]从智能电表中提取不同粒度用电数据特征,用于识别社会人口消费的统计信息。文献[22]考虑居民用电因素,建立了民用负荷用电行为学模型。文献[23]将谐波耦合主导模型与行为学模型相结合对居民负荷进行谐波评估。上述文献利用马尔科夫链(Markov chain, MC)、非侵入式负荷监测(non-intrusive load monitoring,NILM)等数据挖掘技术对设备用电行为进行了分析。MC在利用有限历史数据进行时间序列建模方面具有明显优势;而NILM技术在获取用电设备行为方面,只需将负荷监测装置安装在用户供电入口处,通过监测并分解用户用电数据,就可辨识各用电设备启停工作状态,具有很强的经济性和实用性[24-25]。
由上述分析可知,随着分散化电力电子设备高比例接入配电网,建立谐波源群体排放模型十分必要。但如何客观真实反映大量用户行为、保障模型的有效性是问题的关键,现有研究未能很好解决。本文利用NILM技术和MC模拟提出一种数据驱动的谐波污染源群体谐波排放水平建模方法。以NILM技术获取的不同设备任意时刻启停状态辨识数据为驱动,建立各类负荷各时段接入数量动态变化的时序特性模型,将该模型代入谐波诺顿等效电路,得到集群谐波排放模型。最后,用算例分析验证方法的有效性。
1 配电台区设备的谐波模型
配电台区典型分散谐波源负荷包括经电力电子接口供电的家用或商用电器,如电视机、电冰箱、空调、计算机等,以及变频调速电机等工业设备。由于谐波源负荷设备种类繁多,谐波排放机理和排放特性各异,本文采用诺顿电路的统一形式表征谐波等效模型,并通过试验手段获得等效参数。另外,光伏发电是配电台区典型分布式电源设备,光伏逆变器工作原理一致,其谐波模型可通过机理分析建立。
本节建立配电台区典型谐波源设备谐波模型,为建立配电台区群体谐波模型奠定基础。
1.1 谐波源用电设备的谐波诺顿模型
谐波源用电设备各次谐波电流对外电路而言可等效为一个诺顿电路,如图1所示。谐波诺顿模型参数可通过波动试验法求取[11]。设典型谐波源用电设备种类数量为N,构造2次不同的电压条件,当2次电压条件间的差异能足够引起谐波电流发生变化时,可通过式(1)、(2)计算得到第n(n∈N)类谐波源设备的谐波阻抗和谐波电流源参数。其中2次不同电压条件的基波电压相角需要一致。
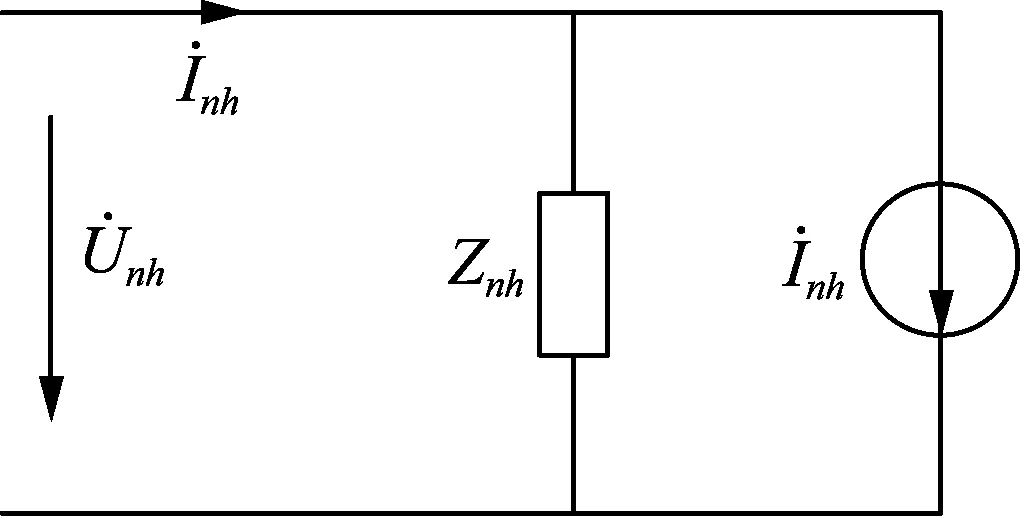
图1 电力电子设备谐波诺顿模型Fig.1 Norton equivalent harmonic model of power electronic equipment
(1)
(2)

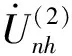
1.2 分布式光伏逆变器的谐波模型
光伏逆变器内部构造相近,谐波含量受运行状态和内部参数影响大,宜采用机理模型。太阳辐照度和光伏板温度对光伏输出特性影响较大[26],是谐波模型的主要变量。光伏组件实际辐照度和温度与标定测量的转换公式如式(3)所示。
(3)
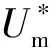
由此,可得到逆变器直流侧电压Udc为:
(4)
式中:Ns为光伏组件串并联数量。
逆变器开关调制产生的高次谐波可由LCL滤波器滤除,一般只需要考虑死区引起的低次谐波,其电压表达式如式(5)所示[26]。
(5)
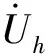
(6)
式中:ZL1、ZL2、ZC为LCL滤波器参数。
联立式(3)—(6)可得分布式光伏谐波模型。
2 数据驱动的用电行为MC建模
在一天的不同时段,用户各类用电设备使用情况存在随机性,NILM可以获得设备启停的大量实际数据,这些数据反映了用户设备启停随机过程的潜在行为规律。本节以NILM监测数据为驱动,建立谐波源设备启停状态的MC随机模型,反映各时刻配电台区各类谐波源设备的启停状态,结合第1节用电设备谐波分析,得到配电台区同一类设备整体谐波排放水平,再通过叠加不同类型设备群体谐波电流,最终得到整个配电台区所有谐波源负荷群体的谐波电流排放总量。
2.1 设备启停状态的NILM监测与表征
NILM分解过程主要包含事件探测、特征提取和负荷辨识等环节[27],典型实现结构如图2所示。通过NILM对用电数据进行分解,可得到主要用电设备在全天任意时刻的启停状态。
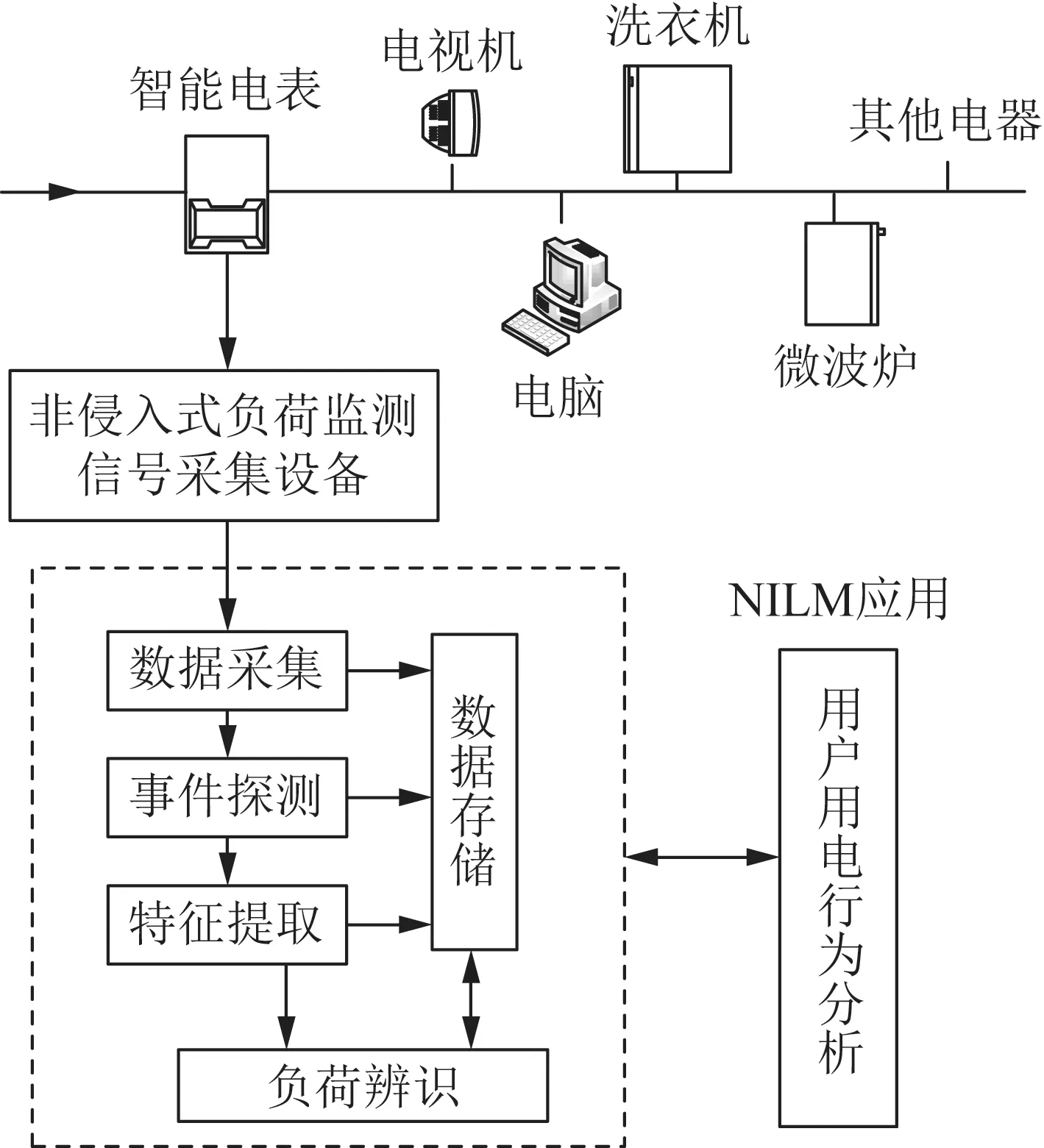
图2 NILM框架示意图Fig.2 Schematic diagram of NILM framework
图3为用户NILM分解结果,图中粗线表示设备处于运行状态,细线表示设备处于停机状态。
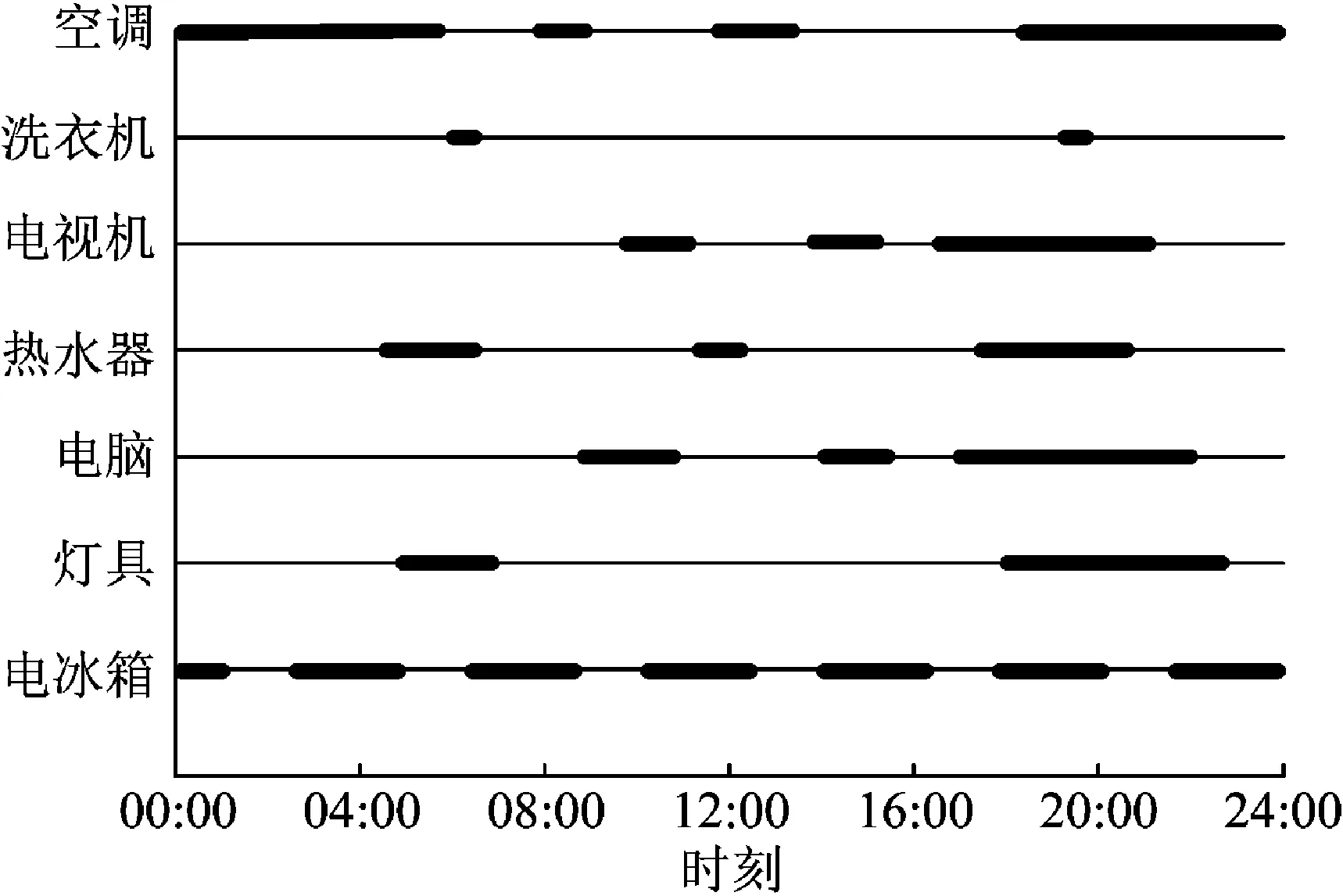
图3 居民用户NILM分解结果示意图Fig.3 Schematic diagram of NILM decomposition results of residential users
考虑到不同设备工作周期的持续时间差异,以10 min为时间间隔记录各类谐波源用电设备的启停状态,得到设备启停状态矩阵S,如式(7)所示。
(7)
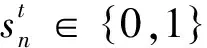
除具有开关状态的用电设备外,变频洗衣机、变频冰箱和空调等变频设备在运行过程中存在功率连续变化的特性,但其谐波含量几乎不受功率变化的影响,即功率变化过程中谐波含量几乎不变[28]。因此,具有连续多运行状态的非线性负荷仍可按启/停两状态处理。
2.2 用户集群设备启停行为的MC建模
MC是基于有限历史数据来模拟时间序列按条件概率相互依赖的随机过程[25,29]。用电设备的启停状态是随机事件,本文以各类用电设备各时刻开启数量作为状态量,采用马尔科夫过程对开启数量的概率进行建模。由于用户用电行为在一天内具有时段差异性,某些设备在某些时段使用频繁,而在另一些时段使用率极低。考虑到NILM存在辨识误差,尤其在设备启停数量大、变化剧烈的时段,误辨识数量也会增大。为防止马尔科夫模型中概率转移矩阵传递中误差的累积影响,本文将一天分成若干时段,分别建立不同时段的马尔科夫模型,然后通过时段间状态量初值和终值的衔接形成全天的模型。
设某类设备总数量为M,则任意时段d内同时开启的设备数量取值范围为[0,M],该类设备开启数量的总状态数为M+1。设某类设备开启的初始状态概率分布为:
(8)
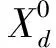
取10 min为状态转移时间步长,则状态转移事件“从t时刻开启的设备数量i转移到t+1时刻开启的设备数量j”的状态转移条件概率值Pij,可以通过NILM监测的历史数据中统计t到t+1时段从状态i的所有状态转移中转移至状态j的时间发生次数所占比值来求得。也就是用有限数量的历史统计数据来近似逼近其概率值,计算方法如式(9)所示。
(9)
式中:nij为d时段对应的NILM监测历史数据中t到t+1时刻从状态i转移到状态j的次数;J为状态转移的总数。
d时段内设备的开启台数在所有情况下转移概率Pij构成的状态转移概率矩阵Pd,如式(10)所示。
(10)
状态转移矩阵Pd为(M+1)×(M+1)阶,其元素为马尔可夫链的单步转移概率,各行元素之和为1。
由全概率公式,若已知t时刻设备开启数量的状态分布,则可得t+1时刻的概率分布为:
P(Yt+1=i)=P(Yt+1=i|Yt=0)×P(Yt=0)+
P(Yt+1=i|Yt=1)×P(Yt=1)+
…
P(Yt+1=i|Yt=M)×P(Yt=M)
(11)
由d时段内t时刻设备开启状态概率分布及单步状态转移矩阵Pd,可得t+1时刻设备开启状态的概率分布:
(12)
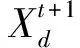
同时,由K-步转移概率性质可知,K-步转移矩阵是其之前所有转移矩阵之积,如式(13)所示。
(13)

(14)
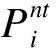
2.3 群体谐波排放水平估计
按上述方法得到配电台区各类用电设备各时刻开启数量期望值,再根据1.1节中式(1)和式(2)得到各时刻台区某类用电设备的谐波电流排放量,最终得到该类设备群体的谐波电流排放水平。
在得到单一类型设备的群体谐波电流排放水平后,通过叠加不同类型设备的群体谐波电流,再叠加对应时刻光伏电源的谐波电流,最终得到整个台区所有谐波源负荷群体的谐波电流排放总量。集群的h次谐波电流为:
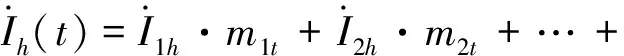
(15)
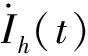
谐波源及系统侧的h次谐波等值电路如图4所示。电源侧由系统等效谐波阻抗表示,谐波源均由谐波诺顿等值电路表示。
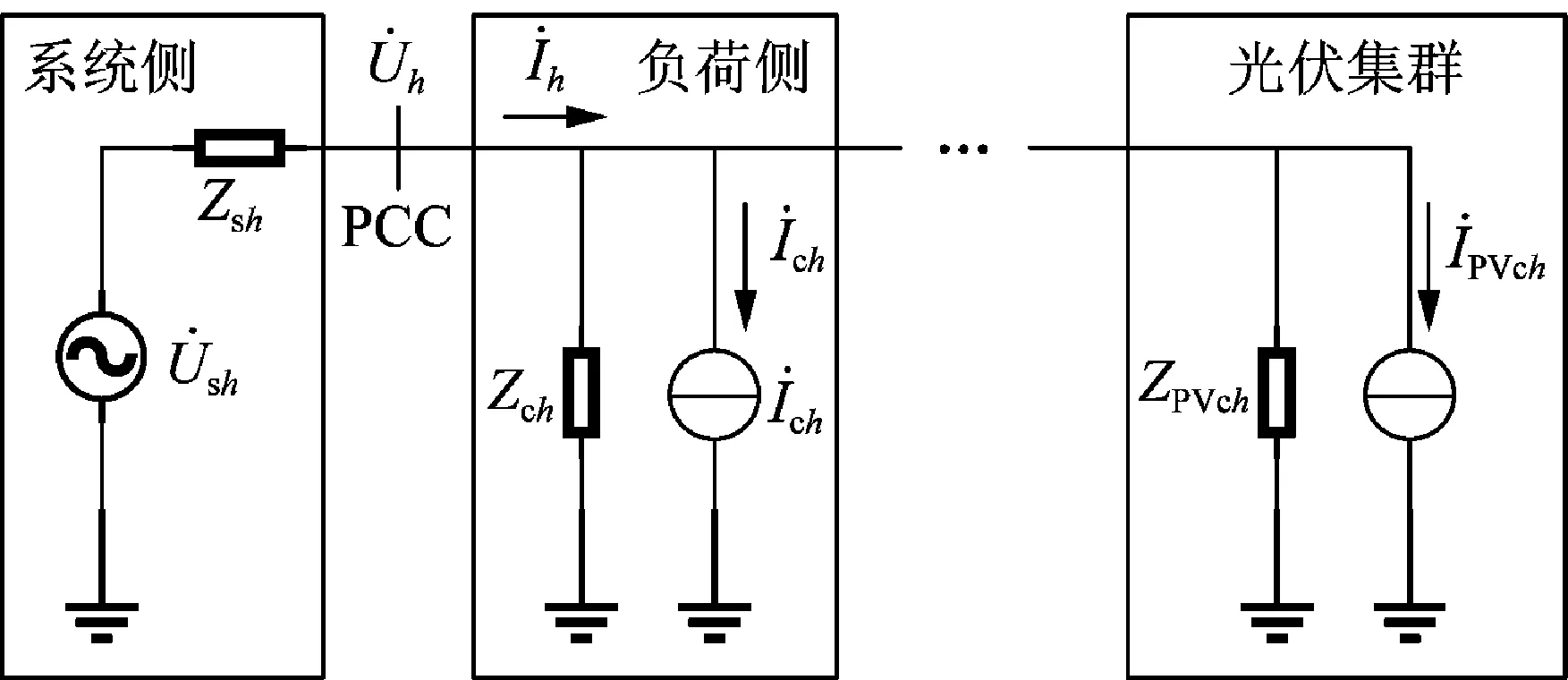
图4 谐波源及系统侧谐波等值电路Fig.4 Harmonic source and system-side equivalent harmonic circuit
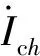
3 配电台区谐波排放水平动态建模流程
上述方法以NILM对设备启停的辨识数据为驱动,建立状态转移概率及初始时刻的状态概率分布,并通过MC模拟得到不同时段上各时刻设备开启数量的概率分布。根据开启数量的概率分布求期望从而得到各时刻不同类型谐波源设备开启数量的状态量。将设备开启数量代入相应类型的谐波模型,得到负荷设备谐波总排放水平;再将配电台区光伏的谐波排放加以考虑,可得到整个配电台区各时刻的谐波排放。
配电台区群体谐波排放水平建模方法的步骤如下:
步骤1:单一谐波源设备诺顿模型参数求取。通过波动试验法构造2次不同的电压条件,计算得到各种类单一谐波负荷设备的谐波电流源参数。
步骤2:非侵入式用电数据监测分解。根据各用户智能电表监测的用电数据,采用NILM技术对其进行非侵入式负荷分解,获得负荷的启停状态矩阵S。
步骤3:负荷同时开启数的MC转移模型。根据步骤1的分解结果,按照不同月份λ,不同时段d建立相应MC状态转移概率矩阵Pd,模拟每种负荷接入电网数量的变化过程。
步骤4:根据某时段设备投入数量和不同种类设备的谐波诺顿模型,得到该时段配电台区总谐波排放水平;逐时段进行分析可形成谐波排放估计曲线。
步骤5:叠加分布式光伏电源谐波污染。通过当地气象局的太阳辐照度Sr、光伏板温度Tr,按照所建立分布式光伏电源谐波模型,估算分布式光伏逆变器排放的谐波污染,最后与负荷谐波排放量相叠加得到地区总谐波排放水平估计曲线。
配电台区群体谐波排放水平评估方法流程如图5所示。
图5 配电台区群体谐波排放水平评估方法流程Fig.5 Flowchart of evaluation method for group harmonic emission level in station area
4 算例分析
本节分为2个算例,第一个算例是以配电台区内某类用电设备为例模拟一段时间内设备运行情况,第二个算例是在第一个算例基础上利用谐波叠加方式估计配电台区不同类别用电设备群体谐波排放水平。选取配电台区以北方城镇一居民小区实际情况为例进行分析。
4.1 用电行为模拟结果
负荷曲线来自当地电网公司,这里使用的是2019年5月份的用电功率数据,每隔10 min记录一次当前智能电表功率值。以配电台区的变频空调总体负荷为例,模拟用电设备不同时段的运行台数,并对比分析了蒙特卡洛模拟法。
5月份某两层楼08:00—14:00时段对应的状态转移概率矩阵为:
(16)
可以看出,矩阵非零元素主要集中在主对角线附近,且主对角元素明显大于同行其他元素。因此认为,从一个状态转移到与原状态相同或邻近状态的概率要远远大于其他状态。这也表明了负荷启停行为具有马尔科夫性。
时段08:00—14:00内配电台区变频空调负荷总开启台数模拟结果如图6所示。
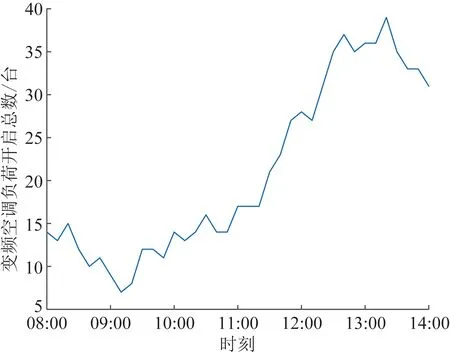
图6 时段08:00—14:00变频空调负荷开启总台数变化Fig.6 Changes of the total number of inverter air-conditioners during 08:00-14:00
基于各种类负荷设备的谐波Norton模型,由马尔科夫模拟得到各时刻负荷设备开启总台数,两者结合可得各类别负荷各时刻总的谐波排放水平。基于Fluke 434电能质量分析仪测量各电器的相关数据,由可编程交流电源产生标准余弦波和带有5%背景谐波的平坦波测量不同条件的电压波形[11],建立谐波Norton模型。以同类但不同型的变频空调负荷设备为例,3次谐波Norton模型参数如表1所示,而对于其他谐波次数和其他负荷,获取方法一致。本文在已知配电台区用电设备配置的情况下进行分析,在附录图A1中给出了不同型号变频空调启停曲线。
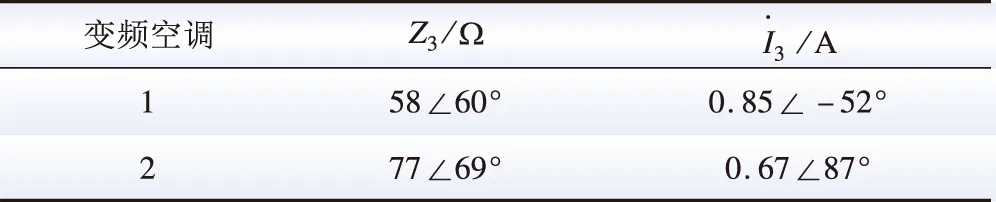
表1 变频空调3次谐波Norton模型参数Table 1 Norton model of the 3th harmonic in inverter air-conditioners
配电台区总的谐波电流在时段08:00—14:00内的排放水平估计结果如图7所示。由图7可知,配电台区内的变频空调在时段内总谐波电流排放量随机波动,3次谐波电流相对于5次谐波幅值较大,两者整体的变化趋势与配电台区内变频空调设备开启数量成正相关;在中午12:00—13:00之间谐波电流幅值较大,符合配电台区内负荷设备总体用电情况。
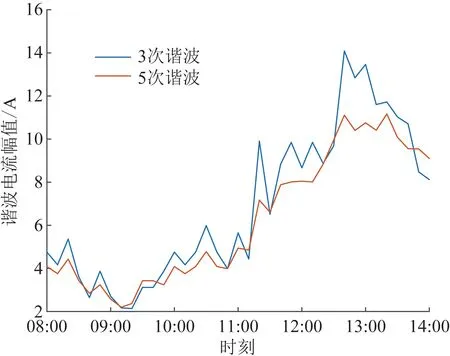
图7 变频空调负荷总谐波电流变化Fig.7 The change of total harmonic current of inverter air-conditioners during the period
为验证本文所提非侵入式负荷分解结合MC动态模拟方法的优势,将本文方法与文献[23]中所提到的“自下向上”的谐波评估方法作比较。文献[23]中采用蒙特卡洛法模拟负荷开通的时刻与持续运行时间,通过概率量化配电台区内负荷设备运行情况来决定负荷的开启与否。在本文同样的实验背景条件下,按照文献[23]所提供的方法对配电台区内所有变频空调负荷设备的谐波电流进行估计,结果如图8所示。两种方法评估结果的均值和标准差如表2所示。从结果来看,两种方法整体结果较为接近,MC法对一天各时刻变化的刻画更明显。
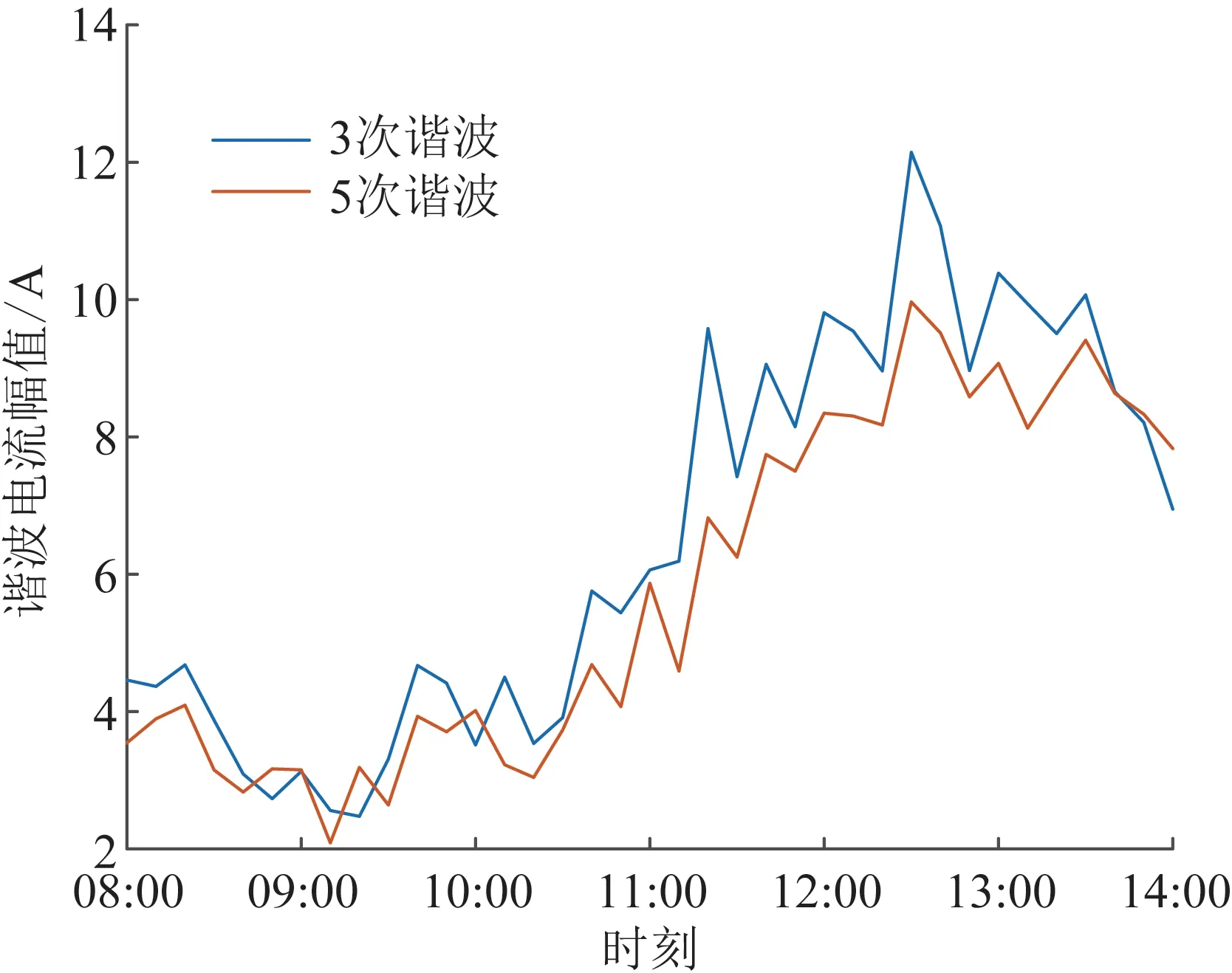
图8 蒙特卡洛法对变频空调负荷谐波电流预测结果Fig.8 Monte Carlo method for forecasting total harmonic current of inverter air-conditioners
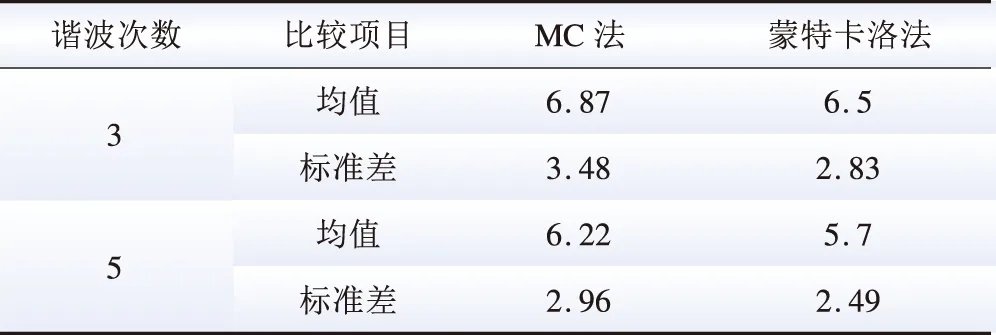
表2 两种方法评估结果均值和标准差Table 2 Comparison of the simulation results with the mean, standard deviation of measured results
本文方法在保证要求估计精准度的同时实现了模型输入参数更易获取的目的,而基于蒙特卡洛法模拟的估计方法则需要配电台区设备用电行为时间概率的统计数据,评估计算过程较为繁琐。
4.2 配电台区内谐波负荷群体估计结果评价
采集配电台区出口3次和5次谐波电流,测量5月份的谐波数据,每隔10 min记录一次,一天共得到144个电流采样点。将本文方法的模拟结果与现场实际测量结果进行比较,结果如图9所示。由于本文仅考虑了配电台区内民用负荷常见电力电子负荷设备,图9(a)中模拟结果较测量结果整体偏小。从波形整体趋势上看,3次谐波电流模拟结果与实际值变化趋势较为一致,谐波电流幅值最大值约为25 A,最小值为7.6 A,其电流实测数据的平均值最大值28 A、最小值8.6 A接近实际水平。另外,从图9中可看出时段19:00—22:00谐波污染排放明显高于白天时段,这与用户用电习惯相吻合。图9(b)中模拟结果5次谐波电流幅值最大值13.8 A、最小值8.1 A,对应的电流实测数据的平均值最大值为13.0 A,最小值为7.4 A。
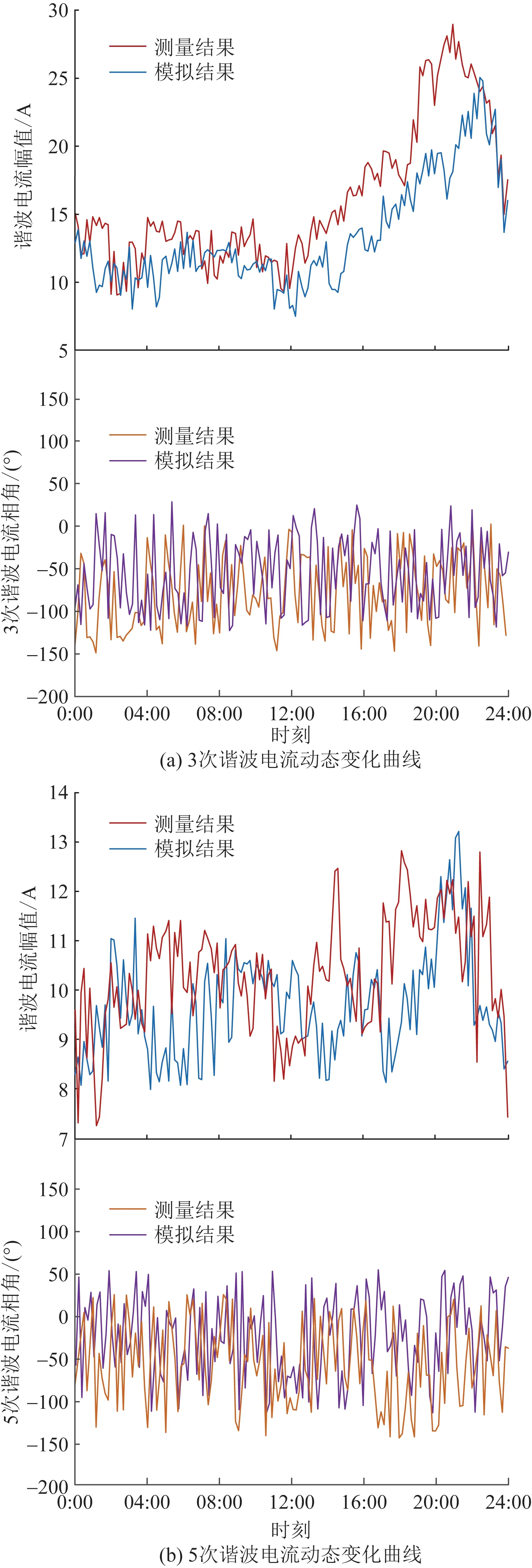
图9 谐波电流排放动态变化曲线Fig.9 Dynamic emission curve of harmonic current
表3给出了现场实际测量结果和模拟结果之间均值以及标准差的对比情况。3次、5次谐波电流实际测量结果与模拟结果之间均值的相对误差分别为0.184和0.176,说明本文方法对于3次、5次谐波估计结果较为准确,5次谐波电流估计结果与实际值更接近。但从3次、5次谐波电流实际测量结果与模拟结果之间标准差来看,5次谐波标准差较大,说明5次谐波估计结果波动性较3次谐波更大,主要原因为谐波次数越高,其幅值的变化范围小且随机变化性更强。通过本文所提方法的仿真结果与实测值的对比,验证了本文所提方法能够对分散化谐波源进行有效的谐波估计。
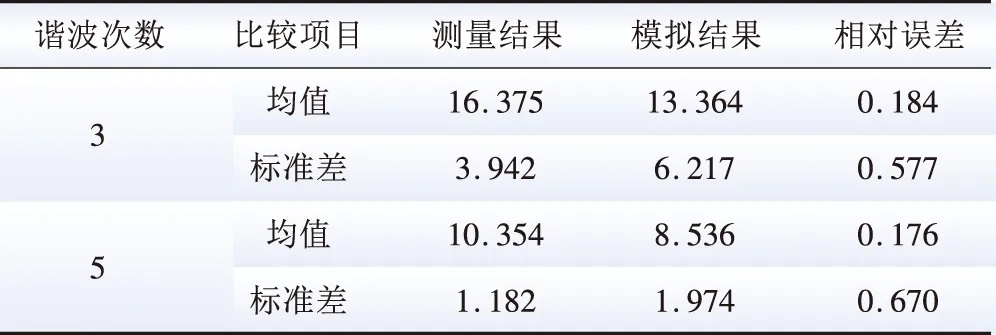
表3 测量结果与模拟结果的均值和标准差对比Table 3 Comparison of the simulation results with the mean, standard deviation of measured results
5 结 论
本文提出一种数据驱动的分散化源荷污染源群体谐波排放水平评估方法。通过试验法建立典型负荷类型的谐波Norton等效电路,并以NILM辨识的用户设备启停状态数据为驱动,利用 MC模拟建立各类负荷接入数量动态变化的时序模型,得到集群谐波排放模型。可得如下创新性结论:
1)提出基于NILM的MC动态模拟方法,实现了对负荷设备启停数量变化在时序上的动态模拟。该方法充分利用了电网监测系统的大数据技术,可有效对用户用电行为进行分析。同时,与蒙特卡洛方法对比验证了MC动态模拟方法在时间序列模拟上具有明显优势。所提上述用电行为建模方法为进一步谐波预测提供依据。
2)提出基于数据驱动的配电台区污染源群体谐波水平建模方法,为配电台区分散谐波源产生的谐波污染难以有效估计问题提供了新的解决思路。该方法适应了智能居民楼宇的发展趋势,充分利用智能化的数据采集和分析系统,使得计算过程更为简便,有效解决了大量分散谐波源群体谐波估计问题。
算例结果表明,本文方法能有效估计配电台区设备的集群谐波排放水平,对工程实际有一定指导意义。
