基于迁移学习的电能替代节能量在线估计方法
2021-08-11梁俊宇杨洋李怡雪舒杰
梁俊宇,杨洋,李怡雪,舒杰
(1.云南电网有限责任公司电力科学研究院, 昆明市 650214;2.中国科学院广州能源研究所,广州市 510640)
0 引 言
以煤为主的能源结构方式是导致我国当前环境问题的主要原因,随着环境污染问题的日益突出,亟需进行能源供给与消费结构的转变,实现清洁化的能源生产与消费。在我国,电能替代发展战略由国家电网有限公司于2013年提出。2016年国家发展改革委、能源局等部委联合发布了《关于推进电能替代的指导意见》。同年,中国南方电网公司发布《南方电网公司电能替代工作指导意见》,大力推进电能替代工作。电能替代是在能源消费市场上,以清洁电能代替污染严重的煤、油等化石能源。电能替代涉及工业[1-2]、商业[3]、农村[4-5]、家庭[6]等能源终端消费领域,具体包括工业用热/冷、电动车、轨道交通、港口岸电、家庭用热/冷等形式,替代面广、推广潜力巨大[7]。随着清洁能源发电在全社会用电量占比的增加,电能替代将成为我国能源结构优化的重要途径,对集中脱碳控碳及防治大气污染等具有重要意义[8],有利于实现我国2060年碳中和战略目标。从经济性方面考虑,电能替代技术可以提高能源转化效率,实现经济效益的提升[9]。
合理准确的电能替代节能量评估对电能替代项目推广有重要意义[10]。现有的文献已经从不同领域对节能量计算方法开展了研究。文献[11]基于典型冷水机的数学模型提出了冷水机组节能量计算方法,其建模数据需尽可能包含冷水机组实际运行的各负荷范围及工况。文献[12]考虑节能技术改造前的当日室内累计冷负荷和当日室外平均干球温度,提出了基于相似日法的建筑空调水系统节能量计算方法,提高了节能量计算的鲁棒性。文献[13]结合印染企业的实际情况,建立了印染企业的能源效益测量方法,重点考虑了产品种类变化对能源绩效参数的影响。以上节能量计算方法是针对节能项目中期或结题的离线评估,并不能及时调整不合理的技术参数。然而,有效利用电能替代项目调试期的少量量测数据,进行快速准确节能量估计,及时调整电能替代技术参数,可以更为有效地推进电能替代技术应用。
节能量估计的实现需要搭建项目能耗模型,而能耗模型的搭建可通过回归算法进行拟合。在实际应用中,进行在线节能量评估可能会遇到样本量很少或标注样本量很少的问题。小样本学习目标是从少量样本中学习到解决问题的方法,是目前机器学习的关注热点之一,其中,迁移学习是一大解决思路[14]。文献[15]针对建筑能耗数据成因复杂、独立同分布性弱、目标域样本不足的现状,提出了基于迁移深度强化学习的建筑能耗预测方法,对建筑能耗之间的深度特征进行提取,最大限度利用其他建筑能耗的数据信息,从而提高目标建筑能耗预测性能。文献[16]为解决智能变电站电力设备图像数据集样本较少、场景复杂且电力设备相似度较高的问题,提出了一种利用单阶段多框检测器的智能变电站电力设备图像目标检测算法,将预训练模型进行层迁移,根据不同小样本数据集的特点加载不同的模型参数和权重,选择不同的卷积层,微调卷积神经网络,从而增强电力设备部件检测精度、降低平均漏检度和平均误检度。
综上所述,为充分利用电能替代项目调试期少量样本数据,本文采用基于迁移学习的回归算法以提高调试阶段的小样本回归算法精度;然后基于迁移学习的回归算法,提出一种通用的单位节能量在线估计方法,可针对不同技术领域的电能替代项目,在电能替代调试期进行节能量的精准估计,从而设置合理的电能替代技术参数。
1 基于迁移学习的回归算法
传统的回归算法需要消耗大量的样本数据,而基于样本迁移的回归算法仅需要少量的目标域样本,借助源域大量样本信息,将源域中学到的知识、特征迁移到目标域,即可构建目标域模型。其中,源域和目标域应存在一定的关联,源域和目标域关联性越强,迁移学习的效果越好。TrAdaBoost.R2算法作为一种基于样本迁移的回归算法[17],其原理可描述如下。
TrAdaBoost.R2算法将2个数据集样本、样本权重作为输入,利用传统的回归算法,多次迭代调整样本权重,并采取加权机制对迭代回归的结果进行叠加,得到最终的回归值。算法涉及的数据集有:源域数据集Dsource、目标域数据集Dtarget、总样本数据集D(将源域数据集、目标域数据集合并得到的数据集)。针对源域数据集、目标域数据集的样本,算法采取不同的权重更新策略以达到源域知识、特征的迁移,即降低与目标域样本相似的源域样本的权重,增加与源域样本相似的目标域样本的权重。TrAdaBoost.R2算法的流程如图1所示。
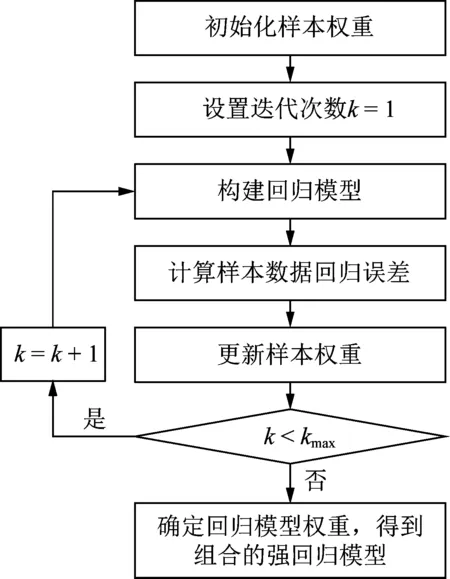
图1 TrAdaBoost.R2算法流程Fig.1 Flowchart of TrAdaBoost.R2 algorithm
1)初始化样本权重。
数据集D的样本数为m+n。其中,前m个样本为源域样本,后n个样本为目标域样本。对样本权重进行初始赋值,计算公式如式(1)所示:
(1)
式中:ω0,i为第i个样本的初始权重。
2)设置迭代器。
设置迭代次数k=1。
3)构建回归模型。
将数据集D、样本权重作为输入,利用简单的弱回归算法,进行训练,获得回归模型。典型的弱回归算法有线性回归、岭回归、决策树回归、支持向量机回归、神经网络回归等。
4)计算样本数据的回归误差。
计算步骤3)得到的回归模型相对于目标源数据集Dtarget的预测误差,计算公式如式(2)所示:
(2)
式中:εk为第k次迭代过程中回归模型的预测误差;ωk,i为第k次迭代过程中第i个样本的权重;yi为目标源数据集Dtarget中样本i的因变量;xi为目标源数据集Dtarget中样本i的自变量;Fk(·)为第k次迭代过程中获得的回归模型;Fk(xi)为通过Fk(·)得到的预测值。
5)更新样本权重。
定义权重改变系数βk,i,如式(3)所示:
(3)
式中:kmax为最大迭代次数。
然后,利用权重改变系数βk,i,得到更新后的权重ωk,i,如式(4)所示。
(4)
进一步地,通过对ωk,i进行归一化处理,使得样本权重满足式(5)要求。
(5)
6)判断是否达到最大迭代次数。
判断是否达到最大迭代次数kmax,如果达到最大迭代次数,进入步骤7);反之,返回步骤3)。
7)确定回归模型权重,得到组合的强回归模型。
利用第kmax/2~kmax次迭代训练得到的回归模型进行组合,线性加权得到最终的强回归模型,每次迭代的回归模型的权重计算公式如式(6)所示。
(6)
式中:βk为第k次迭代中的目标域权重改变系数。
2 基于迁移学习的单位节能量在线估计模型
2.1 节能量计算原理
能源消耗模型可基于物理学、统计学模型或其他模型建立,能耗模型的通用数学模型如式(7)所示:
E=f(x1,x2,…,xj)
(7)
式中:E为能源消耗;f(·)为能耗模型函数,其中x1,x2, …,xj为影响能源消耗的相关变量。能耗模型可依据物理关系、经验公式或回归算法等方法建立。本文采取回归算法建立能耗模型。
节能量是指一段时间内满足同等需求或达到相同目的的条件下的能源消费减少量,节能量相关参数关系如图2所示。基期为节能措施实施前的时间段,报告期为节能措施实施后的时间段。通过确定用能边界、能源基准、基期和报告期,并对基期和报告期能源消耗进行归一化,归一化后的基期能耗和报告期能耗之差即为采取节能措施后的节能量[18]。
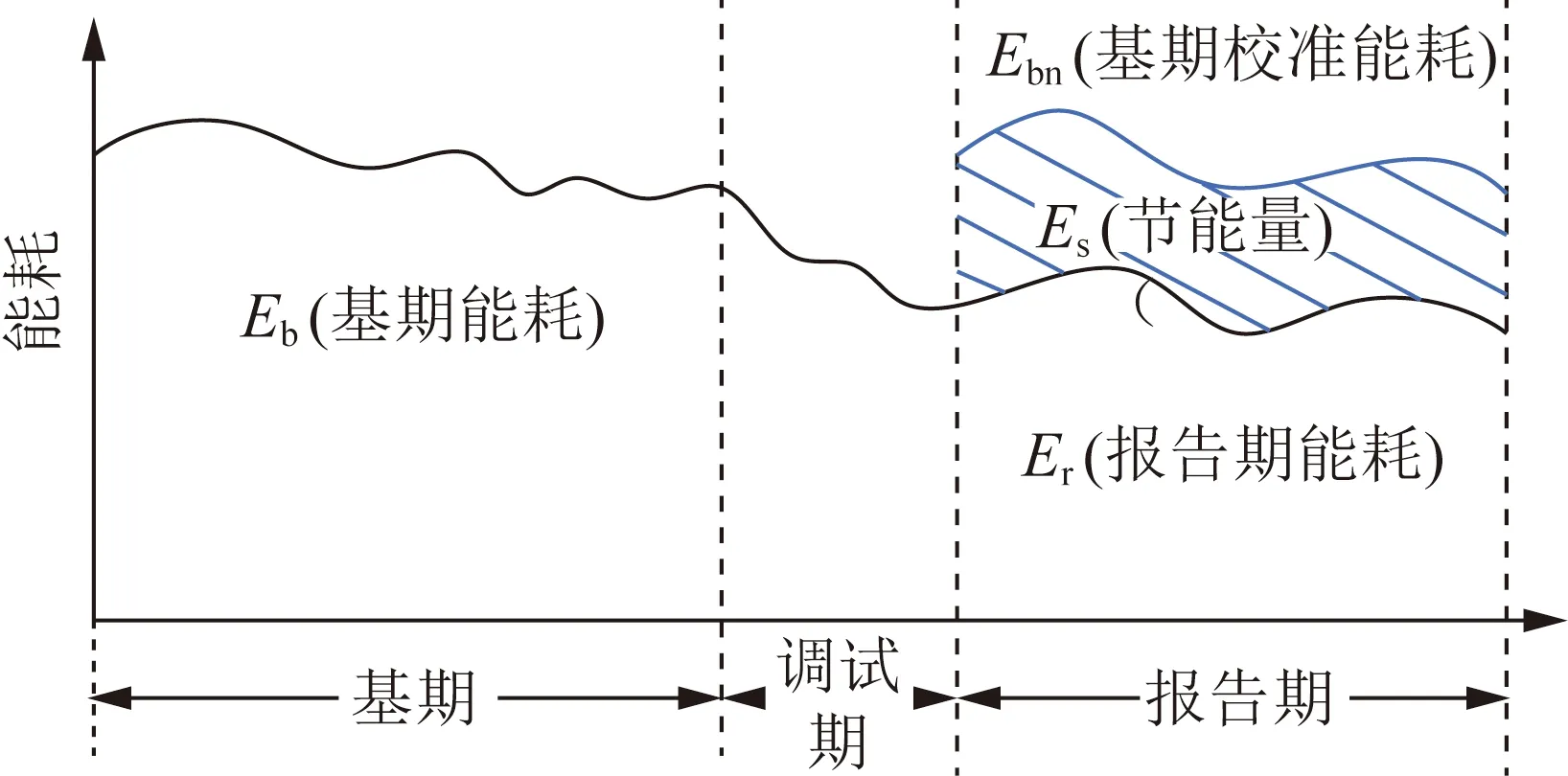
图2 节能量相关参数示意图Fig.2 Schematic diagram of energy-saving related parameters
归一化方法可分为后推校准法、前推校准法和参考条件校准法。本文选择参考条件校准法进行计算,如式(8)所示:
Esave=Ebn-Ern
(8)
式中:Esave为节能量;Ebn为基期校准能耗;Ern为报告期校准能耗。利用基准期能耗模型和报告期能耗模型,在统一参考条件下,即可获得节能措施实施后的节能量。
2.2 单位节能量在线估计原理
如图2所示,电能替代项目运行按时间划分可分为基期、调试期和报告期。通常利用基期数据、报告期数据对电能替代项目进行节能量计算,未能有效利用调试期数据。针对调试期能耗数据,可以对电能替代项目进行节能量估计,对不同工况下的节能量进行预估,从而对电能替代项目做进一步调试,获得合理的电能替代项目技术参数设置。因此,定义单位节能量为一定工况下,相同单位产量下相对于基期能耗的减少量。本节采取基期数据、调试期数据作为输入值,考虑调试期数据样本数量不足,构建基于迁移学习的电能替代单位节能量在线估计模型,具体建模流程如图3所示。
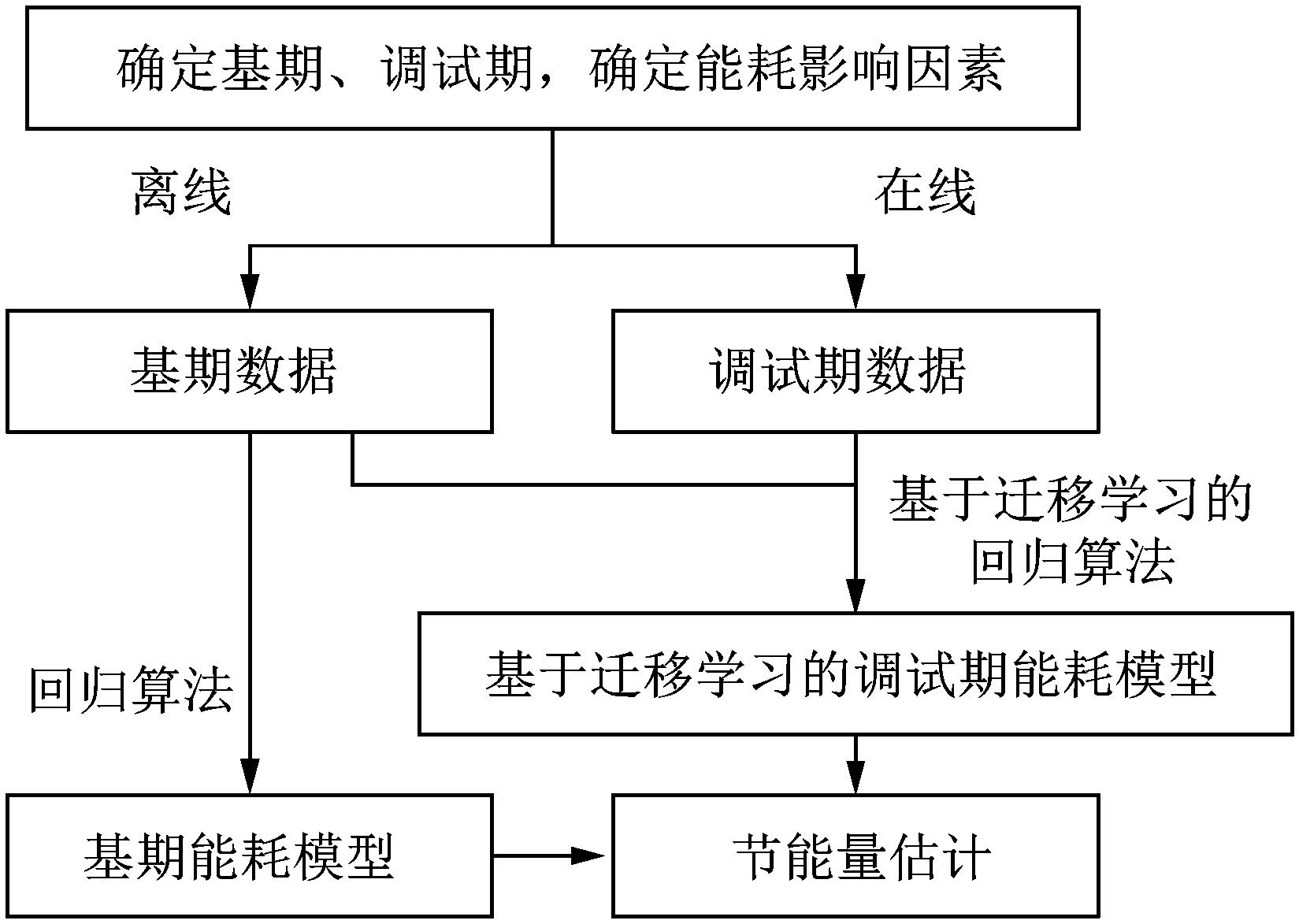
图3 单位节能量在线估计模型流程Fig.3 Flowchart of online unit energy-saving estimation model
1)数据采集。
确定电能替代项目基期、调试期,并确定能耗影响因素,对基期数据、调试期数据进行采集。其中,基期数据为离线数据,样本容量大;调试期数据为在线数据,进行实时采集,样本容量小。
2)建立基期能耗模型。
利用基期数据,采用回归算法建立电能替代项目基期能耗模型。
3)建立基于迁移学习的调试期能耗模型。
利用基期数据和调试期数据,采用基于迁移学习的回归算法,调整基期样本权重和调试期样本权重,建立调试期能耗模型。
4)单位节能量估计。
确定影响因素取值,利用基期能耗模型获得确定影响因素下的能源消耗量,利用调试期能耗模型获得参考影响因素下能源消耗量,将两者相减求得此节能措施下的调试期单位节能量。
3 算例分析
3.1 样本数据描述
本文针对干燥领域的电能替代进行案例分析,干燥箱能耗模型参照文献[19-20],计算公式如式(9)所示,详细推导见附录A。
(9)
式中:A为干燥箱托盘面积;v为空气流速;ρa为干燥箱入口空气密度;Ca为干燥箱入口空气比热容;T为温度;Tabs为烘箱入口温度;M0为烘烤物料初始干基含水率;Mt为t时刻物料干基含水量;a、b为温度拟合系数,与烘烤温度有关。在本案例中,入口空气流速v、入口空气温度Tabs、烘烤温度T、烘烤物料初始干基含水率M0为总能耗的主要影响因素。确定3种工况(烘烤温度分别为340 K、350 K和360 K),随机生成正态分布的样本数据,利用干燥箱能耗模型计算干燥箱烘干物品所需热能。样本信息如图4、5所示,其中,四分位差(inter quartile range,IQR)为样本数据中高四分位数与低四分位数之差,1.5IQR范围内数据为非异常数据。1.5IQR范围外的样本数据为异常值,服从标准正态分布的样本中只有极少数为异常值。如图4所示,本案例干燥箱的入口空气速度样本均值为1.5 m/s,入口空气温度为300 K,烘烤物品初始湿度样本均值为80%。根据能耗影响因素计算获取热能需求,由图5可知,3种典型工况下,热能需求分别约为0.47、0.54和0.59 m2·kJ。
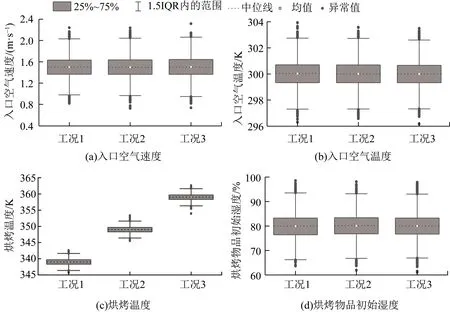
图4 样本能耗影响因素分布信息Fig.4 Sample distribution information of factors affecting energy consumption
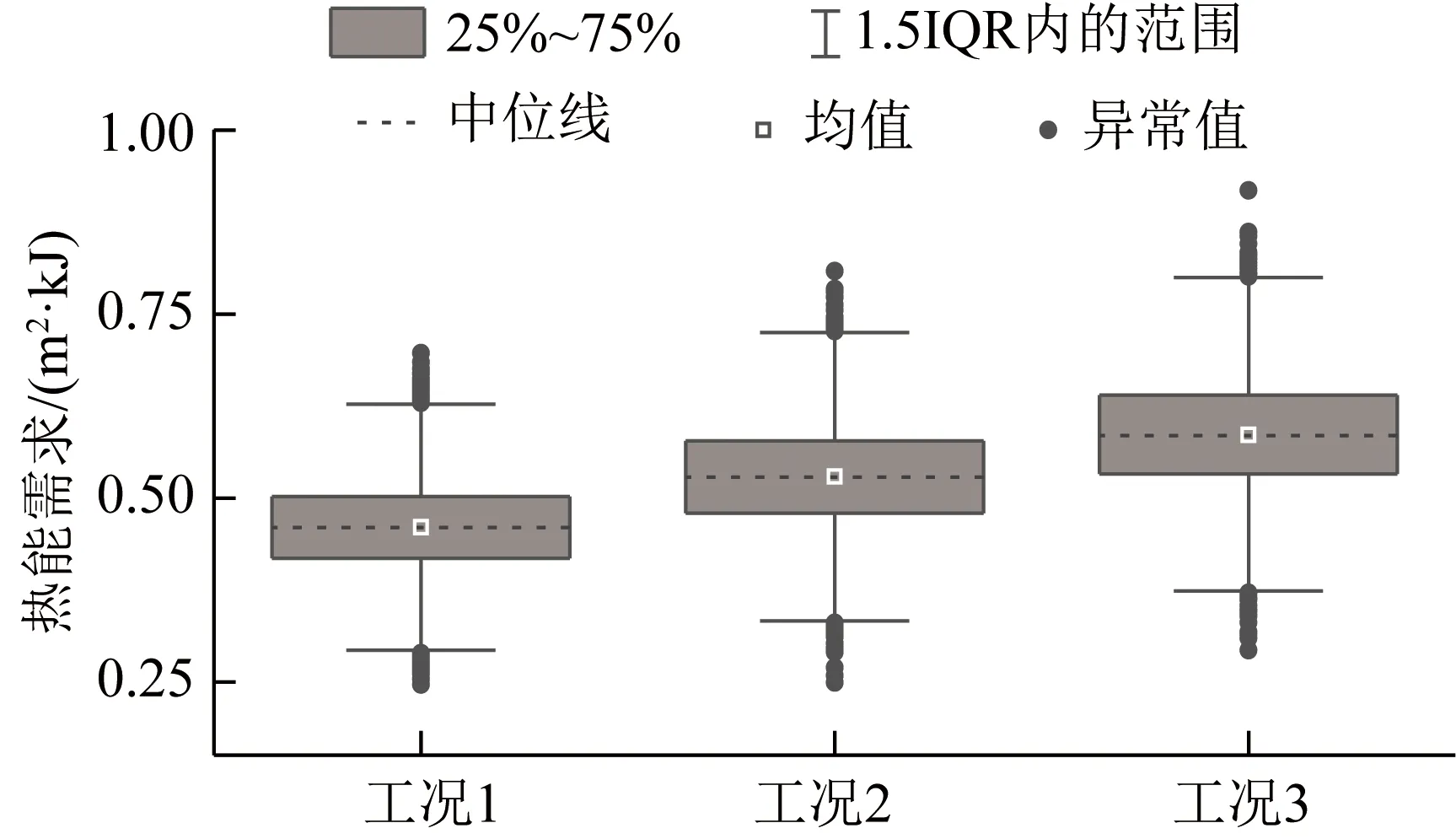
图5 样本热能需求分布信息Fig.5 Sample distribution information of thermal demand
3.2 估计结果与算法误差分析
3.2.1 单位节能量估计结果
设置干燥箱电能替代场景,基期样本采取工况2样本,且采取燃煤锅炉作为干燥机的热源;调试期样本采取工况1样本,且采取电锅炉作为干燥机的热源。典型燃煤锅炉的热效率为80%,电锅炉的电效率为90%。取参考影响因素为入口空气速度1.5 m/s,入口空气温度300 K,烘烤温度340 K,烘烤物品初始湿度80%。根据干燥箱能耗模型可知,理论上,干燥箱所需热量为0.469 0 m2·kJ,燃煤锅炉需消耗煤能量为0.586 3 m2·kJ,电锅炉需消耗电能量为0.521 1 m2·kJ,进行电能替代后单位节能量为0.065 1 m2·kJ。
当基期样本数量为500,调试期样本数量为20时,对其进行单位节能量估计。采取随机抽样的方法进行采样,获取样本数据。选取神经网络回归算法作为本案例的弱回归算法,该神经网络设置为双层前馈神经网络,隐含层网络的激励函数设置为tansig函数,隐含层节点数设置为5,输出层网络的激励函数设置为purlin函数,采取动量批梯度下降方法训练神经网络,学习率设置为0.01,动量因子设置为0.9。设置基于迁移学习的回归算法的迭代次数为50。针对相同的采样样本,多次单位节能量估计结果如表1所示。其中,本文所涉及的预测误差均为绝对百分比误差。由表1可知,基期样本数目为500、调试期样本数为20时,本文所提方法燃煤锅炉能耗模型预测误差和电锅炉能耗模型预测误差均在0.6%以内,单位节能量预测误差在3.2%以内,可达到较高的预测精度水平。
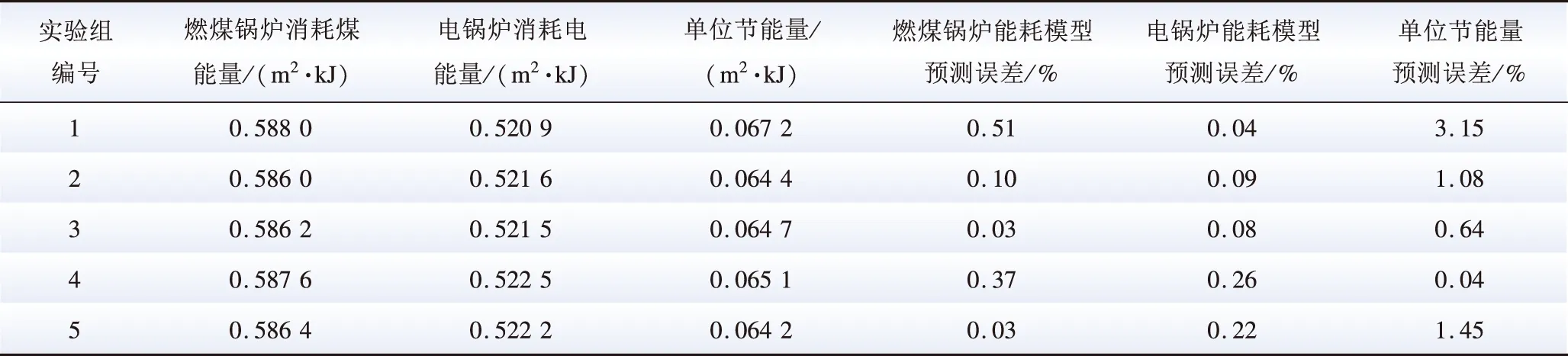
表1 干燥箱电能替代场景单位节能量估计结果Table 1 Energy-saving estimation results of electric energy substitution in drying oven
3.2.2 单位节能量在线估计算法误差分析
为了研究算法误差和样本数据的关系,首先对弱回归器进行误差分析。本实验中,神经网络训练数据的输入为工况1、工况2、工况3的影响因素,训练数据的输出为对应的干燥箱所需热量,神经网络设置与上文相同。经过多次独立重复试验,获得预测误差随样本增加的取值,如图6所示。可知,随着样本个数增加,预测误差急剧降低,直至样本个数达到50后,预测误差降低幅度变缓。由于本案例选择的干燥箱模型复杂度不高,传统神经网络的拟合效果较佳,样本数目为40时已达到一定的预测精度。实际应用中,由于各种非线性因素影响,在同等样本数目下,预测误差可能会更大。
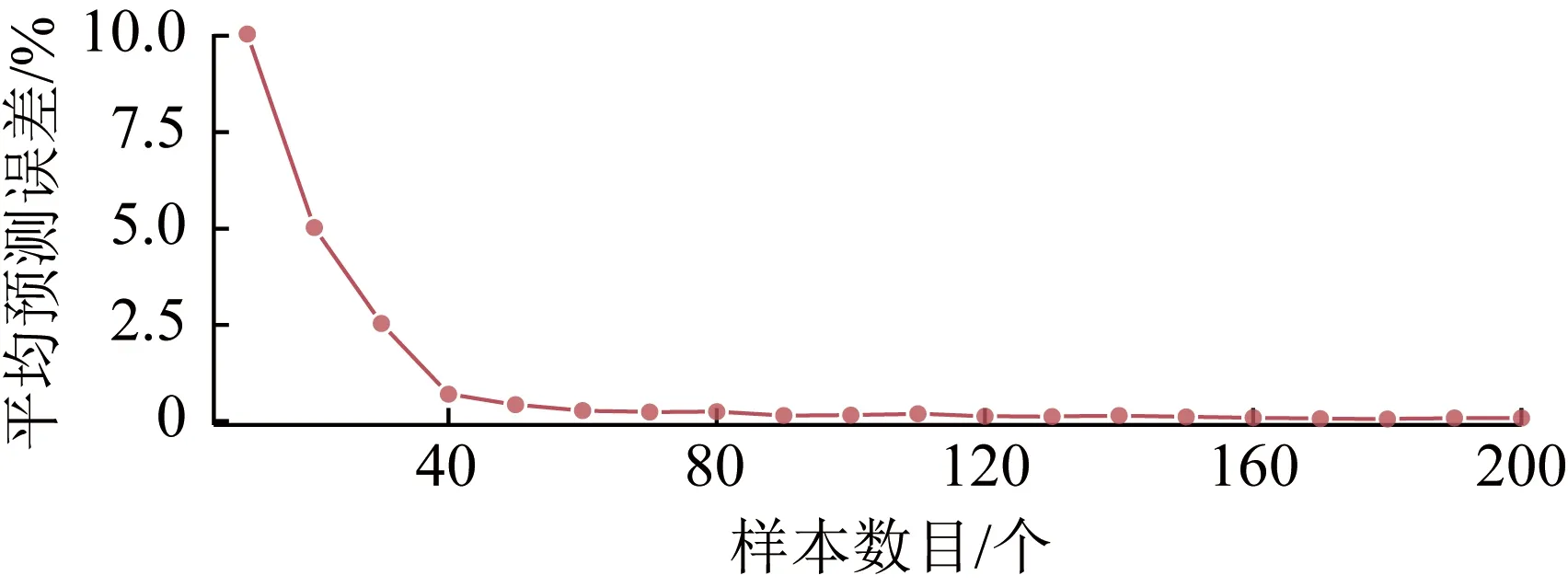
图6 样本数目与神经网络预测误差关系Fig.6 Relationship between the number of samples and the prediction error of neural network
此外,所提算法通过多次迭代改变基期、调试期样本权重,迭代次数设置也会大大影响算法精度。设置基期样本数目为100,调试期样本数目为20,神经网络设置同上文,通过多次独立重复试验,得到迭代次数与算法预测误差关系,如图7所示。可知,随迭代次数增加,平均预测误差降低,当达到一定迭代次数后,平均预测误差呈波动状。在本案例中,设置迭代次数为50,即可达到较佳的预测精度。因此,针对本案例应用的干燥箱模型,本文讨论调试期样本数目小于50时的情况下所提算法的精确度。
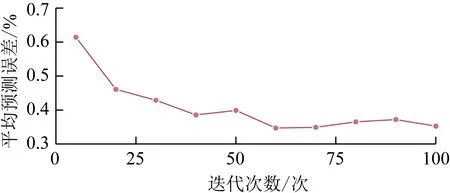
图7 迭代次数与算法预测误差关系Fig.7 Relationship between the number of iterations and the algorithm prediction error
本文考虑以下4种对比方案算法来验证本文算法:方案1,仅利用调试期小样本数据作为输入,训练神经网络;方案2,仅利用基期大样本数据作为输入,训练神经网络;方案3,利用调试期小样本数据、基期大样本数据作为输入,但不调整样本权重;方案4,利用调试期小样本数据、基期大样本数据作为输入,同时迭代调整样本权重,即本文所提算法。
进一步地,本文考虑了3种样本数据组合方式,分析基期样本数据、调试期样本数据的相关性对预测误差的影响。样本组合方式设置如下:组合1,基期数据、调试期数据的自变量均从工况1、工况2和工况3中随机采样,基期数据、调试期数据的因变量取对应的电锅炉需消耗的电能量,在本样本组合下,源域、目标域自变量分布相关性大,且自变量-因变量模型相同;组合2,基期数据自变量从工况1中随机采样,调试期数据的自变量从工况2中随机采样,基期数据、调试期数据的因变量取对应的电锅炉需消耗的电能量,在本样本组合下,源域、目标域自变量分布相关性较小,但自变量-因变量模型相同;组合3,基期数据自变量从工况2中随机采样,其因变量取相对应的燃煤锅炉需消耗的煤能量,调试期数据自变量从工况1中随机采样,其因变量取相对应的电锅炉需消耗的电能量,在本样本组合下,源域、目标域自变量分布不同,且自变量-因变量模型不同。
针对上文提到的4种对比方案算法、3种样本组合方式,进行多次独立重复试验,神经网络设置、迭代器设置同上,仿真结果如图8—10所示。可知,所提基于迁移学习的回归算法在不同样本组合方式、不同样本数设置条件下,均具有良好的预测效果。此外,不同样本组合下,基于迁移学习的回归算法平均预测误差受样本数目的影响不同。随调试期样本数目增加,样本组合1下的平均预测误差变化相对小,样本组合2、3下的平均预测误差变化相对大,原因是样本组合1下基期能耗模型和调试期能耗模型相似度大,而样本组合2和样本组合3下基期能耗模型和调试期能耗模型相似度小。基期和调试期模型相似度越大,获得一定预测精度所需要的调试期样本数目越少。随基期样本数据增加,方案3、4算法的平均预测误差略有降低,在基期样本数目足够大的情况下,增加基期样本数目对算法准确度的影响不大。
由图8可知,由于样本组合1中调试期样本、基期样本分布相似、能耗模型相同,基期样本数据量足够,因此,方案2、方案3和方案4的平均预测误差极小,且相差不大,甚至出现当调试期样本数为10时,方案3的平均预测误差小于方案4的平均预测误差,即本文所提的基于迁移学习的回归算法。这是由于基期样本数目远大于调试期样本,基期样本、调试期样本分布有一定差异,出现了一定量的负迁移。基期样本的学习对调试期样本的学习产生了消极影响和不良作用。
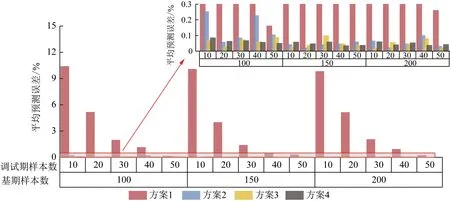
图8 样本组合1下算法预测误差对比图Fig.8 Comparison chart of algorithm prediction error on sample combination 1
由图9可知,由于样本组合方式2所采取的基期能耗模型和调试期能耗模型相同,当调试期样本数目增加至50时,仅通过调试期样本即可达到可观的预测精度。然而,本文所提算法的预测精度在大多场景中,具有最低的平均预测误差,有效利用了基期样本数据。
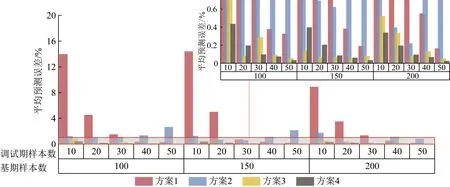
图9 样本组合2下算法预测误差对比图Fig.9 Comparison chart of algorithm prediction error on sample combination 2
由图10可知,即使在电能替代影响因素分布不同、能耗模型不同的情况下,仍然可以通过基于迁移学习的回归算法进行基期样本数据学习,获得高精度的能耗预测模型。由于样本组合方式3所采取的基期能耗模型和调试期能耗模型不同,因此,方案2得到的平均预测误差最大。
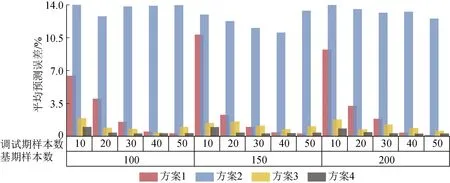
图10 样本组合3下算法预测误差对比图Fig.10 Comparison chart of algorithm prediction error on sample combination 3
4 结 论
本文基于迁移学习通过权值更新策略改变基期、调试期样本权值,提出了电能替代单位节能量在线估计模型。本文充分利用了基期大样本信息和调试期小样本信息,从而建立了高精度调试期能耗模型。本文将提出的方法应用于干燥箱单位节能量估计案例中,针对不同工况进行仿真验证,实验效果验证了方法的有效性。由于本文研究的干燥箱数学模型相对简单,所以在样本数据量为50的时候,回归模型的精度已经很高。但实际应用中,由于各种非线性因素,回归模型精度可能会降低。综上,本文所提方法可在电能替代调试阶段调整不合理的项目参数,对项目能耗做及时反馈,获得合理的电能替代项目技术参数,有利于电能替代项目的推广。
