基于极限学习机的有源配电网多场景静态电压安全分析

撖晨宇，胥鹏，朱红，刘少君，王蓓蓓

(1.东南大学电气工程学院，南京市 210096；2.国网江苏省电力有限公司南京供电分公司，南京市210000)

0 引 言

随着全球环境污染及能源危机问题的加重，分布式可再生能源(distributed renewable generation，DRG)的并网逐渐成为清洁能源的主流发展方向。美国加州通过了新建住宅必须安装太阳能电池板的法案，当地光伏装机已达3 100万kW，占电源总容量的30%；我国浙江省分布式可再生能源的接入规模2018年已达1 500万kW，占全省装机总容量的10%[1]。分布式可再生能源具有安装灵活、成本低、降低终端网络依存度的优势，具有良好的市场前景[2-3]，但分布式可再生能源的接入增加了地区配电网的不确定性，电压越限等配电网风险也随之日益严重[4-9]，配电网也面临着供电质量下降、网损提高及大规模停电的巨大危机[10]。考虑DRG接入的配电网安全分析主要有以下几个特点：其一，配电网拓扑的支路数量比大电网多得多，进行静态电压安全分析要做的潮流计算由于有功和无功无法解耦，复杂性较高；其二，现存的大量分布式电源以单相形式进行并网[11]，基于三相潮流对配电网进行安全分析更加符合实际；其三，考虑DRG接入的有源配电网相较于传统配电网来说， DRG输出的不确定性导致静态电压安全分析的场景数显著增加。因此，若采用传统的配电网三相潮流计算方法电流注入法[12]及序分量法[13]进行安全分析，计算量相对较大，庞大的场景数目下，需要消耗大量的时间，在实际工程应用中缺乏效率的保障。另一方面，随着近年人工智能技术的发展及硬件技术的成熟，利用机器学习模型在有限数据的基础上进行快速潮流计算[14-15]，从而快速完成配电网络的安全分析已经成为学者们广泛关注的一个研究课题。

目前，相关的研究主要集中在配电网的电压安全分析及潮流计算两个方面。配电网电压安全分析方面，文献[16-17]设计了主动配电网静态电压安全分析的评估指标，基于半不变量法对配电网的安全性给出了评估。半不变量法为了计算效率采取了一系列近似与假设，可能导致计算结果具有较大的误差，且缺乏对单相接入DRG的考虑。机器学习方法在安全分析中也得到了较为广泛的应用[18-20]，但普遍缺乏对分布式能源及三相不平衡度的考虑，且卷积神经网络[19]、深度神经网络[20]训练中均需要经过大量的反向传播，需要较长的训练时间。三相潮流的计算方面，文献[21-24]提出了多种三相潮流计算方法，但仍然受到三相潮流计算效率、变量要求、收敛性能等限制，用于分析DRG接入的有源配电网过电压、三相不平衡等安全问题时存在不足。

考虑到DRG变化带来的有源配电网运行场景数目的增长对安全分析中潮流计算的效率提出了更高的要求，本文从极限学习机(extreme learning machine，ELM)能够有效逼近连续函数、具有高效训练效率的特性出发，针对配电网络拓扑结构、新能源安装可能发生变化的特点，采用极限学习机模型实现电压越限及三相电压不平衡程度的快速计算。基于构建的模型对有源配电网静态安全状态进行辨识，根据分析结果给出新能源波动下容易出现电压越限及不平衡问题的脆弱节点，提出必要的改进措施。

由于采用配电网终端用采数据进行数据驱动模型的训练，本文提出的模型在具备接近传统模型的准确性的同时，克服了传统模型收敛性能的问题，与深度神经网络、卷积神经网络等模型相比也具有更高的训练效率。本文的研究工作将有助于指导分布式风光发电设备的安装，引导配电网运营商加强运营及技改工作，提高供电可靠性。

1 基于极限学习机的三相潮流计算模型

本文选择GridLAB-D[25]时序仿真软件生成训练模型所需的数据集，以替代实际应用中的用户端采集数据。

极限学习机是一种单隐含层的前馈神经网络[26-27]，具有自主学习训练速度快、保证全局最优解的特点。建立13节点配电网络及极限学习机模型进行三相潮流计算，其输入输出结构如图1所示。

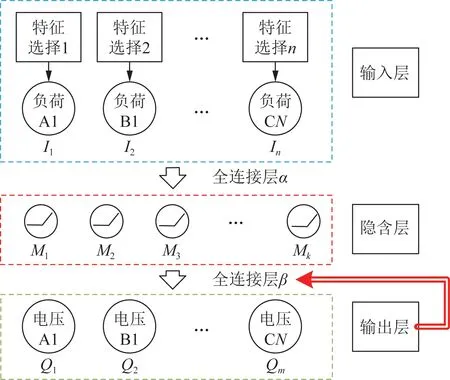
图1 极限学习机结构Fig.1 Structure of ELM

ELM模型的主要参数包括隐含层节点数目及节点激活函数，对于节点激活函数为g(·)的ELM模型，输出节点的输出结果如式(1)所示：

(1)

式中：T表示模型的输出结果；i表示隐含层节点编号；ωi、bi表示输入神经元与隐含层节点i之间的连接权值及偏置；xi表示连接到隐含节点i的所有输入构成的输入矩阵；g(·)表示激活函数；βi表示第i个隐含层节点与输出节点连接权值；β表示隐含层与输出节点连接权值构成的矩阵；H表示隐含层输出矩阵，其显式表达如式(2)所示：

(2)

式中：xj表示第j个输入神经元输入特征。则ELM模型的训练过程可以由式(3)来表示：

(3)

式中：a表示训练数据集中的样本编号；ya表示样本a对应的模型输出结果。

隐含层与输出层的连接参数矩阵β可以对式(4)求解得到：

β=H+TT

(4)

式中：H+为隐含层输出矩阵H的广义逆；TT为模型输出的转置。

本文采用GridLAB-D提供的美国盐湖城2002年8 760 h内的光照数据计算DRG的出力上下限。为了方便工程研究，认为DRG的出力只跟光照强度有关，其计算方式如式(5)所示[28]：

(5)

式中：PPV表示DRG实际输出功率；Gac表示当前时刻光照强度；Pstc表示光伏最大测试功率；Gstc表示标准测试条件下的光照强度，本文中取GridLAB-D软件所提供的光照数据均值。

为消除奇异样本对模型产生的影响。本文选择最大最小归一化方法对数据进行预处理，并按照时序以9∶1比例划分训练数据及验证数据，采用十折交叉验证的方法提升模型的泛化能力。

2 配电网静态电压安全分析挖掘辨识

2.1 场景设计

本文在处理DRG出力不确定性时，主要根据DRG数量以及DRG波动程度的不同，生成不同的随机场景，统计分析多场景下配电网各节点的安全状态，来实现不确定性情况下的安全分析。以安装2个DRG为例，每个DRG都会因外界条件变化而产生出力的上下限，根据上下限的差值可以生成该DRG出力的多种情况，通过组合不同的出力情况可生成不确定性下的随机场景进行分析，具体步骤如下：

1)确定系统中接入DRG的数目。实际中可根据系统规划要求确定配电系统中可用于安装DRG的节点集合。

2)选择DRG接入位置。从可用于安装DRG的节点集合中选取n个节点用于接入DRG。

3)确定各节点DRG功率。对n个节点的DRG接入功率按照一定的间隔依次增加，本文中间隔S取2 kW，以此为依据生成DRG出力递增序列P。

4)模拟多个场景。重复步骤3)，重复抽样得到DRG的接入功率，计算不同功率场景下的节点电压幅值、三相电压不平衡度，记录并保存各个场景下的计算结果。

2.2 指标设计

随着DRG渗透率的不断增长，配电网的不确定性不断增加，配电网的电压越限风险成为了配电网主要风险之一。另外，大量分布式电源以单相形式进行并网[11]，将带来节点三相电压不平衡问题。因此，本文对于节点安全性指标的设计主要考虑电压越限及电压不平衡度两个方面，指标值越高，电压越限及三相电压不平衡的潜在风险越高，节点安全性越低；指标值越低，电压越限及三相电压不平衡的潜在风险越低，节点安全性越高。其计算公式如式(6)所示：

(6)

式中：S1代表2.1节中生成的所有不确定性负荷场景；ωs,i代表场景s下节点i的电压越限状况，其计算方式如式(7)所示[29]；μs,i代表场景s下节点i的三相电压不平衡度，计算方式如式(8)所示[30]；K为场景个数比例系数，本文算例中取10 000；N表示配电网具有的节点数目。

(7)

式中：Vi表示节点i的三相潮流计算结果,i=1,2,…,N；Vmax及Vmin分别表示节点i电压幅值的上限与下限。

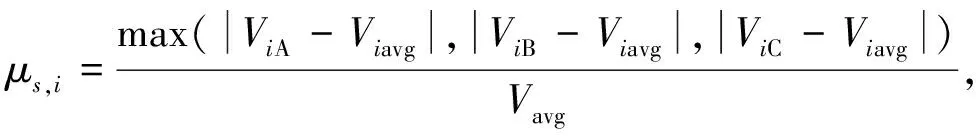
(8)

式中：Viavg表示节点i三相电压的平均值；ViA,ViB,ViC表示节点的三相电压幅值。

2.3 安全分析流程

根据2.1节及2.2节对不确定性场景及分析指标的描述，本文提出的基于极限学习机的有源配电网静态电压安全分析流程如下：

1)基于现有电网潮流信息生成训练数据集，完成ELM模型的训练。

2)根据有源配电网中实际DRG安装的数量，按照式(5)及GridLAB-D提供的光照数据，计算DRG出力的上下界限，对每一个DRG在其出力上下限之间进行m次插值，对n个DRG的出力进行离散化。

3)对离散化的DRG出力结果进行随机负荷情景的生成。

4)基于步骤1)中的ELM潮流计算模型，根据式(6)—(8)计算当前场景负荷下各个节点综合安全性。

本文提出的配电网安全分析流程如图2所示。图中：C表示ELM模型的验证集误差，ε表示误差阈值，Di为节点i的出力，S表示场景生成过程中节点出力调节的步长，Dall表示所有节点的出力，Dceil表示场景生成过程中的节点出力上限。

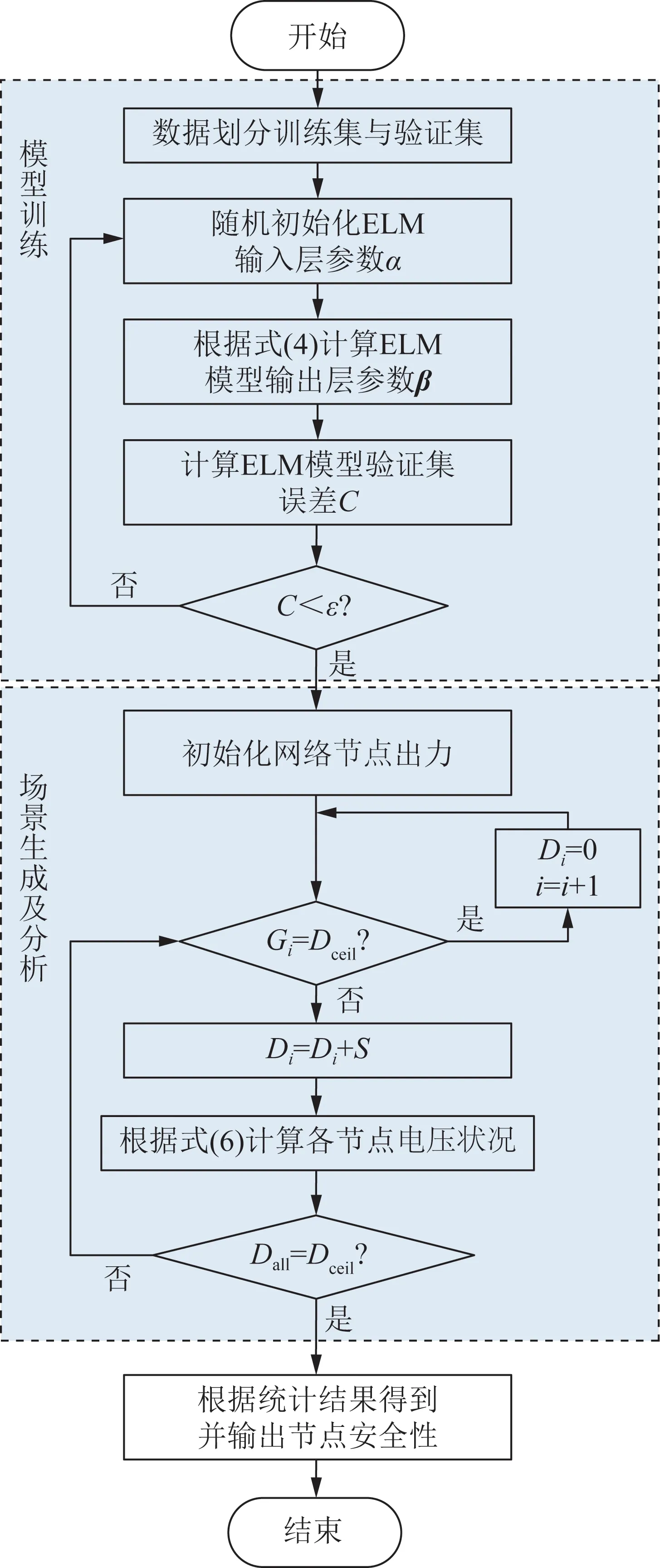
图2 配电网安全分析流程Fig.2 Process of distribution network safety analysis

3 算例分析

本文设计算例对所提模型的有效性进行论证，实验环境为AMD2200G处理器，8 GB内存，编程语言选择Python3.7，分别设计安全分析实验及模型性能对照实验。本文实验中选取了IEEE 13节点的配电网[31]。

3.1 潮流计算模型分析

3.1.1 模型选择对计算结果的影响分析

本节对3种不同的潮流计算方法从时间、准确性两方面进行对比。除本文模型外其他2种计算方法如下：

1)GridLAB-D时序仿真。通过GridLAB-D建立仿真网络，通过前推回代法实现网络三相潮流的计算。

2)BP神经网络模型。选取的神经网络为深度神经网络模型，根据文献[32]中的网络结构，该BP神经网络具有3层隐层，分别具有100、500、1 000个神经元，激活函数选择Relu函数。输入数据为配电网络所有节点的三相负荷，输出数据为配电网所有节点的三相电压。

对上述2种模型及极限学习机模型从精确度、运行时间及训练时间3方面进行性能比较，其中，BP神经网络模型与极限学习机模型的精确度比较通过模型在测试集上的均方根误差(root mean square error，RMSE)来表示，其计算方式如式(9)所示。

(9)

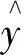
不同模型的性能比较结果如表1所示。

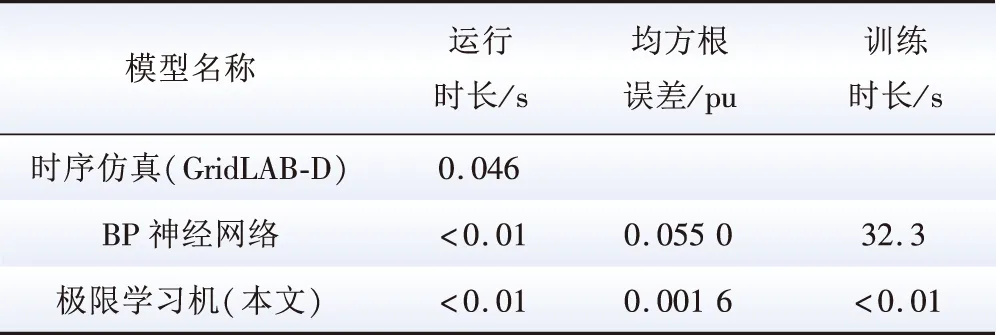
表1 不同模型的性能比较Table 1 Comparison among different Models

表1显示，利用GridLAB-D直接进行三相潮流的计算虽然可以保证计算结果的准确性，但由于需要考虑有功无功解耦、分解等问题，进行大量的矩阵运算，导致时序仿真需要的时间较长，达到0.046 s。相反，BP神经网络及极限学习机在计算时间上具有明显的优势，在上述两种机器学习模型中，极限学习机在测试集上平均误差比神经网络的平均误差更低，说明极限学习机模型在三相潮流计算问题上比传统的BP神经网络具有更强的泛化能力；另一方面，BP神经网络的训练时长(32.3 s)明显高于极限学习机(小于0.01 s)。在实际应用中，当配电网网络拓扑变化时，极限学习机能够更加快速地实现重新训练，从而保障潮流计算的结果不会因配电网结构的改变产生更大的误差。

3.1.2 ELM参数对计算结果的影响分析

在极限学习机模型中，隐层的数目将会对结果产生较大的影响，不合理的数目设置将会导致欠拟合或过拟合问题[12]，不同参数的极限学习机泛化能力如表2所示。

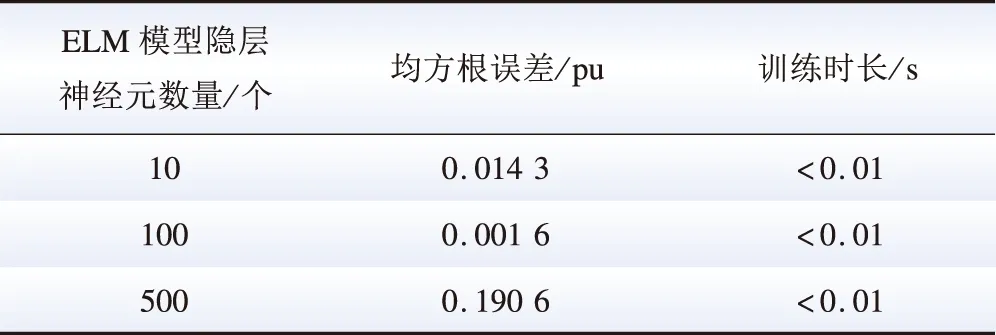
表2 不同参数的极限学习机性能比较Table 2 Comparison of ELMs with different parameters

表2显示，当ELM的隐层数目选择10与100时结果相差不大，但在隐层数目达到500时误差远远超过其他模型，推断此时出现了严重的过拟合；隐层个数为10时均方根误差略大于隐层个数为100的模型，可能出现了轻微的欠拟合。因此选择100为最终的模型参数，此时极限学习机在测试集上的均方根误差为0.001 6。

3.1.3 不同规模DRG对计算结果的影响分析

在采用随机场景分析的方法进行静态电压安全分析时， DRG规模的变化会导致场景的构成出现较大幅度的变化，因此本节在图3所示的IEEE 13节点配电网中，对不同规模、不同位置DRG接入的情景进行时间效率上的比较，结果如表3所示。

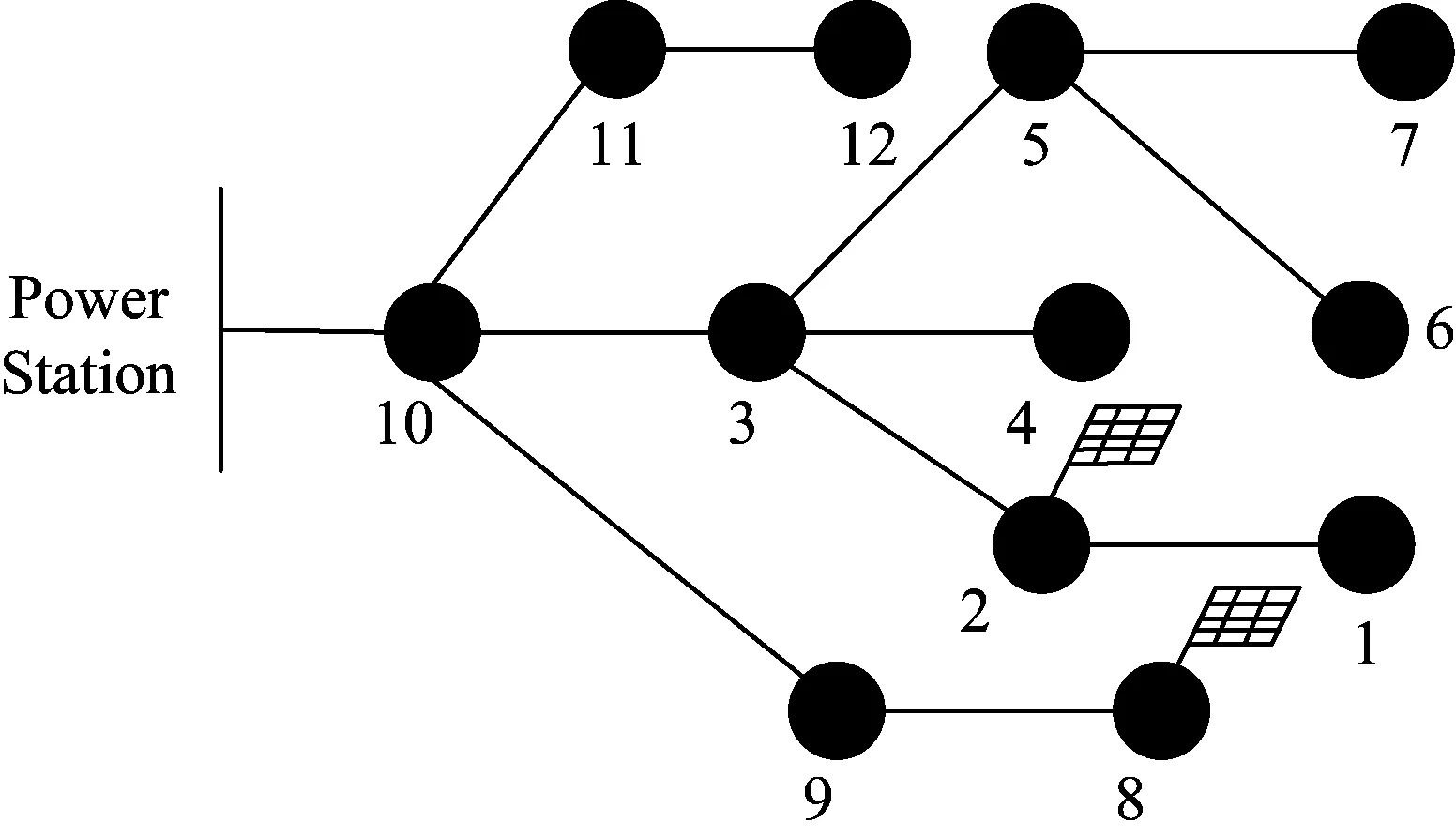
图3 IEEE 13节点网络示意图Fig.3 IEEE 13-node system

由表3可知，随着DRG接入规模的扩大， GridLAB-D计算所需要的时间显著增加；当DRG接入点位于2、4、8、9节点时，BP神经网络给出了错误的分析结果，而ELM极限学习机结果与仿真一致，推测BP网络在训练过程中出现了局部最小值。该缺陷是由模型的训练方式决定的。

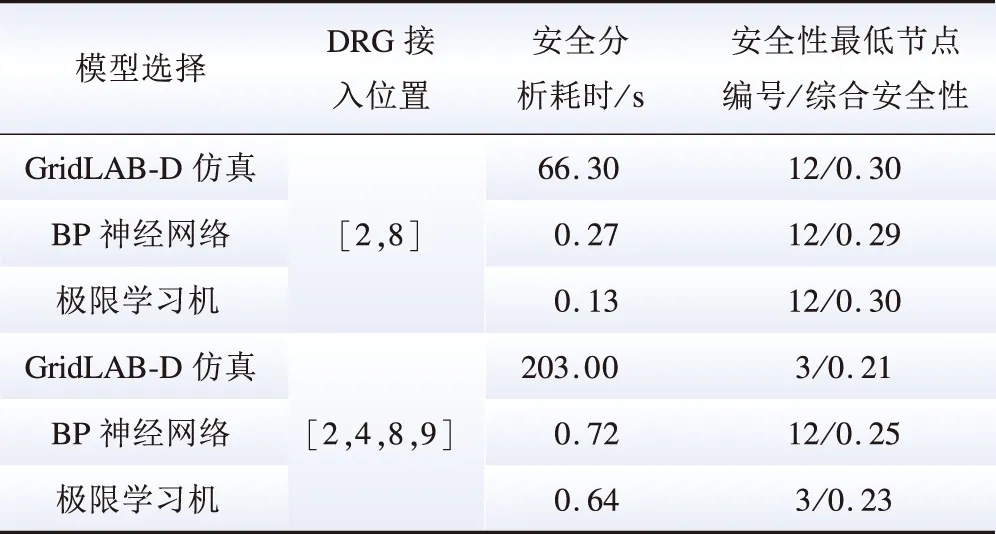
表3 不同规模DRG分析结果比较Table 3 Comparison of analysis results with different amount of DRG

上述结果表明本文ELM模型相比于BP神经网络的安全分析能够适应更大的场景变化及负荷波动。表3同时显示，接入位置也会影响安全分析结果，安全分析应随着有源配电网DRG渗透率的增加更新，用于指导新增DRG的安装位置。

3.1.4 训练集大小对不同模型的计算结果影响分析

在有源配电网中，馈线终端单元(feeder terminal unit，FTU)负责实时采集配电网运行信息并上传到控制中心[33]，受到采集步长等因素的限制，采集潮流数据时间成本较高。以15 min采集步长为例，采集4 000条三相潮流数据样本大约需1 000 h，而采集50条数据样本仅需约12 h。随着DRG渗透率不断提升，有源配电网络的拓扑结构变化的频度提高很多的情况下[23]，需要模型能够迅速地完成更新。

本节对本文ELM模型在不同规模的训练集下的效果进行评估。首先选取4 000条三相潮流计算数据集作为标准训练集；之后从中随机选取50条作为小规模训练数据集，代表不同时间尺度内采集到的数据集，分别对BP神经网络及极限学习机模型采用上述2个数据集进行训练，比较上述2种模型在测试集上的计算结果。其中，BP神经网络随迭代次数的变化如图4所示。

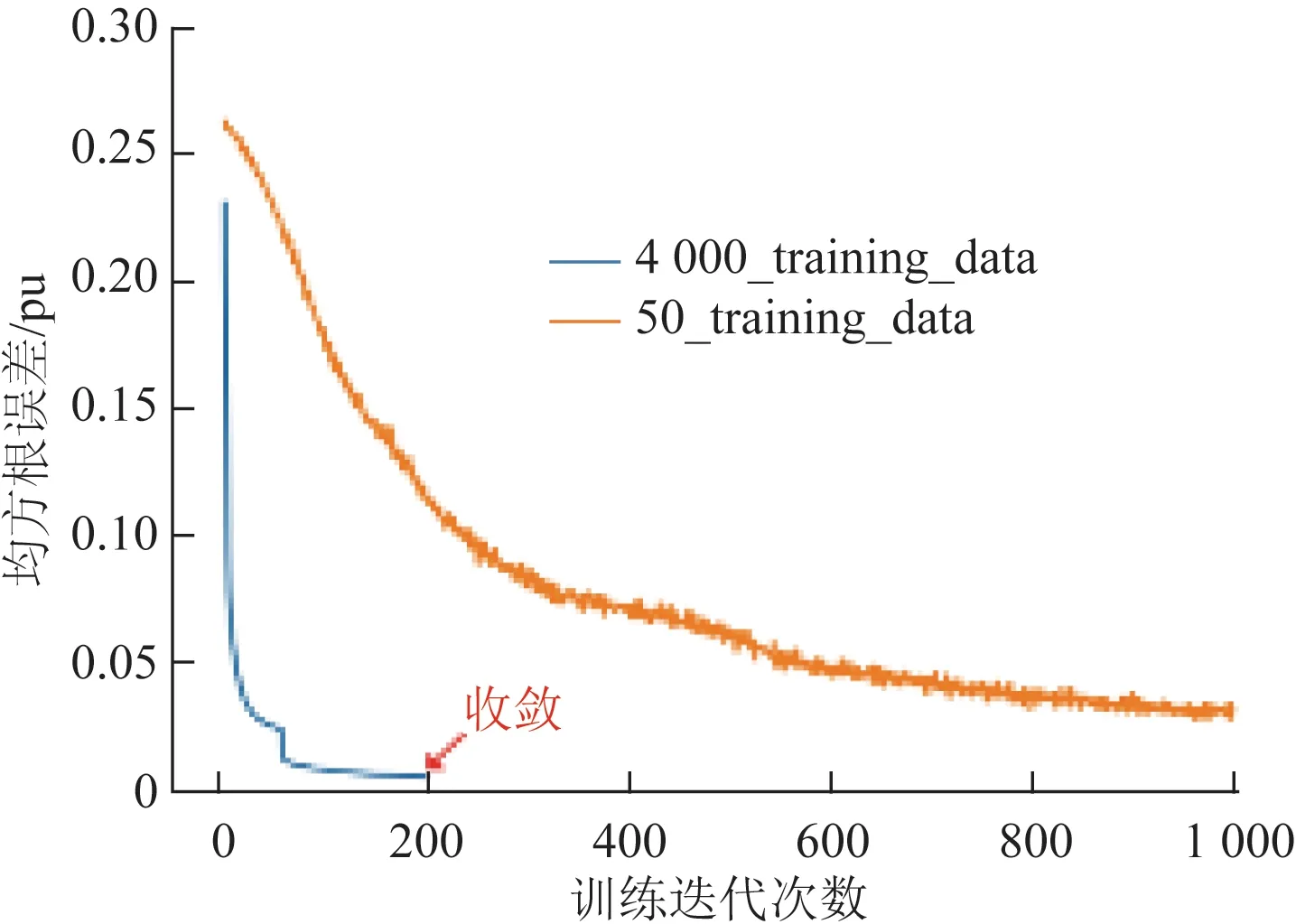
图4 Cost随迭代次数变化情况Fig.4 Cost changing in training process

图4表明，在缺少训练数据的情况下，BP神经网络模型的准确性出现了较为明显的波动，为了补偿训练数据过少带来的影响，反复利用同一组训练数据进行更多次数的迭代也容易导致过拟合的出现，测试集上均方根误差的扩大也说明了这一结果。而极限学习机模型在不同的训练集下表现出来的拟合效果没有明显差异，不同训练集下的不同模型性能比较如表4所示。

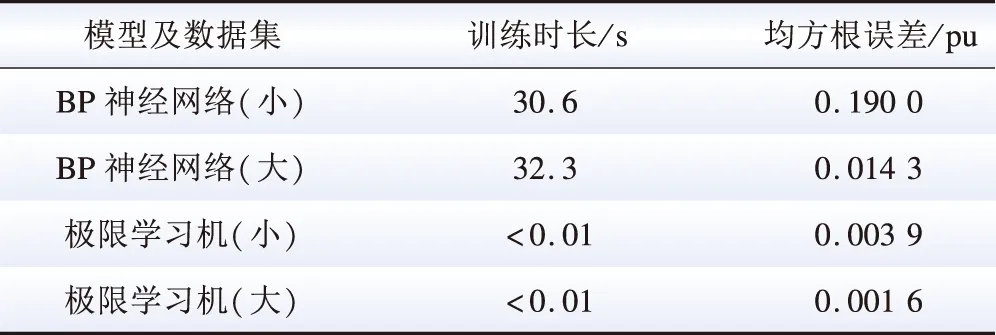
表4 不同规模数据集下的模型性能对比Table 4 Comparison of models under different training data

3.1.5 测试集范围对不同模型的计算结果影响分析

由于负荷及新能源的不确定性，配电网运行实际数据可能超出训练集数据范围，对本文提出采用ELM的方法与传统BP神经网络方法在不同数据范围测试集上的最大误差进行比较，结果如图5所示。

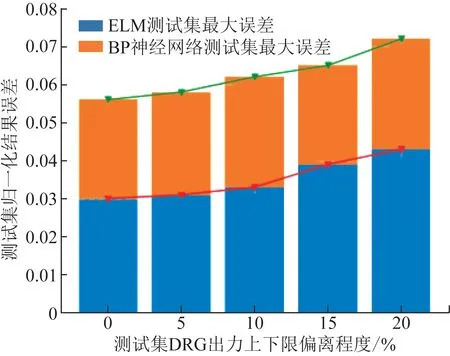
图5 测试集范围对误差的影响Fig.5 Effects of test set scope on error

图5中横坐标测试集边界范围表示测试集DRG出力的上下限波动范围。图5显示，当测试集DRG波动范围处在20%以内时，本文提出的运用ELM进行潮流计算的方法要优于采用传统的BP神经网络，最大误差约为4%。ELM模型明显具有更优的性能。

3.2 有源配电网节点安全分析

目前，电网波动的主要原因之一是DRG电源的单相接入，因此算例中仅考虑单相接入的情况。根据前文的分析结果，本文中极限学习机模型隐层单元个数最终选取为100个，输入数据为网络所有节点的三相负荷，输出数据为所有节点的三相电压。

根据图2所示的流程，对IEEE 13节点网络进行安全分析耗时0.13 s，可实现秒级安全分析。各个节点的得分如表5所示，分析过程中各节点的电压幅值、三相不平衡度如图6、7所示。

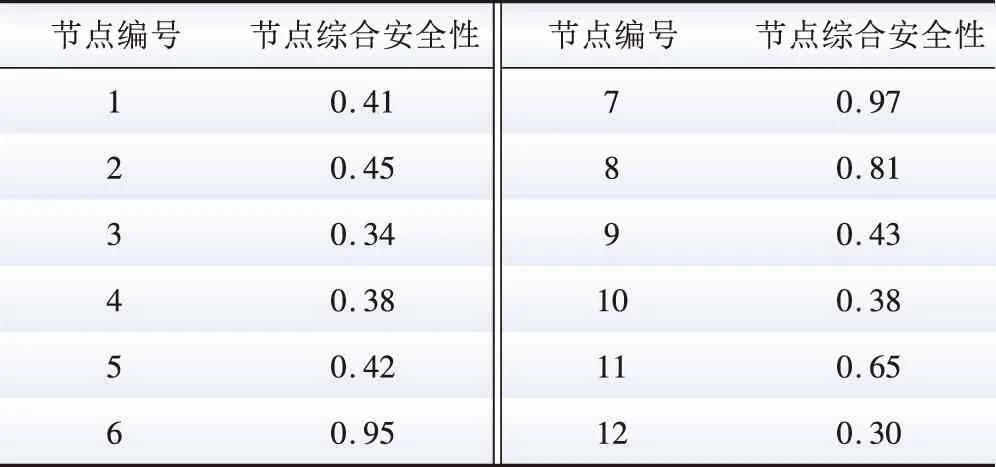
表5 各节点综合安全性计算结果Table 5 Calculation result of composite safety for each node

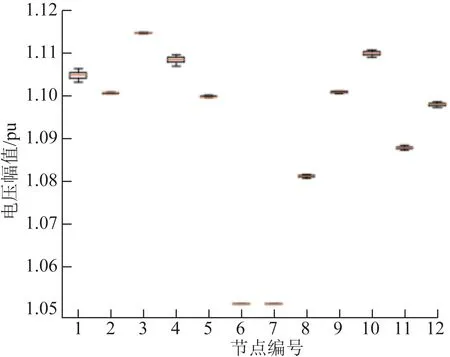
图6 各节点电压幅值分布Fig.6 Voltage distribution at different nodes during analysis

从图6和图7中可以看出，节点3的电压越限程度最高，以标幺值统计达到1.115 pu，高于1.10 pu的安全水平。节点12的电压越限情况则接近1.10 pu，处在越限边缘。但节点12的三相不平衡现象严重，达到了0.33，远高于其余节点0.15以下的水平，导致表5中节点12的综合安全性最低，该节点容易因新能源波动产生安全问题，配电网运营商需要在日常运营和技改项目设置中进行格外关注，例如通过拓扑调压缓解DRG带来的冲击[23]。节点7的综合安全性最高，在新能源波动情况下，风险场景出现较少，风险节点12在不同场景下电压如图8所示，横轴表示对应电压水平在场景统计中的出现次数。

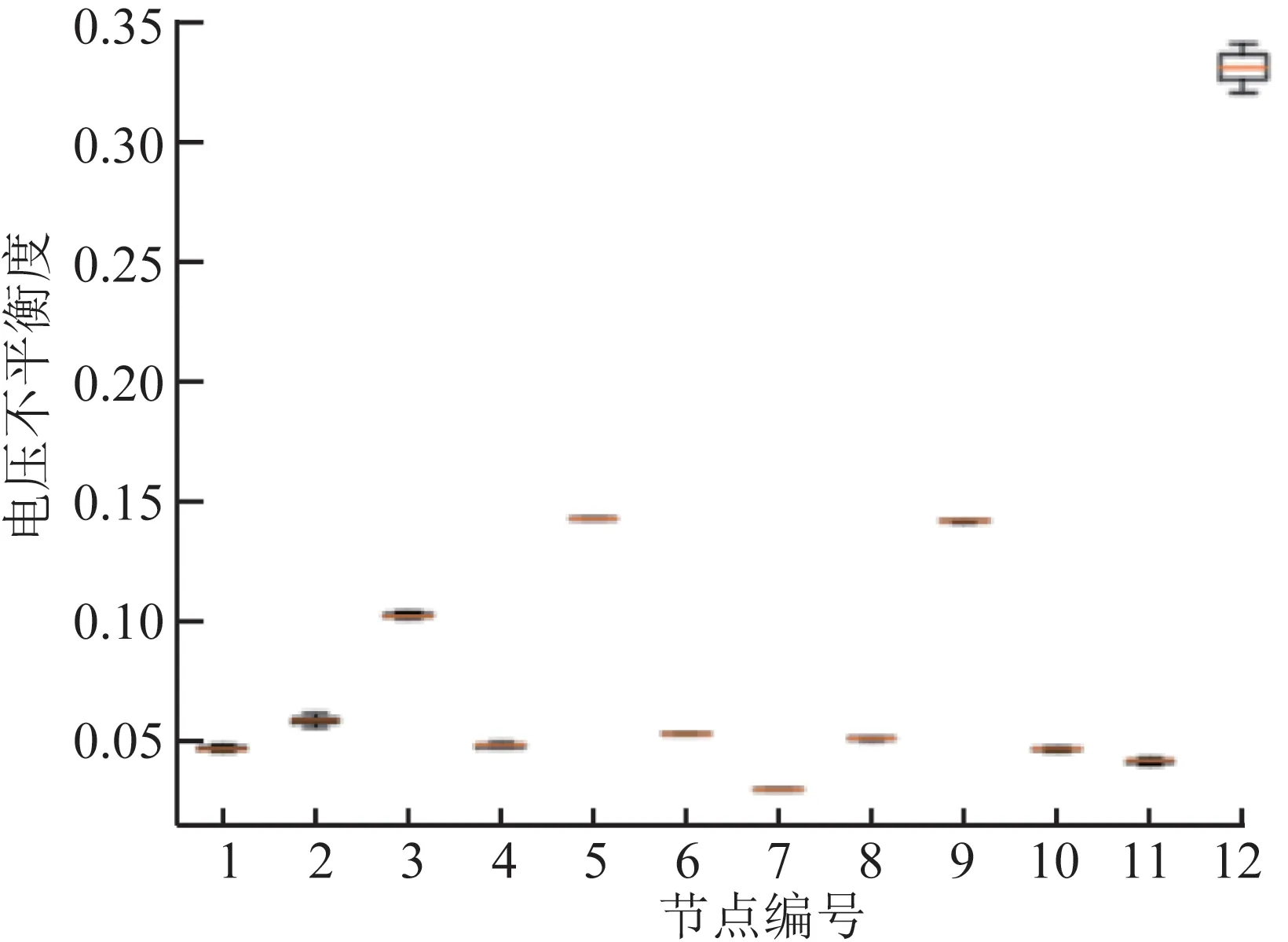
图7 各节点电压不平衡度分布Fig.7 Distribution of voltage imbalance at different nodes

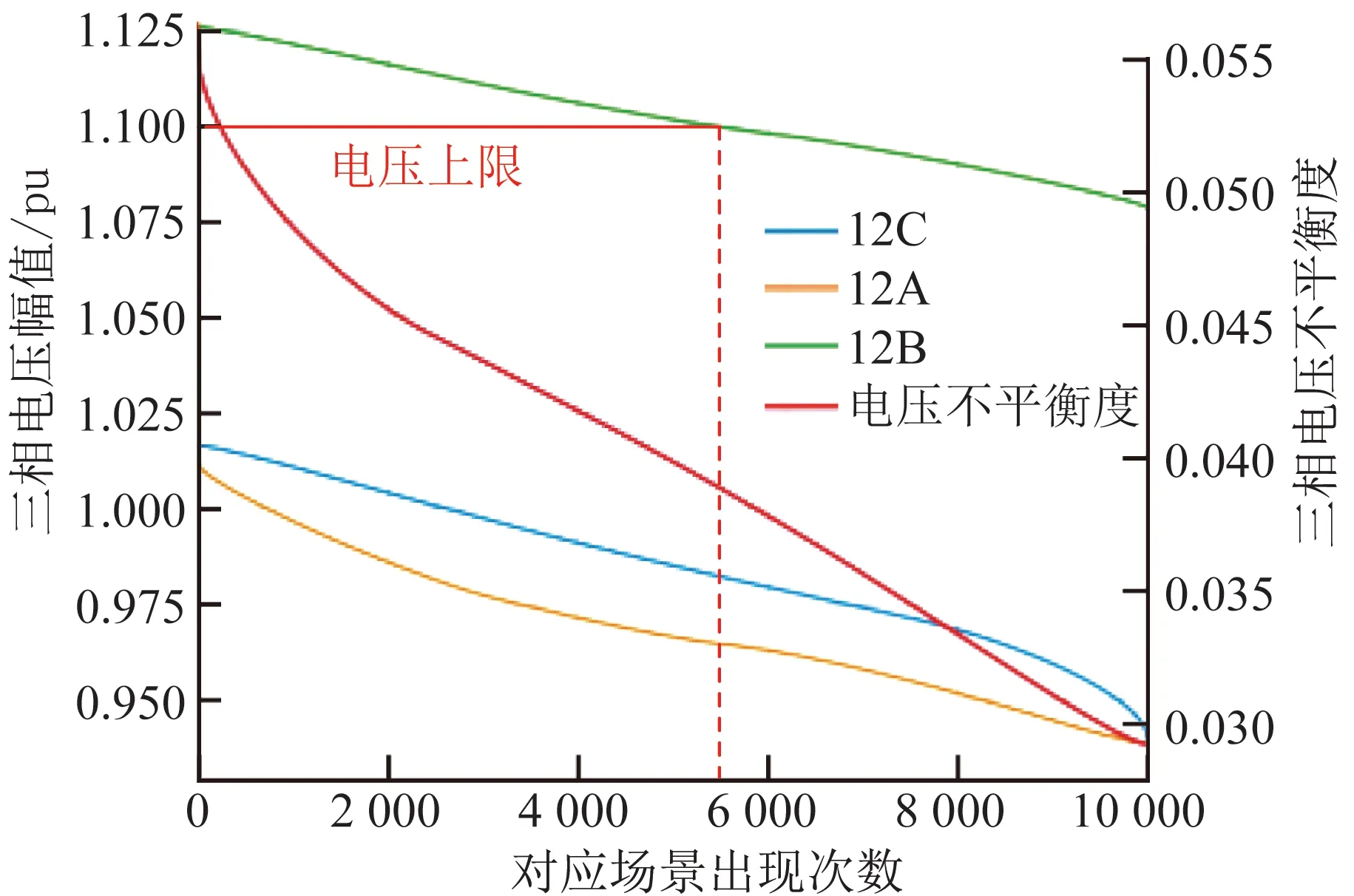
图8 不同网络负荷下节点12三相电压幅值及不平衡度变化Fig.8 Voltage and imbalance variation at node 12 with different net loads

在更大规模的配电网络中，本文提出的电压静态电压安全分析方法仍然适用。在图9所示的IEEE 33节点配电网中，分布式光伏安装在2、4、14、28这4个节点，安全分析模型的时间效率及结果如表6所示。在IEEE 118节点配电网中，安全分析结果如表7所示。

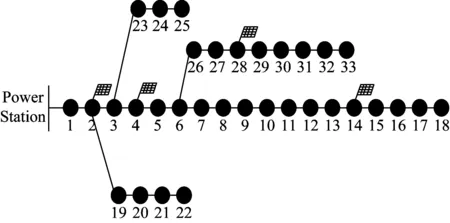
图9 IEEE 33节点网络示意图Fig.9 IEEE 33-node system

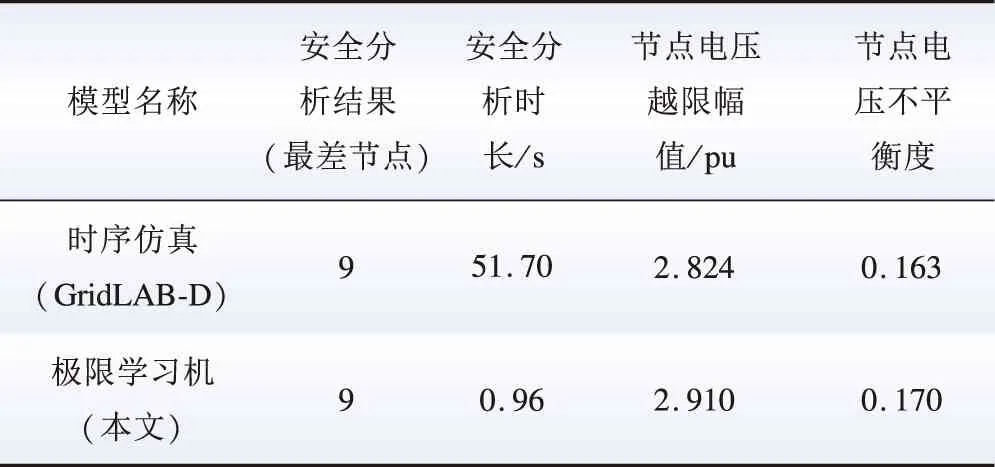
表6 IEEE 33节点配电网下的电压安全分析结果Table 6 Analysis of voltage safety in 33-node distribution network

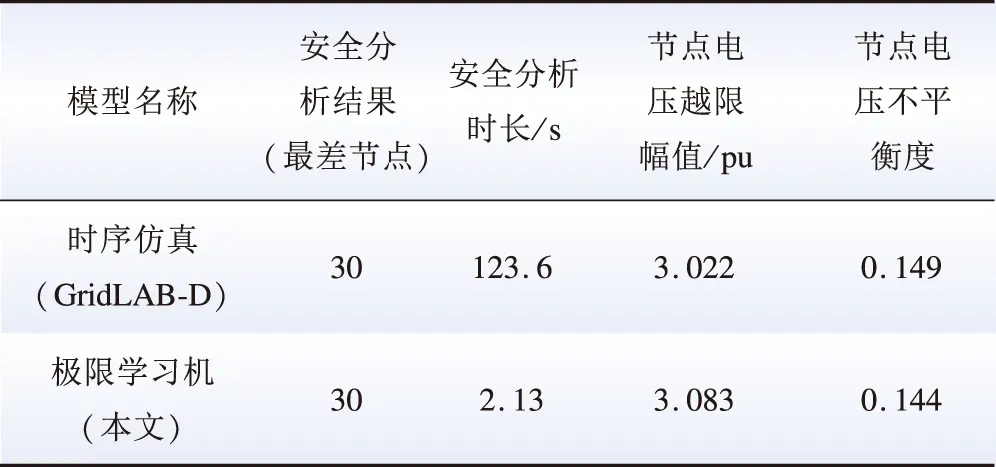
表7 IEEE 118节点配电网下的电压安全分析结果Table 7 Analysis of voltage safety in 118-node distribution network

表6与表7显示，本文所提出的基于极限学习机的安全分析方法，在更大规模的配电网中依然适用。其中，118节点配电网络的参数由附录A给出。实验结果显示，本文所提出的方法一方面在时间效率上比传统的时序仿真方法具有较大提升；另一方面，在准确性上，本文所提出的方法要优于BP神经网络的安全分析方法，在实际的工程应用中具有更高的实用性。

4 结 语

针对分布式发电迅速发展，新能源波动及其不平衡并网对配电网安全带来的冲击，本文提出了基于ELM算法的三相潮流计算，并进行配电网静态电压安全分析。相对于传统的三相潮流计算，该方法计算潮流的效率更高，减少了运算时间，克服了传统算法中的收敛性能问题，将安全分析问题拓展到三相也使得结果具有更高的可信度。并且相比于传统BP神经网络节约了大量的训练时间成本，在网络拓扑结构发生变化时也能短时间内给出分析结果，具有一定的工程意义。对于指导分布式风光发电安装、引导运营及技改层面的改造工作、保障配电网安全运行、辅助智能配电网安装灵活性调节装置、进行需求侧管理，从而应对DRG深度接入对配电网带来的冲击具有重要现实意义。