基于加权平均插值和容积卡尔曼滤波的配电网预测辅助状态估计

2021-08-11柴林杰蔡亦浓高铭郝运陈继开李江

电力建设 2021年8期

柴林杰,蔡亦浓，高铭，郝运，陈继开,李江

(1.国网河北省电力有限公司经济技术研究院，石家庄市 050021；2.东北电力大学电气工程学院, 吉林省吉林市 132012)

0 引言

配电网状态估计是通过冗余量测信息实现状态的预测和估计，是配电网分析和其他高级应用的基础[1]。远程终端(remote terminal unit, RTU)设备作为配电监控与数据采集系统的核心设备，采集数据主要包括电流有效值、有功功率、无功功率、功率因数等稳态参数，已广泛应用于调度自动化系统[2]。近年来，微型同步相量测量单元(micro synchronous phasor measurement unit，μPMU)已被开发出来，能够实时采集电压和电流相量，可实现广域保护，未来有望在配电网中大规模配置[3]。μPMU与RTU采集的数据虽然应用场景不同，应用系统相互独立，各有优点，但也存在联系。将μPMU与RTU数据深度融合，可显著增加配电网观测性，可为开发配电网高级应用软件提供支撑。与输电网不同，配电网的状态更加复杂多变，具有支路多、线路短、电压波动小等特点[4-5]，其状态也更多依赖电流的量测信息[6]。

预测辅助状态估计(forecasting aided state estimation，FASE)，是在准稳态工作条件时，反映发电机和其他控制器缓慢变化的状态估计[7]。FASE具有状态估计和预测功能，具有更强的数值稳定性[8]。为了解决配电网节点多、维数高的问题[9],文献[10]应用解耦技术将功率型量测数据转化为电流相量进行状态估计。由于功率型量测构成非线性量测方程，具有迭代过程复杂、误差大等问题。文献[11]将支路电流的幅值和相角作为变量进行状态估计。文献[12]提出了一种快速解耦的配电网电流估计方法，该方法可减小雅可比矩阵计算次数，减小计算量，但误差仍然较大。

当μPMU和RTU同时存在时，状态估计的数据来源更加多元，系统可观性大幅提高，但也存在数据不同步的问题，需要解决混合数据融合问题。为解决该问题，文献[13]提出一种基于非线性估计模型，对混合数据进行非线性迭代计算和坏数据预处理。然而，μPMU量测计算权值的确定和相角参考点的选取问题很难解决。文献[14]提出了一种基于混合量测估计方法，在非线性状态估计的基础上进行二次线性状态估计，未对不同周期数据进行深度融合。

本文针对μPMU和RTU混合数据进行深度融合，提出配电网预测辅助状态估计新方法。首先，采用数据填补技术解决混合数据更新周期差异问题；然后，采用容积卡尔曼滤波，提出混合数据估计和预测的FASE算法；最后，仿真验证所提算法的有效性。

1 RTU量测的数据填补

在工频50 Hz电网中，RTU数据的更新周期一般为1 s，而μPMU测量数据的更新周期为20～200 ms[15]。图1为不同更新周期下的μPMU和RTU数据。

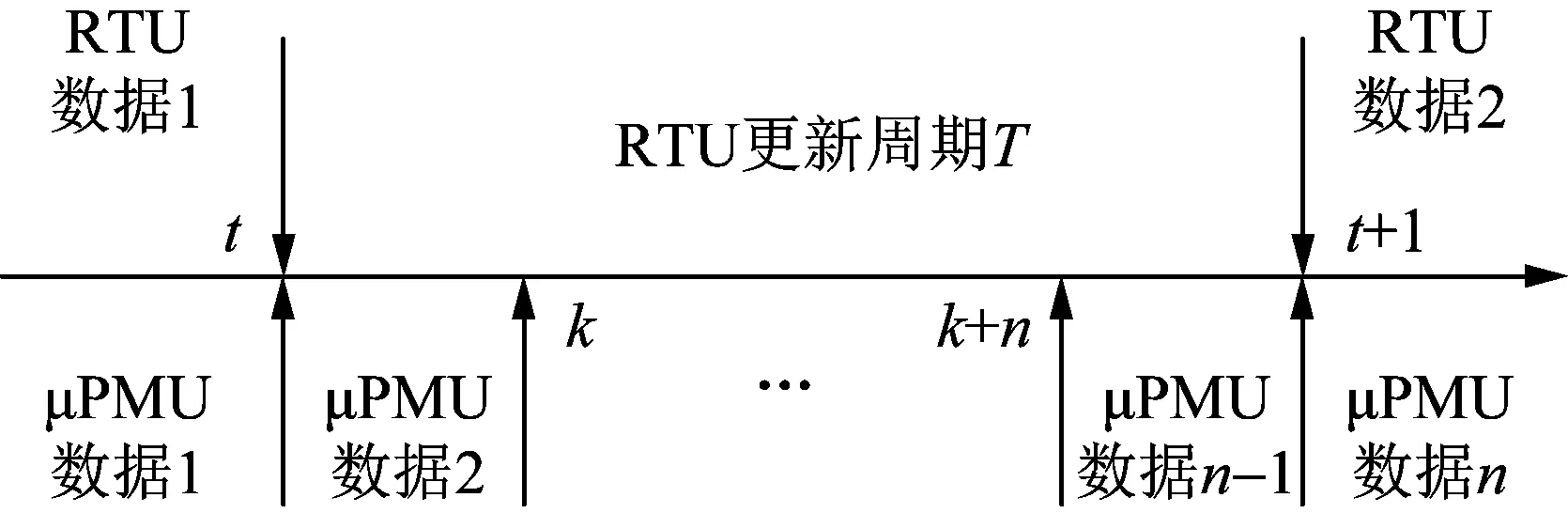
图1 RTU和μPMU数据的更新周期关系Fig.1 Update cycle relationship of the data from RTU and μPMU

图1中，μPMU相对于RTU具有更高的量测精度，更短的更新周期。针对混合数据，有必要对RTU进行数据填补，使得不同更新周期的数据保持同步。本文根据μPMU数据和RTU历史数据，实现RTU数据填补[16]。

1)线性插值。线性插值(linear interpolation，LI)是根据前一时刻值xRTUh和后一时刻值xRTUj估算出i时刻的空值xRTUi，即：

(1)

LI方法虽然简单，但当空数据增加时，精度会显著降低。

2)历史平均值插值。线性插值简单有效，但在前后数据间隔较长时插补效果不显著。历史平均值(historical average，HA)插补采用历史数据，可以确保插值的数值稳定性。基于附近其他量测设备的历史数据，根据基尔霍夫电压和电流定律，近似作为缺失时段xRTUi的历史数据，实现RTU数据的填补，公式如式(2)所示。

(2)

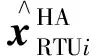
3)最优加权平均插值。最优加权平均(optimally weighted average，OWA)插补的优势在于对短周期和长周期都具有良好的精度[16]。两个样本点之间的数据可以通过OWA插补进行估算，RTU的LI插补值和HA插补值的加权，即：

(3)

2 混合量测数据的状态估计

当系统工作在准稳态时，发电机和其他控制器变化缓慢，其动态过程忽略不计[17]。这种情况下，状态转移可由平滑参数决定。因此，准稳态方程包含测量方程和状态转移方程，如式(4)所示。

(4)

式中：xt表示时间t的n维状态向量；zt+1代表时间t+1的m维测量向量；wt表示均值为0的高斯过程噪声；Qt是过程噪声误差协方差；εt+1是零均值的高斯测量噪声；Rt+1是测量噪声；误差协方差f(·):Rn→Rn和h(·):Rm→Rn分别是n维状态空间中的状态转移函数和m×n维测量空间的非线性函数。

2.1 μPMU量测方程

对于μPMU量测节点，测量数据以极坐标的形式呈现。根据极坐标电压电流相量U∠θ与I∠θ，转换成式(5)表示的直角坐标变量。

(5)

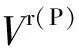
2.2 RTU量测方程

对于RTU量测的三相功率，有功功率P和无功功率Q可表示为：

P=VRTUIRTUcos(fRTU)

(6)

Q=VRTUIRTUsin(fRTU)

(7)

式中：VRTU和IRTU分别表示电压和注入电流有效值；cos(fRTU)是RTU功率因数。功率也可以用电压和电流的实部和虚部表示：

P=VRIR+VIII

(8)

Q=-VRII+VIIR

(9)

式中：VR、IR分别表示电压、电流实部；VI、II分别表示电压、电流虚部。

可将RTU测量转换为等效注入电流，等效电流测量转换成式(10)和式(11)。

(10)

(11)

式中：Ir(eq)、Ix(eq)分别代表等效注入电流的实部和虚部。

对于来自RTU的电流测量值，为了减少由于相角信息而导致的误差，将支路电流的平方用作等效支路电流测量，如式(12)所示。

Ieq=(IRTU)2

(12)

式中：Ieq表示等效变换后的支路电流测量值。

将RTU的三相节点电压量测值等效变换为:

(13)

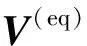
2.3 混合量测方程

电压和电流相量量测数据通过坐标转换，直角坐标系下的混合测量变量ZM为：

(14)

具体测量数据如式(15)所示：

(15)

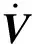
(16)

式中：上标r表示实部；上标x表示虚部；P表示μPMU量测；l表示支路号；i、j分别表示首末节点号；eq表示等效变换后的量测。

2.4 状态转移方程

定义状态变量为：

(17)

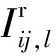
Holt’s双参数指数平滑法被用来近似代替状态转移方程式(4)。该方法使用2个平滑参数，即平滑原始序列的时间趋势α和趋势增长β。Holt’s双参数法，具有灵活性大、结构简单、整体效果好的优点[18]。Holt’s双参数法的状态转移方程如式(18)所示[19]。

(18)

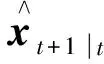
3 容积卡尔曼滤波

3.1 容积卡尔曼滤波基本原理

针对节点数量多、维数高的复杂网络，容积卡尔曼滤波(cubature Kalman filter,CKF)相较于卡尔曼滤波，具有更好的精度和稳定性。CKF的基本思想，是通过高斯加权积分的三阶球面径向容积定律，采用逼近积分项，实现不同方向上的概率性滤波[20]。球体的径向体积规则将为2n维状态变量产生4n个等权体积点，所有等权体积点以原点为中心均匀分布在球体上[21]。

非线性状态方程和高斯概率密度的乘积积分表达式如下：

(19)

式中：I2N(f)表示待求解的积分项；ξi是容积点；R2n为2n维积分域；wi=1/(4n)是相应容积点的权值，其中n为状态变量个数。容积点ξi的表达式为：

(20)

式中：[e]i表示容积点集中的第i个元素。本文的容积点集中的第i个元素为：

(21)

3.2 状态预测和修正

CKF的状态估计由状态预测、测量预测和滤波校正3个步骤组成[22]。

1)状态预测。

容积点是利用已知前一时刻状态变量估计结果和误差协方差矩阵计算所得，如式(22)所示。

(22)

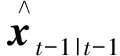
(23)

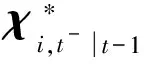
通过状态方程传播等权重的状态预测值容积点如式(24)所示。

(24)

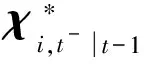
(25)

2)量测预测。

利用状态预测步中得到的状态预测值，计算等权测量预测的容积点，计算公式如下：

zi,t-| t-1=h(χi,t-| t-1),i=1,2,…，2n

(26)

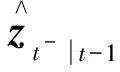
(27)

3)滤波修正。

根据状态预测和量测预测步的结果，预测协方差矩阵Pzz,t-| t-1和状态变量x与量测量z之间的交叉协方差矩阵Pxz,t-| t-1，计算公式如下：

(28)

(29)

式中：Pzz,t-| t-1为量测预测的协方差矩阵；Pxz,t-| t-1为状态变量x与量测量z之间的交叉协方差矩阵。

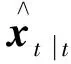
(30)

(31)

(32)

CKF的执行过程中不需要计算雅可比矩阵，而是利用容积点来近似后验概率分布。此外，CKF在计算过程中提出了球形对称分布的容积点，相关参数不会影响到容积点的权重。因此，CKF在数值稳定性和适应性方面具有很大优势。

为了提高CKF算法的适应性和鲁棒性，可采用文献[23]算法滤波。通过构造自适应因子在线修正协方差矩阵式(28)和式(29)。定义新息向量式(33)和新息向量矩阵式(34)，判断误差Δe和自协方差矩阵的迹大小。

(33)

(34)

根据判断结果构造自适应因子，在线校正自协方差矩阵和互协方差矩阵。表达式如下：

(35)

式中：tr(·)表示矩阵的迹。

采用式(35)，自协方差矩阵修正为：

(36)

同理，互协方差矩阵修正为：

(37)

4 混合测量数据下的FASE算法

4.1 混合数据的处理

基于RTU和μPMU异步混合量测，提出FASE算法。首先，对t和t+n时刻的RTU数据，使用式(3)的加权平均插值方法，实现RTU量测的插值，确保RTU量测值与μPMU同步。然后，建立混合量测的FASE数据模型(mixed-data FASE，M-FASE)，利用CKF进行状态预测与估计，执行预测及滤波修正步骤，确保数值的稳定性。混合数据预处理具体步骤如图2所示。

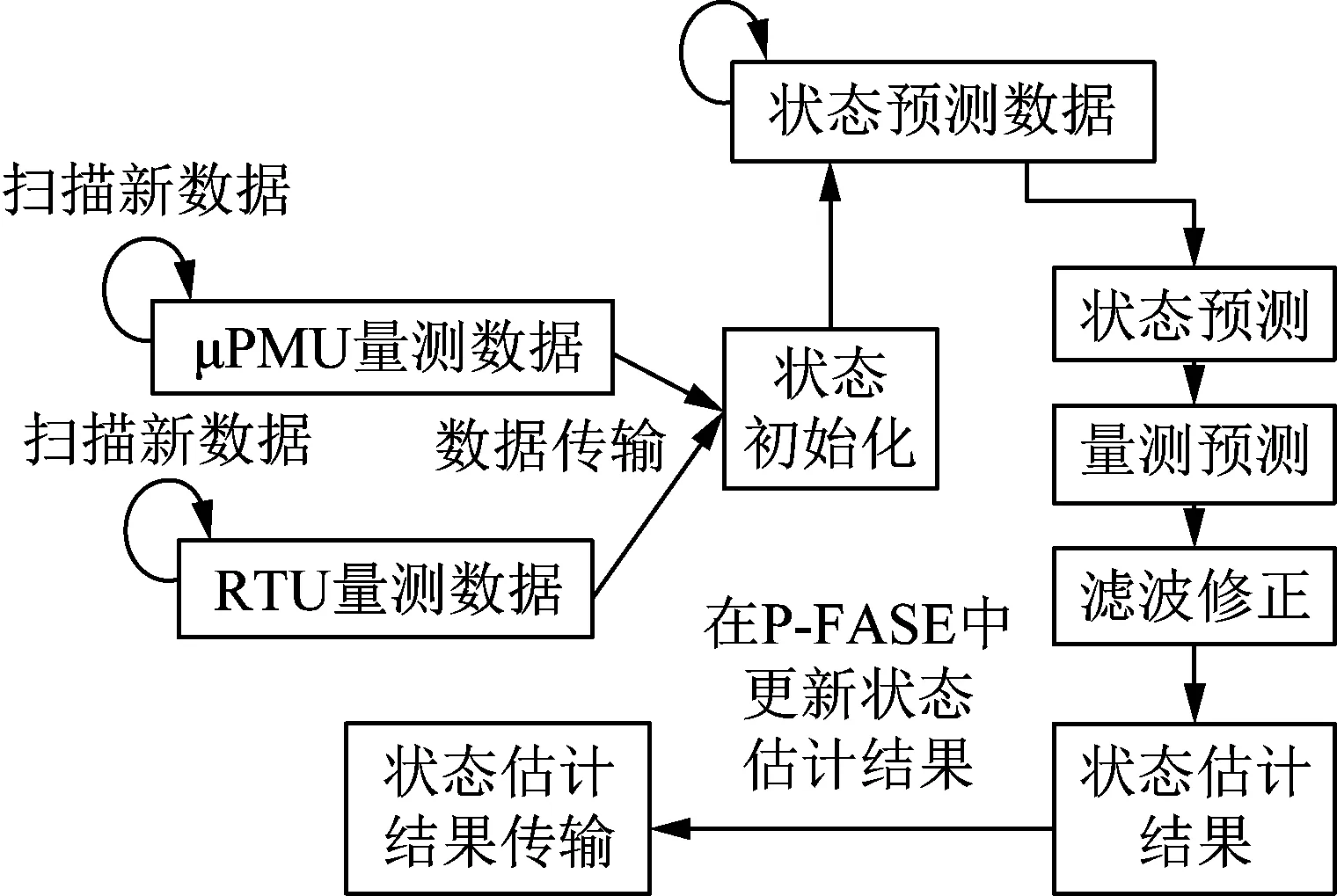
图2 混合数据预处理Fig.2 Diagram of mixed data pre-processing

4.2 FASE算法

结合4.1节μPMU和RTU混合数据的预处理，提出FASE算法如下，流程如图3所示。图3中，上标M表示混合量测的FASE变量。

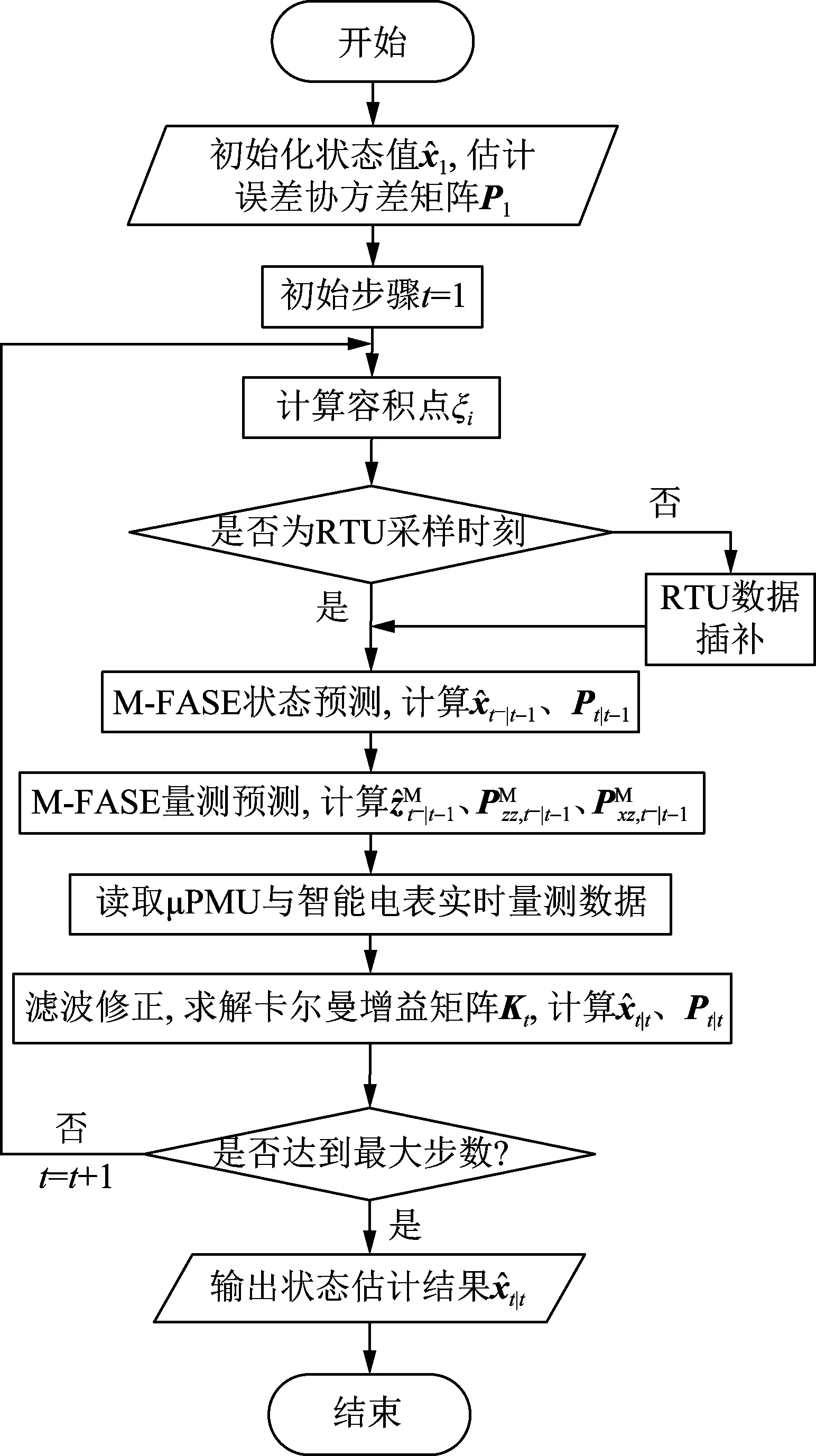
图3 预测辅助状态估计算法流程Fig.3 Flowchart of the proposed FASE

算法步骤如下：

2)通过等式(20)计算容积点ξi。

3)判断是否为RTU的采样时刻。如果是，则转到步骤4)；否则，执行RTU数据填补步骤。使用式(3)的OWA插补方法来填补空数据周期的RTU测量数据，确保RTU和μPMU的量测数据同步。

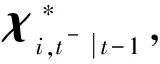
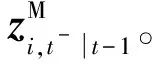
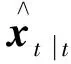
7)确定是否达到终止条件。若满足终止条件(设定接近于0的正数)或最大迭代次数(一般为10次)，则输出状态估计结果；否则，返回步骤2)。

4.3 评价指标

为量化所提算法的估计误差，在式(38)—(39)中定义了估计性能函数。

(38)

(39)

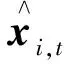
(40)

式中：ε是均方根误差；T是总采样次数。

5 算例分析

5.1 基本参数

采用图4所示的IEEE 37节点系统进行仿真分析。系统电压等级为4.8 kV，视在功率基准值为1 MV·A，光伏发电系统PV1和PV2额定容量为0.2 MW，分别连接在节点704和708。图4中，μPMU和RTU的量测节点分别用蓝色矩形和红色三角形标记。

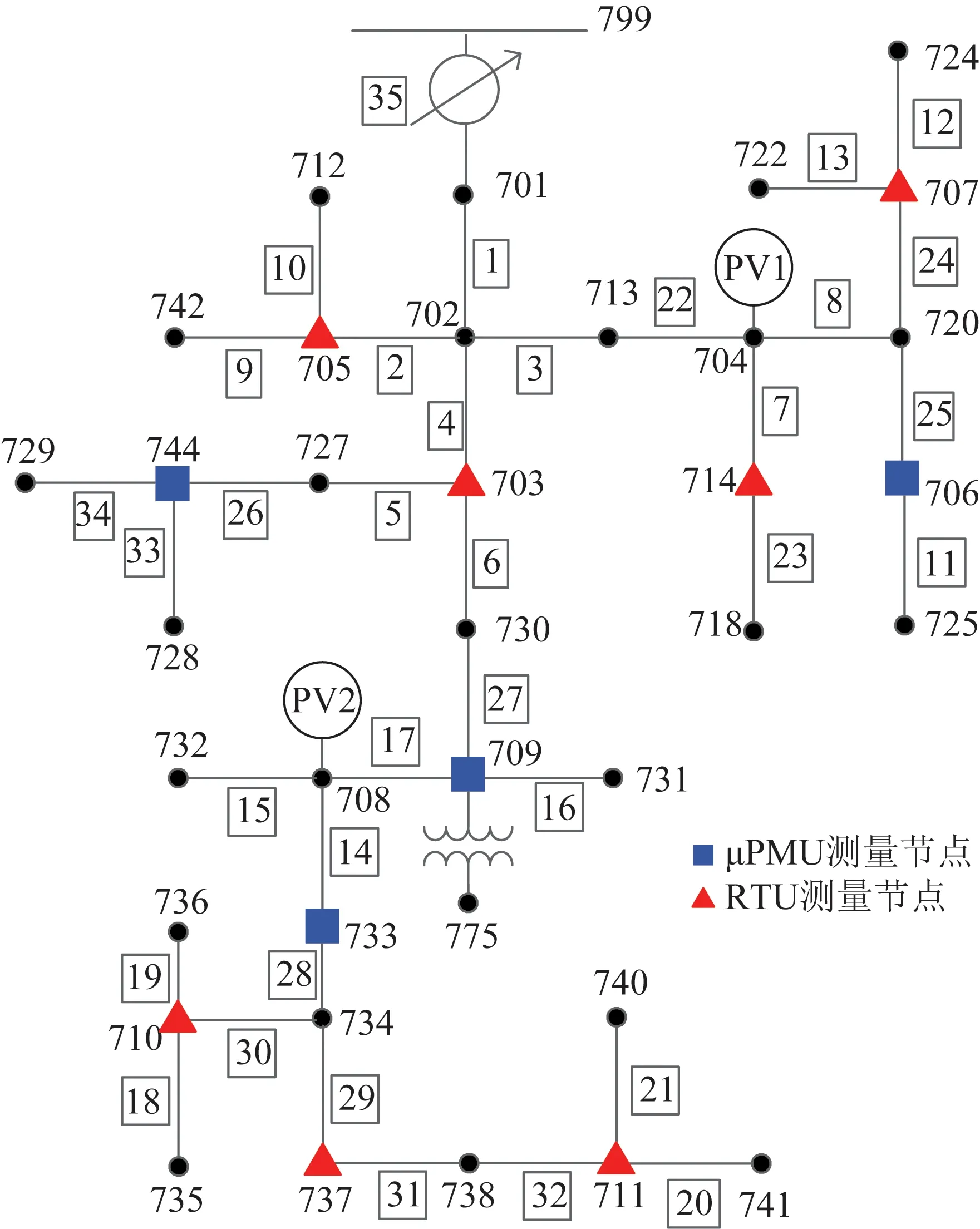
图4 IEEE 37节点系统Fig.4 IEEE 37-node system

μPMU和RTU的采样时间间隔分别设置为10 ms和1 s。在案例研究中，μPMU的相角偏差为0.002 rad，振幅偏差为0.005 pu，RTU测量的标准偏差为0.02 pu。双参数指数平滑法中平滑的参数如表1所示。

表1 三相平滑参数的取值Table 1 Three-phase smoothing parameter

5.2 综合误差分析

在算例系统中，比较CKF、无迹卡尔曼滤波(unscented Kalman filter，UKF)和扩展卡尔曼滤波(extended Kalman filter，EKF)下FASE的综合误差。经过CKF滤波、UKF滤波和EKF滤波算法后节点27的a相电流的实部和虚部如图5(a)和(b)所示。图5 (c)和(d)是每个采样时间a相均方根误差。

在图5中，使用CKF滤波的均方根电流误差为0.23%，而使用UKF滤波和EKF滤波的均方根电流误差分别为0.44%和0.79%，这表明CKF的应用效果优于UKF和CKF。在第30次采样后，EKF算法比其他2种方法产生较大的截断误差，EKF的滤波效果明显减弱。

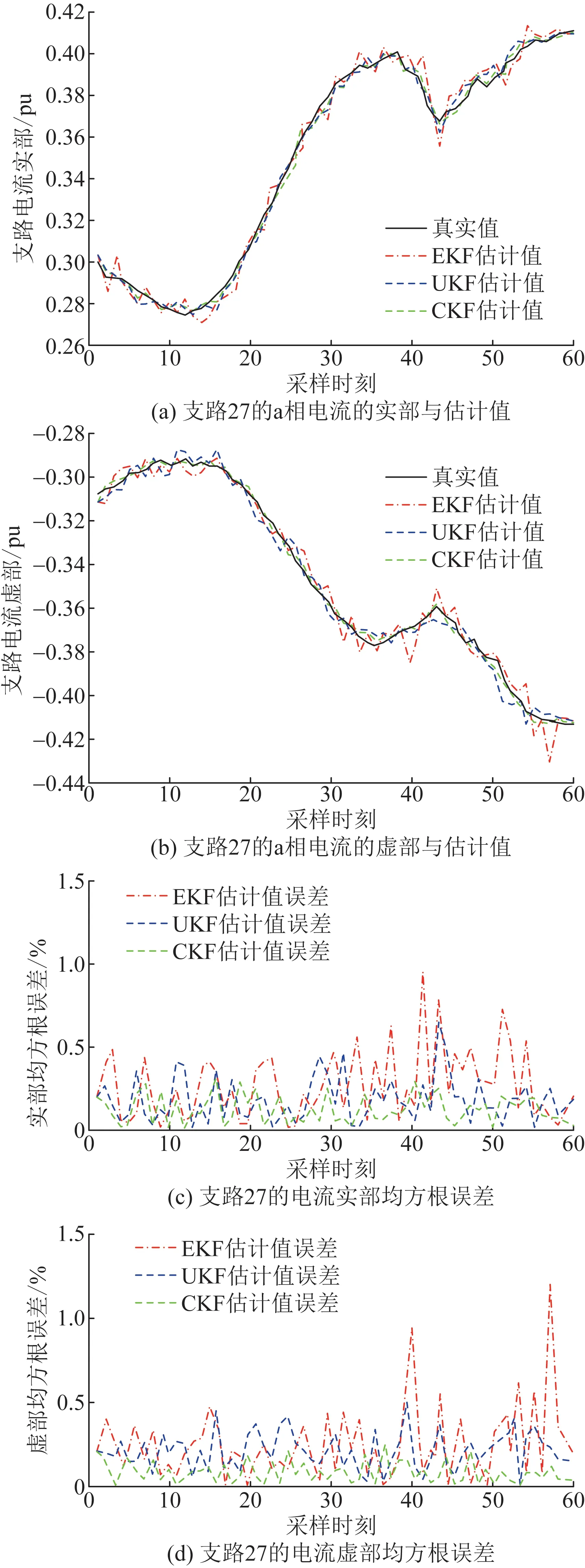
图5 支路电流的状态估计Fig.5 State estimation of branch current

在极坐标下采用不同滤波方法，a、b、c相电流幅值和相角的均方根误差对比如图6所示。在图6中，CKF下振幅的均方根误差平均值为0.18%，而UKF和EKF下的均方根误差分别为0.51%和0.82%。同样，CKF下相角均方根误差平均值为0.34%，而UKF和EKF下的均方根误差分别为0.61%和1.52%。结果表明，CKF法的精度高于其他2种方法，算法有更好的数值稳定性。

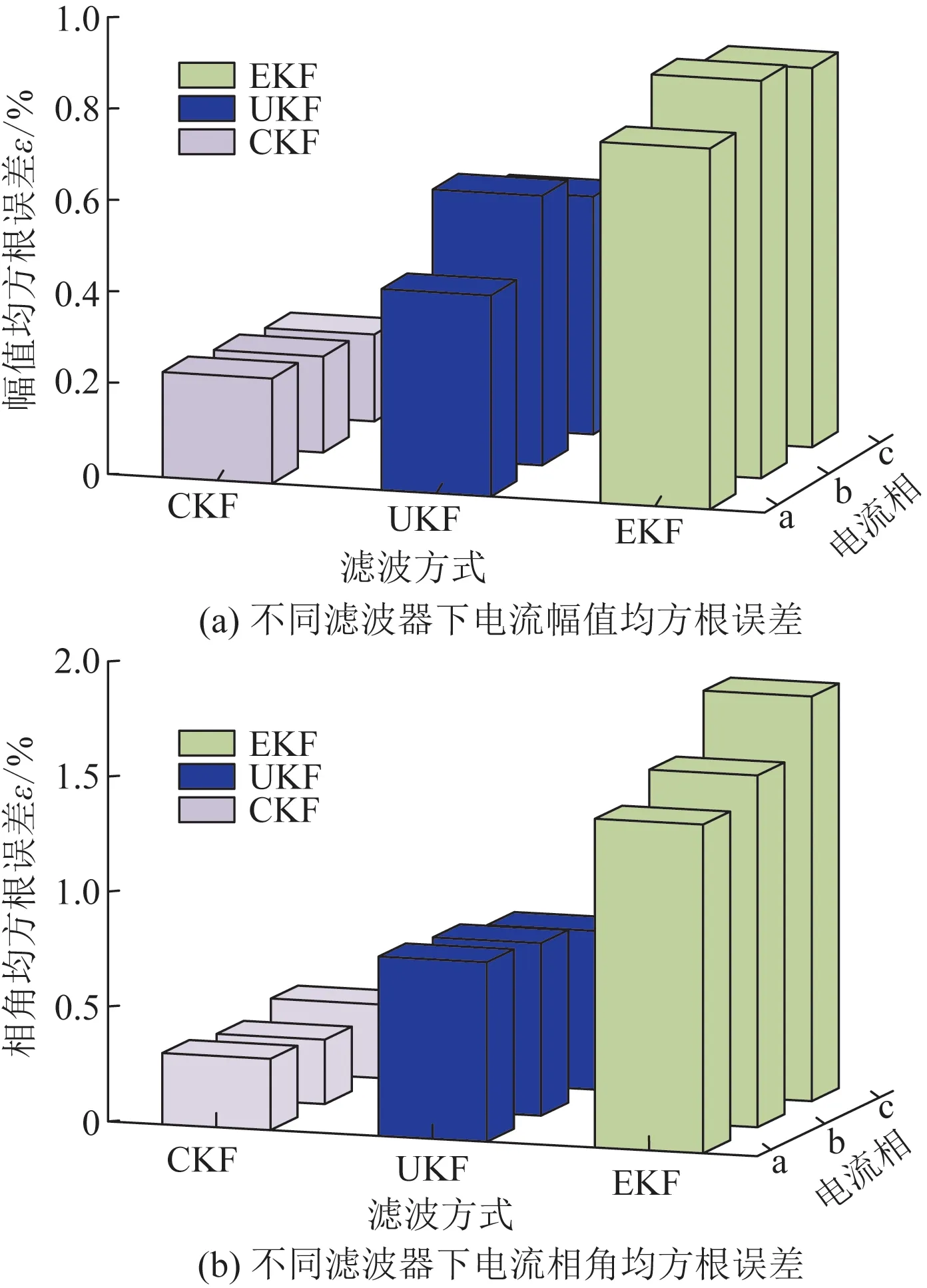
图6 三种滤波方法均方根误差对比Fig.6 Phasor estimation errors under different filters

5.3 计算时间

表2列出了使用CKF、UKF和EKF处理M-FASE循环周期内程序的执行时间。

表2 EKF、UKF和CKF的计算时间Table 2 Calculation time using EKF, UKF and CKF

由表2可知，使用3个滤波器的FASE执行时间小于1 s，这满足实时计算要求。使用EKF的计算时间是54.3 ms，计算时间最长，这是由于在卡尔曼滤波过程中，EKF需要额外的步骤来计算量测函数的导数，这增加了计算时间。CKF算法计算时间最快[24-25]，这是因为CKF算法的容积点和权重与非线性测量函数无关，并不需要UKF那样预先设置参数。因此，基于CKF的FASE的计算效率更高，满足实际要求。