基于蛇模型的管路三维重建方法

刘少丽，张文雄，吴天一，刘检华，王桢杰，胡佳

(北京理工大学 机械与车辆学院,数字化制造研究所，北京 100081)

提 要： 针对航空航天中大量应用的管路高精度快速测量难题，提出了基于蛇模型的管路三维重建方法.该方法充分利用管路灰度图像边缘特征，借助阈值分割和高斯滤波消除图像噪声，先结合蛇模型获取精准的管路图像边缘，贪心算法进行迭代以保证收敛效率，利用极线约束原理得到二维管路中心线点云，然后根据视觉投影原理，重建管路三维模型，最后使用多目视觉系统拍摄的照片进行结果优化以保证重建精度.结果表明：该方法对管路的测量精度为±0.15 mm，简便高效，无需过多的人工操作.同时，实现了管路圆弧段弯曲半径的测量，满足工业应用需求.

管路是航天器推进系统，热控系统，环控生保系统的重要组成部分，各系统的贮箱、阀门、推力器等零部件主要由管路连接而成[1].为保证管路的加工精度，在安装前需对管路进行快速精确测量.在管路测量过程中，需要精准、快速地获取管路直线段和圆弧段两部分信息.

传统的管路测量方法如靠模法和三坐标测量仪法有较大局限性.靠模法需要生产与管路相对应的模具，该方法无法测量形貌复杂的管路，也无法给出具体的测量结果，只能判断管路是否合格.三坐标测量仪法测量结果较为精确，但需要在管路表面获取大量点云信息，耗时较高，操作不便.

基于机器视觉的管路测量方法，为实现管路的快速准确测量提供了新途径.机器视觉进行管路测量的概念由Bosemann等[2-3]在1990年提出，基于CCD相机和AICON3D系统他们提出一种光学管路测量系统.该方法通过背光光源提高管路和背景之间对比度，并借助多目视觉拍摄重建进行测量.它能快速精准地检测不同种类和形状的管路，检测时间低于一分钟，精度高于0.5 mm.Wade等[4]提出一种用于加工过程控制和逆向工程的立体视觉测量方法，但测量精度和重复性值都低于0.1 mm.金鹏等[5]提出一种基于多目立体视觉进行复杂管路自动重构的方法，利用小圆柱体代替点云进行重建.Lee等[6]通过X射线图像重建3D管路模型.该方法通过波传播提取二维曲线并进行细化和平滑，利用极线匹配获取三维骨架.赵玉芹[7]提出一种在管路上贴标记点的方法辅助重建.然而该方法只能重建直线管路，同时贴标记点势必引入其他随机误差，降低测量精度.此外，Huang等[8]对管路测量也做出了较多工作.

现阶段机器视觉技术由于操作简便、重建速度快、精度高等特点广泛应用于管路测量领域，然而现有方法需要在测量前对管路进行预处理，如贴标记点或建立模型库.此外，现有方法主要对管路直线段进行重建，圆弧段则根据设计模型或用户输入弯曲半径等方法间接获取.本文提出了一种基于蛇模型的管路三维重建方法，借助多目视觉测量平台，实现了管路的全自动测量.尚未有文献在管路测量领域使用蛇模型进行管路的三维重建.该方法充分利用管路灰度图像边缘特征，借助阈值分割和高斯滤波消除噪声，结合蛇模型和极线约束原理获取二维管路中心线点云.根据视觉投影原理，重建管路三维模型，最后使用多目视觉系统提供的多角度拍摄图片进行结果优化.同时，测量结果包含全部的管路信息，弯曲部分由管路图像获取，而非设计模型信息等拟合生成.经实验验证，本文的测量结果误差在0.15 mm以内，测量时间在2 min以内，满足工业测量需求.

1 处理方法

本文提出的基于蛇模型的管路测量方法如图1所示，总体流程分为5步.

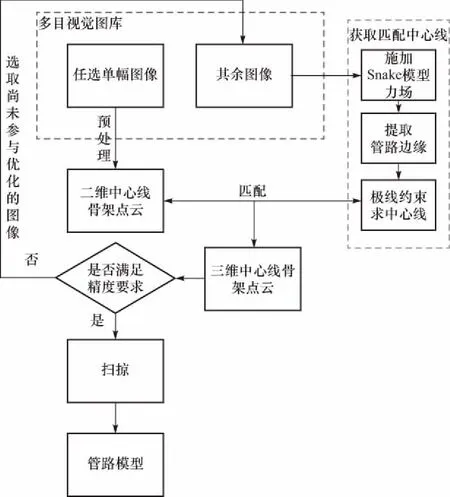
图1 测量流程图Fig.1 Measurement flow chart

① 从多目视觉测量仪器获取的管路图像中任选一张进行预处理，去除干扰并提取管路中心线点云.

② 引入第二幅图像，对图像进行预处理，并施加Snake模型力场，获取精准的管路边缘.

③ 选取第一幅图像中心线点云上任意一点，构建极线约束，并获取所选点在第二幅图像中的对应点.

④ 利用第一幅图像中心线点云的所有点及对应点构建空间点，获取管路的三维中心线点云.

⑤ 对优化结果进行判定，满足精度要求则输出三维中心线骨架点云，扫掠生成自由形状管路模型；若精度不够，选取其他图像重复步骤②～④，将获取的结果进行最小二乘拟合，继续判定是否满足精度要求.

1.1 二维中心线骨架提取

利用多目测量设备对目标管路进行多角度拍摄，任选多目图像中的一幅，如图2(a).由于拍摄环境问题，图像会存在很多额外的像素信息，例如设备边缘.同时，由污点、管路表面反光、表层破损等原因产生的图像噪声会对管路信息的提取造成干扰.故在提取骨架之前，需通过图像处理消除图片上的干扰.

图2 管路图像中心线骨架提取Fig.2 Extraction of centerline skeleton of pipeline image

背光光源使管路与背景区分度明显.利用此特征，通过灰度阈值分割单独提取出感兴趣区域.光源强度对管路提取有较大影响，光源太强导致管路表面反光，太弱则导致管路与背景对比度不足.针对本文测量实验平台，控制光源强度在合适范围内，管路灰度值区间为[80,100]，故管路区域分割以此为阈值.同时，为消除管路表面划痕和反光带来的噪声干扰，使用高斯滤波平滑管路表面，消去噪点，预处理结果如图2(b)所示.

由视觉测量投影关系知，管路在不同的投影图像中其中心线存在对应关系.但是，管路中心线投影在图像中没有显著的灰度特征，而边缘处的灰度变化明显，易于提取.故本文通过易提取的管路边缘，重建在各图像中有对应关系的管路中心线三维骨架点云.对预处理结果用Canny[9]算子提取图2(b)的管路边缘，并使用imerode功能[10]对边缘进行收缩和腐蚀，获取二维中心线骨架点云(如图2(c)所示)，用于模型构建和优化.

1.2 蛇模型提取亚像素精度边缘

蛇模型是图像领域内定义的一条参数化能量曲线，能在由曲线本身定义的内力和由图像定义的外力影响下移动.在内外力作用下，该曲线最终收敛至物体边界或物体目标特征，获取精准的物体边缘.相比于其他边缘提取方法，蛇模型有更好的鲁棒性，不受路面反光、划痕等情况影响. 1.1中图像预处理会丢失部分管路边缘信息，导致精度下降.利用蛇模型进行边缘提取，无需图像预处理，亦无需人工交互消除噪声影响，保证边缘提取精度.本文定义参数化能量曲线v(s)=[x(s),y(s)],s∈[0,1]为模型初始值.控制模型收敛的图像力为

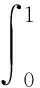
(1)

图像力E最低时模型收敛至最后结果.其中，受能量泛函形态控制的内力定义为

(2)

式中:v′(s)与v″(s)为参数化曲线v(s)关于s的一阶导数和二阶导数;α和β为控制一阶导数和二阶导数对收敛结果影响程度的权值,本文实验中，α=0.8，β=0.5.

不同于内力Eint，外力函数Eext受图像灰度特征和梯度特征影响，故Eext主要与图像中的目标物体参数(例如边缘)相关联.将灰度图像中像素点位置(x,y)与图像灰度的公式定义为I(x,y)，外力函数定义为

(3)

(4)

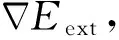
vt(s,t)=αv″(s,t)-βv‴(s,t)+V

(5)

用力场V(x,y)=[u(x,y),v(x,y)]作为矢量化的图片梯度.图片梯度将灰度特征通过力场形式表达出来，力场中所有的矢量均指向管路图像边缘.将外力力场施加至管路图像结果如图3所示.

图3 管路图像中的Snake模型力场Fig.3 Snake model force field in pipeline image

力场的最小化能量泛函可以表示为

(6)

(7)

(8)

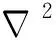
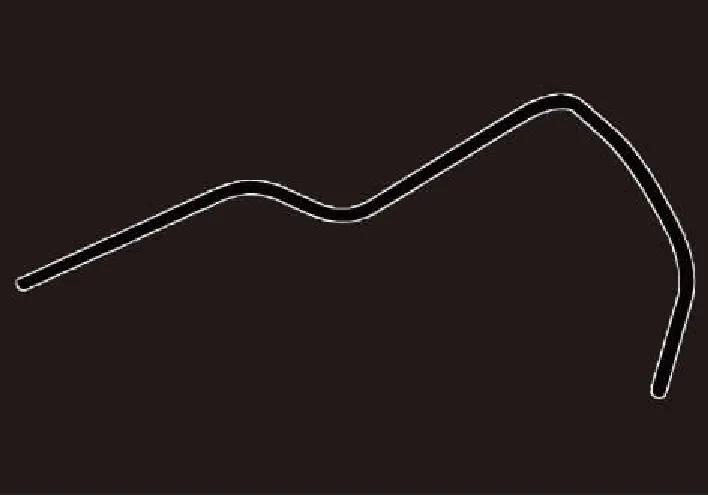
图4 Snake模型收敛结果Fig.4 Snake model convergence results

1.3 极线约束求取中心线点云

摄像机投影关系如图5所示，M为管路上一点.两幅图像分别由左右两摄像机拍摄，O和O′代表相机光心.任选图像1上一点m，直线Om必然与管路相交于该点真实空间点M.将直线Om投影到图像2，获得极线e′m′，极线与管路的交点必为M点在图像2中的投影m′.

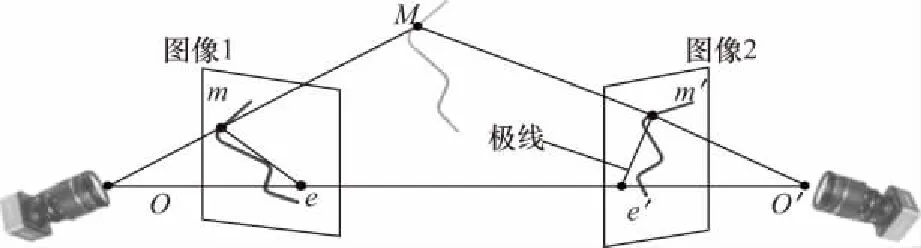
图5 极线约束原理Fig.5 Epipolar constraint principle

设点M的世界坐标为XM，在图像1和图像2中的像素坐标分别为u1和u2.设相机O投影矩阵为M11，相机O′的投影矩阵为M21，M点在相机坐标系下坐标为(Xc,Yc,Zc).根据摄像机投影原理得出以下转化关系

Zc1u1=M11XM

(9)

Zc2u2=M21XM

(10)

将M11分解为3×3矩阵M′11和3×1矩阵m1，M21同理.令XM=(XT,1)T并联立式(9)(10),消去矩阵X，得

(11)

定义m的反对称矩阵为[m]×，式(11)两边同乘[m]×.根据反对称矩阵性质[m]×m=0，化简为

(12)

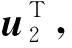
(13)

将一副图像中的点坐标代入式(13)，可以求取该点在另一幅图像中的对应极线.将2.1中点坐标代入式(13)，获取点在2.2中处理图像的对应极线.求取所有极线与图4交点的中点，可获取与图2(b)中点云相匹配且精度较高的管路中心线点云.

1.4 模型构建与优化

管路三维模型重建原理如图6所示.图像1为1.1中获取的二维中心线骨架点云.图像2为1.3中提取的基于蛇模型亚像素边缘的二维中心线骨架点云.

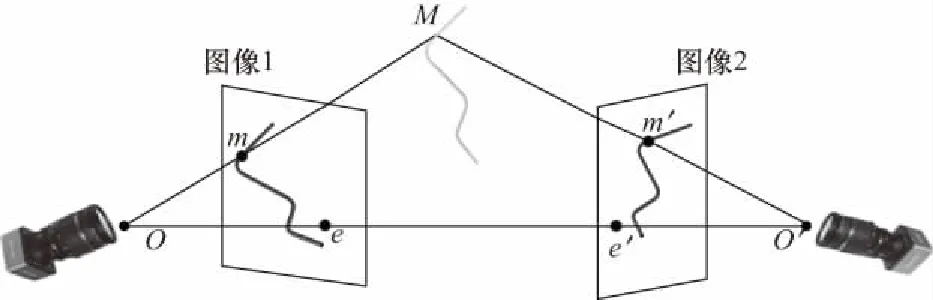
图6 三维模型重建原理Fig.6 Principle of 3D model reconstruction

根据视觉重建原理，通过点m和对应点m′，利用最小二乘法重建三维空间点M(X,Y,Z).重建式如下

(14)

将1.1中点云的所有点及1.3中所求的对应点代入式(14)，获取管路的三维中心线点云A.为进一步提高重建精度，需对该点云进行优化.在剩余图片中任选一幅图片，对其进行1.2、1.3的过程操作，并将结果带入式(14)获取三维中心线点云B.对点云A与B进行最小二乘拟合，获得点云C.同时，对点云C进行精度判定，若合格，则输出为最终结果；若不合格，则在剩余图片中任选一幅图片，继续迭代判定.

点云精度的判定标准为相机参与目数.通过实验验证，针对多数管路6目即能满足测量精度要求.本文实验中8个相机全部参与了三维重建，最终的重建结果如图7(a)所示.通过三维中心线骨架及管路截面半径，扫掠生成最后的重建模型，如图7(b)所示.

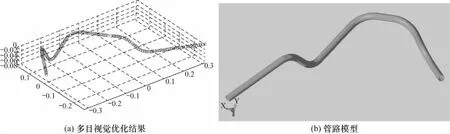
图7 重建结果Fig.7 Reconstruction result

2 实验验证

2.1 管路边缘提取实验

测量平台顶部分布8个相机，测量范围和相机高度如图8(a)所示.采用8个相机进行多角度拍摄能有效防止形状较复杂的管路出现自遮挡问题，确保管路图像信息完整性.相机为 Guppy F-146B型黑白工业摄像机，采用SONY逐行扫描CCD芯片，IEEE 1394数字视频信号接口，分辨率为1 388×1 038，靶面尺寸为6.4 mm×4.8 mm，像素数为1 392×1 040，像元尺寸为4.65 μm×4.65 μm.镜头选择Computar M0814-MP / M1214-MP，焦距为8 mm.

实际工程应用中，管路表面反光、划痕等情况会对管路边缘提取造成干扰.同时，相比于蛇模型，传统边缘提取算法更易受到干扰.蛇模型、Canny算子和Sobel算子提取管路边缘结果如图8(b)所示.

图8 管路边缘提取Fig.8 Pipeline edge extraction

根据实验结果，管路受光照影响时，蛇模型依然能提取目标边缘.而Canny算子和Sobel算子易受到干扰影响，提取多余的边缘，甚至提取错误边缘.故蛇模型有更好的稳定性，有效减少人工交互操作，提高测量效率.

2.2 管路测量实验

为验证本文提出方法的测量精度，将重建结果与三坐标测量仪测量结果进行比较.三坐标测量仪型号为HEXAGON-350AC，测量精度为1 μm，用于测量和拟合数据的操作系统为PC-DMIS.实验中管路为自由形状复杂管路，由多段直线与4个圆弧组成，如图9所示.通过本文算法求取被测管路的三维中心线点云，并将点云圆弧部分进行拟合，求取弯曲半径.利用三坐标测量仪在被测管路表面取点，拟合管路三维中心线点云，并进一步拟合4个圆弧半径作为标准值.同时，为验证本文方法的稳定性，改变被测管路位姿进行拍摄，共进行了25组测量.表1为实验测量结果，给出了其中5组测量结果、三坐标测量仪的测量结果以及本方法的精度和标准差.

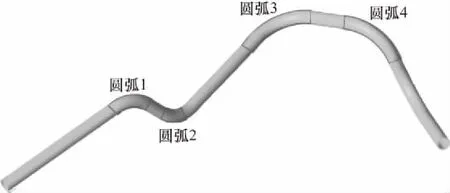
图9 待测管路Fig.9 Pipeline to be measured

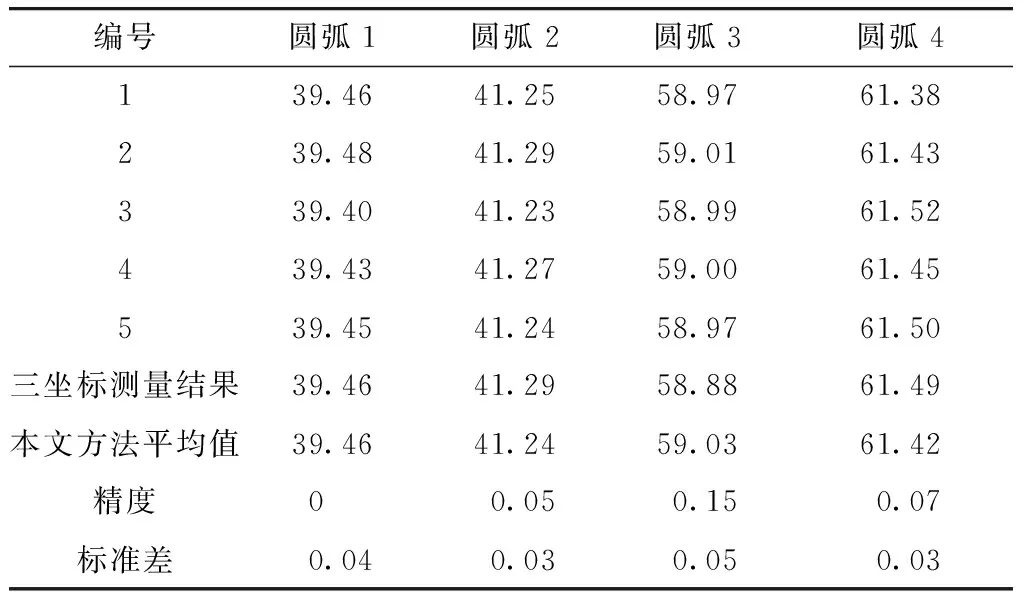
表1 测量结果对比

本文提出的测量方法重建过程均在2 min以内.测量结果表明，该方法的测量误差在0.15 mm以内，同时标准差在0.1以内，结果稳定.

3 结 论

本文充分利用管路图像边缘特征，借助蛇模型重建管路的三维模型.该方法解决了传统视觉测量需要提前输入管路模型信息、管路表面贴加标记点等预操作问题，提高了管路测量效率.为避免光照条件对边缘提取精度的干扰，本文使用蛇模型对管路图像进行处理.同时，该方法解决了管路圆弧段弯曲半径的视觉测量问题.为实现精确的模型测量，本文使用阈值分割和高斯滤波进行图像处理，消除了因拍摄背景和管路表面损伤带来的噪声干扰.借助多目测量平台采集图像信息丰富的优势，对测量结果进行多次优化，提高了测量精度.此外，在求解能量泛函时，使用贪心算法，保证了测量效率.

相比于三坐标测量方法，本文测量方法能够完整的重建管路模型，具有较高的测量精度，亦能获取充分的管路信息.该方法操作简单，测量效率高，不依赖操作人员经验，易实现操作流程的自动化.然而，蛇模型参数、测量平台布局、光照强度、参与重建相机数目等因素与测量结果的数学关系十分复杂，本文并未建立起一套明确的数学模型.探究各种参数与结果的关系，对提高测量精度和效率有重大意义，亦是将来需要进一步研究的内容.