圆盘水漂运动特性数值模拟研究

2021-08-11雷娟棉解文洋于勇刘奇

北京理工大学学报 2021年7期

雷娟棉，解文洋，于勇，刘奇

(北京理工大学宇航学院，北京 100081)

提要：为研究近水面的起飞再入式运动对飞行器近海面的高机动突防能力的影响,文中基于CFD数值模拟方法，湍流模型选取SST k-ω模型，利用重叠网格技术，将N～S方程与六自由度弹道方程耦合对三维空间内薄圆盘的水漂运动进行了数值模拟，研究了不同工况下水漂的入水特性和运动规律.结果表明：数值模拟计算得到的圆盘从接触水面到离开水面的时间与实验值吻合较好，圆盘的运动轨迹与实验结果相吻合；圆盘在打水漂向前运动的同时由于自身的旋转产生了马格努斯效应，从而使圆盘的运动轨迹产生了一定的侧向偏移以及圆盘自身的姿态发生了侧向偏转.

打水漂运动实际上包含了流体力学、刚体动力学和陀螺力学在内的众多力学问题，研究其运动规律需要考虑多方面的因素.对水漂运动的数值研究最早开始于法国里昂大学的Bocquet博士，其利用量纲分析的方法针对圆形和方形平板的水漂运动建立了数学模型，给出了水漂弹跳的条件以及在弹跳过程中能量的耗散规律[1].2004年，Christophe Clanet等[2]在Bocquet博士研究的基础上，利用高速摄影设备对圆盘弹跳实验进行研究，给出了圆盘的初始状态入水角度、入水速度、速度夹角和转速之间的规律，得出圆盘的理想入水角度约为20°的结论.2005年，Lionel Rosellini和Clanet等[3]进行了大量实验，分别对圆盘单次和多次弹跳下的运动规律进行了更加详细的研究，给出了圆盘水漂运动的数学模型和能量耗散模型，并利用实验结果进行了验证.邬明[4]应用 LS-DYNA 显式程序的ALE方法对圆盘击水弹跳运动进行了数值模拟仿真，探究了初始参数对圆盘击水弹跳的影响，验证了此数值模拟方法的可行性.但是作者在分析时缺少与实验结果的对比.赵坤[5]在研究水漂的水动力问题时，建立了水漂的六自由度动力学模型，并利用数值方法对水漂体的相关动力学特性进行了分析，通过与实验结果对比，验证了数学模型的可行性.2019年，孙士明等[6]设计了一种适宜滑跳的航行体构型，并利用CFD方法对模型重心位置的变化规律进行了数值模拟计算，最后基于设计的航行体构型进行了开放水面自由滑跳实验.通过观察结果，证明了将滑跳运动规律应用在飞行器上的可行性，运动过程中模型整体应保持光滑过渡.

近些年来，跨介质概念飞行器(一种既可以在空中高速巡航，同时又能在水中潜航的新型飞行器)在军事领域逐渐火热.当飞行器在近海面运动时，提高其机动性和隐蔽性对于发展此类飞行器至关重要.近年来，不断有学者提出利用打水漂这种起飞再入式的滑跳运动方式[6-10]，但是研究飞行器的滑跳运动资料目前来说非常少.打水漂作为一种常见的低速下固体击水滑跳运动，研究其运动对于发展跨介质飞行器的滑跳运动非常有借鉴意义.

目前国内对打水漂的研究起步较晚，且之前的研究多集中在对水漂入水的运动规律和流动机理研究上，还未形成完整的理论体系和研究方法，相关实验资料也同样很少.基于此，文中通过耦合求解雷诺平均的N～S方程与刚体的6自由度方程，利用重叠网格技术对三维空间内圆盘打水漂过程进行非定常数值模拟仿真，并通过与实验结果对比验证数值模拟方法的准确性，对圆盘在打水漂过程中的运动规律进行了分析.

1 数值模拟方法

1.1 流体控制方程

整个打水漂运动过程涉及到固、液、气多相的耦合问题，文中采用的流体为不可压缩流体，且无热交换，利用VOF模型来模拟由水、水蒸气和非凝结性气体的多相流场结构.计算过程中，VOF多相流模型将整个流场中的流体介质处理为单一流体介质，该介质均质且密度和黏度可变，根据同一单元内各相体积分数来区分不同的流体介质区域.

其中描述混合流场的连续性方程为

(1)

动量方程为

(2)

式中:i、j分别为1、2、3，表示不同的流体相；ui、uj为介质速度分量；μt为湍流黏性系数；ρm和μm分别为混合介质的密度和动力黏度，二者表达式分别为

(3)

(4)

式中,αi为不同流体相的体积分数，且满足α1+α2+α3=1.

1.2 物体运动方程

计算过程中采用惯性坐标系和体坐标系来描述圆盘的运动规律.其中惯性坐标系保持不变，体坐标系原点始终在圆盘质心位置，且固连在圆盘上.体坐标系为动坐标系，随圆盘的转动和平动而运动.体坐标系与惯性坐标系可以通过欧拉角相互转换.在打水漂过程中，圆盘在合外力的作用下做6自由度运动，根据运动的特点，可以将运动分为质心的平动和绕质心的转动.圆盘的平动在惯性坐标系下进行求解计算，根据动量定理有

(5)

式中：m为圆盘的质量；U为圆盘的平动速度；F为圆盘运动中所受的合外力.

关于圆盘的旋转运动，可以通过对惯性坐标系下的动量矩方程进行求解得出：

(6)

式中：ω为体坐标系相对于惯性坐标系的角速度；J为圆盘的转动惯量；M为圆盘在体坐标系下的力矩向量，通过对圆盘质心在惯性坐标系下的力矩MG进行计算得到

M=AMG.

(7)

其中A表示转动矩阵，

(8)

式中，φ、θ、ψ为圆盘的3个姿态角，即滚转角、俯仰角和偏航角.

在对圆盘的位置和姿态进行计算时，首先计算出圆盘某一时刻的受力以及力矩，再根据上面的动力学方程计算出圆盘此刻的加速度和角加速度，再通过积分运算计算出圆盘此刻的速度和角速度，最后得到圆盘下一时刻的质心位置和姿态角.

1.3 计算模型与边界条件

文中选择的计算模型为铝制圆盘，圆盘密度为水密度的2.7倍，圆盘半径R=0.025 m，厚度h=0.002 75 m.图1为三维空间下流场坐标系的示意图，坐标系的原点在圆盘质心，x轴向外为正；y轴为水平方向，向右为正；z轴为竖直方向，向上为正，文中重力沿z轴向下为负.

图1 流场三维坐标系示意图Fig.1 Schematic diagram of the three-dimensional coordinate system of the flow field

图2给出了zoy平面内圆盘的击水示意图.n和t分别为垂直圆盘和与圆盘表面相切的两个方向向量.s为圆盘浸入水中的长度，d为圆盘浸入水中的垂直深度.通过下面4个参数描述圆盘的入水状态：入射角α(圆盘平面与水平面的夹角)、速度夹角β(圆盘速度与水平面的夹角)、入水速度U和绕圆盘中心轴方向的转速Ω.

图3给出了yoz平面内计算域示意图，其中上面区域为空气域，下面区域为水域，两个区域的中间交界处为自由液面.计算域y方向长度为1.0 m，z方向高度为0.25 m，x方向宽度为0.4 m，设置水域高度为0.09 m，空气域高度为0.16 m，空气域的上侧边界条件设置为压力入口，压强与大气压一致；水域的下侧边界条件设置为压力出口.圆盘与计算域其余边界均设置为无滑移壁面.

图2 yoz平面圆盘击水示意图Fig.2 Schematic diagram of stone hitting water on the yoz plane

图3 计算域示意图Fig.3 Phase diagram of calculated domain

圆盘的运动规律由耦合了6自由度方程的非定常雷诺时均N～S方程求解圆盘的运动得出.物体假定为刚体，忽略表面张力，考虑重力的作用.湍流模型选取SST(shear stress transport)k-ω模型.压力场与速度场采用PISO耦合算法，时间上采用隐式格式，空间上均采用二阶迎风格式，时间步长设置为10-5，保证残差在每个时间步内迭代50次达到10-3.每个工况的总物理时间在1.5～2.5 s以内，保证一次弹跳的完整性[11].

1.4 重叠网格技术

由于圆盘的运动范围比较大，在进行非定常运动过程的数值模拟时，使用传统动网格方法在网格重构时会产生较大的网格变形从而给计算带来很大的误差.重叠网格方法(overset grids)是一种在处理运动边界时能够进行区域分割和网格组合的技术.按照网格生成的需要将复杂的流场分解开，在每个区域内生成高质量的网格块.其中区域与区域之间通过嵌套或重叠的方式来确定共享边界.共享区域(重叠区域)通过插值的方式来传递流场数据，而其余区域内部则用差分的方式传递流场数据.这一方式降低了网格生成的难度，提高了网格灵活性，保证了原始网格的质量，在模拟多相流运动问题时具有很大的优势[12-13].根据重叠网格技术的思路，将文中圆盘及其周围运动区域设置为部件网格，区域之外的流域设置为背景网格.

图4为yoz平面的重叠网格示意图，对网格进行重构处理过程中要保证总体网格的质量，从而减小插值带来的误差.由图4可知，重叠区域距离圆盘较远，网格大小适中，部件网格与背景网格重叠质量良好，符合重叠网格的要求.整个流场的总网格数量在275万左右，其中部件网格的网格量在25万左右，背景网格量在250万左右.考虑到圆盘在纵向平面内的位移变化较大，为了保证对气液交界面的捕捉精度，对平板及水面附近的网格区域进行局部加密.

图4 某剖面重叠网格示意图Fig.4 Schematic diagram of overset grid of a section

2 数值模拟结果与分析

2.1 数值模拟结果与实验结果对比分析

为了验证文中的数值方法在研究水漂运动时的可行性和准确性，文中选取文献[3]中的圆盘平板水漂实验进行算例验证.实验的圆盘材料、规格等参数与文中相同.根据实验，文中分别在工况1：初速度U=3.5 m/s、入射角α=20°、速度夹角β=20、圆盘旋转速度Ω=65 r/s和工况2：初速度U=5 m/s、入射角α=20°、速度夹角β=20、圆盘旋转速度Ω=65 r/s条件下对圆盘的弹跳规律和运动特性进行了数值模拟计算.

2.1.1运动特性对比分析

如图5展示工况1条件下圆盘进行水漂运动不同时刻的姿态变化.为了方便观察，所选切面为yoz平面内尺寸相同的部分流场，尺寸比例如图5(a)所示，每幅图像相隔时间均为6.5 ms，依次展示了圆盘从接触水面到出水整个过程.从图5中可以看出，初始时刻圆盘最低点与水面接触，在部分盘体进入水中后，圆盘周围产生一定的扰动，进而产生一定的凹陷.在整个过程中，圆盘以近乎恒定的入射角在水中滑行.在t≈32 ms时，圆盘离开水面到空中做抛物线运动.图6为展示了在xoy平面的部分流场圆盘与水面相互作用的空气体积分布云图.从图6中可以看出，在圆盘旋转的影响下，圆盘附近的水面同样产生了扰动，这个扰动随着圆盘的不断移动而向前移动.

图5 yoz平面不同时刻圆盘滑跳过程空气体积分数分布云图Fig.5 Cloud graph of air volume fraction distribution in the process of stone skipping at different moments on the yoz plane

图7为同一初始条件下圆盘进行水漂运动的实验图像，每幅图像同样相隔6.5 ms.通过对比图5和图7，能够看出数值模拟方法准确的模拟出整个水漂运动过程.同时从图5中可以看出，在整个打水漂过程中圆盘的入射角度几乎不变，这个规律与文献[2-3]中通过实验得出的结论是相吻合的.工况2条件下圆盘的运动规律图像与工况1类似，不再展示.

图6 xoy平面部分时刻圆盘滑跳过程中空气体积分数分布云图Fig.6 Cloud graph of air volume fraction distribution during stone skipping at some moments on the xoy plane

图7 不同时刻圆盘滑跳过程实验图像Fig.7 Experimental image of stone skipping process at different moments

2.1.2触水时间对比分析

根据陀螺效应，旋转的物体有维持自己方向稳定的趋势.在文中的研究中，旋转的作用是使圆盘在与水面接触过程中的角度保持稳定.而且旋转速度越大，圆盘越稳定，使之能够在较长的时间内与水面保持一个恒定的角度.当旋转速度低于能够保持圆盘稳定的阈值或圆盘无旋转时，圆盘将不能保持与水面恒定的角度，此时圆盘受力的方向不能够保持稳定，圆盘会侧翻进入水中，不能弹起来.

定义τ为圆盘从接触水面到离开水面所用的时间，即触水时间.在一定的范围内，随着圆盘初始转速的增大，触水时间τ值会逐渐减小，当转速增大到阈值后，τ值不再变化而是趋于一个固定值，此时圆盘的状态称为转速饱和状态，此时得到的触水时间值为τmin.文中选取的工况1和工况2转速都为65 r/s，处在转速饱和状态.

根据圆盘位移随时间变化的数值模拟结果和圆盘的尺寸数据，计算圆盘在两种工况下第一次弹跳过程的触水时间τmin.表1为两种工况下τmin的数值计算结果以及文献中实验结果.从表1中可以看出，在工况1条件下，τmin的数值模拟计算结果与实验结果相比，相对误差在0.5%以内；工况2条件下，τmin的数值模拟结果与实验结果相比相对误差不超过2%.可以看出数值模拟结果与实验结果的差距很小，这说明数值模拟方法能够较为准确地计算出圆盘最小触水时间.

表1 两种工况下圆盘触水时间τminTab.1 Time τmin under two operating conditions

通过以上结果可以看出，数值计算结果与实验结果具有较好的一致性，说明文中的数值计算方法在研究圆盘水漂运动时是可信的.

2.2 圆盘打水漂运动规律分析

下面将从3个坐标轴方向上圆盘的平移和转动规律入手来分析圆盘在打水漂过程中的运动特性.

2.2.1水平方向(y方向)

图8给出了工况1和2条件下圆盘的水平位移y和速度Uy随时间的变化规律(文中出现的圆盘的速度、位移和受力如无特殊说明，均指圆盘质心的速度、位移和受力).如图8所示，初始时刻，圆盘接触到水面，在水平方向上速度开始下降，之后变化逐渐减缓.从圆盘轨迹可以看出，圆盘在接触水面后水平方向上所受阻力突然增大，因而速度开始减小，入水后圆盘阻力变化范围很小，速度的变化幅度也降低.圆盘出水后在空中做抛物线运动，水平方向速度基本保持不变.数值模拟结果与实验结果的规律是相吻合的.

图8 工况1和工况2圆盘水平方向位移y与速度Uy随时间变化曲线Fig.8 Diagram of time-dependent displacement and speed Uy of the stone in the horizontal direction of Case 1&2

2.2.2竖直方向(z方向)

如图9分别给出了工况1和2条件下圆盘在竖直方向上的位移z以及速度Uz随时间的变化规律.从两幅图中可以看出，圆盘在初始时刻接触水面后，首先下降了一定的距离，到达轨迹最低点后，圆盘又开始逐渐上升.结合图5和图6进行分析，初始时刻圆盘在重力的作用开始下降，随着圆盘浸入水中的面积逐渐增大，根据升力公式：

(9)

图9 工况1和工况2圆盘竖直方向位移z与速度Uz随时间变化图Fig.9 Diagram of time-dependent displacement and speed Uz of the stone in the vertical direction of Case 1&2

(10)

随着触水面积的增大，圆盘所受的升力开始增大，直至图中最低点圆盘在竖直方向上速度衰减到零，此时圆盘所受升力大于重力.之后圆盘在二者合力的作用下，会发生反弹，直至离开水面.由于空气对圆盘的作用力很小，圆盘在空中做抛物线运动后再次进入水中，重新进行下一次滑跳运动直至能量不足不能再弹起.

2.2.3侧向(x方向)

前面两部分分析了不同初始条件下圆盘进行水漂运动时在水平方向(y方向)和竖直方向(z方向)的运动规律，这也是多数打水漂运动的相关实验和数值模拟研究主要关注的两个方向.文中在使用数值模拟方法对圆盘在三维空间内的水漂运动进行探究时，注意到圆盘在向前做水漂运动的同时，还存在明显的侧向(x负方向)运动，这也是在二维条件下研究水漂运动时观察不到的[14-15].通过数值模拟计算的工况1条件下圆盘的侧向位移随时间变化规律如图10所示；图11则为数值模拟计算得到的部分时刻下圆盘侧向力系数随时间变化的结果.由图10和图11可见，圆盘初始时刻侧向速度为0，且侧向力系数同样为0，所以此时的侧向位移变化非常小，入水后圆盘的侧向力系数开始急剧增大，较大的侧向力使得圆盘的侧向速度逐渐增大，在侧向上产生了明显的位移，之后圆盘的侧向力系数开始减小，直到出水时刻减小为0.侧向速度保持不变.图12给出了马格努斯效应示意图，圆盘在进入水中后，由于自身不断的旋转带动触水区域周围的水开始旋转，在圆盘两侧产生一个诱导速度场(U1、U2)，这个诱导速度场在水平方向上的分速度与来流作用下的附加速度场(Uw)相互影响，在自身旋转方向与来流速度方向相同的一侧，两个速度场相互叠加而增强，相反在另一侧两个速度场相互抵消而减弱.根据伯努利定理，圆盘两侧由于合速度的不同产生压力差，从而产生侧向力，即马格努斯力.马格努斯力与来流方向和圆盘旋转方向均垂直，使圆盘在侧向上产生了一定的偏移(Ur).

图10 工况1圆盘侧向位移随时间变化图Fig.10 Diagram of time-dependent displacement of the stone in the x direction of Case 1

图11 工况1圆盘部分时刻侧向力系数随时间变化图Fig.11 Diagram of time-dependent lateral force coefficient of the stone in a part of moment of Case 1

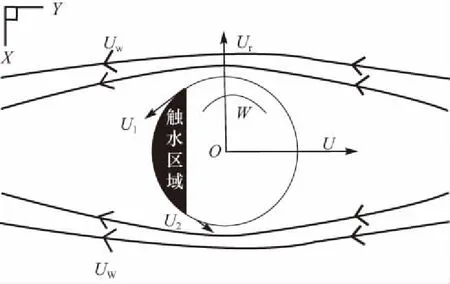
图12 马格努斯效应示意图Fig.12 Schematic diagram of the Magnus effect

除了前文提到的在侧向上圆盘的运动存在一定的偏移之外，观察到圆盘在运动过程中还存在一定的偏转.图13给出了初始时刻和出水时刻时，沿y轴负方向为观察角度的圆盘自身姿态变化.如图13所示，图中圆盘A侧方向表现为逐渐升高的趋势，而相反一侧则表现为下降的趋势.这表明圆盘在与水的相互作用下产生了一个旋转力矩.下面分析这个旋转力矩是怎么产生的.

图13 圆盘前后时刻偏转示意图Fig.13 Schematic diagram of the deflection of the stone

前文提到圆盘由于自身的旋转，使得圆盘触水区域周围的水产生了诱导速度场，这个速度场在圆盘的两侧表现为相反的方向.由于圆盘初始状态下与水平面存在一定的角度，因此圆盘两侧的诱导速度U1可以分为水平分速度U1y和竖直分速度U1z，其中竖直分速度U1z在图中AC两侧的方向是相反的.在A点一侧这个分速度方向为竖直向上，另一侧则为竖直向下.这两个相反方向的速度，作用在圆盘上，在圆盘两侧产生了使圆盘发生转动的力矩.

下面分析圆盘在单次打水漂运动中的能量损失，在文中，圆盘的能量为其自身的机械能，由动能和势能两部分组成：

(11)

式中:E为圆盘的机械能;m为圆盘质量;g为重力加速度(文中取9.8 m/s2);h为圆盘相对水面的高度，初始时刻h=0 m，离开水面时h同样为0 m.

通过数值模拟计算得到两个工况下圆盘单次水漂运动的相对能量损失结果.工况1下圆盘的相对能量损失为39.75%,工况2下圆盘的相对能量损失为36.39%.因为工况2条件下圆盘初始速度较大，圆盘在水中的时间相对更短，消耗的机械能较少,比工况1能量损失小.