基于动态贝叶斯网络的燃气管网燃爆风险分析

陈军，兀亚伟，李垣志，钱新明，袁梦琦

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

提 要:针对传统风险分析方法无法实现动态评估的局限性，提出了基于动态贝叶斯网络的燃气管网风险分析模型. 基于管道失效原因与事故后果，构建了事故演变全过程网络结构，并运用马尔科夫理论将演变全过程与时间相关联，最终建立了动态贝叶斯风险分析模型. 该模型基于贝叶斯理论进行泄漏、致灾模式及后果节点的概率计算，实现了对燃气管网事故的原因诊断及事故发展态势预测. 以松原“7.4”燃气爆炸事故为例，应用本模型演示了燃气管网事故推演技术，结果表明：事故是由第三方施工破坏引发燃气泄漏，由于燃气在土壤中的扩散范围不断扩大，扩散范围内受限空间数量不断增加，人员活动情况也更加复杂，进而增大了燃气聚集与点火概率；结合事故现场条件，本模型对这起爆炸概率进行了推演，认为此次燃气爆炸概率将在泄漏60 min后达到42.3%,高于安全泄放概率；该结果与真实情况基本相符，进一步验证了模型的可行性与可靠性.

燃气管道是城市生命线的重要组成部分，受自然灾害、市政施工等多因素影响，管网事故频发[1]. 埋地燃气管道与其他市政管线纵横交错，一旦发生泄漏，管网本身的隐蔽性与复杂性、天然气的易燃易爆性以及城市人口活动等不确定的风险因素在时间空间上的耦合作用，使得燃气管道泄漏极易演变为燃爆事故，造成大量人员伤亡及经济损失. 以台湾高雄“8.1”燃气爆炸为典型事故案例，在长达3 h的泄漏过程中，燃气经由排水管线扩散至周边3 km2的区域，而指挥中心错误的处置措施并没有降低风险，最终燃气泄漏演变为连环爆炸，造成33人死亡，321人受伤，同时损坏多条重要道路及大量周边建筑. 因此，有必要对燃气管网进行风险分析. 风险分析可以识别燃气管网的薄弱环节，预测燃气燃爆事故的可能性及其整体影响，据此有针对性地制定风险控制措施，实现消除或降低燃气风险的目标[2].

风险分析被定义为事故概率和后果的数学函数[3]. 对于燃气管道，概率评估侧重于分析管道泄漏概率. 后果分析则研究对人体有害事故的物理影响，包括喷射火、火球燃烧和蒸汽云爆炸(vapor cloud explosion,VCE)等，综合管网失效可能性及后果的分析可以定量得到燃气管网的风险. 然而，从燃气管道泄漏到不同致灾模式(喷射火、VCE等)之间还存在着一个演变过程. 有研究表明，致灾模式基于管道故障模式、气体泄漏与燃气气云着火的时间间隔以及周围空间的限制程度，与这些事件相关因素的组合导致了最终致灾模式[4]. 由于这些因素充满了不确定性，各致灾模式的概率一般基于历史数据得到. 根据API RP581的历史数据显示，管道泄漏后发生安全泄放、喷射火、蒸气云爆炸以及火球的概率分别为0.8、0.1、0.06和0.04[5]. 利用历史统计结果而不考虑致灾模式的发生条件显然难以得到可靠的结果. 此外，传统的风险分析方法(故障树、事件树等)在燃气管网风险评估应用中存在一些局限性：故障树和事件树可以定性分析燃气事故的原因及失效后果，并定量确定相应的概率，但是它们所固有的静态结构无法适应事故的动态演化过程[6-8]. 例如，当燃气管网泄漏后，随着泄漏时间的增加和扩散范围的扩大，范围内地下空间数量及人流密度也随之变化，直接影响了燃气的聚集概率与点火概率，最终导致燃气的燃爆概率的改变. 由此可以看出，燃气泄漏的动态演化过程在故障树和事件树中难以被准确描述.

贝叶斯网络(Bayesian network,BN)与传统的风险分析方法有所不同，它是表示概率系统中不确定知识的一种很好的因果分析工具，可以定量表示事件节点间的因果关系，对事故的前因后果做出推断，还能对新得到的信息进行处理实现概率更新[9]. 动态贝叶斯网络(dynamic Bayesian network,DBN)是静态贝叶斯网络在时间序列上的展开，考虑了时间因素对模型的影响，适用于描述性能波动的动态系统，例如，描述灾难的演变过程[10]. 目前利用DBN研究燃气管网事故演变过程的文献很少. QIU等[11]曾将蝴蝶结模型与动态贝叶斯网络结合用于分析燃气管网风险，实现了时变条件下的事故跟踪和演化推理. 然而，该方法在实践应用中，难以准确获取节点事件的实时信息，并且在描述多变量系统突变过程的准确性方面存在局限性.

DBN的一个关键挑战在于将转移概率定义为父节点随时间变化的状态值[12]，从而实现预测推理系统状态的功能. 马尔可夫链理论作为运筹学中的一种有效预测方法，所需数据少，并且随着原始数据的增加，预测的准确度会越来越高，在管道腐蚀、剩余寿命预测模型方面都有成功应用的案例[13-14]. 运用马尔科夫链理论建立马尔科夫模型可得到状态转移概率矩阵，以此可解决DBN转移概率获取困难的问题，相继也能够解决燃气演变态势不明确的问题，对燃气演变过程做出准确的预测.

本文基于动态贝叶斯网络建立了燃气管网风险分析模型. 重点分析了燃气管网事故从失效原因到后果的演变过程，并运用马尔科夫模型将燃气事故演变过程与时间相关联，以此构建的燃气管网DBN风险分析模型，实现对燃气事故原因的快速诊断以及对管网未来风险态势预测，同时评估了应急响应对于燃气事故的控制效果，为应急决策提供理论参考.

1 风险分析方法

1.1 动态贝叶斯网络

DBN是静态贝叶斯网络的扩展，可以容纳时间序列数据，适用于对动态系统进行建模. DBN由一系列时间片和时间链路组成，每个切片代表一个静态贝叶斯网络，描述相应时间步中的变量，而不同时间切片中变量之间的时间链接表示时间概率依赖[15]. DBN作为数据分析和不确定性推理的工具，帮助人们将概率统计应用于复杂领域，并已被应用于各种安全评估和风险分析问题[16-18]. 通常，DBN有以下假设[12]：

① 稳定性. 对于所有t，转移概率PB(X[t+1]|X[t])总是相同的.

② 马尔可夫性. 下一时间片中节点的状态仅与当前时间片中的状态相关，与前一状态无关.

满足上述两个条件的DBN可以表示为(B1，B→)，其中B1是先验网络，也称为初始网络，B→称为“2片时间贝叶斯网络”(2TBN)或转移网络[19]. 图1显示了初始网络、2TBN和DBN. 从X[t]到X[t+1]的转移概率为PB(X[t+1]|X[t]). DBN的联合概率分布用以下公式表示为

P(X[1],X[2],…,X[t])=

(1)

式中X[t]为节点X在t时刻的状态.

图1 初始网络、转移网络和动态贝叶斯网络Fig.1 Initial network,transition network and dynamic Bayesian network

DBN是一个隐马尔科夫模型，符合一阶马尔科夫假设，DBN节点的转移过程符合马尔科夫过程[20]. 因此，动态贝叶斯的转移概率可以基于马尔科夫模型得到，

PB(Xj[t+1]|Xi[t])=zi,j/zi

(2)

式中：PB(Xj[t+1]|X[t]为已知X[t]=i的条件下，X[t+1]=j的转移概率；zi为X节点处于状态i的个数；zi,j为节点X由状态i转为j的个数.

1.2 证据理论

条件概率表(conditional probability table,CPT)用于确定DBN中节点之间的定量关系,它的建立有两种方式：机器学习和专家知识构建. 由于缺乏大量事故演变过程具体数据，因此选择专家知识来构建CPT. 本文将Dempster-Shafer证据理论用于处理专家知识. 与概率论相比，证据理论更善于表达和处理不确定性，并提供了一种融合不同信息源的不同数据的组合规则. 证据理论已被用于许多领域进行风险评估和专家决策[21-22]. 下面将简要描述该理论[23-24].

设Θ是一个识别框架，在识别框架Θ上的基本概率赋值是一个2Θ→[0,1]的函数m，称为mass函数. 并且满足

(3)

对于∀A⊆Θ，识别框架Θ上的有限个mass函数m1，m2…，mn的Dempster合成规则为

m(A)=

(4)

式中K为归一化常数：

(5)

1.3 动态贝叶斯推理

无论是静态BN还是DBN，推理的依据均是贝叶斯公式

(6)

相较于静态BN，DBN还可以进行预测推理. 根据当前观测的所有信息及历史数据，预测未来时刻系统的状态. 根据贝叶斯理论，节点在时间t的概率由所有父节点的组合确定. 使用式(7)计算P(T|X1,X2,…,Xn)表示的(T|X1,X2,…,Xn)的概率分布为

P(T[t])=P(T[t]|Xi[t])P(Xi[t])+…+P(T[t]|Xn[t])P(Xn[t])

(7)

2 燃气管网DBN风险分析模型

2.1 动态贝叶斯网络节点

本文在对大量的燃气管网事故研究分析的基础上，结合专家经验及前人研究，提出了可以清晰描述燃气管网事故演变全过程的基本节点. 由于篇幅所限，仅对部分节点选取及划分进行详细描述，其他节点可参考文献[9,25]. 燃气管线事故的部分DBN节点(节点g～j)描述如下.

节点g:致灾模式. 城市燃气管道泄漏之后开始向四周扩散，当存在受限空间和点火条件时会发生受限空间蒸气云爆炸(confined vapor cloud explosion,CVCE)；若周围没有受限空间只有点火条件时会发生喷射火、闪火以及无约束蒸气云爆炸(unconfined vapor cloud explosion,UVCE)；若二者都不存在，则燃气得以安全泄放[4]. 对于UVCE，它的形成条件较为苛刻，发生概率极低，一般不考虑[26]. 依据以上分析，将致灾模式可以分为CVCE、火灾和安全泄放三种.

节点h:地下空间分布. 通过对多起燃气管网事故的统计分析，燃气泄漏之后的爆炸事故大多数为地下空间爆炸[27]. 地下空间包括供热井、排水管线及电缆沟等，当城市地下燃气管网泄漏气体通过土壤扩散至这些相邻空间时存在爆炸的可能. 地下空间分布会影响到燃气聚集概率进而影响发生爆炸的概率. 除此以外，地下空间大多数是生命线附属设施或生命线本身，它们的分布也会导致燃气事故对生命线供应产生不同影响. 综合考虑以上因素并根据实际调研结果，选取燃气扩散范围内存在1个及以下,2、3个及以上个地下空间三种状态.

节点i:受威胁人员. 受威胁人员指受到燃气事故威胁的人员. 受威胁人员会影响燃气燃爆的点火概率. 文献[28]中给出了不同点火源的点火概率，在城市中，主要点火源为人口活动引起，因此将模型简化，点火概率由受威胁人员数量来表征. 除此以外，受威胁人员也会影响燃气事故的伤亡人数. 综合考虑两者影响，选取小于50人、50～100人、大于100人三个等级.

节点j:应急响应. 应急响应对于灾害控制、减小事故后果很有意义. 快速有效的应急响应不仅能控制燃气泄漏后的事故演化发展，防止发生火灾或爆炸，而且也能控制灾后事故后果，有效降低燃气泄漏致灾风险. 在本文中，为检验应急响应对于控制致灾模式及事故后果的能力，将应急响应定性分为两种状态：有效应对与反应不力. 前者有助于致灾模式及后果的控制，后者对于致灾模式及后果控制没有帮助.

表1给出了燃气管网事故全过程的DBN节点及其分类. 通过对燃气管网事故研究、文献调研以及咨询专家，定义了网络节点，确定了节点间的因果关系，建立起燃气管网事故全过程的先验网络结构，如图2所示.

表1 DBN节点状态划分Tab.1 Classified states of DBN nodes

图2 燃气管网事故贝叶斯网络Fig.2 Bayesian network of a gas pipeline network accident

2.2 条件概率表

为了对贝叶斯网络节点间建立定量的联系，需要收集各节点的条件概率分布. 本研究邀请了5位经验丰富的专家填写问卷来收集节点的条件概率，5位专家的具体信息见表2. 利用D-S证据理论对专家知识进行信息融合及处理，提高问卷的一致性和可信度[9].

以“人员伤亡”为例，条件概率取决于灾害类型、受威胁人员以及应急响应三个节点，在收集完问卷后，专家评分如表3所示. 由于篇幅限制，表3仅列出受威胁人员在50人以下情况下的人员伤亡分布情况.

在表3中，m1～m5是5位专家对于人员伤亡三种等级概率的判断.m1(1，2，3)是第一位专家给出人员伤亡的条件概率分布，(1.00，0.00，0.00)表示专家认为在燃气安全泄放且应急救援有效的情况下，伤亡人数应小于3人. 最后一列为利用证据理论对所有专家评分计算得到的最终得分，即人员伤亡的条件概率分布.

表2 专家具体信息Tab.2 Specific information of experts

表3 人员伤亡条件概率分布Tab.3 Conditional probability distribution of casualties

2.3 转移概率

在已建立的燃气事故贝叶斯网络中，点火及聚集概率会由于燃气扩散范围的增大而发生变化，为点火和聚集节点建立状态转移概率表，可以预测燃气事故随时间推移的风险演变. 燃气泄漏之后在大气或土壤中进行扩散，由于燃气浮力特性影响，一般在大气中无法向四周扩散很远. 而对于燃气在土壤中扩散，具有一定的隐蔽性，难以被发现，可以扩散至很远的地方. 因此本文以燃气在土壤中扩散范围作为燃气扩散的范围进行研究. 燃气扩散距离随着扩散时间增大而增大，并且两者近似呈幂指数关系，如式(8)所示[29]为

R=αTβ

(8)

式中：R为距泄漏口的距离；T为燃气扩散时间；α和β是与燃气泄漏泄漏量以及土壤性质等因素有关的系数. 根据现有研究实验，扩散距离总存在一个最小值Rmin和最大值Rmax，假设燃气泄漏事故演变过程在n个时间片内完成，每个时间片为Δt，利用这些已知条件即可拟合出燃气扩散范围与扩散时间关系的规律曲线.

以燃气聚集为例说明建立转移概率表的过程. 根据相关部门提供的地下管网分布图，可以得到地下空间具体位置，结合燃气扩散规律，建立的地下空间分布状态概率转移表如表4.

表4 状态转移条件概率表Tab.4 Conditional probability table of state transition

在完成转移概率表的输入后，燃气管网DBN风险分析模型建立完成，在此基础上可以实现燃气管网的失效概率计算和风险演变预测. 本文利用目前应用最广泛的贝叶斯网络开发软件之一Genie软件[30-31]，对燃气管网事故全过程进行风险分析.

3 实例分析

3.1 背景介绍

以松原市“7.4”燃气爆炸事故为例进行风险分析. 2017年7月4日13时23分许，某施工队在实施旋喷桩基坑支护施工时，旋喷桩机将燃气管道钻漏，泄漏气体经多渠道泄漏至周边医院. 14时51分，燃气遇不明点火源发生爆炸. 根据事故统计，事故共7人死亡，重伤13人，轻伤72人，并且造成包括医院等多所建筑物严重破坏. 爆炸事故具体时间线如图3所示.

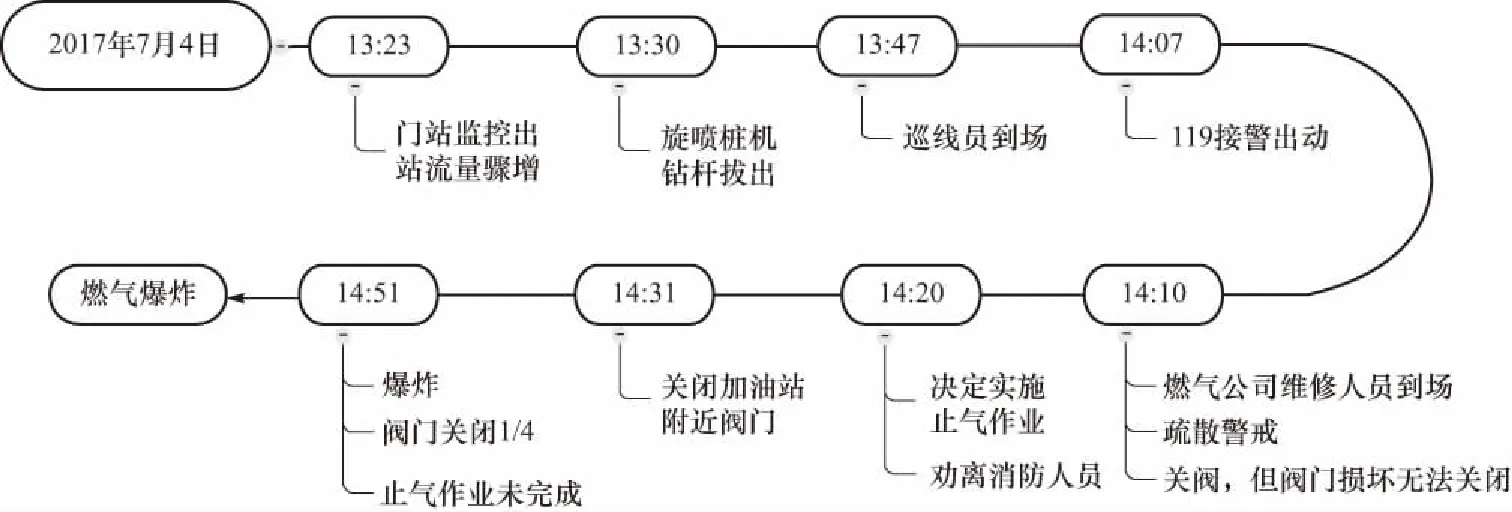
图3 松原“7.4”燃气爆炸事故时间线Fig.3 Timeline of the Songyuan “7.4” gas explosion accident

3.2 事故原因诊断

诊断推理的目的是为了判断管道失效原因，以便及时进行紧急救援. 利用建立的DBN模型对这起事故进行诊断推理，推理结果如表5所示. 第三方破坏的后验概率明显大于其他因素的后验概率，由此可以推断，燃气管道失效原因很可能就是由于第三方破坏所引起. 事故调查结果显示，燃气管线破裂是由于第三方公司在燃气管道安全间距范围内盲目进行钻孔打桩作业而导致，推理结果与实际结果一致.

表5 失效原因后验概率更新Tab.5 Posterior probability update of cause of failure

3.3 事故演变预测

将这次事故所确定的信息输入到DBN进行初始化设置，设置的节点如表6所示. 假设风险演变往往发生在7个时间片内，每个时间片为15 min. 设置完成后，用于风险预测的燃气管网DBN风险分析模型如图4所示. DBN模型展示了在不同时间片内包括风险在内的多个节点概率变化.

表6 节点初始设置Tab.6 The initial setup of nodes

图5所示曲线说明了随时间推移的致灾模式状态变化. 在管道泄漏初期，燃气安全泄放的概率为

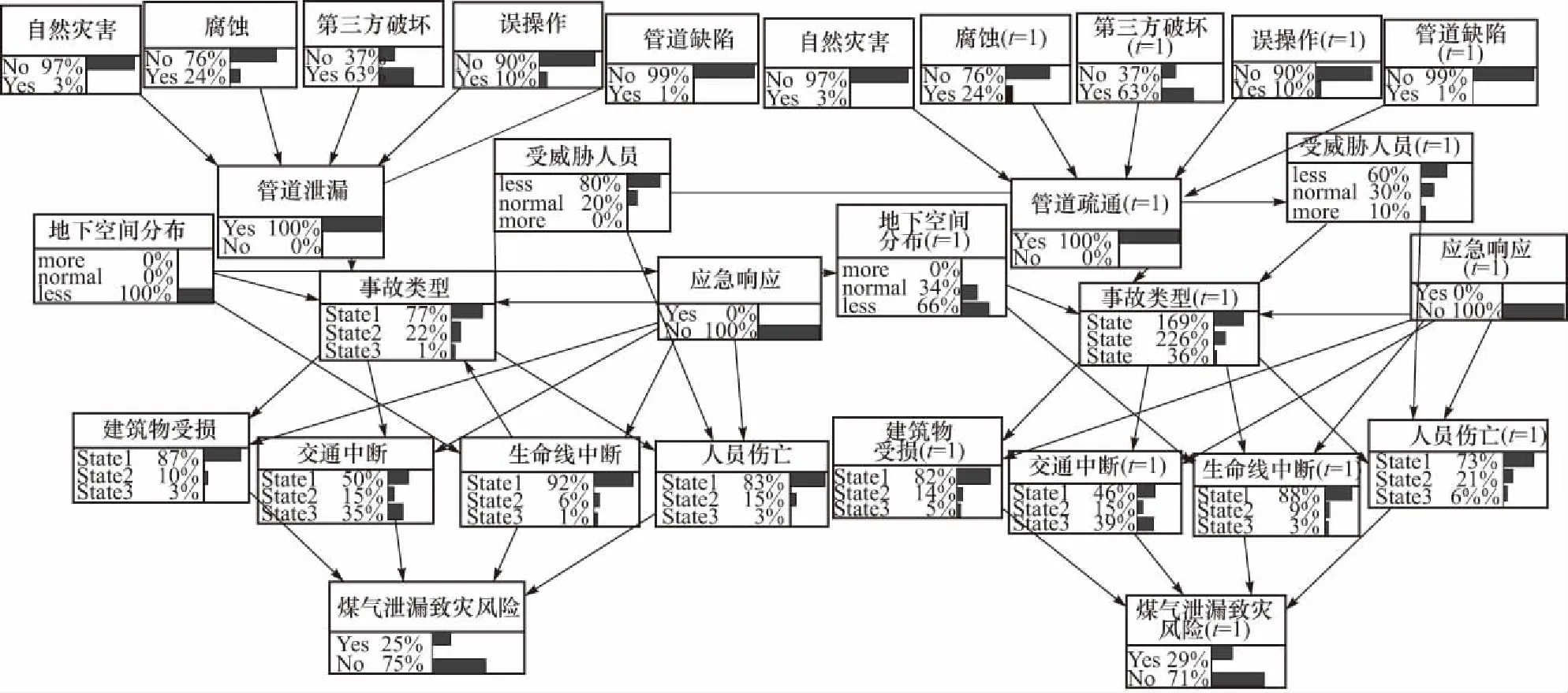
图4 燃气管道泄漏事故演变动态贝叶斯模型Fig.4 The DBN model of leakage accident evolution in the gas pipeline

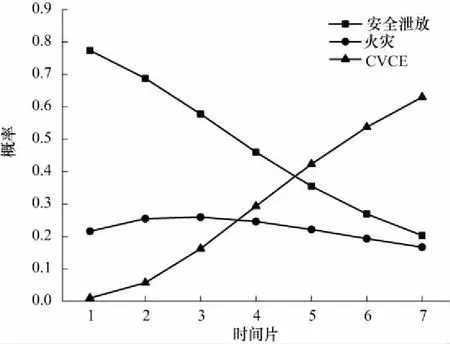
图5 致灾模式概率变化Fig.5 Probability change of accident type

77.4%，火灾的几率为21.6%，这是由于管道被第三方施工所破坏，机械设备作业时容易出现撞击火花，致使点火概率较高，而燃气泄漏后被立即点火会出现喷射火. 随着时间的推移，燃气扩散范围增大，受到事故威胁的人员数量快速增加，因此火灾概率在事故初期逐渐升高；同时燃气在扩散过程中，出现在受限空间并处于爆炸极限的概率也在缓慢增加，因此火灾概率之后又减小，而发生爆炸的几率持续增大. 高雄燃气管道泄漏爆炸也是类似这样的过程. 特别地，在第5个时间片即60 min后，燃气爆炸的几率已经达到了42.3%，超过了燃气安全泄放(35.5%)和火灾(22.1%)的概率，这意味着在此之后很有可能发生爆炸事故. 在实际事故中，燃气爆炸发生于泄漏后88 min，处于推理的第7个时间片，此时DBN预测的后果如表7所示. 除建筑物受损节点外，其他节点推理结果和实际情况相符，验证了该方法的可行性.

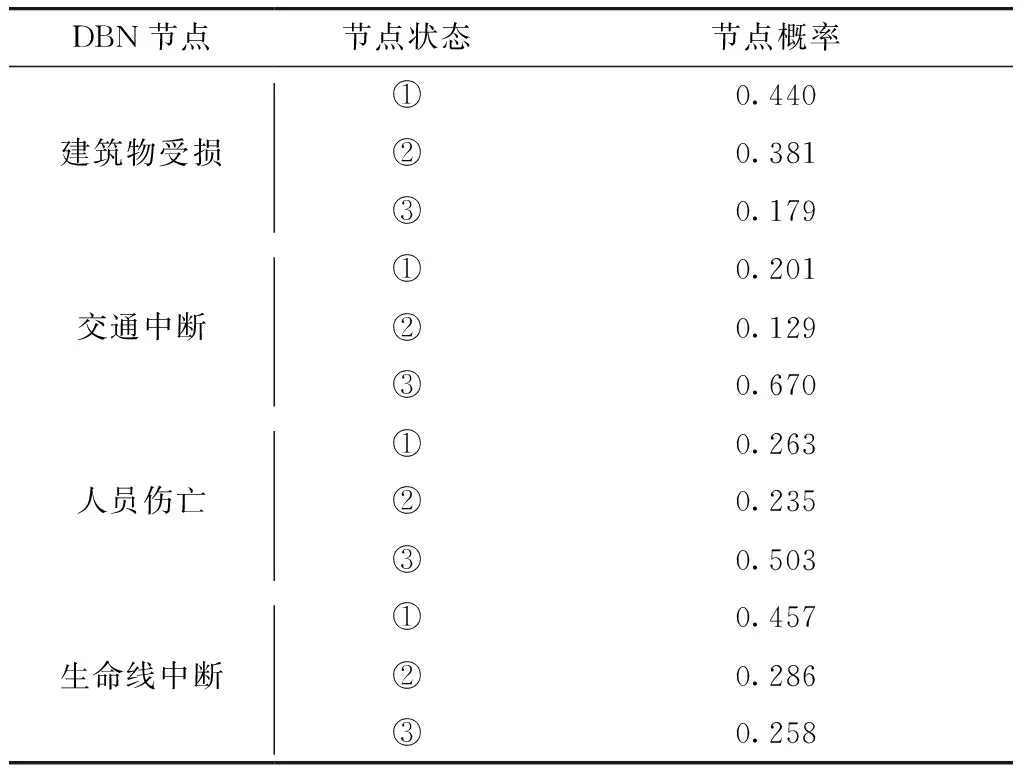
表7 后果节点状态概率在第7个时间片

3.4 应急响应分析

在这次事故中，操作人员将旋喷桩机钻杆拔出、燃气公司人员止气作业操作慢以及劝离消防人员等几次应急决策失误，致使发生燃气爆炸并造成了严重的后果. 为了比较应急响应对事故控制的效果，仍然对这次泄漏事故进行分析，并将应急响应设置为不同时间生效进行对比，对比结果如图6和图7所示.

如图6所示，在第5个时间切片中，发生爆炸可能性为最大，而在有效应急响应的情况下，第5个时间切片倾向于燃气安全泄放. 在随后的时间中，应急响应主要是针对灾害后果的控制，如表8所示，与同一时间段没有介入应急响应的结果相比，4个后果节点出现最严重情况的概率明显降低，并且较早的应急响应时间可以控制事故，防止出现严重后果.

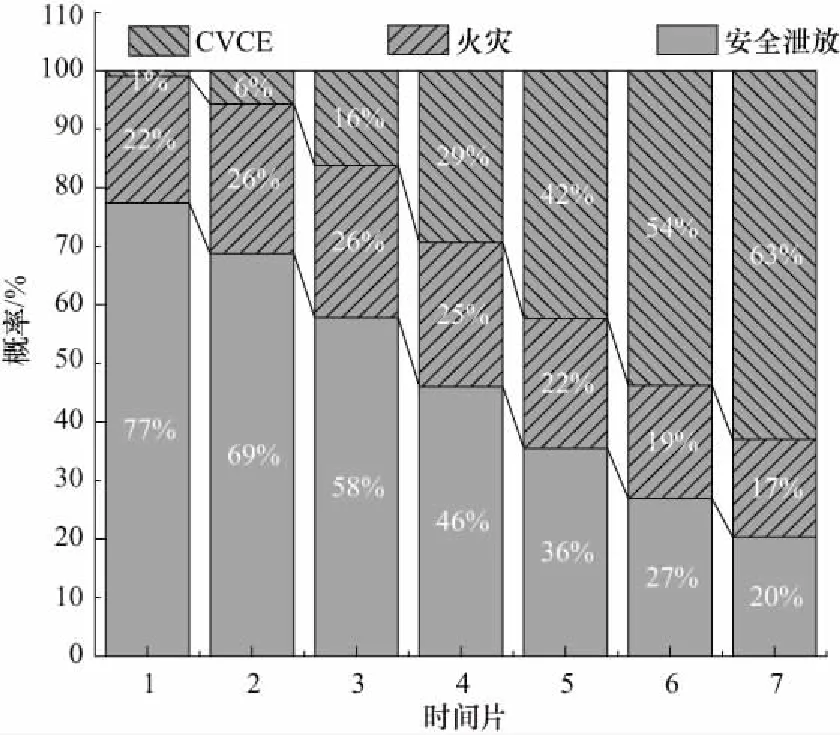
图6 应急响应无效时致灾模式演变Fig.6 Evolution of accident types without emergency response

图7 应急响应有效时致灾模式演变Fig.7 Evolution of accident types with emergency response

根据DBN分析结果，可以为应急决策提供有效理论支持. 在本文中，仅对应急响应的重要性以及介入时间进行了说明验证，对于具体的燃气管道，利用动态贝叶斯网络模型对燃气管道事故进行推演，结合实际情况采取相应的应急救援措施. 后期可以对应急响应节点进行拓展，这些节点的完善可以为应急响应系统提供更多的技术支持.

表8 应急响应不同响应时间其他节点概率变化Tab.8 Probability changes of other nodes under different emergency response times and states

4 结 论

① 分析了燃气管网事故演变过程，获得燃气事故演变的关键节点，依据证据理论处理专家知识确定节点间的定量关系形成贝叶斯网络结构，在此基础上运用马尔科夫链理论将事故演变过程与时间相关联，最终建立了燃气管网DBN风险分析模型.

② 对松原“7.4”燃气爆炸事故分析，DBN模型能够准确地推断出泄漏是由于第三方破坏所导致，并预测燃气爆炸在泄漏60 min之后，对于事故后果的预测也与实际基本相符，证明了该模型的可靠性.

③ 燃气管网DBN风险分析模型为燃气管网动态风险分析提供了新思路，同时还为应急响应机制建立和高效协调利用应急资源提供理论依据，最大限度地减少或控制燃气事件的发生和影响.

下一步的研究将集中在以下三个方面：①利用专家知识得到节点间的条件概率分布，不可避免带有一定的主观性，应结合更多燃气事故案例计算节点的条件概率表. ②在动态贝叶斯网络节点中融入物理损伤模型(泄漏量模型、喷射火模型等)能够进一步提高DBN的可靠性与准确性，然而相关参数的录入导致DBN难以在实际中应用. 因此，如何在确保预测准确性的同时降低模型复杂度需要进一步研究. ③扩展应急响应节点，节点完善可以为应急决策提供更多的技术支持.