双定子高温超导电机阻尼绕组对超导励磁磁场及电枢反应磁场作用机理分析*

王 睿， 王玉彬， 朱新凯

[1.中国石油大学(华东)新能源学院，山东 青岛 266580；

2.东南大学 电气工程学院， 江苏 南京 210096]

0 引 言

近年来，随着直驱风力发电技术的快速发展，对发电机的功率密度以及容量等级要求越来越高。传统直驱发电机因其体积和重量过大，限制了风力发电技术的进一步发展。与传统直驱发电机相比，超导直驱发电机则因具有体积和重量小、结构紧凑、功率密度和效率高、稳定性好等优点[1-2]，受到广泛关注。与低温超导电机(LTSM)相比，高温超导电机(HTSM)的制冷系统技术难度及所需制冷量大大降低，得到了快速发展[3-4]。得益于超导线材的高通流能力，HTSM的励磁绕组部分采用超导励磁绕组[5]取代常规永磁体或铜质励磁绕组，较少匝数的超导励磁线圈即可产生强气隙磁场，使大容量HTSM体积和质量大大减小。因此，HTSM在直驱风力发电、船舶电力推进以及航天发射等领域具有潜在的应用前景。

超导线材维持超导性必须同时满足临界电流Jc、临界温度Tc以及临界磁场Hc[6]3个临界条件。当超导线材放置在低温冷却介质中，如(77 K)的液氮环境下，可以满足其对临界温度的要求。但当超导(SC)线圈位于磁场环境复杂的电机系统中时，磁力线一旦沿铁心进入励磁磁场环境,很容易影响超导励磁线圈的超导特性，导致其脱离超导状态[7]。因此，研究HTSM中SC线圈周围的磁场变化对超导线材临界电流的影响，对预防超导励磁线圈失超具有一定借鉴价值。

为减弱磁场对SC线圈的影响，降低超导励磁线圈的失超风险，超导电机内部一般会采用电磁屏蔽层。文献[8]结合HTSM的特性，针对单一屏筒式阻尼屏蔽系统的弊端，提出了多屏筒式阻尼屏蔽系统。文献[9]则利用鼠笼式阻尼导条的涡流特性，针对DS-HTSM，提出鼠笼式阻尼导条与铜屏蔽层相结合的方法。虽然这种组合式电磁屏蔽方案有效地减弱了交变磁场可能引起的SC线圈失超风险，但是其具体的作用机理并未进行深入的理论分析，值得进一步研究。

鉴于此，本文建立了DS-HTSM的静止气隙磁导模型，通过解析方法分析阻尼绕组对SC线圈交变磁场的影响，并应用有限元验证所提分析方法的正确性。

1 DS-HTSM结构及工作原理

图1为DS-HTSM结构的平面示意图。为便于实现励磁绕组的静态密封[9]，DS-HTSM采用双定子结构配置。其中，励磁绕组放置在内定子的冷却杜瓦中，电枢绕组放置在外定子上，转子则由调磁块和非调磁块间隔排列组成。同时，类似于内定子极靴的导磁环还可为电枢磁反应场提供切向磁路，从而降低电枢反应磁场对超导励磁绕组临界电流的影响。

图1 DS-HTSM结构图

参考文献[10]，DS-HTSM基于气隙磁场调制工作原理实现机电能量转换。励磁磁场经调磁环转子调制出的有效谐波磁场极对数与电枢反应磁场极对数相对应，且内定子极对数Pin、外定子极对数Pout和转子极数Nr之间满足式(1)：

Pout=|Pin-Nr|

(1)

同时，电枢谐波磁场的转速Ωa与转子转速Ωr之间满足式(2)：

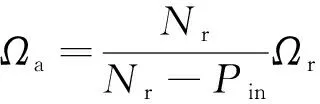
(2)

在合理的内外定子极对数配合下，DS-HTSM可以实现低速直驱功能。

2 内气隙磁场解析

对于超导励磁绕组置于内定子侧的DS-HTSM而言，内气隙磁场和SC线圈直接作用，因此本文主要针对内气隙的磁通密度进行分析。图2所示是带有鼠笼式阻尼绕组的DS-HTSM结构。

图2 带有阻尼导条的DS-HTSM结构配置

通常，负载运行工况下，DS-HTSM气隙中同时存在励磁磁场和电枢反应磁场，因此在研究鼠笼式阻尼导条对SC线圈周围谐波的影响时，要分别对这2种磁场加以考虑。为了方便定性分析阻尼绕组的作用，对电机结构模型作出如下假设：

(1) 内外定子铁心和调磁块的磁导无限大，忽略磁饱和影响；

(2) 忽略端部效应及磁极叠片中涡流效应的影响；

(3) 由于阻尼导条的半径较小，且放置在闭口槽中，暂不考虑阻尼导体漏阻抗的影响；

(4) 阻尼导条中电流沿轴向均匀分布。

2.1 磁导解析式

基于磁场调制原理，根据双定子类电机的励磁磁动势、电枢磁动势、调磁环转子磁导、外定子磁导及内定子磁导分布，同时借助傅里叶分解，可以分别得到励磁磁场和电枢反应磁场经调制后产生的内气隙磁通密度分布[11]。

图3所示为调磁环转子磁导波形。

图3 调磁环转子磁导波形

可得调磁环转子磁导λr(θ,t)(不计非调磁块通过的少量磁通)如下：

(3)

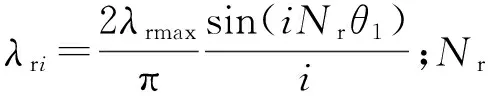
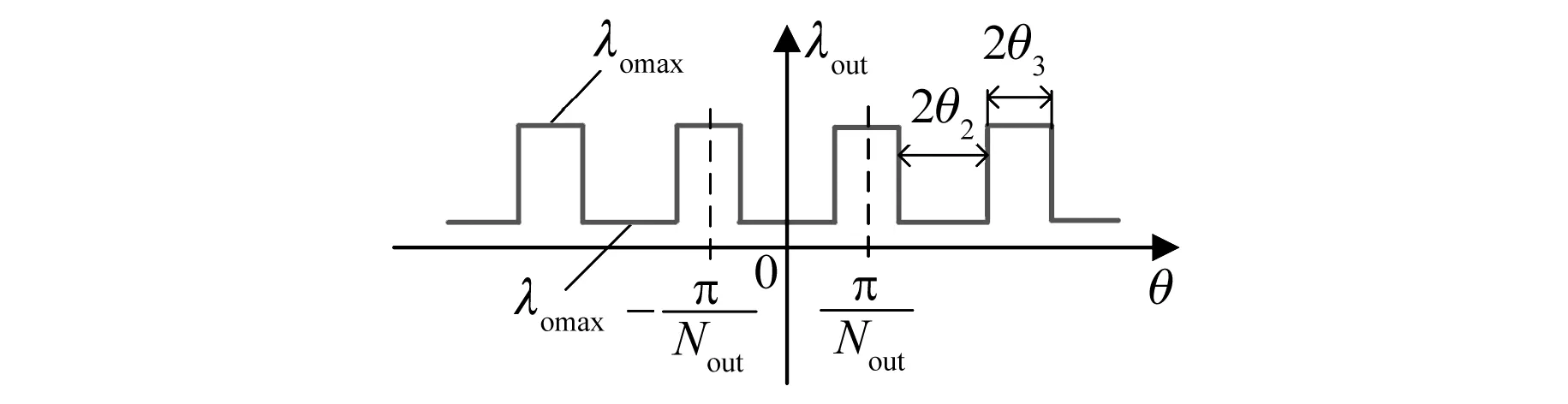
图4 外定子磁导波形

磁导λout(θ)表达式为

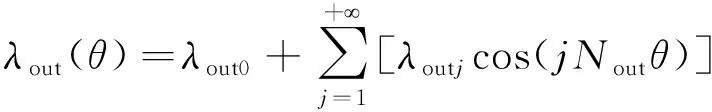
(4)

图5所示为DS-HTSM电机内定子磁导λin(θ)的分布波形。

图5 内定子磁导波形

λin(θ)表达式为

(5)

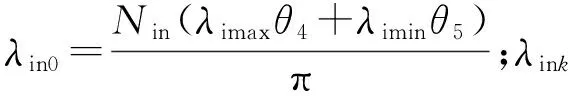
2.2 励磁磁场产生的内气隙磁密

励磁磁场产生的内气隙磁密是指当电机空载运行时，仅励磁磁场作用，励磁磁动势经调磁环转子以及内定子齿共同调制，在内气隙中调制产生的气隙磁密。图6所示为励磁磁动势波形(计及内定子齿的作用)。

根据图6可以得到空载时DS-HTSM的励磁磁动势ff(θ)：

(6)

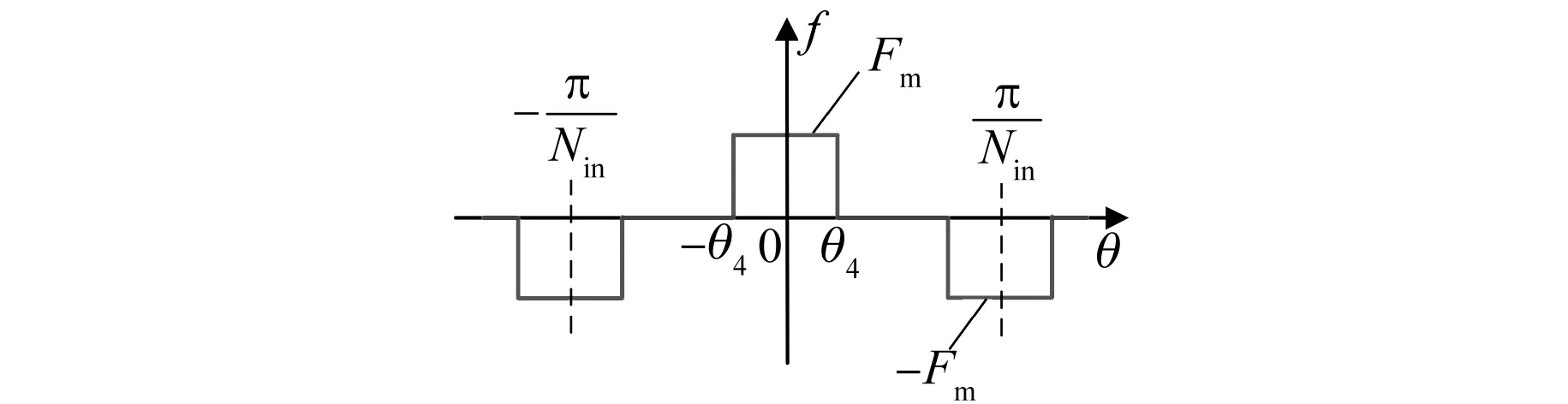
图6 励磁磁动势波形

图7所示的励磁磁场磁路，主要包括穿过内外气隙的闭合磁路及直接经导磁环闭合的回路两部分，其中，前者是重点研究内容。

图7 励磁磁场磁路图

结合式(3)和式(6)可以得到励磁磁动势经由调磁环转子调制而产生的内气隙磁密Binf(θ,t)：

Binf(θ,t)=ff(θ)·λr(θ,t)=

(7)

2.3 电枢反应磁场产生的内气隙磁密

文献[11]中给出了三相电枢绕组的合成磁势fa(θ,t)(计及外定子齿槽影响)：

(8)

图8所示为电枢反应磁场磁路，虚线表示不经过阻尼导绕组的磁力线路径，实线为对阻尼绕组产生作用的电枢反应磁场路径，其中前者为主导。

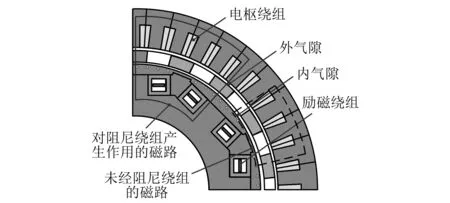
图8 电枢磁场磁路图

电枢反应磁场经调磁环转子以及内外定子齿共同调制产生的内气隙磁密Bina(θ,t)如下：

Bina(θ,t)=f2(θ,t)·λr(θ,t)·λin(θ)=

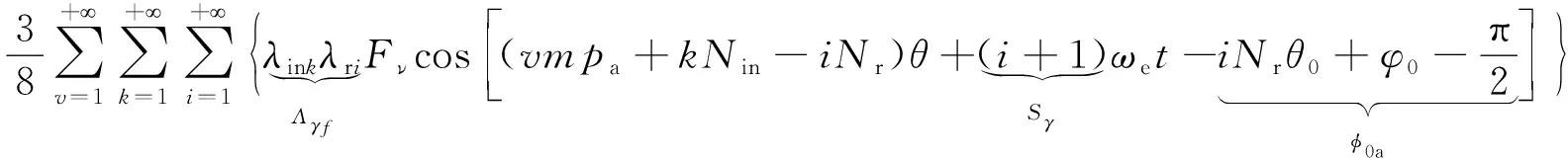
(9)

3 阻尼绕组中的感应磁场解析

为了方便后续分析，需对电枢反应磁场和励磁磁场分别单独作用下产生的内气隙磁密进行简化。将气隙磁通密度统一表达为

Bin(θ,t)=Fγ(θ,t)Λγ(θ,t)

(10)

则式(7)和式(9)可进一步简化表达为

(11)

式中:Λγ为内气隙总磁导，Fγ为谐波磁势幅值，根据磁动势调制来源分为Fγa和Fγf；γa和γf为内气隙谐波磁场极对数；sγ为内气隙谐波磁场相对电枢磁场旋转速度的倍数；φ0为γ次谐波磁场；Λγa为电枢磁场单独作用时的内气隙磁导，等于内定子磁导与转子磁导的乘积，如γa取|νmpa|时，对应Λγa为 (λr0·λin0)，同理，定义Λγf为励磁磁场单独作用时的内气隙磁导，即λri。

设DS-HTSM内定子一个极距内共有2nc根阻尼导条，当内气隙磁场与阻尼条有相对运动时，则会在端部闭合的阻尼条中产生感应电流，继而电磁感应生成交流磁场，作用于原交变磁场。

3.1 阻尼导条中的感应电流

由于不同阻尼回路所占空间面积对应的相位差不同[12-13]，将其分为极弧回路(沿d轴对称)和极间回路(沿q轴对称)。其中，内定子的外径用Rin表示，内定子的极对数用pin表示。以励磁磁场作用于阻尼绕组为例，从极弧与极间回路分别说明不同类型阻尼回路中感应电流原理。

3.1.1 励磁磁场γ次谐波磁势在极弧(沿d轴对称)回路的感应电流

首先，选择同一定子齿对应的一个极距内相邻2根阻尼导条作为一个阻尼回路，阻尼导条之间的弧长为l1。根据弧长公式计算对应的空间机械角度，为α1=l1/Rin，得到电枢磁场γ次谐波在极弧阻尼回路中的感应电动势为

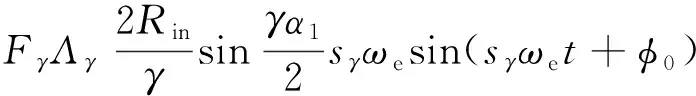
(12)

忽略端部阻抗及槽漏抗，则极弧下对应的阻尼回路等效电路如图9所示。

图9 极弧阻尼回路等效电路

其中，每根阻尼导条的电抗相同:

x1=x2=x3=…=x

(13)

对应极弧下的阻尼回路中的电流幅值相同:

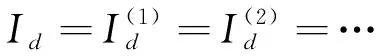
(14)

根据图9中等效电路的虚线标记回路，列写的电动势平衡方程式为

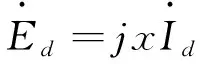
(15)

式中：x为极弧阻尼回路的气隙电抗,x=sγωeλγ1;λγ1为励磁磁场经过单位轴向阻尼导条的气隙磁导,λγ1=μ0l1/δe;δe为等效内气隙长度。

结合式(12)～式(15)可得单个极弧回路中阻尼导条中的电流为

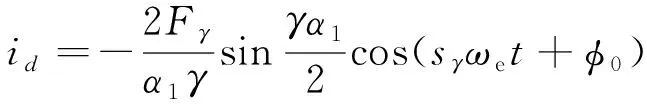
(16)

3.1.2 励磁磁场γ次谐波在极间(沿q轴对称)回路的感应电流

选择不同定子齿对应的一个极距内相邻2根阻尼导条作为一个阻尼回路，极间两根阻尼导条之间的弧长为l2，按照弧长公式，对应的空间机械角度为α2=l2/Rin，确定励磁磁场γ次谐波在极间阻尼回路中的感应电动势为

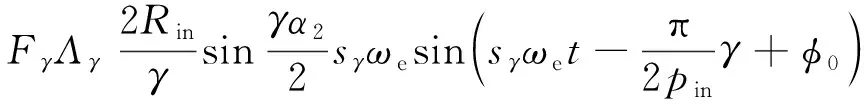
(17)

同理，不计端部阻抗和漏抗，则极间阻尼回路等效电路如图10所示。

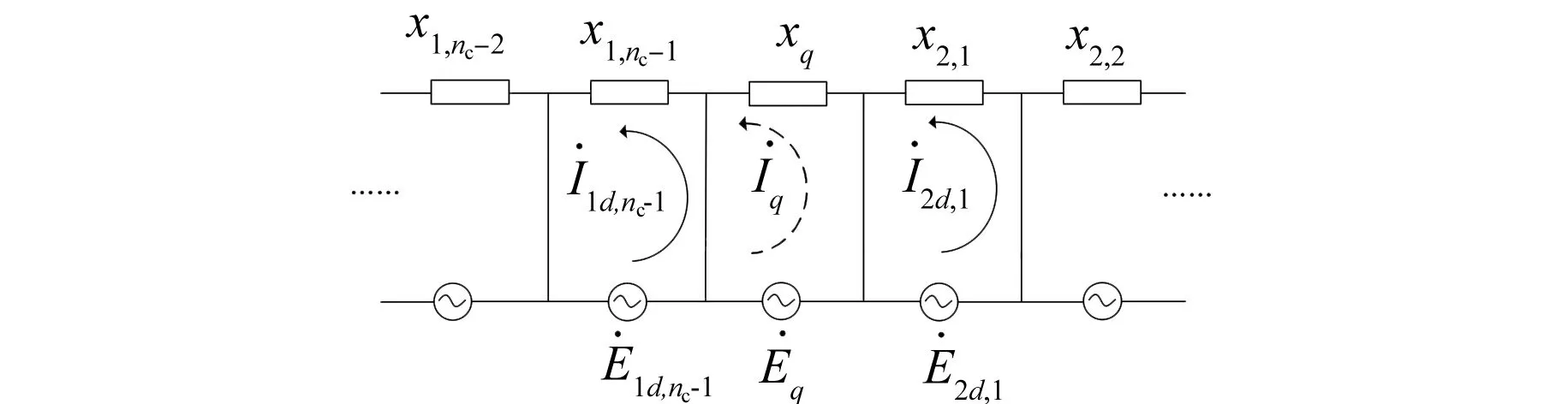
图10 极间阻尼回路等效电路

对比极弧阻尼回路电流方程，根据图10中等效电路的虚线标记回路，极间回路的电动势平衡方程列写为

(18)

式中：xq为阻尼导条回路的气隙电抗,xq=sγωeλγ2；λγ2为励磁磁场经过单位轴向阻尼导条的磁导,λγ2=μ0l2/δe;δe为等效内气隙长度。

同理，结合式(17)和式(18)可得单个极间回路中阻尼导条中的电流为

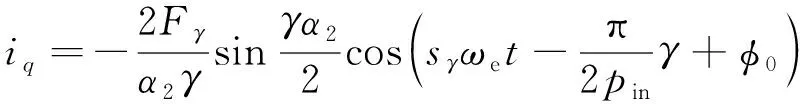
(19)

3.2 阻尼绕组中的感应磁动势

根据电磁感应定律，阻尼回路中的电流生成磁场，反过来作用到励磁磁场。DS-HTSM中的2nc×2pin根阻尼导条采用鼠笼导条式结构设计加工，为了方便计算，在推导极弧阻尼回路(沿d轴对称)和极间阻尼回路(沿q轴对称)的磁动势[14]时，选择图11所示的连接条部分。

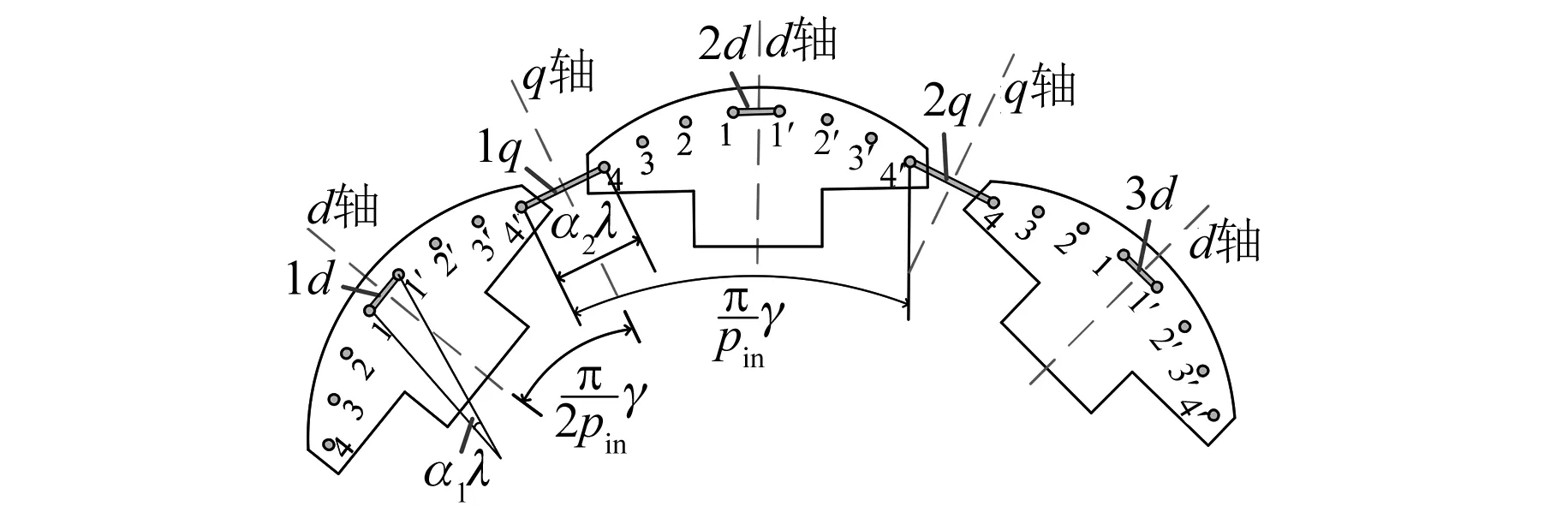
图11 阻尼回路连接图

3.2.1 极弧下阻尼回路产生的磁动势

阻尼回路连接如图11所示，取一个极面上靠近中线相邻2根阻尼导条构成1-1′回路，同时取阻尼回路的中线为坐标轴。由于电机内定子每个磁极下对应1-1′回路，共2pin个1-1′回路。

图12 极弧下单个阻尼回路感应磁势波形

图12所示为一个磁极对应的1-1′回路磁动势波形，进行傅氏分解可得

cos(sγωet+φ0)cos(μθ)=

cos(sγωet±μθ+φ0)

(20)

由图11可知，沿顺时针方向，相邻磁极阻尼回路的电流滞后第1个磁极的 1-1′阻尼回路电流πγ/pin，在空间上相差π/pin，因此第2个磁极的1-1′阻尼回路电流的感应磁动势为

(21)

同理，第n个磁极下的1-1′阻尼回路电流的感应磁动势为

(22)

则电机中2pin个1-1′阻尼回路的总磁动势为

(23)

可见，阻尼回路电流在感应γ次谐波磁动势之外，还会在内定子上产生其他的齿谐波感应磁动势。此时，取μ=γ+2Kpin(其中,K=0,±1,±2,…,正负号代表齿谐波感应磁动势相对γ次谐波旋转方向)，则2Kpin次谐波磁动势即为内定子开槽引起的齿谐波附加磁动势。进一步简化可以得到

cos[sγωet-μθ+φ0]

(24)

由图11还可知，由于1′-2′回路电流滞后1-1′回路α1γ，在空间上相差α1，则2pin个磁极下1′-2′阻尼回路的总磁动势为

cos[sγωet-μ(θ-α1)-α1γ+φ0]=

cos[sγωet-μθ-α1(γ-μ)+φ0]

(25)

由于阻尼回路以极面中心对称，极弧下的阻尼回路幅值相等，按照绕组的分布规律，总磁动势可以表达为

cos[sγωet-μθ-(m-1)α1(γ-μ)+φ0]=

(26)

3.2.2 极间阻尼回路产生的磁动势

图11中，1q回路代表一个极间阻尼回路。由于1q回路电流落后极弧下1-1′回路πγ/2pin，在空间上相差π/2pin，1q阻尼回路的磁动势为

(27)

同理，对于其他极间阻尼回路感应的磁动势可表示为

(28)

其中，n=1,2,3,…,Nd。

极间阻尼回路的总磁动势为

(29)

3.2.3 所有阻尼回路产生的总磁动势

阻尼回路的磁动势满足向量基本定理，则将极弧阻尼回路总磁动势和极间阻尼回路总磁动势，即式(26)和式(29)相加，可以得到所有阻尼回路的总磁动势F可表示为

F=Fd+Fq=

cos[Sγωet-(γ+2Kpin)θ+φ0]=

cos[Sγωet-(γ+2Kpin)θ+φ0]

(30)

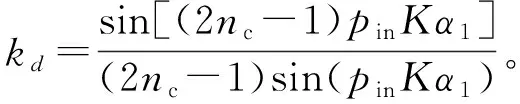
3.3 阻尼绕组感应磁动势对气隙磁场的影响

在考虑阻尼绕组产生的磁动势对气隙磁场的影响时，需保证在对电枢反应磁场发挥有效作用的同时，基本对励磁磁场无影响。以图2所示的DS-HTSM为例，结合表1中电机的部分参数，分析阻尼绕组对谐波磁场的影响。

表1 DS-HTSM部分参数

3.3.1 阻尼绕组磁动势作用于电枢磁场

由式(30)分析可知，电枢反应磁场经由调磁环转子和内定子齿共同调制产生的γa次齿谐波磁场切割阻尼绕组会感应出γa+2Kpin次谐波磁场，其中，2Kpin次谐波为附加齿谐波磁场。随着谐波次数的增加，磁场谐波幅值减少，故仅分析K值取10以内。

当K=0，kd=7时，式(30)的幅值为负，故阻尼导条中感应出与主磁场反向的磁动势，从而起到削弱γ次谐波磁场的作用，此时对于所有的高次谐波皆可以应用。从图13可看出，当K取非零整数时，绕组分布系数kd的值呈周期性分布，且幅值在±0.71之间，同时，由于其在一个周期内有正有负，从而导致阻尼导条中感应出高次谐波磁动势的方向无法确定。故只研究一个周期内的随着K值变化，阻尼导条对高次电枢谐波磁场的影响。

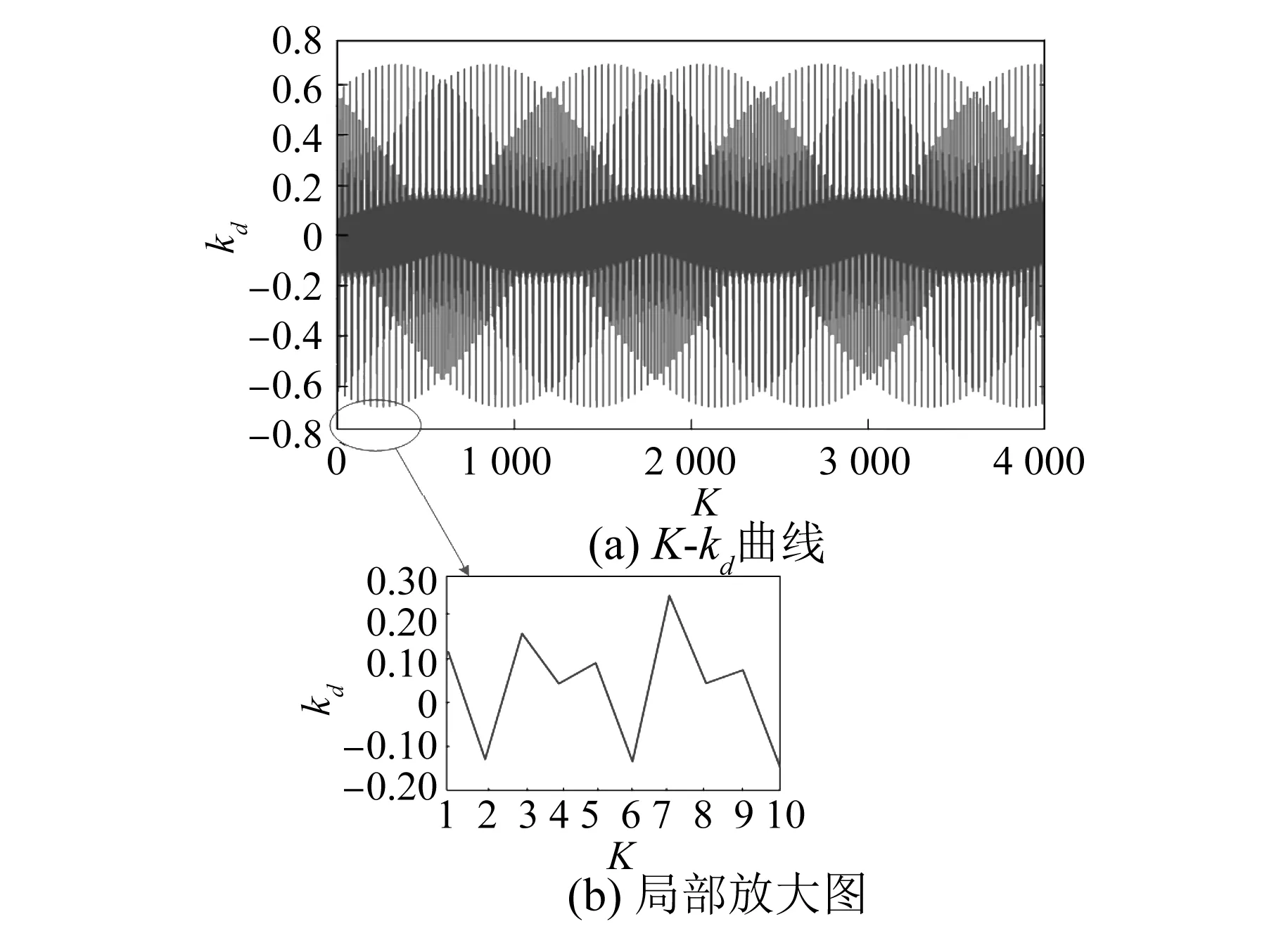
图13 K-kd曲线图

当K=±1，kd取正值时，式(30)中第1项取正值，第2项取负值，但是第1项的幅值远大于第2项，且幅值和为负，因此阻尼导条中感应出的附加齿谐波磁动势与主磁场反向，可以削弱有效电枢谐波磁场的磁动势，即|vmpa+kNin|、|vmpa+kNin-iNr|。当K取偶数时，由于对应的kd正负值不一致，要分别分析：当K=±2, ±6, ±10，kd取负值时，式(30)中第1项取负值，第2项取正值，但是第1项小于第2项的幅值，幅值和为较小的正值，因此会小幅度地增强γa±4pin、γa±12pin、γa±20pin次电枢谐波磁场；当K= ±4,±8，kd取较小的正值时，第1、2项均取正，幅值和也为较小的负值， 因此对于γa±8pin、γa±16pin、γa±20pin次电枢谐波磁场而言，也是小幅度增强。同理可以分析K取奇数时，当K=±3，±5，±7，±9，kd取正值时，式(30)中幅值和的第1项取正值，第2项取负值，但是第一项的幅值大于第2项，幅值和取负值，因此可以削弱γa±6pin、γa±10pin、γa±14pin、γa±18pin次电枢谐波磁场，但是变化程度很小。总的来说，当K取大于±1的值时，阻尼导条对有效谐波之外地偶数次齿谐波磁场影响很小，而对|vmpa+kNin|、|vmpa+kNin-iNr|的有效谐波磁场可以进行抑制。

3.3.2 阻尼绕组磁动势作用于励磁磁场

同样地，结合式(30)可以得到，励磁磁场经调磁环转子调制产的γf次交流谐波切割阻尼绕组会感应出γf+2Kpin次附加齿谐波磁场。下面研究一个周期内的K值变化时，阻尼导条对励磁交流谐波磁场的影响。

当K=0时，kd=7，式(30)的幅值和为负，阻尼导条中感应出与主磁场反向的磁动势，从而起到削弱γf次即|jNin±iNr|次谐波磁场的作用；而当K不为0时，阻尼导条中感应2Kpin次附加齿谐波磁势，仅对偶次谐波有微弱影响，而对直流励磁磁场无影响。

然而由于超导励磁磁场远强于阻尼绕组磁场，对超导励磁场的影响可以忽略，后续的有限元分析也证明了这一点。综上所述，DS-HTSM在放置阻尼绕组后，对励磁直流磁场基本无影响，而对于交流电枢磁场的有效谐波起到削弱作用，即针对基波磁场发挥作用。

4 有限元验证

借助有限元分析软件进行分析时，忽略电机的端部效应，采用二维电磁场模型进行分析。且由于电机是整数槽绕组，满足对称性，为简化模型运行，故采用二分之一模型进行分析。同时，在对比分析添加阻尼导条结构对励磁特性的影响时，要保证模型设置的条件、参数以及网格剖分大小始终不变，仅改变阻尼导条的材料以及电路参数，通过对比是否添加阻尼导条时，DS-HTSM超导励磁线圈的磁密变化，来验证前述理论的正确性。

鉴于超导电机结构对称，内定子四对极下对应圆周位置性能一致，因此只需分析一个SC线圈上的磁场。因铁磁材料的磁阻远小于杜瓦中空气磁阻，大部分的径向电枢磁力线沿内定子轭部(图中实线部分)穿过，而少量的电枢磁力线沿内定子极靴圆周经阻尼导条穿过。因此，根据电枢反应磁力线的闭合路径，结合阻尼导条的作用机理，仅研究沿切向的电枢磁力线对SC励磁绕组的影响即可。在SC线圈表面沿切向均匀取6个磁密指示点(包含边角位置)，分析SC线圈周围的谐波磁场，如图14所示。设置电路参数时，按照超导电机设计时取槽满率为0.7，在电枢绕组上通入28.28 A的三相对称电流，励磁绕组通入40 A的直流电流。6个磁密指示点的切向磁密的频谱分析结果如图15所示。

图14 SC线圈的具体取点位置

SC线圈工作在超导状态的条件之一是处于临界磁场中，而电枢反应高次谐波磁力线进入内定子后，交变的磁场会直接影响SC线圈周围恒定的临界磁场，甚至会通过电磁感应在SC线圈上感应出附加电流，影响另一个条件—临界电流。因此，必须要减少电枢反应高次谐波磁力线进入到励磁磁场中。

由图15的SC线圈磁密对比可以看到，在加入阻尼导条后，励磁绕组对应位置的基波磁密分别被削弱了0.19、0.78、0.29、0.57、0.16、0.10 mT，即分别下降了23%、65%、45%、52.1%、48.48%、35.7%。但是对于其他极对数的谐波，无论是奇次还是偶次，相比于基波磁密的变化量而言，其值很小。图15中的5次谐波，尽管基本上处于增强的状态，但是从整体来看，其平均增加幅度以及幅值很小，可忽略不计。因此，阻尼导条中感应出的谐波磁场主要是用于减少90 Hz的基波电枢磁场对励磁磁场的影响。同时，从图16所示的空载内气隙磁密曲线中可以看出，未加阻尼导条与加阻尼导条后的内气隙磁密曲线是基本一致的，说明DS-HTSM在放置阻尼导条后，对励磁磁场基本上无影响。

图15 SC线圈上6个磁密指示点的谐波频谱

图16 空载时内气隙磁密曲线图

对比理论式推导和有限元仿真结果可以发现，DS-HTSM的电枢反应磁场经调磁环转子和内定子调制产生的γa次交变谐波磁场作用于SC线圈，在极靴上放置鼠笼式阻尼导条结构后，利用阻尼回路的电磁感应效应，可以有针对性地降低幅值较高的基波电枢磁场对励磁线圈的影响，而由阻尼导条感应的附加齿谐波磁动势，对电枢绕组的高次谐波磁动势则影响较小，同时对励磁磁场也基本上无影响。这充分说明，阻尼导条结构在保证原励磁磁场强度基本不变的前提下，可减弱基波电枢反应磁场对SC线圈的影响。

5 结 语

本文使用解析法详细地分析了DS-HTSM中所应用的鼠笼式阻尼绕组对SC线圈周围谐波磁场的影响，然后借助有限元法进行了对比验证。电枢反应磁场经由内定子齿和调磁环转子调制产生的内气隙磁密，进入内定子后在阻尼导条中感应出电流，继而由于电磁感应生成一系列的附加齿谐波，反作用于原磁场，尤其是针对基波交流电枢反应磁场，起到很强的削弱作用，对励磁磁场的影响不大。