基于LSDYNA的半圆柱壳爆炸荷载下的能量反应

孙 凯，杨新峰，刘 平

(江苏科技大学 土木工程与建筑学院，镇江 212100)

半圆柱壳结构在许多建筑中得到了广泛的应用，特别是在体育馆、现代图书馆和所有大跨度屋顶的建筑中[1-3].由于高精度及大杀伤性武器的不断出现，军事及民用结构越来越容易受到爆炸荷载的冲击，但在目前大跨度屋面的设计中，很少考虑爆破荷载[4-5].

各向同性壳体结构在爆炸荷载作用下的反应大多与其动力响应有关[6-7].文献[8]采用显式程序LS-DYNA模拟大跨度网壳结构在荷载作用下的动力响应.文献[9]通过数值模拟研究了金属泡沫夹层板爆炸冲击载荷的响应分析.文献[10-11]研究了圆柱壳结构在长时间爆炸压力作用下的试验研究.文献[12]对壳体结构抵抗爆炸荷载反应进行算法协同优化.文献[13]基于外爆荷载建立概率模型，对球面网壳在此模型下失效的机理进行细致研究.文献[14]采用数值方法分析了不同爆炸参数对结构动响应的影响关系.文献[15]对双曲线型壳体结构表面爆炸荷载冲击相互作用进行分析预测.目前大量试验研究都是与爆炸荷载作用下的壳体结构有关的，但是很少将半圆柱壳体在爆炸荷载作用下动力响应的理论和实验结果作比较.文中基于常规爆炸荷载作用下半圆柱壳体的理论研究，并通过数值模拟对能量下降理论进行对比与预测.利用Donnell的阻尼力理论，建立了半圆柱壳爆炸荷载的数学模型，研究了其在爆炸荷载作用下的总能量响应.

1 控制方程

对半径为R，长度为L的典型半圆柱壳(图1)进行了研究，半圆柱壳的两端以简支形式表示，外延点位于坐标原点(0,0,0).基于Love的薄壳假设，Donnell推导出无阻尼载荷的运动方程为：

图1 几何模型Fig.1 Geometry of model

(1)

1.1 能量与壳体厚度的关系

式(1)可以简化为一个8阶线性微分方程，将第2项代入第1项，得到关于∇4p的关系式:

Et+D∇8ω+pst∇4ω″=∇4p

(2)

由于爆炸持续时间较短，壳体的变形速率很小，式(2)左边系数项与t的厚度成线性关系.因此，在同等的爆炸压力、几何形状和材料条件下，位移ω与厚度t近似成反比.当能量与位移ω成正比时，可以推断能量与厚度t成反比.可用Ε=p/t表示，其中，p是常数，由几何形状、材料和爆炸压力确定的.

1.2 压力载荷

基于CONWEP方法模拟导入爆炸压力，将反射压力(正常入射)值和入射压力(侧入射)值相结合.采用LS-DYNA软件，使用关键字*LOAD_BLAST_SECTSET施加荷载，其压力荷载采用式(3)计算结果.图2为数值模拟的爆炸荷载曲线，与式(3)所计算出的数据图形大致相似.

图2 数值模拟中爆炸压力与时间的关系曲线Fig.2 Plot of pressure vs time in theory and numerical simulation

(3)

1.3 能量与位置的关系

压力脉冲的计算公式如下：

(4)

式中：q为TNT当量；外延位置Z指据爆炸中心的距离.假定能量与脉冲成比例，并且作用于爆炸载荷的区域，外延位置的坐标假设为(0，0，Z)，如图3，因为Z是变量，则能量可由此推导为：

图3 外延位置示意图Fig.3 Diagramof denotation position

(5)

式中：p1是一个常数参数，与壳体的材料和几何形状有关.当z=0.5时，E为最大值，即外壳长度的中间值.

2 数值模拟

2.1 模型参数设置

基于有限元软件LS-DYNA对半圆柱钢壳进行爆炸数值模拟，验证理论结果的精确性.模型采用的是半径分别为2.5，5和7.5 m，长度L分别为30和45 m，厚度为0.01 m的半圆柱钢壳，材料为Q235钢，弹性模量2.1×1011Pa，泊松比为0.23.

网格划分后，模型中有7 773个节点和1 080个壳单元.爆炸点设置为(0,0,0)，TNT装药重量为10 kg.爆炸的持续时间设定为0.01 s.

2.2 整体能量反应结果

图4为整体动能、内能与总能量的时程分析.从图4时程曲线中可知，根据能量守恒定律，在爆炸0.01 s之后的总能量保持不变.

图4 能量与时间的关系Fig.4 Plot of energy vs time of statics

2.3 位移结果

图5，6显示了P1位置为(0,0,5)和P2(0,2.5,10)的速率时程和快速傅立叶变换(fast Fourier tranform,FFT)的对应频率，表示壳的振动是与多个频率的结合，并无主要频率.

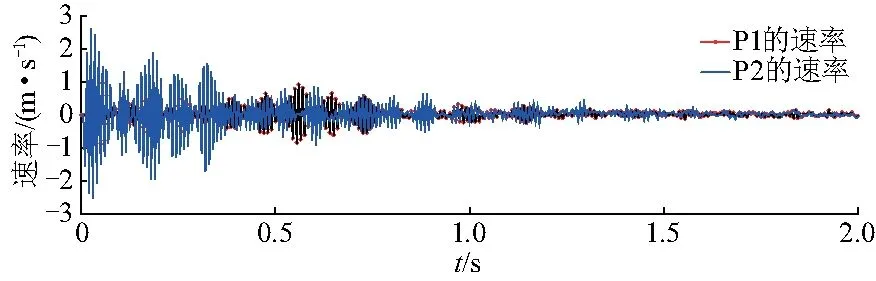
图5 厚度为0.01 m，x=0的速率时程Fig.5 Plot of velocity time history when thickness is 0.01 m,x=0

图6 厚度为0.01 m，x=0的FFT对应频率Fig.6 Plot of FFT corresponding frequency when thickness is 0.01 m,x=0

2.4 爆炸压力分析

爆炸持续时间约为0.1 s，爆炸压力在0.2 s消失，计算数据每0.000 2 s保存一次.图7分别表示0.018，0.036，0.080 s爆炸压力的等高线.其爆炸压力分布基本方向相同.

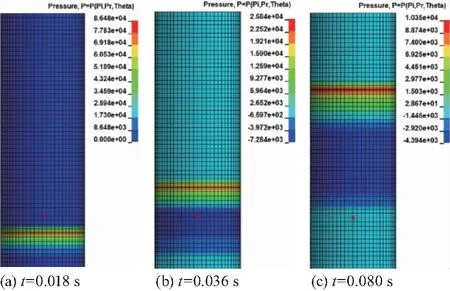
图7 爆炸压力等高线图Fig.7 Contour plot of blast pressure

图8为在不同时间点下(t=0.018,0.036和0.080 s)，爆炸压力与纵向高度的关系图.

图8 在时间点0.018，0.036，0.080 s下爆炸压力与纵向高度的关系Fig.8 Plot of blast pressure vs longitude length with time is 0.018，0.036，0.080 s

3 参数分析

为了得出厚度与能量之间的关系，在R=5.0 m，L=30 m条件下，对厚度分别为0.01，0.015，0.02，0.025，0.03，0.04，0.06，0.10，0.20，0.50 m进行了多次模拟，具体参数如表1.

表1 在坐标原点(0,0,0)上，TNT=10 kg,L=30 m时的初始总能量Table 1 Initial total energy (10·kJ)with TNT=10 kg,L=30 m,denotation at (0,0,0) 10·kJ

3.1 能量与厚度的关系

图9给出了不同点的壳体吸收的能量与厚度的关系，以及理论预测数据.其中，参数P是常数，由数值模拟回归方法确定.由图9可知，计算结果与理论预测结果吻合较好.

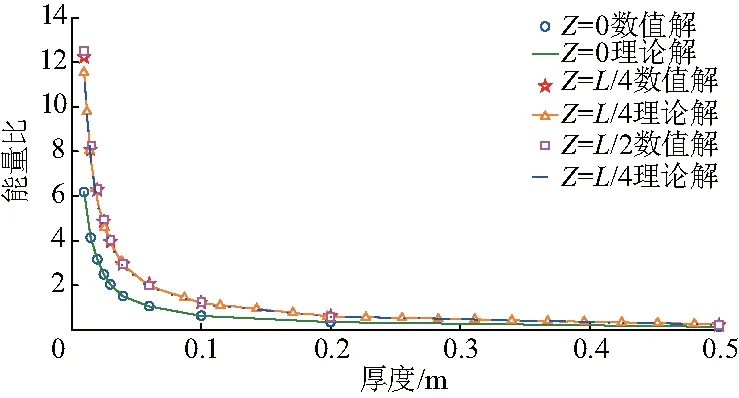
图9 R=5.0 m、L=30 m的能量与厚度关系对比Fig.9 Plot of energy vs thickness with R=5.0 m、L=30 m

3.2 能量与Z/L的关系

此外，为了验证式(5)的正确性，对Z/L不同比例进行数值模拟，模型均采用厚度0.01m，表示位置(0,0,0)，TNT装药量10 kg，具体参数见表2.

表2 当X=0时，TNT=10 kg的初始总能量Table 2 Initial total energy with TNT=10 kg,X=0

在式(5)中，常数参数p1无法预先确定，必须通过回归分析进行计算.采用最小二乘法计算常数参数p1，并将其值列于表3中，并在图10中对数值结果与理论计算结果进行比较.

表3 参数p1的值Table 3 Value of parameter p1

图10 厚度0.01m下，Z/L比值与能量(10·kJ)关系对比Fig.10 Plot of energy(10·kJ)vs ratio with different R and L when thickness 0.01 m

4 结论

文中研究典型钢材料半圆柱壳在爆炸荷载作用下的结构动力响应，采用理论计算和数值模拟方法对半圆柱钢壳在爆炸荷载作用下的动态响应过程以及影响因素进行可一系列的对比分析，得到如下的结论：

(1)当R=5 m、L=30 m及P确定的情况下，能量随着壳体厚度的变化而变化，当厚度增加时，能量呈递减趋势,两者关系成反比.

(2)当壳体厚度确定时，随着壳半径上的表示坐标Z/L增大，能量值变化曲线呈反正切函数递增，两者呈现正比关系.

(3)基于有限元软件LS-DYNA建立的半圆柱壳在爆炸荷载作用下的数值模拟计算模型，与理论推测结果符合较好，验证其正确性.表明计算模型与参数的选取正确，可用于半圆柱钢壳的爆炸能量分析.