基于Workbench的拆解平台单侧起吊过程分析

王庆丰,朱翔宇,祁 斌

(江苏科技大学 船舶与海洋工程学院，镇江212100)

随着海上作业的逐步发展,远海环境下,货物的起重作业逐渐增多,主要集中于大型全回转起重船和起重平台．针对起重作业下,国内外学者对船体、平台等的浮态变化及吊物的运动情况进行了大量研究．文献[1]对小波高、长周期涌浪环境下起重船耦合系统运动响应特性及其机理开展了参数敏感性分析．文献[2-3]通过模型试验的手段对起重船系统运动响应及其机理进行研究．通过数值模拟方法对全回转起重船吊物及船体运动响应情况进行了研究．文献[4]利用Lingo软件对全回转起重船算例进行计算．文献[5]以起重能力1 600 t的起重船为研究对象,采用物理模型试验方法给出了起重船施工作业的波浪条件．文献[6-7]对平台上部模块进行了数值分析．文献[8-10]对半潜平台起重船的性能及浮吊系统进行研究．文献[11-14]对海上起重船响应进行研究．文献[15]对近岛礁浮式平台的运动响应进行了研究．文献[16]对自升式平台码头系泊断裂进行了研究．

文中采用Workbench Aqwa软件对某一非对称拆解平台进行吊重模拟,通过绞机收缩缆绳的方式模拟拆解平台对吊物的起吊过程．通过对数值分析的结果进行研究,得出拆解平台单侧起吊的作业规律以及长时间恒定吊载下平台的稳性变化情况．

1 计算理论

1.1 时域耦合理论

根据Cummins脉冲响应方法,船体在某一时刻的运动可以归为一系列瞬时脉冲运动的叠加,同时将波浪力分解为一系列脉冲响应的组合,由此可以将频域和时域计算联系起来,使得时域计算过程可以应用频率的计算结果．时域分析中运动方程为:

F(1)(t)+F(2)(t)+Fc+Fw+Fb(t)+

Ft(t)+Fe(t)

(1)

式中：M为船体质量矩阵；A为流体附加质量矩阵；C为阻尼矩阵；K为结构总体刚度系数；h(t)为加速度脉冲函数；F(1)(t)为一阶波浪力；F(2)(t)为二阶波浪力；Fc为流阻力；Fw为风阻力；Fb(t)为非线性舭部横摇阻尼力；Ft(t)为系泊缆载荷；F(e)(t)为船体可能受到的如撞击力等其他外力．

(2)

式中，A(ω)、B(ω)分别为频域计算中波浪频率为ω时的附加质量与阻尼系数．

1.2 系泊缆动力分析

对于系泊状态下的船舶,船体与系泊缆之间会相互影响,考虑二者之间的耦合作用能提高计算的可靠性．计入动态分析后,需要考虑系泊缆的质量、阻力、弹性张力和弯矩,可采用将系泊缆沿长度方向离散,将质量,系泊缆内力及外力集中于端点的方法计算系泊缆动态响应．

系泊缆单元的受力方程为:

(3)

式中:m为系泊缆单位长度质量;q为单位长度上分布的力矩载荷矢量;R为系泊缆单元第一个点的位置矢量;Se为系泊缆单元长度;w为系泊缆单元质量;Fh为系泊缆单元单位长度的水动力矢量;T为系泊缆单元第一个点的张力矢量;M为系泊缆单元第一个点的弯矩矢量;V为系泊缆单元第一个点的剪切力矢量．

弯矩和张力与材料的抗弯刚度EI和轴向刚度EA有关:

(4)

式中，ε为系泊缆单元的轴向应变．

2 计算模型

2.1 水动力模型

以一非对称无横撑的半潜式拆解平台为研究对象,该平台于150 m水深的海域内进行起重作业．平台主尺度如表1.

表1 主尺度表Table 1 Principal scale table m

该平台在进行起吊作业时,采用十字锚泊系泊方式．平台使用4×2的悬链式系泊布置,主浮筒船首船艉左舷侧各两条系泊缆,副浮筒船首船艉右舷各两条系泊缆．系泊缆布置方式随吃水深度及环境载荷的变化而发生变化．坐标系以平台尾部至艏部方向为x轴正方向,平台中心为原点．以主浮筒外侧为y轴正方向,主浮筒中心为原点,水线面以上为z轴正方向．水动力模型如图1,系泊布置如图2．

图1 水动力模型Fig.1 Hydrodynamic model

图2 系泊布置Fig.2 Mooring layout

文中依据平台资料,建立水动力模型,通过Aqwa的Hydrodynamic Diffraction模块计算分析得到海洋平台的水动力系数．

由图3、4可以看出横摇和纵摇的最大值均发生在10～15 s的周期内,分别出现在浪向角α为90°、180°的情况下,在设定环境载荷参数时,应避免设置此类波浪周期．

图3 拆解平台横摇传递函数Fig.3 Roll transfer function of platform

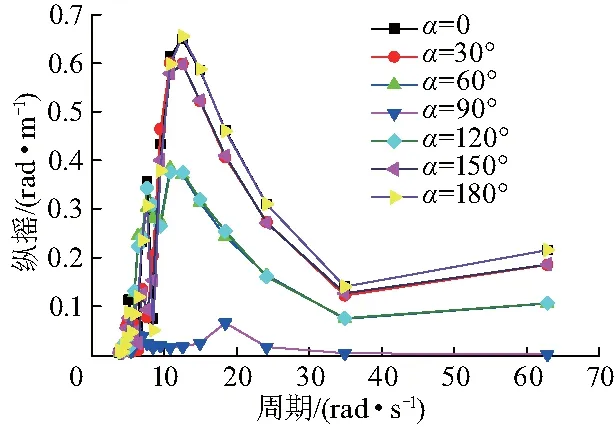
图4 拆解平台纵摇传递函数Fig.4 Pitch transfer function of platform

2.2 环境载荷设置

环境载荷1条件如表2，不规则波谱为JONSWAP谱，如图5．

表2 计算环境载荷1Table 2 Environmental condition

图5 不规则波波谱Fig.5 Irregular wave spectrum

不规则波的方向设置为0,风速为15 m/s,流速为1 m/s,环境载荷入射角都设置为0．

3 计算结果及分析

3.1 不同吊臂旋转角下平台与吊物的运动响应

拆解平台选用主浮筒一侧进行起吊过程模拟,吊臂旋转角β为15°～165°．吊物起吊采用四点起吊布置,通过cable winch操作使得四条起吊缆绳受力一致．吊物自重约为3 000 kg,长为5 m,宽为2 m,每条起吊缆绳受力为8 000 N,环境载荷选用计算环境载荷1,吊物自水下1 m起吊至12 m高处,平台起吊模拟如图6,吊物自身运动响应最值及平台运动响应最值如表3.

图6 平台起吊示意Fig.6 Schematic diagram of platform lifting

表3 起吊过程中平台吊物的运动响应Table 3 Motion response of platform crane during lifting

平台总体运动响应变化较小,由表3可知,除15°吊臂旋转角以外,平台纵荡数值均在0.1以下,而平台纵荡的数值分布与吊物纵荡数值分布趋势相同,当吊臂旋转角β为15°时,吊物纵荡达到最大值．平台垂荡在-0.4 m左右浮动,其中75°～135°下平台垂荡基本保持不变．平台横荡均小于0.27 m,当吊臂旋转角由15°～75°增加时,平台横荡增加,由75°～165°减小时,平台横荡减小．75°时的吊物运动响应曲线如图7～10.

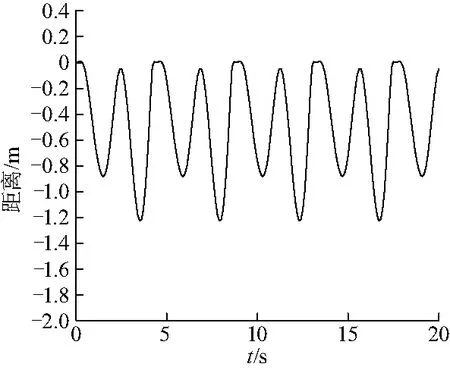
图7 75°时吊物纵荡运动曲线Fig.7 Surge motion curve of crane at 75°

图8 75°时吊物纵向加速度运动曲线Fig.8 Vertical acceleration curve of crane at 75°

图9 75°时吊物横荡运动曲线Fig.9 Swing motion curve of crane at 75°

图10 75°时吊物横向加速度运动曲线Fig.10 Transverse acceleration curve of crane at 75°

取表3中吊物横荡与纵荡运动幅值的绝对值作柱状图(图11、12),分析吊臂旋转角β对吊物运动幅度的影响.

图11 吊物纵荡运动幅度对比Fig.11 Comparing diagram of surge motion amplitude of lifting object

由图11可知,吊物纵荡运动幅值的绝对值随吊臂旋转角整体上呈现先减少后增加的趋势,该趋势与平台的纵荡趋势基本一致．图12中最低点为吊臂旋转角为75°时,此时纵向加速度呈无序状态,说明吊臂旋转角对于吊物纵向运动影响较小．

图12 吊物横荡运动幅度对比Fig.12 Comparing diagram of sway motion amplitude of lifting object

由图12可知,吊物横荡运动幅值绝对值随吊臂旋转角的增加而呈现先增加后减少的趋势,该运动趋势与平台的横荡运动趋势基本一致．因此起吊过程中,吊臂旋转角增加到75°时对平台纵荡有一定抑制作用,对平台横荡则有一定的加强作用．

3.2 不同悬臂角下吊物恒处于一定高度时,平台运动响应

由于Workbench软件不支持吊物恒定于一定高度的数值模拟,因此以固定载荷作为替代,不再考虑吊物的运动响应,重点考虑平台运动响应．

此时将3 000 kg的吊物替换为30 000 N的外加载荷．拆解平台仍采用同样的系泊布置,起重机位于主浮筒一侧,以平台船艏为0,沿逆时针方向,每隔15°为一个工况将360°的作业工况划分为24个作业工况以进行计算．采用上文的环境载荷工况1进行计算．计算载荷1为一般作业工况,碍于篇幅所限从中选出0、60°、90°、120°、180°、-60°、-90°、-120°这8个变化较为明显的情形进行分析．

环境载荷1下吊臂角下平台运动响应时历与系泊缆时历曲线如图13、14,汇总结果如表4．

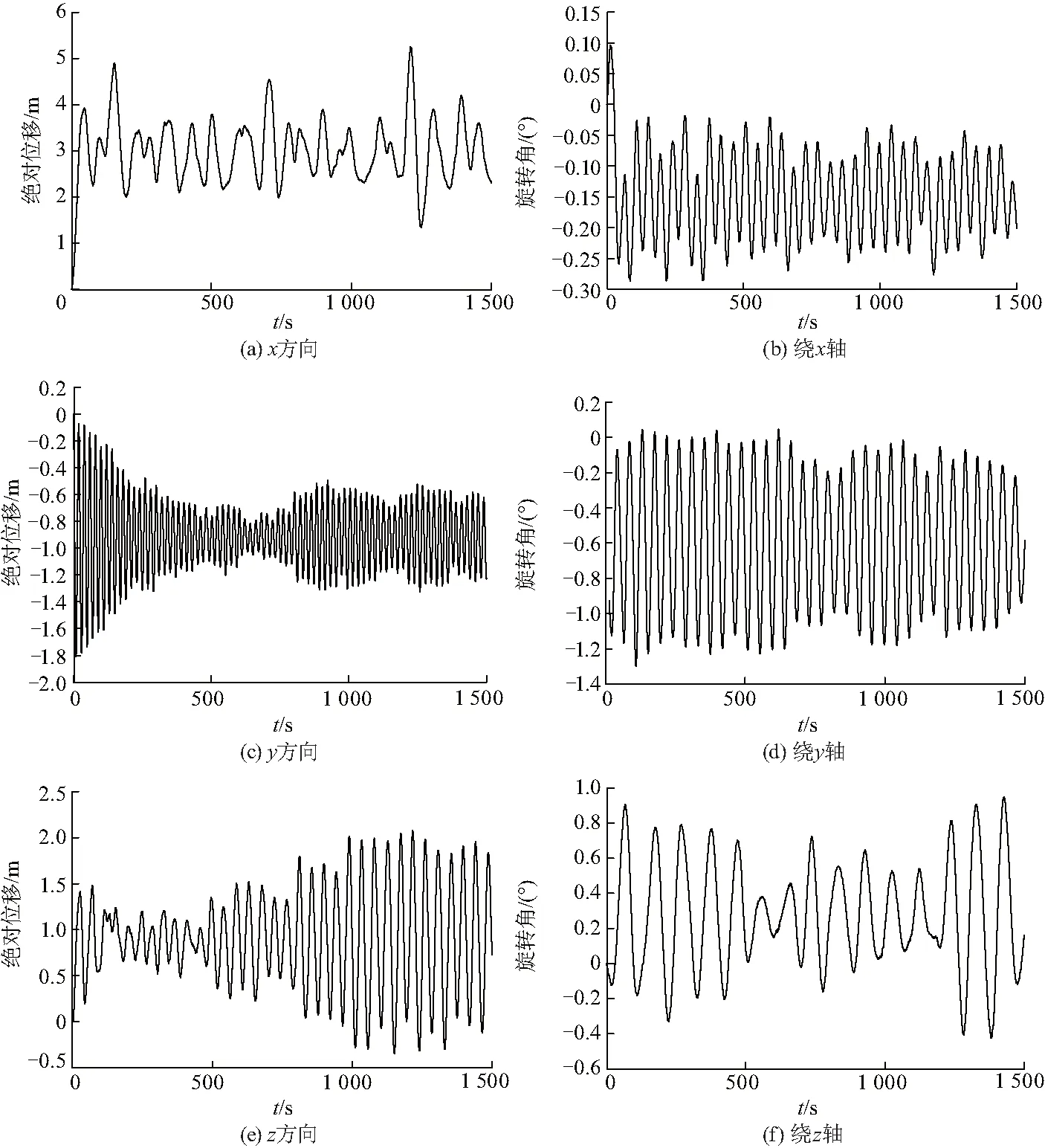
图13 平台六自由度运动响应曲线Fig.13 6-DOF motion response curve of platform

从表4中可以看出平台的横摇变化比较明显,吊臂的旋转角β从0变化至90°期间,船体的横摇角逐渐变大,之后随着吊臂旋转角度继续增大,平台横摇角逐渐减小．纵摇在180°时达到最小,且正负方向运动响应幅值不同．平台纵荡由0趋近180°时减小,并在180°时达到最小．横荡位移受吊臂方向影响在90°时达到最大,而升沉运动全程不受吊臂旋转角的影响,纵荡横荡升沉运动正负方向运动幅值完全一致．

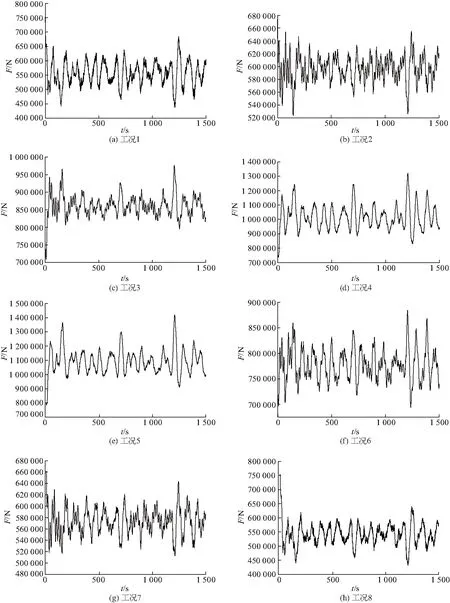
图14 平台系泊缆拉力F曲线Fig.14 Pull curve of platform mooring line

表4 吊重在环境载荷1入射角0计算结果最大值汇总Table 4 Maximum value summary of calculation results when condition1 ais 0

系泊缆的张紧力则随着吊臂旋转角的逐渐改变发生改变,其中4、5号锚缆所受张紧力最大,由于风流载荷入射角为0,与4、5号锚缆呈对向,因此受力最大,也是断裂最可能发生的地方．当由0转向180°的过程中4、5号锚缆张紧力随角度增加而下降,并于180°达到锚缆张紧力的最小值,对应纵荡的最小值．1、8号锚链受风流载荷为顺向,因此在吊臂方向改变时无变化,说明3 000 kg载重情况下,风流载荷的对向锚缆受吊臂伸出角度影响最大．

3.3 大吊载下平台运动响应分析

平台运动响应所添加的吊载为30 000 N,而实际作业中平台的吊载可以达到1 500 000 N左右,以1 500 000 N的吊载作为附加载荷,环境载荷及系泊布置的设置同上,将变化趋势较为明显的0、60°、90°、120°、180°、-60°、-90°、-120° 8个工况的计算结果进行汇总,如表5.

表5 吊重在环境载荷1入射角0计算结果最大值汇总Table 5 Maximum value summary of calculation results when cindition1 ais 0

由表5可以发现,垂荡位移较之于表4,吃水深度发生了明显增加,由60°至-180°、-60°至-120°的β变化中,吃水深度逐渐减小,吃水最小值发生在-120°．在表4所对应工况下,β值改变,横荡及横摇数值改变较小,而在较重吊载情况下,吊载方向及β值对平台运动自由度数值影响巨大．以β值为0和90°时为例,其对应的横荡横摇数值分别为0.185 m、-0.68°以及6.45 m、-2.42°,数值变化幅度在4倍以上．由表5中纵荡数值的变化可以看出,当吊载增加时,β越接近90°,纵荡抑制现象越明显,即图中60°、90°、120°、-60°、-90°、-120°所示．

大吊载下,4、5号系泊缆受力趋势与表4基本一致．与表4中其余系泊缆受力无明显变化不同,表5中除4、5号系泊缆外,其余6根系泊缆受力均出现明显变化,1～4号系泊缆在-60°、-90°、-120°吊臂旋转角时的受力均远超过90°与120°吊臂旋转角时系泊缆的受力,由图2可知,这4根系泊缆均布置在拆解平台的副浮筒方向,由于吊机位于主浮筒一侧,此时力矩较长,系泊缆受力较大．同样,当吊臂旋转角位于主浮筒一侧时,5～8号系泊缆在-60°、-90°、-120°时受力较大．其中系泊缆受力的最大值发生在β角为0时,30°β下受力也较大,应当避免0、30°下进行长时间恒定吊载．

此时将表5的中纵倾角与横倾角整理为倾角——吊臂旋转角的折线，如图15、16.

图15 横倾角随β变化情况Fig.15 Change of roll angle with β

图16 纵倾角随β的变化情况Fig.16 Change of trim angle with β

横倾角的最大值为2.5°,发生在β为90°时,纵倾角的最大值为2.3°发生在β为0时．除去图15、16中的极值情况,纵倾角的变化幅值小于横倾角．因此,拆解平台单侧吊机起重作业时应当重点注意横倾角的变化．根据CCS的起重平台浮态稳性标准,横倾角应当小于5°,纵倾角应当小于2.5°．因此在1 500 000 N载荷下平台起重稳性保持在安全范围内．

4 结论

(1)进行单侧起吊时,吊物纵荡运动幅值的绝对值随吊臂旋转角增加整体上呈现先减少后增加的趋势,横荡运动幅值绝对值随吊臂旋转角的增加而呈现先增加后减少的趋势,吊物的运动趋势与平台运动趋势保持一致．吊臂旋转角增加到75°时对平台纵荡有一定抑制作用,对平台横荡有一定的加强作用．

(2)在添加30 000 N吊载的情况下,平台的最大受力系泊缆为4、5号系泊缆,均为风流载荷的对向系泊缆．吊臂的旋转角从0变化至90°期间,船体的横摇角逐渐变大,之后随着吊臂旋转角度的增大船体横摇角逐渐减小．纵摇在180°时达到最小,且正负方向运动响应幅值不同．平台纵荡由0趋近180°时减小,并在180°时达到最小．横荡位移受吊臂方向影响在90°时达到最大,而升沉运动全程不受吊臂旋转角的影响,纵荡横荡升沉运动正负方向运动幅值完全一致．

(3)添加了1 500 000 N吊载后,吊臂旋转角角度对船体自由度影响巨大,超过环境载荷入射角对平台运动的影响,仍存在着对纵荡运动的抑制作用．吊臂旋转角为0、30°、90°时,平台的运动响应较大,应当避免此工况下进行起吊作业．

(4)对360°工况下的平台起吊作业进行数值模拟,结果表明拆解平台在较大载荷即1 500 000 N的情况下,仍符合CCS的稳性要求,就实际作业中的平台稳性变化情况,为工程人员提供参考．