论在小学数学课堂教学中实现数与形的共融共通

李胜元

当代心理学家强调要加强学生知识整合能力的培养，让学生懂得运用知识来解决问题。数形结合通过把直观的“形”和理性的“数”结合起来，能帮助学生克服认知困难并形成知识体系，提升数学學科素养。

一、用“形”的形象来理解数的抽象性

在课堂教学中，可以通过合理运用图形的直观性来辅助学生理解小学数学的抽象算理，实现抽象知识的具象化呈现，帮助学生更好地理解数学的本质问题。

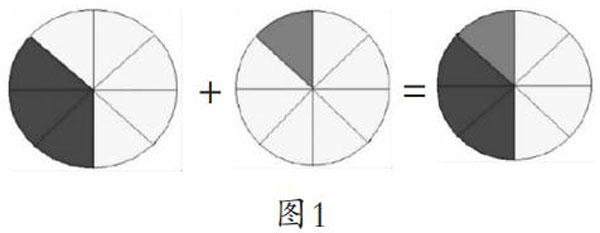
分数单位数量的叠加。

同样在“异分母分数加、减法”的教学时，同样可以借助图形的直观展示，让学生了解到在分数单位不同的情况下，数量直接相加减不符合分数意义中的平均分，需要转化为同分母的分数才能计算，这让学生对异分母分数加减法的算理有了更为直观的认识。

的是使用通分的方式来解决问题，但至于为什么要通分，他们对其中的原理还讲得不透彻。此时，笔者再次借助图形引导学生进行知识迁移，将异分母分数转化成同分母分数的过程展现出来（图2），让学生有了更直观的认识：当对两个分数进行通分后，将分数的分母化成一样，也就是它们的分数单位也一样，这时候就可以直接数出纸张类垃圾和废金属类垃圾一共占了多少格，也就得到了这两个分数的和。

二、用“数”的理性来分析形的特征

在课堂教学中善用数形结合，也可以帮助学生更好更快掌握概念内涵，使复杂的图形问题转化为简单的数量关系来处理，从代数的角度来帮助学生理解图形的本质特征。

例如，在进行“长方形与正方形”的教学时，笔者首先让学生根据图形边的长度特点对一些图形进行分类，紧接着引导学生利用直尺、三角板等工具对长方形和正方形的边长与角的大小进行验证，进而发现长方形和正方形的基本特征（都是四条直边和四个直角）。随后在长方形和正方形的对比教学中，笔者引导学生借助表格（表格略）与字母的形式，对两者的特征进行对比，帮助学生对两种图形的本质特征（正方形的四条边都相等，可以都用a表示;长方形的长和宽不相同，分别用a和b表示，a≠b）有了更进一步的理解。

同样，在进行 “三角形三边关系”的教学时，如果单纯借助教具的操作，学生很难对三边关系有数理上的认识。因此，就需要引导学生借助“数”的特点来对三角形三边关系做进一步的探究。笔者先出示3根小棒（不告知长度），让学生大胆地猜一猜这3根小棒能围成一个三角形，并让学生说说是怎么想的。紧接着，引导学生小组合作，利用学具进行拼摆探究，并将结果填写在探究记录表（见后文附表）上。之后让学生围绕表格中所填的数的特点展开交流，学生很快发现能围成三角形三条边的关系（a+b>c、a>c-b，b+c>a、b>a-c，a+c>b、c>b-a）。至此，学生对于三角形的三条边的长度关系有了一个较为清晰的认识。

三、共融互通解决复杂问题

在复杂问题的探究中，巧借线段图像能将实际问题与文字信息联系起来，能够让学生有理有据地分析，让学生思维的发展有依托。

例如，在进行“乘法分配律”教学时，很多学生对分配律的理解存在一定的困难，很容易与乘法的结合律混在一起，其主要原因是由于学生对分配律的算理的不理解。因此在教学时，教师可以合理借助图形来帮助学生对此定律加以认识。课堂中可以借助求大长方形的面积（图3）这个问题，引导学生用多种方法来解决。通过对图形面积的不同方法展示，学生发现4×8+4×2=（8+2）×4，且都等于大长方形的面积，进而把乘法分配律和求图形的面积结合起来，让抽象的运算定律通过图形的形式来展现，帮助学生更快、更准确把握住乘法分配律的内涵并能准确运用。

又如，探究这样一道复杂问题：小丽的卧室长4.6米，宽3.4米，卧室平面图分成四个小长方形区域（图4左）。小丽用竖式计算出卧室的总面积（图4右）。箭头所指的这一步表示的是哪个区域的面积？

本题对学生的思维层次的要求相对较高，需要学生把竖式的算理和图形面积的计算结合起来思考。竖式计算中箭头所指的“138”表示的是1380个0.01，它是由3×4.6得来的。而3×4.6在题目中是指长4.6米、宽3米，因此，3×4.6表示求一个长4.6米、宽3米的长方形的面积。接下来，再结合左边的图，最终找到长4.6米、宽3米的长方形即图形①+④所组成的部分。在教学中，伴随着问题的解决，慢慢培养了学生把数和形结合起来的意识，在今后的复杂问题解决中也就能加以应用了。

（作者单位：福建省厦门市思明区莲前小学 本专辑责任编辑：王振辉）

信息

《新教师》编辑部：福建省福州市鼓楼区梦山路27号    邮政编码：350025

编后记

小学生的抽象思维能力还比较薄弱，对于数学概念、定律等的理解存在一定的困难，而利用图形的演示能帮助学生深化对概念及定律的理解，促进学生掌握数形结合策略以解决问题。本专辑探讨了数形结合策略在教学中的多种新尝试，希望所刊发的文章对一线教师能有所启发。