碳排放权交易市场与新能源市场的动态相依关系研究：以我国碳市场试点为例

王 许，乔清薇,陈 霄

引 言

目前,我国将碳排放权交易机制作为完成2030年碳排放达峰目标以有效应对气候变化的重要市场化减排政策工具。自2013年起，深圳、上海、北京、广东、天津、湖北、重庆和福建相继启动碳排放权交易市场的试点工作。2017年底，我国正式宣布以发电行业为突破口，分三个阶段开展全国碳排放权交易市场的建设工作。从理论上说，政策制定者通过开展排放权交易可以使“污染排放”成为一种对环境容量资源使用的限量使用权，而排放厂商根据各自对排放权使用的需求进行自由交易,能够通过市场机制实现最优的排污权均衡价格，从而实现有效降低排放的目的(Wang et al，2018；Wang et al，2019；Zhu et al，2020)。

但更需要强调的是，碳排放权交易机制的实施不仅能够有效促进相关国家和地区总量减排目标的实现，也会有力推动新能源公司的发展。此时，政策制定者向履约企业发放碳排放的初始配额。而履约企业需要在能源使用与排放减少间进行权衡，并通过配额交易以在规定的时间内完成减排任务。当传统能源企业和新能源企业均参与到碳排放权交易机制时，前者可能需要在市场上购买配额或者投资新能源技术以完成减排任务，而后者则在出售其研发技术的同时还可以通过出售由此产生的减排量而获得更多的市场收益。因此，从理论上说，政府通过推动碳排放权交易机制，可以为以低碳、绿色为特点的新能源公司提供新的融集资金的渠道，有效促进新能源产业的发展，从而带动全社会的低碳转型。

在市场经济体制下，碳交易市场的推动将通过碳价格信号的引入，影响新能源公司股价的波动，从而影响新能源公司的市场价值与未来发展：一方面，碳配额的市场价格如果能为相关行业提供明确的减排与技术更新投资的信号，会为新能源公司所研发的新技术带来更广阔的市场前景，进而促进新能源公司市场价值的提升；另一方面，新能源公司可以参与到碳排放权交易机制中，并以碳配额的市场交易价格出售排放配额，又能获得一定的市场收益。因此，完善的碳排放权交易机制可以提供更为有效的市场价格信号，有利于新能源产业的发展。而我们通过研究碳排放权交易市场和新能源市场间资产价格的相依关系，可以为推动碳排放权交易机制的优化和新能源政策的完善提供一定的理论支撑。

本文运用市场供求模型，通过分析传统能源市场和新能源市场因市场化减排机制的引入而发生的变化，以揭示碳排放权交易市场与新能源市场资产价格间的相互影响。早期的研究多关注于减排机制与可再生能源政策间存在交叉而影响实施效果的现象(Nelson，2008；Linares et al，2008)，或者研究碳减排机制对可再生能源市场的影响(Bird et al，2008；Mathews，2008；Lewis，2010)，但均缺乏经济学的机理分析。向量自回归(VAR)模型等经典计量方法被用于实证分析碳排放权交易价格对新能源公司股票价值或可再生能源绿色证书的影响(秦天程，2014；Schusser et al，2018)。由此认为：第一，目前的研究仅从减排政策与可再生能源政策上开展研究，较少地关注新能源产业市场价值的变化；第二，相关的计量经济研究更多地关注碳减排政策对新能源市场的单向影响而忽视了二者间的交互作用，缺乏相关的理论分析。所以，在实证分析碳排放权交易市场与新能源市场资产价格的相依结构之前，首先依据市场供求模型提出相关的假设，并由后续的实证分析加以论证。

经典的Copula-GARCH模型可用来验证上述理论假设，从而探讨碳排放权交易市场和新能源市场资产价格的相依结构。Copula理论由于可以将相关变量的边缘分布与其相依结构分开研究而无需对边缘分布函数加以限制(Sklar，1959；Nelson，2007)，因此被广泛用于刻画能源价格间非对称、非线性的相依结构(Wen et al，2012；姬强等，2016；Liu et al，2017；Mensi et al，2017)。而这一方法多用于分析碳排放交易的现货与期货价格间的相依关系(吴恒煜和胡根华，2014)以及碳排放权交易市场与其他市场价格的相互影响(王倩，路京京，2018)，很少用于研究碳排放权交易市场和新能源市场间的相依关系。经典的GARCH类模型已被广泛用于研究碳排放权交易市场价格的时变特征(Benz et al，2009；Chevallier，2011；Chang et al，2017；胡根华等，2017)，因而可被用以表征所构建Copula模型的边缘分布函数。同时，还比较分析了时变Copula函数和动态条件相关DCC-GRACH模型在刻画两市场资产价格动态相依结构的差异。最后需要说明的是，以往学者采用计量经济方法关注碳排放权交易市场时,更多地关注于碳排放权交易价格的形成机制(Aatola et al，2013；Koch et al，2014；Tan et al，2017)或碳市场与其他商品市场间的相互影响(Balclar et al，2016；Moreno et al，2017；Zeng et al，2017；Wang et al，2018)，没有更多地关注碳排放权交易市场与新能源产业发展间的相互影响，更没有深入研究两者资产价格间的相依结构。

同时，本文以我国碳排放权交易市场和新能源行业板块的相关数据开展实证分析。作为全球最大的温室气体排放国，我国已在8省区市碳排放权交易试点的基础上，于2017年底正式启动了全国碳排放权交易体系。由于该市场有望成为全球最大的碳排放权交易市场，选择其作为实证分析的对象是十分合适的。具体而言，将分别选取较为代表性的深圳碳排放权交易市场的配额价格与国证新能源指数作为样本对象，并运用Copula-GARCH模型来研究我国碳排放权交易市场与新能源市场间的相依关系。

综上所述，立足当前我国在运用市场化减排机制控制温室气体排放，同时大力支持新能源产业发展的现实背景，对碳排放权交易市场和新能源市场资产价格的相依结构加以研究，其边际贡献主要体现在：第一，提出有关碳市场与新能源市场间资产价格相依关系的理论假设，运用市场供求模型分析市场化减排机制的引入对产品市场均衡的影响；第二，将经典的Copula理论与GARCH模型运用到对碳市场和新能源市场资产价格波动及其相依结构的分析中；第三，以我国碳排放权交易试点地区的配额市场价格和新能源产业板块指数为样本，开展相关的实证分析，其结论将为我国在减排机制设计与新能源产业政策的协调上提出一定的政策建议。

一、 碳排放权交易市场与新能源市场资产价格相依性的理论假设

本文通过运用简单供需关系模型，分析碳排放权交易市场的引入促使传统能源企业向新能源公司转型的行为，并就碳排放权交易市场与新能源市场资产价格的相关性提出理论假设。图1和图2分别表示了当传统能源企业和新能源企业被纳入碳排放权交易机制时，生产产品市场均衡结果的变化。

传统能源企业在碳排放权交易机制中的行为如图1所示。该企业产品(如煤电企业所生产的电力)在参与碳排放权交易前的供给曲线S1与需求曲线D1的交点M反映了期初的市场均衡情况。而当该企业被纳入碳排放权交易机制后，碳排放成本的内部化带来了企业总成本的上升。而碳排放权的市场价格越高，企业所承受的成本压力越大。此时，理性的企业可能会因此减少产品(电力)的生产，或者在碳市场中购买配额以覆盖其生产带来的碳排放。上述两种行为均会促使产品(电力)的供给曲线由S1左移至S2，从而使得市场均衡点变为M1。而由于传统能源(如电力)价格在多数国家遭受管制，市场新的均衡价格P1与实际电价P*间的差额只能发电企业自己承担。同时，随着碳约束的不断严格，企业获得的碳初始配额越来越少，碳配额的市场均衡价格不断走高，从而逼迫该企业继续减产或者转向投资新能源产业。

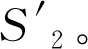
碳排放权交易市场与新能源市场的资产价格存在正向的相依关系。

具体而言，碳排放权交易价格的提升会通过增加新能源技术的需求而提升新能源公司股票的市场价格，而新能源公司产品价格的上升反过来又会通过迫使履约企业增加对排放配额的需求而带来碳排放权市场价格的上升。接下来将引入计量经济模型以更为深入地分析两者的正向相依结构。

二、 碳排放权交易市场与新能源市场资产价格相依性的计量经济分析

(一) 静态相依结构建模：基于二元Copula-GARCH模型

1. 基于Copula函数的联合分布

刻画碳排放权交易价格收益率(U)和新能源板块收益率(V)之间的二元Copula函数C是一个多元分布函数，其边缘分布是[0，1]区间的均匀分布。该二元Copula函数的严格定义为：若两大市场资产价格收益率序列均服从[0，1]区间的均匀分布，则随机向量(U,V)的联合分布为一个Copula函数，记为(U,V)～C。根据Sklar(1959)，该二元随机向量的联合分布函数F可被表示为

F(u,v)=C(FU(u),FV(v))

(1)

其中，FU、FV为(U,V)的边缘分布，C是描述(U,V)间相依结构的Copula函数。如果两个变量的累积分布函数可微，则(U,V)的联合密度f可表示为

f(u,v)=c(u,v)·FU(u)·FV(v)

(2)

由于建模过程中对边缘分布函数无需严格的要求和假设，Copula函数提供了一个有效构建二元或多元联合分布模型的方法：首先确定各变量的边缘分布，然后选择一个Copula函数来表示变量之间的关联结构，从而构造一个多元联合分布度量变量间的相依结构。

2. 二元Copula函数的分类

依据研究的需要而选取6类最为典型的Copula函数开展相关的分析，包括最为简单两类具有对称概率密度函数的Copula函数(Normal Copula函数和t-Copula函数)与三类常用的Archimedean Copula函数(Gumbel Copula函数、Clayton Copula函数和Frank Copula函数),以及目前运用较为普遍的SJC Copula函数。在这些Copula函数中，仅Normal Copula函数不能刻画变量间的尾部相依性特征，而在其他类Copula函数中，除t-Copula、Frank Copula函数外均可以刻画非对称的变量相依结构。SJC Copula函数是对原Joe-Clayton Copula函数的一个变形，能够有效地刻画变量在上尾和下尾间非对称的相依特征。上述6类Copula函数的基本特征详见表1所示。

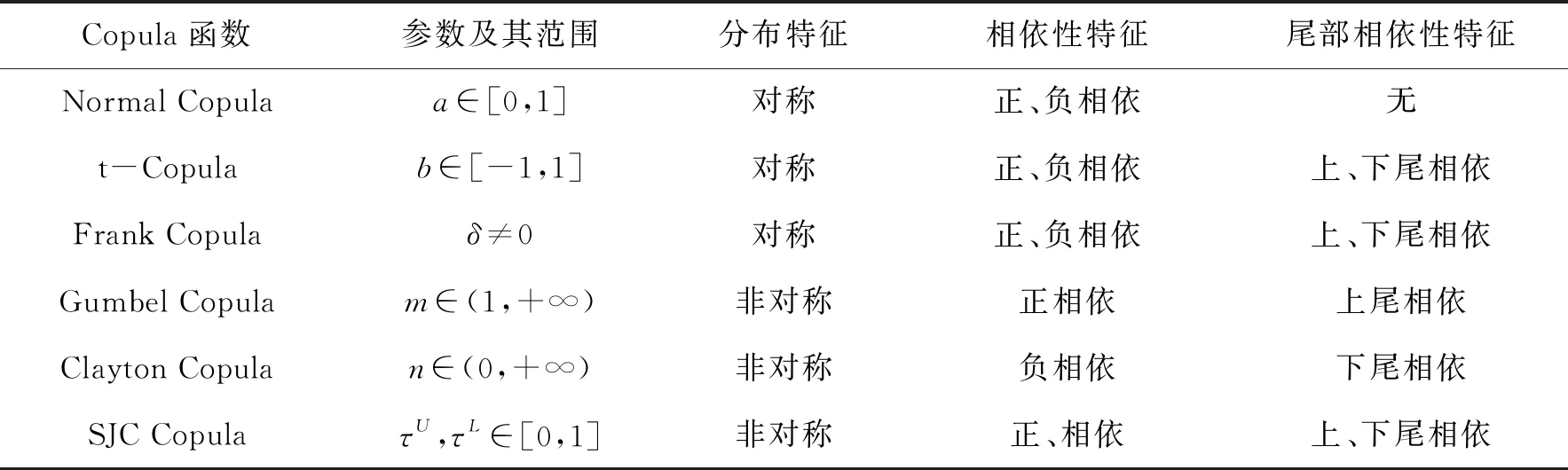
表1 采用的几类经典的Copula函数

3. 边缘分布建模

采用经典的广义自回归条件异方差(Generalized ARCH，GARCH)模型刻画排放权交易价格和新能源行业指数的波动特征，以描述碳排放权交易价格收益率和新能源板块收益率这两个随机变量的边缘分布。该模型的基本结构定义如下：

(3)

其中，{yt}为收益率序列，{ut}为相应的条件均值序列，而{εt}则为扰动项序列，t=1,…,N，N为样本个数。{ht}为{εt}的条件方差序列，{ξt}为独立同分布序列，且ξt与{εt-1,εt-2,…}相互独立。参数ω≥0，αi≥0，βj≥0，其中i=1,…,p，j=1,…,q，而ARCH项和GARCH项阶数p和q均不小于0。一般地，p和q的值可以依据AIC、BIC等准则确定得到。此时该模型被称为GARCH(p,q)。而如前所述，碳排放权交易价格和新能源行业指数不仅具有时变波动特性，还常呈现尖峰、厚尾、有偏的特征。因此，序列{ξt}除了被假设服从正态分布外，更多地被认为服从t分布、广义误差分布(GED)等。依据在{ξt}不同分布假设下的对数似然函数，采用极大似然估计的方法得到相关参数的估计值。

4. 二元Copula-GARCH模型的构建

采用GARCH模型分别刻画碳排放权交易价格的收益率序列{y1,t}和新能源行业指数的收益率序列{y2,t}，结合Copula理论可以得到二元Copula-GARCH模型：

(4)

其中，Ct(·,·)为任意的一个二元Copula函数，F1(·)和F2(·)可以表示标准正态分布、均值为0而方差为1的正规化t分布或正规化GED分布中的任意一种分布函数，ρt为该二元Copula函数的参数(依据不同的Copula函数类型给出不同的标识)。对于静态Copula函数，ρt为常参数，即ρt恒等于ρc。

(二) 动态相依结构建模：基于二元时变Copula-GARCH模型和DCC GARCH模型的比较

采用两种方法刻画碳排放权交易价格和新能源行业指数的动态相依结构，即二元时变Copula-GARCH模型和另一类常见的二元变量DCC-GRACH模型，在实证分析中将对二者的估计结果进行比较。

1. 二元时变Copula-GARCH模型

依据Patton(2006)，采用一个类似于ARMA-type过程来描述式(4)的第三个公式中的ρt，以刻画二元Copula-GARCH模型参数的时变特征。Patton(2006)、吴恒煜和胡根华(2014)等经典文献已给出上述多种经典Copula函数的时变参数，在此仅给出SJC Copula函数上、下尾时变参数的表达式，即

(5)

2. 二元变量DCC-GARCH模型

依据Engle(2002)的研究，尝试采用DCC-GARCH模型刻画碳排放权交易市场和新能源市场的动态相依结构。此时，假设碳排放权交易价格的收益率序列{y1,t}和新能源行业指数的收益率序列{y2,t}均服从均值为0、方差协方差矩阵为Ht的分布，即

yt|Ωt-1～N(0,Ht)Ht≡Dt·Rt·Dt

(6)

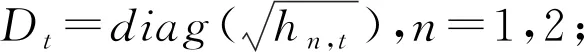
(7)

(三) 模型参数的估计方法概述

针对给出的静态Copula函数和时变Copula函数，均采用两阶段极大似然估计法对相关的参数加以估计，即首先对碳排放权交易价格和新能源行业指数序列的边缘分布加以估计，然后将相应的估计值作为已知数代入Copula函数中估计其参数。与静态Copula函数不同的是，在第二阶段估计时变Copula函数的参数时，需要将估计出的边缘分布参数以及时变相依参数和时变相关系数的动态模型代入相应的时变Copula函数中，得到时变相依参数和相关系数的极大似然估计值(谢赤等，2016)。

采用两阶段法估计二元变量DCC GARCH模型的参数，即首先估计单变量GARCH模型，然后根据所估计出的标准化残差来估计动态条件相关性的参数(Engle et al，2001)。

三、 实证分析

(一) 实证数据及描述性统计

本文选取我国深圳碳排放权交易试点市场配额的日现货价格和国证新能源指数的日收盘价作为样本，实证分析碳排放权交易市场与新能源市场间资产价格的相依关系。所选取的样本期是从2013年8月1日至2018年4月30日。样本数据均由Wind数据库并经整理(剔除其中的节假日和暂停交易日)后得到，共计1608组数据。

首先，对上述样本选取的合理性做简要说明。研究仅选取深圳碳排放权交易市场的配额现货价格是考虑到该市场在我国碳市场建设中的代表性：该地区相对市场化程度较高，而深圳碳排放权交易市场是我国首个启动的碳市场试点，配额交易日数据缺失较少，连续性相对较好，并且是首个成交额突破万亿的碳市场(郭文军，2015；胡根华等，2017)。而选取国证新能源指数(CNI NEW ENERGY INDEX，深交所代码：399412)来体现我国新能源行业的市场收益情况也是考虑到该指数在我国资本市场上的关注度和权威性。该指数不仅包括了Wind数据库所分类的在上海、深圳两大交易所上市的64家新能源公司，还涵盖了近年来国家大力支持的以新能源汽车为主的上市公司。因此，该指数也有较高的市场代表性，可以较好地反映新能源公司的经营状况。

其次，分析深圳碳排放交易价格和国证新能源指数的样本统计特征。得到两变量的对数收益率序列，分别简称为SZTJ和CNEI，在样本区间内的变化趋势如图3所示。表2给出了相应的描述性统计量。由图3可以初步判断两收益率序列具有一定的正向相依关系，与之前所提出的理论假设基本一致。而从表2可以看出，在样本期内，SZTJ序列相对CNEI序列而言均值较低但方差较大，体现出我国碳排放权交易市场还处于初期不成熟的阶段；而从两序列分别呈现出一定程度的右偏和左偏态也能看出类似的结论。同时，两序列均具有明显的尖峰后尾特点，不具备正态分布的特征；而ADF检验和Q统计量与LM统计量的检验结果均表明这两序列都为平稳时间序列且具有异方差性，从而采用GRACH模型刻画SZTJ和CNEI序列是合理的。

图3 深圳碳排放交易价格和国证新能源指数的收益率序列(SZTJ和CNEI)的变化趋势

表2 深圳碳排放交易价格和国证新能源指数的收益率序列(SZTJ和CNEI)的描述性统计量

(二) 静态相依结构分析

1. 边缘分布模型的确立

本文选取最合适的时间序列模型刻画SZTJ和CNEI序列的波动特征，以构建Copula-GRACH模型最优的边缘分布函数。首先，依据AIC、BIC准则和对数似然估计值(Log L)来确定刻画两序列波动的GARCH模型中ARCH项、GARCH项的滞后阶数和残差序列所服从的分布特征。而由表3所示，t-GARCH(1,1)模型是最优的。然后，表4给出的参数估计结果也显示两个t-GARCH(1,1)模型的参数均显著。最后，还通过K-S积分检验(见表5)，发现通过对两序列GARCH模型的残差项做积分变换后，新的时间序列服从独立同分布的均匀分布，从而进一步说明选取GARCH模型刻画Copula模型的边缘分布函数是合适的。

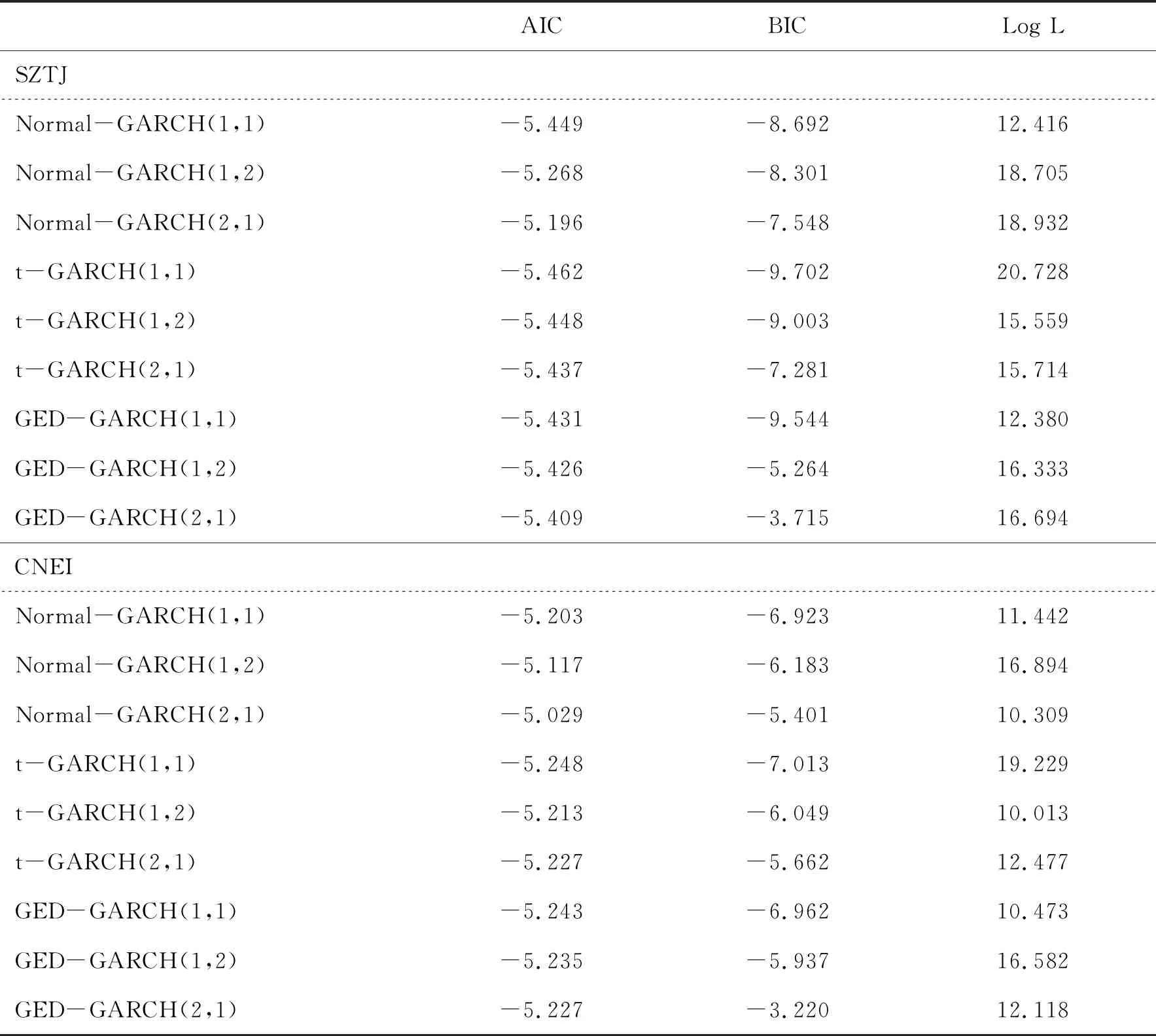
表3 深圳碳排放交易价格和国证新能源指数收益率序列(SZTJ和CNEI)的不同模型拟合效果检验

表4 深圳碳排放交易价格和国证新能源指数收益率序列(SZTJ和CNEI)t-GARCH(1,1)模型的参数估计

表5 深圳碳排放交易价格和国证新能源指数收益率序列(SZTJ和CNEI)概率积分的K-S检验

2. 二元静态Copula-GARCH模型的参数估计

研究选取静态Copula-GARCH模型捕捉碳排放权交易市场和新能源市场间资产价格的静态相依结构。由表6给出的参数估计结果，本文认为不论依据对数似然函数估计值还是AIC、BIC准则，选取SJC Copula函数刻画两序列的相依结构是最合适的。上述估计结果充分说明，碳排放权交易市场和新能源市场的资产价格存在非对称的相依结构，而两变量在上尾部的相关性显著增强。由此推断：当市场信息出现利好时，两市场的相依程度更高；而当市场状况不佳时，碳排放权交易市场和新能源市场资产价格的相关性明显减弱。

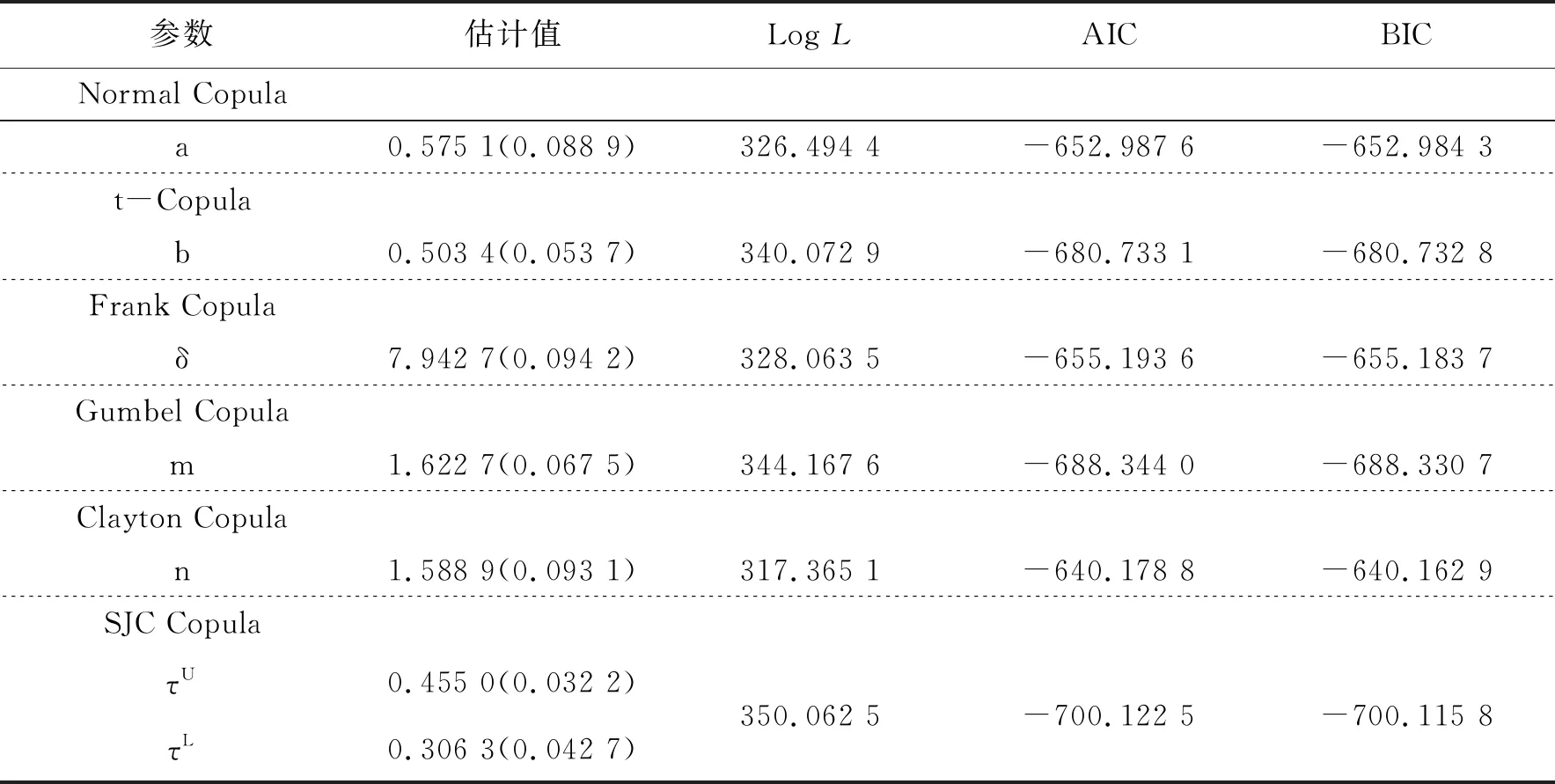
表6 静态Copula-GARCH模型的参数估计

(三) 动态相依结构分析

1. 二元时变Copula-GARCH模型的参数估计

依据静态Copula-GARH模型的估计结果，本文进一步分析碳排放权交易市场和新能源市场间资产价格的动态相依结构。为此，给出了在静态模型中拟合效果的t-Copula、Gumbel Copula和SJC Copula函数时变的相关参数(见表7)。表中给出的对数似然值和AIC、BIC准则的估计结果均表明：第一，时变Copula函数相对于静态模型更好地刻画了两变量的相依结构；第二，时变SJC Copula函数在刻画碳排放权交易市场和新能源市场间资产价格动态相依结构上是最佳的。通过观察时变SJC Copula函数上尾和下尾相关系数的变化(如图4所示)还发现：两时间序列在样本区间内始终具有正向的相关关系，而在上尾部二者的相关程度更高。这说明，当受到利好信息冲击时，碳排放权交易市场和新能源市场资产价格的联动性与协同性更强，可能会产生更大的波动溢出效应。

表7 时变Copula-GARCH模型的参数估计

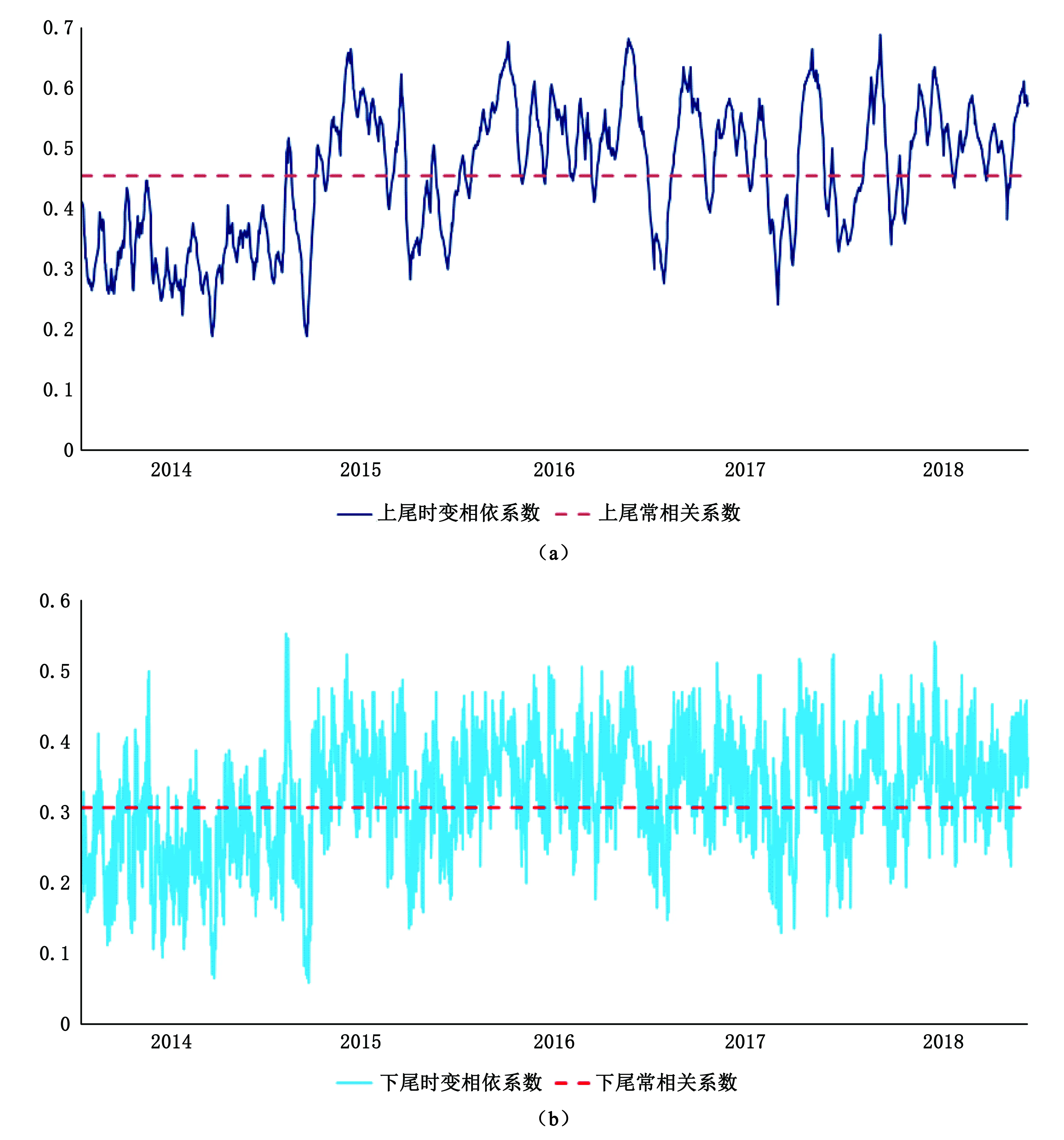
图4 基于时变SJC Copula模型的深圳碳排放交易价格和国证新能源指数收益率序列(SZTJ和CNEI)上尾部(a)和下尾部(b)的时变相关系数变化图

2. 二元变量DCC-GARCH模型的参数估计

运用二元变量t-DCC-GARCH(1,1)模型刻画碳排放权交易市场和新能源市场资产价格的动态波动相关特征。该模型的参数估计结果见表8，而相应得到的两变量动态相关系数的变化图如图5所示。可以看出，二元变量t-DCC-GARCH(1,1)模型在刻画两市场资产价格的动态相依特征上，结果是显著的。我们可以看出，两个模型均刻画出两市场正向的动态相依关系，同时两市场相依程度在碳排放权交易试点启动时波动较大而后期波幅收窄且呈现略有上升的特点。这一结果在印证之前所提出理论假设的同时，也反映出随着碳排放权交易机制的不断优化和新能源政策的逐步跟进，两市场的正向相依程度逐渐增强。

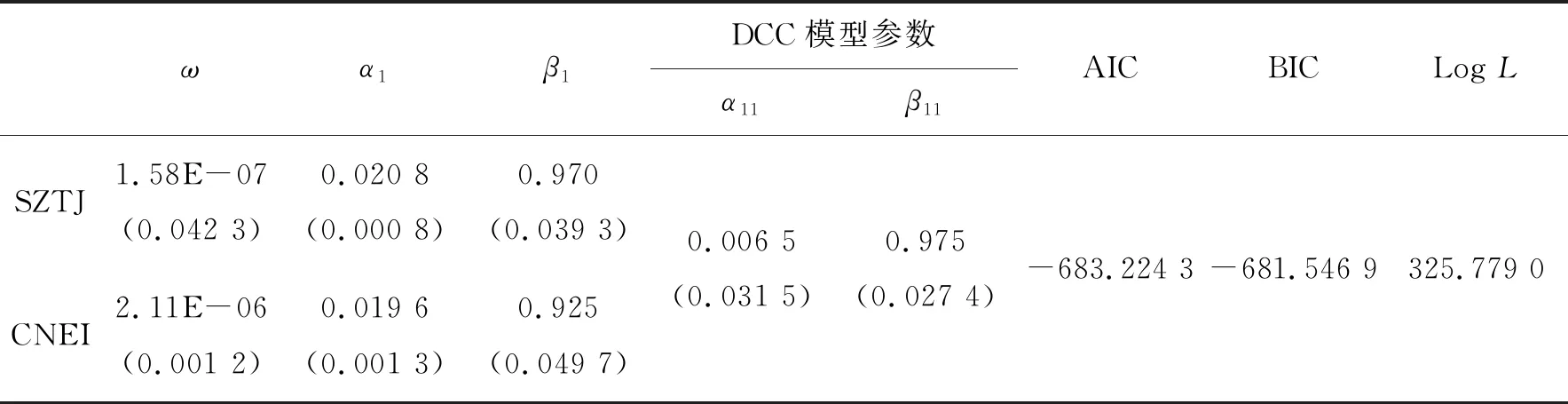
表8 二元变量t-DCC-GARCH(1,1)模型的参数估计

图5 基于DCC-GARCH模型的深圳碳排放交易价格和国证新能源指数收益率序列(SZTJ和CNEI)动态相关系数变化图

(四) 碳排放权交易市场与新能源市场间资产价格间波动的非对称动态相依结构分析

运用时变SIC Copula-GARCH模型,准确刻画了碳排放权交易市场与新能源市场间资产价格的正向相依关系，从而印证了依据市场供求模型分析所得出的理论假设；同时，该模型也刻画出两个市场存在非对称的动态相依结构。

从两市场非对称的动态相依结构看，在利好信息到来时，碳排放权交易市场和新能源市场的相依程度更高。这是因为两大市场均会显著受到国家政策直接驱动的影响。碳排放权交易机制是政策制定者为有效控制温室气体排放而人为构建的市场形态，碳排放权的稀缺性是由国家的减排政策导向直接带来的；而新能源产业目前仍然存在市场占有率低、投资成本高、市场风险较大的特点，其发展也离不开国家政策的有利扶持。因此，只有当政策制定者带来进一步大力减排、扶持新能源产业的利好消息时，投资者才愿意继续进行新能源技术的投资，并充分运用碳排放权交易这一市场机制为新能源产业的发展拓宽融资渠道。此时，投资者较高的市场预期带来了两大市场资产价格相依程度的明显增强。

从两市场相依程度的变化趋势看，随着碳排放权交易机制设计的不断深入，两市场的相依程度不断提高。在我国碳排放权交易机制试点启动伊始(2013—2014年)，国家对新能源产业的扶持力度不强，投资者对国家减排政策仍多维持观望态度，因此两市场的相关性较弱且波动较大。而当其他排放权交易试点悉数启动(2014年)后，国家运用市场化减排手段控制温室气体排放的政策导向日趋明朗,《碳排放权交易管理暂行办法》《中美元首气候变化联合声明》《关于切实做好全国碳排放权交易市场启动重点工作的通知》等相关政策文本的出台为我国统一碳市场的建设勾画了基础框架，而《全国碳排放权交易市场建设方案(发电行业)》在2017年底的印发标志着我国统一碳市场的正式启动。此时，我国新能源行业体现出国家政策日趋完善、市场竞争日渐激烈的特点。我国在“十三五”期间有关新能源各类行业的发展规划悉数出台，同时风力、光伏等行业产能过剩的问题逐步缓解，新能源市场在国家政策的扶持下逐渐完善。上述有关控制温室气体排放和发展新能源产业的国家政策为两大市场带来了诸多利好信息，从而使得两市场的相依程度明显增强并表出现更为稳定的特点。

四、 结论与政策建议

我国在“十三五”规划期间大力推进碳排放权交易机制建设的同时，也出台一系列政策集中解决新能源补贴资金扩大、消纳能力不足等问题(涂强等，2020)。而这两大政策的有效实施势必会对新能源公司的发展带来“利好信息”。因此，运用经济学理论刻画与分析碳排放权交易机制与新能源产业政策间的协调关系，对于有效促进我国节能减排目标的实现至关重要。

本文尝试运用计量经济模型来揭示碳排放权交易市场与新能源市场资产价格间的相关结构，以对上述议题加以解读。本文首先通过分析在市场化减排背景下传统能源市场与新能源市场均衡的变化，提出有关碳市场与新能源市场资产价格“存在正向相依关系”的理论假设。然后，建立Copula-GARCH模型和DCC-GARCH模型刻画两大市场资本价格动态相依结构。通过采用我国深圳试点地区碳排放权市场现货价格和国证新能源指数开展的实证分析发现：能够捕捉尾部风险的t-GARCH(1,1)模型较好地刻画两大市场资产价格的波动特征，而运用能够刻画上下尾部非对称相依特征的SJC Copula函数的实证结果印证了理论假设，也捕捉到两大市场非对称的波动影响结构。同时，本文运用时变Copula模型和DCC-GARCH模型刻画出碳市场与新能源市场的非对称的正向动态相依模式。

实证分析部分所发现的碳市场与新能源市场资产价格间逐步上升且日渐稳定，揭示我国近年来减排政策与新能源产业政策间的协调与相互影响：随着碳排放权交易机制的逐步完善和新能源政策的不断推进，碳排放权交易市场和新能源市场间的相依程度不断增强并渐趋稳定。此时，投资者将有意识地关注碳排放权的市场价格信息以调整投资策略，针对新能源市场做出更为理性的投资决策，为新能源产业的发展带来更为积极而理性的市场资本的支持。因此，政策制定者在未来不断推动和完善碳排放权交易机制的建设时，要注重减排机制和新能源政策间的协调性，关注碳市场和新能源市场间资产价格的联动关系，充分发挥碳排放权交易市场的价格发现功能,以有力引导新能源产业的投资行为，从而保证节能减排与社会低碳转型目标的实现。

研究还存在一定的不足，需要在未来的分析中加以完善。在研究方法上：第一，构建更为完善的微观经济学模型以更好地分析碳排放权交易市场和新能源市场间的相依关系；第二，不论是Copula函数还是刻画时变波动特征的GARCH模型，目前均有更多已改进的模型方法可用以更好地刻画市场间的相依模式。在研究视角上：第一，在研究的基础上可以分析构建碳排放权交易市场和新能源市场间的风险组合，采用VaR模型等技术以更好捕捉两大市场价格的协同性；第二，将传统能源行业、高耗能行业等其他相关市场的资本价格信息引入研究中，在丰富研究内容的同时，可以更好地实证分析碳排放权交易机制在推动传统能源行业和高耗能行业转型以及新能源行业发展上的作用，为碳排放权交易机制的设计与完善提供更多的理论依据。