纳米流体中纳米颗粒分散性能的分子动力学模拟

生丽莎 陈振乾,2

(1东南大学能源与环境学院, 南京 210096)(2东南大学江苏省太阳能技术重点实验室, 南京 210096)

纳米流体是一种二元组分固-液混合物，是在给定流体(水、醇、油等)中掺入超细金属或非金属/金属氧化物颗粒形成的一种胶体悬浮液[1].与常规流体相比，纳米流体具有良好的导电、导热性能、流动性及摩擦减阻性质，因此在强化传热传质[2-6]、能量储存[7-8]、机械应用[9-11]、生物医药[12-15]、燃料电池等多个领域具有广泛的应用.

稳定性是限制纳米流体进一步广泛应用的重要因素.纳米颗粒的聚集与纳米流体的制备、使用及整体设备的损耗都密切相关.Derjaguin-Landau-Verwey-Overbeek(DLVO)理论认为，当颗粒以布朗运动相互接近时，纳米流体的稳定性取决于范德华力和静电力的总和[16-18].在稳定的纳米流体或胶体中，排斥力起着主导作用.影响胶体稳定性的排斥力主要有静电排斥力和空间位阻2种类型.

国内外学者们主要通过实验研究来分析纳米流体的分散稳定性.纳米流体的稳定性评估方法包括Zeta 电势分析法[19]、沉淀法[20]、离心法[21]、光谱分析法[22]、3ω法[23]以及电子显微镜和光散射法[24].其中沉淀法是评价纳米流体稳定性的最基础方法，它通过施加外力场使纳米颗粒沉淀并通过上清液纳米颗粒的浓度来判定纳米颗粒的稳定性.当上清液纳米颗粒浓度随时间维持恒定时，可认为纳米颗粒保持分散稳定.

目前，已有学者通过分子动力学方法对纳米流体的热导率、黏度等传递性质及强化传热机制进行了大量的研究工作[25]，但关于纳米流体分散稳定机理方面的研究却很少.崔文政等[26]建立了以水分子为基础液、Cu纳米颗粒为悬浮粒子的纳米流体模型，模拟结果表明纳米颗粒在基础液中进行高速随机旋转和平移运动.Bao等[27]建立了以Ar为基础液体、Cu为悬浮粒子的纳米流体模型，研究结果表明，大尺寸纳米颗粒对应的纳米流体具有较小的黏度，纳米颗粒聚集增大了纳米流体的运动速度；相对于纳米颗粒尺寸，纳米颗粒聚集对纳米颗粒的黏度影响较大.Lu等[28]建立了以水为基础液体、TiO2为悬浮粒子的纳米流体模型，模拟结果表明，纳米颗粒在水溶液中的聚集受尺寸影响；强表面相互作用和高表面扩散系数导致小尺寸纳米颗粒表面间形成键结构；水分子介导作用在纳米颗粒聚集过程中起到重要作用.Sheng等[29]建立了大孔径中空SiO2基多孔液体表面模型，模拟结果表明外冠聚合物刷可有效阻隔中空SiO2核，从而阻止纳米颗粒聚集，形成稳定多孔液体.

分子动力学方法能够提供纳米尺度流动和传递现象的精确模拟.基于此，本文构建以水为基础液、中空SiO2纳米颗粒为悬浮粒子的纳米流体模型，采用分子动力学模拟的方法计算纳米颗粒表面间距离、相互作用能、径向分布函数及颗粒表面水扩散系数等参数，从而分析考察SiO2纳米颗粒的运动过程及聚集微观机理.

1 模型和方法

1.1 建立模型

为考察中空SiO2纳米颗粒在流体中的运动特性，建立以水为基础液的纳米流体模型(见图1).盒子尺寸为11 nm × 11 nm × 11 nm，中心放入2个内、外径分别为2和4 nm、质心距离为5 nm的中空SiO2纳米颗粒，其余区域分散着40 150个水分子.通过截取SiO2超晶胞获得中空SiO2纳米颗粒，其内外表面O和Si原子断裂的键分别通过H和O原子进行饱和，连接有3个羟基的Si原子被删去.

图1 水基纳米流体系统的初始构型

1.2 模拟设置

本文采用LAMMPS软件进行计算[30].模拟在压力101 kPa、温度300 K条件下进行.模拟系统采用周期性边界条件，粒子初始速度服从高斯分布，模拟时间步长为2 fs，LJ(Lennard-Jones)势能截断半径为1.5 nm，静电势能截断半径设置为1.2 nm，采用 PPPM(particle-particle particle-mesh)方法处理粒子间的长程静电相互作用.水分子的键长键角采用SHAKE算法固定.分子动力学计算采用NVT正则系综，采用Nose-Hoover热浴法控制体系温度，为消除系统中的不合理相互作用，首先采用Polak-Ribiere算法对整个模拟进行能量最小化.总模拟时长为3.5 ns.

1.3 模拟参数及方法

本文采用LJ的12-6势能Uvdw描述纳米颗粒间非键相互作用，Coulombic势能Ucoul描述纳米颗粒间非静电相互作用.水分子采用SPC/E势能模型，SiO2纳米颗粒势能参数如表1所示[31-32].表中，σ、ε为LJ势能参数,q为原子电荷，e为元电荷.原子间总相互作用能U计算公式如下：

(1)

式中，εij和σij为LJ势能参数；C为能量转换因子；κ为介电常数；qi、qj分别为原子i、j的电荷；rij为原子对间的距离.不同原子间LJ势能参数采用如下混合法则：

(2)

(3)

分子间相互作用可用表面相互作用能Eint表示，定义如下[33]：

Eint=Etot-(Enl+Enr)

(4)

式中，Etot为总能量，kJ/mol；Enl和Enr分别为左、右纳米颗粒的能量，kJ/mol.能量绝对值的大小反映分子间相互作用的强弱，绝对值越大说明相互作用越强烈.

流体扩散系数D通过均方位移(MSD)计算得到，计算公式如下：

(5)

式中，rk(t)为分子k在t时刻的位置；N为系统原子总数目.

2 结果与讨论

2.1 聚集过程

通过计算中空SiO2纳米颗粒质心距离的变化来描述颗粒的聚集过程.由图2(a)可知，纳米颗粒运动过程可分为2个阶段：黏结阶段和平衡阶段.在0～0.04 ns内，纳米颗粒迅速相互靠近，纳米颗粒质心距离由5.00 nm 缩减到4.04 nm；随后，纳米颗粒质心距离在4.04～4.21 nm范围内波动.由图2(b)可知，纳米流体中纳米颗粒的运动可分为3个阶段：布朗运动阶段、黏结阶段、平衡阶段.初始阶段(0～0.3 ns)，纳米颗粒质心距离为5.00 nm，距离较远，纳米颗粒在水中进行无规则运动，即布朗运动；随后(0.3～0.9 ns)，纳米颗粒质心距离逐渐减小，纳米颗粒运动到彼此附近并发生聚集现象；发生团聚后，纳米颗粒在距离4.11～4.19 nm范围内波动.结果表明，纳米流体中流体介质可有效减缓纳米颗粒的聚集速度；纯纳米颗粒和纳米流体中的纳米颗粒一旦发生聚集，均将无法自行分散[34].

(a) 纯纳米颗粒

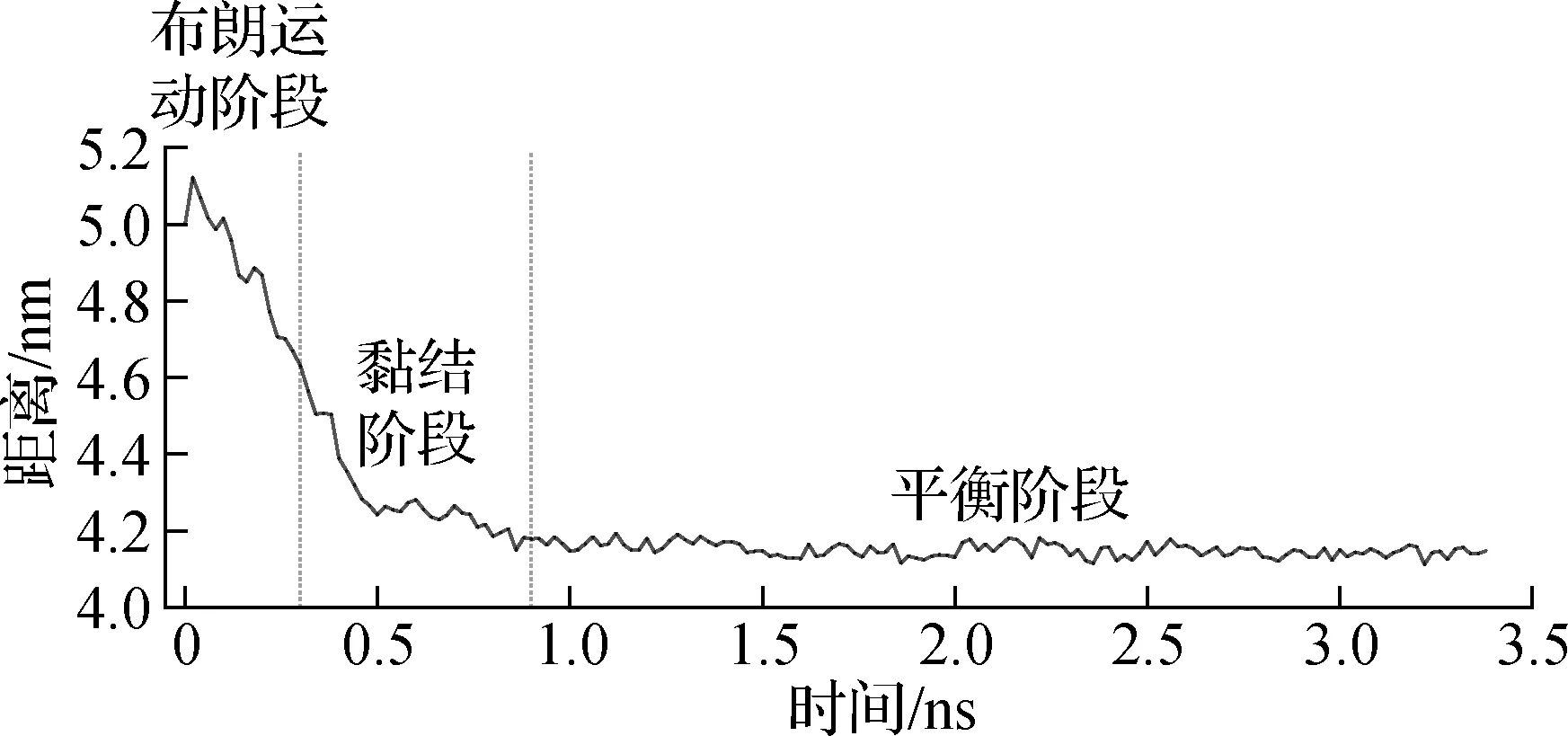
(b) 纳米流体中纳米颗粒

2.2 运动构象

纳米颗粒运动构象如图3所示.由图可知，纳米颗粒均在黏结阶段后聚集在一起，但平衡阶段聚集形态各有差异，为表述清晰，将初始构型中左右2个纳米颗粒分别标记为A、B.在0.04～2.6 ns内，2个纯纳米颗粒同时发生转动，纳米颗粒A运动到纳米颗粒B上方；在2.6～5.0 ns内，纳米颗粒继续转动，纳米颗粒A运动到纳米颗粒B右侧.而纳米流体中纳米颗粒在平衡阶段聚集在一起，不存在转动过程.这是因为水分子会阻碍纳米颗粒相互靠近，包括转动过程.下面从相互作用能和水分子扩散系数2个方面探讨水分子对纳米颗粒聚集产生的影响.

2.3 相互作用能

为研究纳米颗粒在水中的聚集机理，计算纯纳米颗粒及纳米流体中纳米颗粒间的相互作用能.当相互作用能为正值时，纳米颗粒之间表现为相互排斥；当相互作用能为负值时，纳米颗粒之间表现为相互吸引.由图4(a)可知，纯纳米颗粒相互作用能在正负之间剧烈震荡，这可能是由于纳米颗粒距离太近而导致纳米颗粒间产生强烈的排斥及吸引作用.由图4(b)可知，纳米颗粒相互作用能变化与运动情况一致.在布朗运动阶段，纳米颗粒间距离较远，颗粒相互作用能忽略不计，此时纳米颗粒在水中进行无规则运动；当纳米颗粒运动到彼此附近时，分子间作用能增大，导致纳米颗粒进一步相互靠近，相互作用能从-38 kJ/mol增加到-632 kJ/mol；当纳米颗粒发生团聚时，总相互作用能在-632 kJ/mol 上下波动，纳米颗粒间通过范德华力相互吸引，纳米颗粒间距离在4.11～4.19 nm范围内波动.

(a) 0 ns(纯纳米颗粒)

(e) 3.3 ns(纯纳米颗粒)

(i) 0.18 ns(纳米流体)

(a) 纯纳米颗粒

(b) 纳米流体中的纳米颗粒

氢键作用理论认为氢键是导致纳米颗粒硬团聚的重要原因[35].本文通过径向分布函数(RDF)图讨论纳米流体中的氢键作用.图5为纳米流体中中空SiO2纳米颗粒与周围水分子的RDF图，图中g(r)表示中空SiO2纳米颗粒表面羟基上氢氧原子(Hso、Oso)周围水分子氢氧原子(Hw、Ow)沿径向区域密度随距离r的变化情况.由图可知，纳米颗粒表面H原子与水分子中的O原子形成的RDF曲线(g(r)Hso-Ow)的峰值出现在0.307 5 nm处，说明H、O原子间形成氢键[36]；纳米颗粒表面O原子与水分子中的H原子形成的RDF曲线(g(r)Oso-Hw)分别在0.217 5和0.367 5 nm处出现峰值，其中第1个峰值验证了氢键的存在，第2个峰值超出氢键的范围.因此，纳米颗粒可与表面水分子形成较强的氢键相互作用，使得水分子黏附在纳米颗粒表面，阻碍纳米颗粒相互靠近，延缓纳米颗粒聚集.

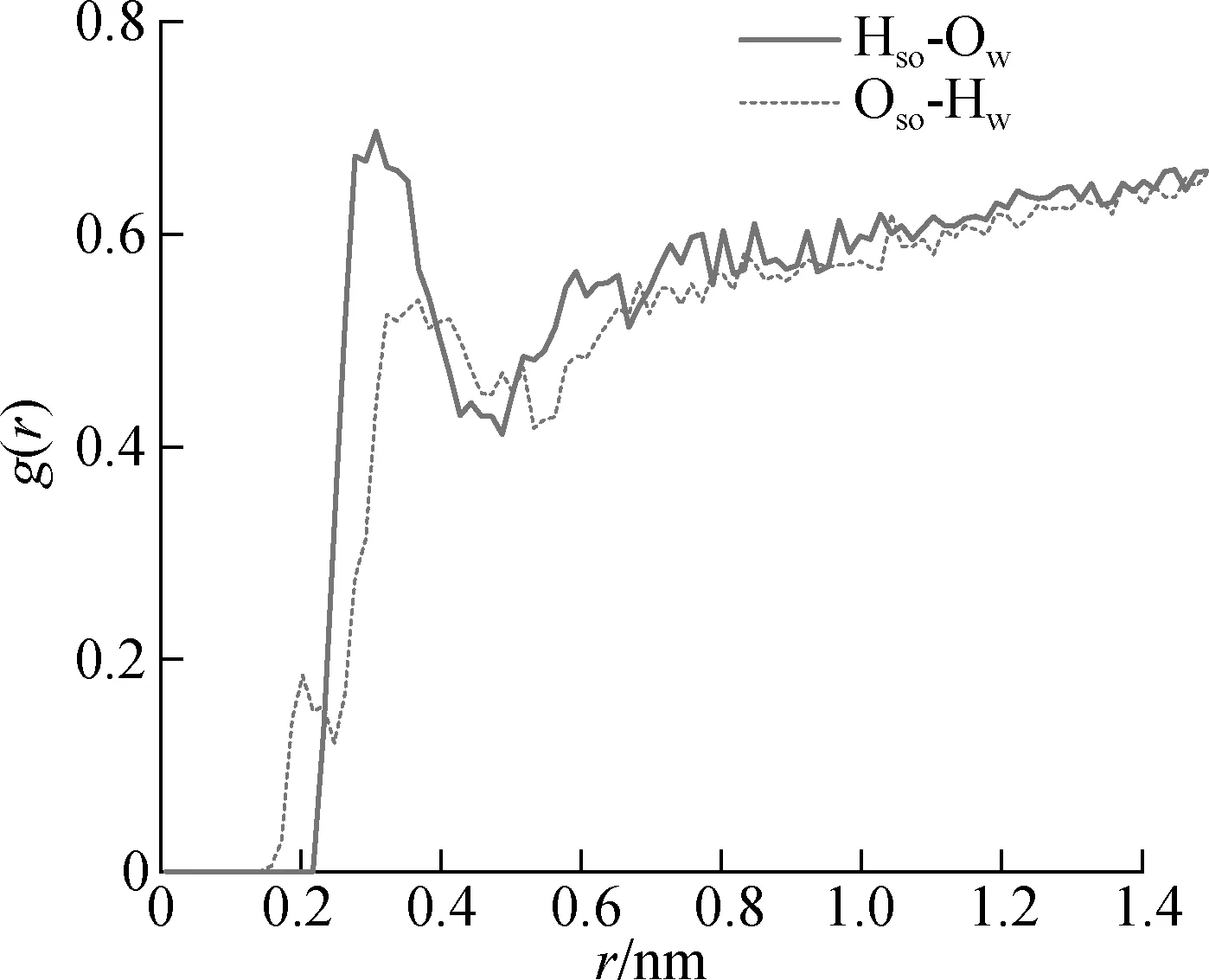
图5 中空SiO2表面羟基上氢氧原子周围水分子氢氧原子的径向分布函数

2.4 扩散系数

图6为800 ps时纳米颗粒表面不同距离水分子的扩散系数.由图可知，当水分子与纳米颗粒表面距离为0.3和0.6 nm时，水分子扩散系数分别为1.29 × 10-11、4.43 × 10-11m2/s，此时水分子扩散系数较小，水分子黏附在纳米颗粒表面，形成纳米颗粒间的隔断；当水分子与纳米颗粒表面距离为0.9、1.2、1.5和1.8 nm时，水分子扩散系数分别为 1.47 × 10-9、2.01 × 10-9、2.29 × 10-9和2.43 × 10-9m2/s，水分子扩散系数随颗粒间距离增大而增大，流动性增强.因此，纳米颗粒间距离表面越远的水分子更容易被挤出.随着纳米颗粒的相互靠近，水分子由于氢键作用而黏附在纳米颗粒表面，阻隔作用越明显，纳米颗粒相互靠近速度越慢，这与2.1节中结果一致.

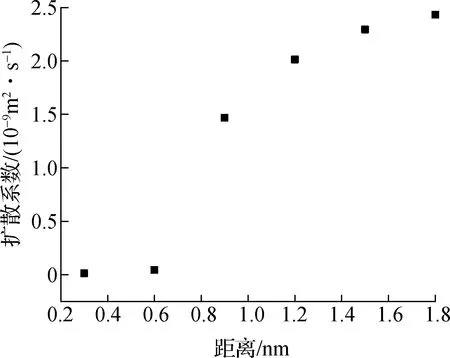
图6 纳米颗粒表面水分子的扩散系数

3 结论

1) 采用分子动力学模拟方法，利用LAMMPS软件，从全原子角度考察中空SiO2纳米颗粒的运动特性，结果表明:纯纳米颗粒极易发生团聚；纳米流体中纳米颗粒首先做无规则热运动，随着颗粒间距离减小，纳米颗粒运动到彼此附近并发生团聚现象.一旦发生团聚，纳米颗粒均不能自行分散开.

2) 纳米颗粒间相互作用是长程范德华力与静电力之和，其变化与颗粒间距离紧密相关.纯纳米颗粒由于距离太近会产生强烈的排斥及吸引作用，相互作用能在正负之间剧烈震荡；纳米流体做无规则热运动时，颗粒间距离较远，相互作用能接近于零；随着纳米颗粒相互靠近，相互作用能逐渐增大；当纳米颗粒发生团聚时，纳米颗粒间表现为吸引力，相互作用能随颗粒间距离在-632 kJ/mol上下波动.

3) 纳米颗粒表面与水分子之间形成的氢键使水分子紧密黏附在纳米颗粒表面，阻止纳米颗粒相互靠近，延缓纳米颗粒相互聚集.

4) 距离纳米颗粒表面较近的水分子扩散系数接近于零；随着距离的增大，水分子扩散系数增大至2.43 × 10-9m2/s.这意味着距离纳米颗粒表面越远的水分子越容易从纳米颗粒之间排挤出来，因此纳米颗粒在运动初期靠近速度较快，随着纳米颗粒间距离的缩短其靠近速度变慢.